次元の呪いの真の範囲を可視化する

Visualizing the true extent of the curse of dimensions.

モンテカルロ法を使用して、非常に多くの特徴を持つ観測の振る舞いを可視化する

データセットを考えてみてください。それはいくつかの観測からなり、各観測にはN個の特徴があります。すべての特徴を数値表現に変換した場合、各観測はN次元空間上の点と言えます。

Nが低い場合、点の間の関係は直感的に予想できるものです。しかし、Nが非常に大きくなることがあります。たとえば、ワンホットエンコーディングなどで多くの特徴を作成する場合などです。Nが非常に大きい場合、観測はまるで疎なものとして振る舞ったり、距離が予想よりも大きくなったりするかのように見えます。

この現象は実際に起こります。次元数Nが増え、他の要素が変わらない場合、観測を含むN次元の体積は実際に増加します（少なくとも自由度の数が増える）、そして観測間のユークリッド距離も増加します。実際に点のグループはより疎になります。これが次元の呪いの幾何学的な基礎です。データセットに適用されるモデルや技術の振る舞いは、これらの変化の結果として影響を受けるでしょう。

特徴の数が非常に大きい場合、さまざまな問題が発生する可能性があります。観測よりも特徴が多い状況は、過学習の典型的な設定です。そのような空間でのブルートフォース検索（例：グリッドサーチ）は効率が低下します。任意の軸に沿って同じ間隔をカバーするには、より多くの試行が必要です。距離や近傍に基づいたモデルに微妙な影響があります。次元の数が非常に大きくなると、観測の任意の点を考慮すると、他のすべての点が遠く、いくらか均等距離に見えるようになります。これらのモデルは距離に依存して仕事を行うため、距離の差が均等化されることで、彼らの仕事がより困難になります。たとえば、クラスタリングは、すべての点がほぼ等距離に見える場合にはうまく機能しません。

• AIの進歩を促進するための医療データのラベリングをゲーム化する
• データサイエンスにおけるキャリアキャピタルを構築するために非常に過小評価されている方法
• トップ3のデータアーキテクチャのトレンド（およびLLMsがそれらに与える影響）

これらの理由やその他の理由から、PCA、LDAなどの技術が開発されました。非常に多くの次元を持つ空間の特異な幾何学から離れ、実際に含まれている情報により適した次元数にデータセットを縮約するためのものです。

直感的にこの現象の真の大きさを理解するのは難しいですし、3次元を超える空間は非常に視覚化が困難です。したがって、直感を助けるためにいくつかのシンプルな2Dの視覚化を行いましょう。次元数が問題になる理由には幾何学的な基礎があり、これをここで可視化します。これまで見たことがない場合、結果は驚くかもしれません。高次元空間の幾何学は、典型的な直感が示唆するよりもはるかに複雑です。

体積

原点を中心としたサイズ1の正方形を考えます。その正方形に円を内接させます。

これが2次元の設定です。次に、一般的なN次元の場合を考えます。3次元の場合、立方体に内接する球があります。それ以上の次元では、N次元の立方体に内接するN次元球があります。単純化のため、これらのオブジェクトを「球」と「立方体」と呼びます。次元数に関係なくです。

立方体の体積は一定で、常に1です。問題は、次元数Nが変化すると、球の体積はどうなるかです。

モンテカルロ法を使用して実験的にこの質問に答えましょう。大量の点を生成し、立方体内で均等かつランダムに分布させます。各点の原点からの距離を計算し、その距離が0.5未満（球の半径）であれば、その点は球の内部にあります。

球の内部にある点の数を総点数で割ると、球の体積と立方体の体積の比率が近似されます。立方体の体積は1なので、この比率は球の体積に等しいことになります。総点数が大きいほど、近似度は向上します。

言い換えると、inside_points / total_pointsの比率は、球の体積に近似します。

このコードは非常にシンプルです。多くの点を必要とするため、明示的なループは避ける必要があります。NumPyを使用することもできますが、CPUのみでシングルスレッドのため、遅くなります。代替手段としては、CuPy（GPU）、Jax（CPUまたはGPU）、PyTorch（CPUまたはGPU）などがあります。ここではPyTorchを使用しますが、NumPyコードはほぼ同じになります。

入れ子になったtorchのステートメントに従っていくと、100億個のランダムな点を生成し、原点からの距離を計算し、球の内部にある点の数を数え、その数を総点数で割ります。 ratio配列には、異なる次元の球の体積が格納されます。

調整可能なパラメータは、24 GBのメモリを持つGPUに設定されていますので、ハードウェアが異なる場合は調整してください。

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")# CPUを強制的に使用する場合# device = 'cpu'# ratioの値が0.0になる数が多すぎる場合は、d_maxを減らすd_max = 22# メモリが不足する場合は、nを減らすn = 10**8ratio = np.zeros(d_max)for d in tqdm(range(d_max, 0, -1)):    torch.manual_seed(0)    # メモリ割り当てを改善するため、大きなテンソルステートメントを組み合わせる    ratio[d - 1] = (        torch.sum(            torch.sqrt(                torch.sum(torch.pow(torch.rand((n, d), device=device) - 0.5, 2), dim=1)            )            <= 0.5        ).item()        / n    )# メモリを解放torch.cuda.empty_cache()

結果を可視化しましょう:

N=1の場合は自明です。 “球”と”キューブ”は線分であり、等しいので、”球”の”体積”は1です。 N=2およびN=3の場合は、高校の幾何学の結果を覚えておく必要があり、このシミュレーションが非常に正確な値に非常に近いことに気付くでしょう。

Nが増えるにつれて、非常に劇的なことが起こります。球の体積は急速に減少します。N=10の時点で0に近づき、N=20前後でこのシミュレーションの浮動小数点精度を下回ります。その後、コードは球の体積を0.0と計算します（これは近似値です）。

>>> print(list(ratio))[1.0, 0.78548005, 0.52364381, 0.30841056, 0.16450286, 0.08075666, 0.03688062, 0.015852, 0.00645304, 0.00249584, 0.00092725, 0.00032921, 0.00011305, 3.766e-05, 1.14e-05, 3.29e-06, 9.9e-07, 2.8e-07, 8e-08, 3e-08, 2e-08, 0.0]

Nが大きい場合、ほとんどのキューブの体積は角にあります。球を含む中央領域は比較において無視できるくらい小さくなります。高次元空間では、角が非常に重要になります。ほとんどの体積は角に”移動”します。Nが上昇すると、これが非常に速く起こります。

別の見方をすると、球は原点の”近辺”です。Nが増えると、点はその近辺から単に消えてしまいます。原点はそれほど特別ではないので、その近辺に起こることは、どこでもすべての近辺に起こるはずです。”近辺”という概念自体が大きく変わります。Nの上昇に伴い、近所は空になります。

このシミュレーションを初めて実行したのは数年前で、球の体積がNの上昇に伴い0に急速にダイブする様子を鮮明に覚えています。コードをチェックしてもエラーは見つからず、私の反応は次のようでした：作業を保存し、画面をロックし、外に出て散歩し、見たことについて考えてみてください。:)

直線距離

まずは、Nを関数として立方体の対角線の長さを計算しましょう。これは非常に簡単で、対角線の長さは文字通りsqrt(N)なので、コードも非常にシンプルです。以下に結果を示します。

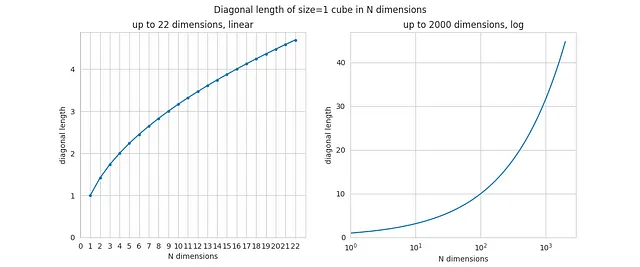
N=2やN=3の場合は、幾何学的な結果（正方形や通常の3次元立方体の対角線）として認識できるはずです。しかし、Nが増えるにつれて対角線も増加し、その成長は無限です。

これは非常に直感に反するかもしれませんが、立方体の辺のサイズが一定（つまり1である）ままでも、Nを増やすと対角線の長さは任意の大きさになります。N=1000の場合、対角線の長さは約32です。理論的には、立方体の辺の長さが1メートルであれば、対角線の長さが1キロメートルになる空間が非常に多くの次元で存在することになります！

辺に沿った距離は同じままでも、次元の数に比例して対角線は増加し続けます。

新しい次元が空間に追加されるたびに、エッジや面などが存在するようになり、コーナー領域の構成はより複雑になり、自由度が増えます。その結果、対角線の長さも少し長くなります。

観測間の距離

では、観測点やポイント間の距離はどうでしょうか？ある固定数のランダムな点を生成し、任意の2点間の平均距離と任意の点の最近傍点への平均距離を計算します。すべての点は常に立方体に含まれます。Nが増えると、平均距離にはどのような影響があるでしょうか？別のシミュレーションを実行してみましょう。

メモリ管理については保守的なアプローチを採用していることに注意してください。使用されているデータ構造は非常に大きいため、重要です。

n_points_d = 10**3# どのようなポイントの組み合わせがあるかを示す変数dist_count = n_points_d * (n_points_d - 1) / 2# 距離のペアワイズ行列を使用するため、各距離は2回数えられるdist_count = 2 * dist_countd_max = d_max_diagavg_dist = np.zeros(d_max)avg_dist_nn = np.zeros(d_max)for d in tqdm(range(d_max, 0, -1)):    torch.manual_seed(0)    # ランダムなポイントを生成    point_coordinates = torch.rand((n_points_d, d), device=device)    # すべての軸のポイント座標の差分を計算    coord_diffs = point_coordinates.unsqueeze(1) - point_coordinates    del point_coordinates    # 座標の差分を二乗する    diffs_squared = torch.pow(coord_diffs, 2)    del coord_diffs    # 2点間の距離を計算    distances_full = torch.sqrt(torch.sum(diffs_squared, dim=2))    del diffs_squared    # ポイント間の平均距離を計算    avg_dist[d - 1] = torch.sum(distances_full).item() / dist_count    # 最近傍点までの距離を計算    distances_full[distances_full == 0.0] = np.sqrt(d) + 1    distances_nn, _ = torch.min(distances_full, dim=0)    del distances_full    # 最近傍点までの平均距離を計算    avg_dist_nn[d - 1] = torch.mean(distances_nn).item()    del distances_nntorch.cuda.empty_cache()

ここではポイント数をはるかに少なくしています（たったの1000個）が、メインのデータ構造のサイズはN^2に比例するため、ポイントを生成しすぎるとすぐにメモリが不足します。それでも、おおよその結果は実際の値に十分近いはずです。

以下は、Nに関数として1000個のポイントの任意の2点間の平均距離です：

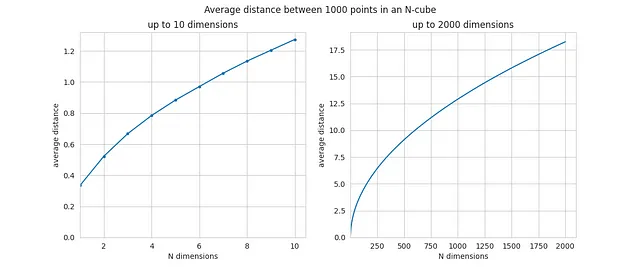
Nの値が小さい場合、平均距離は0.5や1のような値になります。しかし、Nが増えると平均距離も増加し、N=2000の時点で既に18に近づいています。増加は著しいです。

これはNに関数としての最も近い隣人への平均距離です：

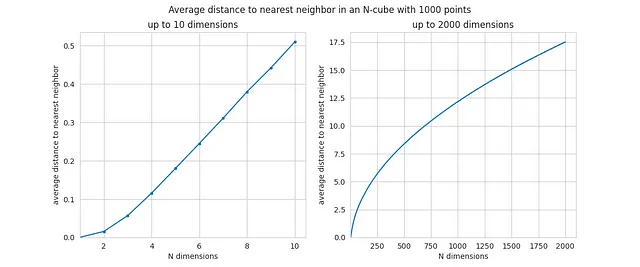
ここでの増加はさらに劇的であり、Nが10未満の場合は値が非常に小さく、点が低次元空間で密集しています。 Nの値が大きくなると、最も近い隣人への平均距離は実際には任意の2点間の平均距離に非常に近くなります-言い換えれば、周囲の空間の空虚さが測定を支配します。

これが高次元空間では「点がほぼ等距離になる」と言った理由です-平均距離と最短距離はほぼ同じになります。ここにシミュレーションからの証拠と現象の強さに対する直感があります。

次元数Nが増加すると、すべての点がお互いから遠ざかりますが、座標は同じ狭い範囲（-0.5、+0.5）に制約されています。単により多くの次元を作成することで、点のグループは効果的にますます疎になります。次元が数単位から数千単位に増加すると、増加は数桁にわたります。非常に大きな増加です。

結論

次元の呪いは実際の現象です。他のすべてが同じであれば、次元（または特徴）の数を増やすと、点（または観測値）は迅速に離れていきます。実質的には、線形間隔を沿った軸に沿って同じですが、内部にはより多くの余地があります。すべての近傍は空になり、各点は高次元空間で孤立しています。

これにより、いくつかの手法（クラスタリング、さまざまなモデルなど）が特徴の数が大幅に変化すると異なる動作をすることの直感が提供されるはずです。少数の観測値と多数の特徴が組み合わさると、最適な結果が得られない場合があります-次元の呪いはその理由の一つですが、唯一の理由ではありません。

一般的には、観測値の数は特徴の数に「追いつく」必要があります-ここでの正確なルールは多くの要因に依存します。

それ以外の場合でも、この記事は高次元空間の特性についての直感的な概要を提供するはずであり、それは視覚化が困難なものです。いくつかの傾向は驚くほど強力であり、これでその強さをある程度理解することができるはずです。

この記事で使用されたすべてのコードはこちらです：

misc/curse_dimensionality_article/n_sphere.ipynb at master · FlorinAndrei/misc

random stuff. Contribute to FlorinAndrei/misc development by creating an account on GitHub.

github.com

この記事で使用されたすべての画像は著者によって作成されました（上記のコードリンクを参照）。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!