「VIFを超えて バイアス軽減と予測精度のための多重共線性分析」
VIFを超えた共線性分析
機械学習において、共線性は経験豊富なプロフェッショナルから初心者までの複雑な問題です。機械学習(ML)アルゴリズムは、予測の正確さを最適化することに最適化されており、ターゲットの予測子の説明可能性ではありません。また、共線性に対処するためのほとんどの解決策、例えば「分散膨張スコア(Variance Inflation Score)」や「ピアソンの相互相関分析(Pearson’s cross-correlation analysis)」などは、前処理において大量の情報損失を引き起こす可能性があります。
ほとんどの機械学習アルゴリズムは、予測の正確さを最適化するために最適な組み合わせの特徴量を選択します。そのため、共線性があっても、トレーニングで観察される相関が現実世界でも真実である限り、機械学習においては問題ではありません。ただし、モデルの説明可能性において、共線性の未チェックの影響はバイアスの潜在的な原因となります。

共線性とは、データセット内の独立変数(IVs)間の高い相関を指します。これは、回帰モデルの解釈において独自の課題を提供することが多く、データ内の関係の真の理由を特定するのを妨げ、バイアスのある解釈や不公平な意思決定につながることがあります。たとえば、図1では、独立変数(TAX)、(B)、(RAD)は共線性のあるIVであり、また依存変数(MEDV)の良い予測子でもあります。MLアルゴリズムは最適な予測子の組み合わせを選択しますが、これらの3つの変数のいずれかを持つモデルにさらに共線性のある変数(RM)を追加する効果を考慮することができない場合があります。
共線性の分析を前処理のステップとして真剣に取り組むよう機械学習者に促すためには、共線性変数の総膨張コストと削除の予測コストをバランスさせる方法が必要です。
- 「雨は雨を予測するのか?米国の気象データと今日と明日の雨の相関関係」
- 「ナレッジグラフを必要とする理由と、それを構築する方法」
- Pythonコード生成のためのLlama-2 7Bモデルのファインチューニング
共線性の理解
未チェックの共線性が意図しないバイアスにつながる方法を示すために、「データ収集の方法」という警告の例として「ボストンの住宅データセット」を使用してみましょう。このデータセットは後に論破され、一般の使用から撤回されました。なぜなら、データセットには「B」という「非可逆」変数が含まれているからです。独立変数「B」、「RM」、「TAX」の間の共線性の関係は、見かけの相関がIV間の真の関係を抑制する典型的なケーススタディです。「B」に対する「非可逆」変換(連続的なIVを連続的でないバイナリIVとして偽装する)は、MLアルゴリズムで検出されない調整バイアスを導入する可能性があります。

ボストンの住宅データセットには、所有者が居住する住宅の中央値(MEDV)が依存変数(DV)として、13の独立変数(IVs)があります。特定の特徴は結果の強力な予測子に見えるかもしれませんが、それらの影響は他の予測子によって大部分が説明されている分散によるものです。

独立変数と従属変数の間の2変量関係では、新たな独立変数が導入された場合、以下の4つの可能性があります:
- 偽の膨張:第3のIVの追加により、最初のIVがDVに対する影響が大幅に増大します。
- マスキングまたは抑制:新しいIVは、初期のIVと従属変数への影響を隠したり抑制したりします。
- 調整または変更:新しい変数は、独立変数のすべてまたは一部の観測において元の関係の方向を変えます。
- 何も影響しない:第3のIVは新しい情報を提供せず、独立変数および従属変数に影響を与えません。
機械学習者にとって、既製の共線性の解決策はしばしば予測力の低下、過学習モデル、そしてバイアスを引き起こす結果となります。したがって、情報の損失を軽減する解決策が重要です。
共線性の評価
2つ以上の独立変数が高い相関を示している場合(RADとTAX)、共線性の背後にある直感は、それらが依存変数(物件価値)に対するある「潜在的な」概念(ビッグサバーブハウス/シティアパートメント)の影響に関してまったく同じ情報を提供する可能性があるということです。”Property Tax”の存在下で、径路高速道路へのアクセスは物件価値に新たな情報を提供しない(またはその逆)。意味のない高い相関がある場合、回帰モデルの係数は大きくなり、結果に対するいくつかの要因の効果に関する推論が過大評価されます。
現在、共線性に対処する方法は2つありますが、どちらも依存変数を考慮していません。
- ペアワイズ相関:いくつの独立変数が互いに「強く」相関しているか。相関係数の「強く相関している」特徴のカットオフは主観的ですが、一般的な合意では相関係数が+/- 0.7のときに共線性が深刻な問題となります。
def dropMultiCorrelated(cormat, threshold): ##Define threshold to remove pairs of features with #correlation coefficient greater than 0.7 or -0.7 threshold = 0.7 # Select upper triangle of correlation matrix upper = cormat.abs().where(np.triu(np.ones(cormat.shape), k=1).astype(np.bool)) # Find index of feature columns with correlation greater than threshold to_drop = [column for column in upper.columns if any(upper[column] > threshold)] for d in to_drop: print("Dropping {}....".format(d)) return to_drop2. 分散膨張:相関係数は2つの独立変数の対応する変化の程度を確認しますが、それは独立変数の重要性についてはほとんど教えてくれません。これは、多変量関係において、独立変数は依存変数に対して真に独立して影響を持っていないためです(図1を参照)。そして、その影響の真の有意性は他の独立変数の組み合わせの存在下で見られます。
分散膨張スコアは、独立変数の係数に他の独立変数への依存性によって追加される影響の大きさです。VIFは、IVを1つずつ外した状態を依存変数とし、残りの内部変数を独立変数として扱います。つまり、すべてのIVが依存変数になり、各モデルが(R2)値を生成します。このR2値は、外した状態のIVの分散の割合を内側のIVが説明していることを示します。VIFスコアは次のように推定されます:
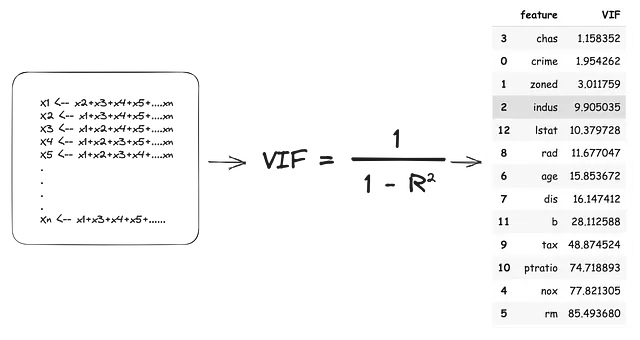
上記のVIF推定に従って、共線性を完全に解決するためには13のIVのうち11を削除する必要があります。これは大量の情報の損失だけでなく、現実世界で性能の低い過学習モデルを生み出す可能性もあります。
機械学習では、ペアワイズの多重相関やVIFスコアだけが特徴の破棄または保持の唯一の基準ではありません。
一部の特徴は、高い相関やVIFスコアにもかかわらず、重要な予測値を提供したり、モデルの解釈に貢献したりする場合があります。
共線性に対する膨張コストと予測コストの比較
情報の損失を軽減するために、共線性のある特徴を保持することの膨張コストと、それらを削除することの予測コストを比較することができます。VIF分析はアウトカム変数とは独立して行われるため、個々のIVの独立な影響を完全に考慮していません。
## 複数の線形回帰モデルを構築して、結果に対する真の独立影響を評価する
fs = []
for feature in X_train.columns:
model = sm.OLS(Y_train, sm.add_constant(X_train[feature])).fit()
fs.append((feature, model.params[feature]/model.pvalues[feature]))
## 値を抽出して保存する
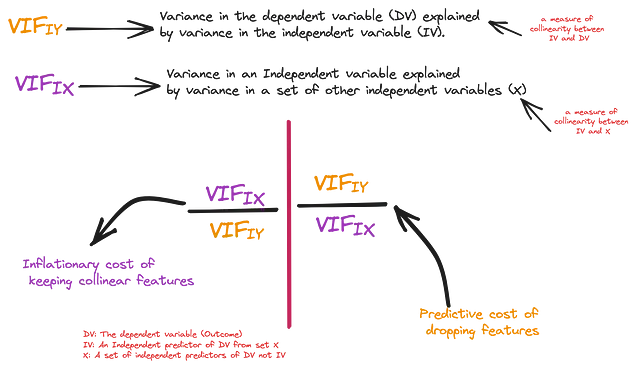
c1 = pd.DataFrame(coefs, columns=['Feature', 'VarianceEx']).sort_values("VarianceEx")最初の測定値は、独立変数(IV)が従属変数に与える影響、つまり従属変数の分散量、IV(R_squared)によって独立して説明される量です。一貫性のために、このR_squared値からVIFスコアを推定し、これをVIF(IY)と呼びます-独立重要度。二つ目の測定値は、全てのIVが存在する場合の独立変数が従属変数に与える影響、つまり上記で推定されたVIFです。これをVIF(IX)と呼びます-集合的重要度。
これで、相関のある特徴量を削除することによって失われる「驚き」の本当の量を自信を持って推定することができます。以下のグラフでは、X軸は各IVが説明するYの分散(予測の「有用性」の尺度)、Y軸は他のIVによって説明されるIVの分散(モデルへの「バイアス」の尺度)を表します。サブプロット1のバブルのサイズは、これらの変数をモデルに保持することによるインフレーションコストで、サブプロット2のバブルのサイズはこれらの変数を削除することによる予測コストです。
これは前処理のステップなので、VIF(IX)のカットオフ値を20(赤線)およびVIF(IY)のカットオフ値を1.15(青線)として非常に寛大なものにします。したがって、赤い線の下にある特徴量は他のIVによって最も説明されておらず、青い線の後ろにある特徴量は(Y)を独立して予測することができません。
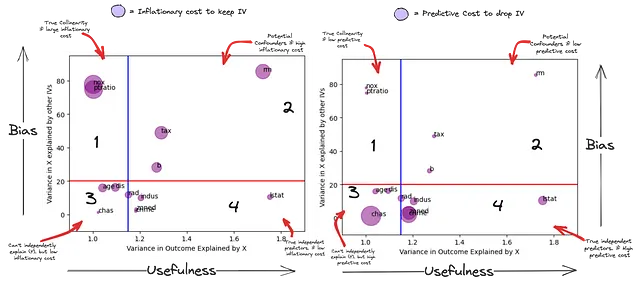
このグラフは、IVの独立予測力とバイアスの潜在的な関係を要約しています。
- 第1象限-潜在的に真の共線性:これらの特徴量(NOX、PTRATIO)は、モデル内のいくつかのIVの線形組み合わせで説明され、従属変数を独立して予測することはできません(有用になるためには他の一部のIVに依存する可能性があります)。さらに、彼らの持つ予測力は他のIVの線形組み合わせによって相殺される可能性があります(サブプロット2)。彼らの影響は他のIVの追加によって大幅に抑制されています。
- 第2象限-潜在的なバイアス:これらは従属変数と他の独立変数と関連しています。特徴量(RM、TAX、B)は(Y)を独立して予測する可能性がありますが、その分散は他の独立変数の組み合わせによっても説明されています。彼らのいわゆる独立予測力は、他の(IVs)との組み合わせなしでは解釈することができません。これらは、結果への意義を解釈する際に、アウトカムへの重要性を非常に高くするか、バイアスの源になる可能性があります。
- 第3象限-従属変数:これらは(Y)を独立して予測することはありませんが、一部の特徴量を削除することには高い予測コストがかかります。これは、他のIVによって説明されないユニークな情報を持っているためです。この「ユニークな」情報の有用性は、他のIV(s)との組み合わせでのみ考慮することができます。
- 第4象限-真の独立予測子:これらの変数は(Y)を独立して予測することができます。これらの変数は他のIVによって説明されないユニークな情報も持っています(第3象限よりも多く)。この「ユニークな」情報の有用性は、他のIV(s)とは独立して予測することができます。ただし、他のIVの線形組み合わせの方が独立予測よりも高い予測力を持つ場合があります。
O = Y_train# 特徴量Cの追加/削除が独立変数Iと結果Oの関係に与える効果を推定するためにconf = []for I in X_train.columns: # IがOに与える影響についてのベースラインモデルを構築する model = sm.OLS(O, sm.add_constant(X_train[I])).fit() IO_coef, IO_sig = model.params[I], model.pvalues[I] ## Cの影響をアクセスする for C in X_train.columns: if C != I: # IとOの関係にCを追加した補助モデルを構築する model2 = sm.OLS(O, sm.add_constant(X_train[[I, C]])).fit() ico_preds = model2.predict() ICO_coef, ICO_sig = model2.params[I], model2.pvalues[I] # CがOに与える影響についてのベースラインモデルを構築する model3 = sm.OLS(O, sm.add_constant(X_train[C])).fit() CO_coef, CO_sig = model3.params[C], model3.pvalues[C] corr_IC, _ = pearsonr(X_train[I], X_train[C]) # 独立変数対制御変数の相関 corr_IO, _ = pearsonr(X_train[I], O) # 独立変数対結果の相関 corr_CO, _ = pearsonr(X_train[C], O) # 制御変数対結果の相関 conf.append({"I_C":f"{I}_{C}", "IO_coef":IO_coef, "IO_sig":IO_sig, "CO_coef":CO_coef, "CO_sig":CO_sig, "ICO_sig":ICO_sig, "ICO_coef": ICO_coef, "corr_IC":corr_IC, "corr_IO":corr_IO, "corr_CO":corr_CO})cc = pd.DataFrame(conf)corr_ic = (cc['corr_IC'] > 0.5) | (cc['corr_IC'] < -0.5) # IとCは相関しているcorr_co = (cc['corr_CO'] > 0.5) | (cc['corr_CO'] < -0.5) # CとOは相関しているcorr_io = (cc['corr_IO'] > 0.5) | (cc['corr_IO'] < -0.5) # IとOは相関している## CとOは有意に相関しているco_sig = (cc['CO_sig'] < 0.01) # CはOを独立して予測しているio_sig = (cc['IO_sig'] <変数B、TAX、およびRMは互いに予測し、また独立して結果を予測します。これは、DV(MEDV)を最も良く予測するIVの線形組み合わせかもしれません。また、これらのIVのうち任意の2つの予測関連性は、第3のIVの存在によって膨張または抑制される可能性があります。これを調査するために、各変数はすべての独立変数からなるベースラインモデルから順次削除されるべきです。
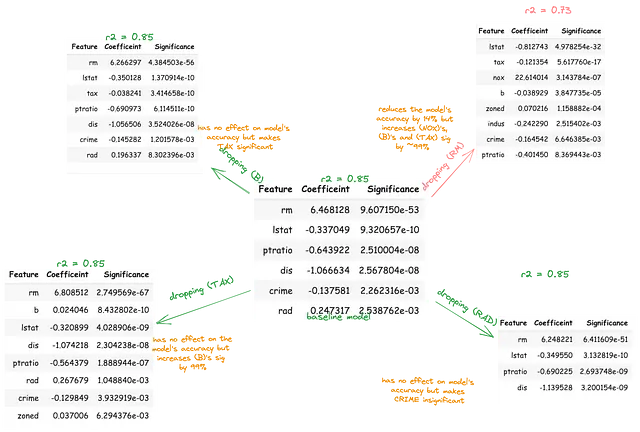
その後、残りの変数が結果に与える影響の対応する変化をパーセンテージで定量化する必要があります。この手順により、他のIVによって説明されるIVが重要であるかのように見せかけることができます。
赤線より上、共線性バイアスの削除
赤線より上の共線変数が他のIVと従属変数との関係に与える主な影響は、中介(抑制)、交絡(誇張)、または修正(変更)の3つです。
モデレータ、中介変数、および交絡変数の概念は、機械学習では実際にはあまり議論されていません。これらの概念は通常「社会科学者」に委ねられます。なぜなら、彼らは自分たちの係数を「解釈」する必要があるからです。ただし、これらの概念は、共線性がMLモデルにバイアスを導入する方法を説明します。
これらの効果は、より深い因果関係分析なしでは真に確立することはできませんが、バイアス除去の前処理手順として、これらの関係をフィルタリングするためにこれらの概念の単純な定義を使用できます。
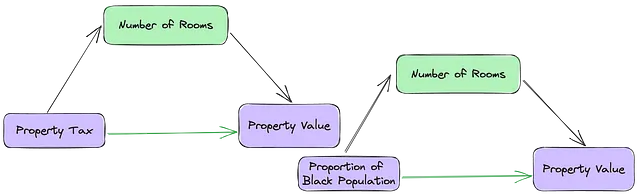
中介変数は、IVとDVの関係、つまりそれらが関連するプロセスを「どのように」説明します。中介変数は以下の3つの基準を満たす必要があります:
a)第1のIVの予測に有意であること、b)従属変数の予測に有意であること、およびc)第1のIVの存在下で従属変数の予測に有意であること。
中介変数は「中介的」であり、その含有は第1のIVと従属変数の関係の方向を変えません。中介変数がモデルから削除されると、第1のIVと従属変数の関係の強さが増すはずです。なぜなら、中介変数はその効果の一部を正当に説明していたからです。
## 中介変数の検索cc = pd.DataFrame(conf)co_sig = (cc['CO_sig'] < 0.01) # CはYを予測するio_sig = (cc['IO_sig'] < 0.01) # IはYを予測するic_oi_sig = (cc['ICO_I_sig'] < 0.01) # IとCはYを予測するic_oc_sig = (cc['ICO_C_sig'] < 0.05) # CはIの存在下でYを予測するic_oi_sig = (cc['IO_sig'] > cc['ICO_I_sig']) # IとOの直接的な関係はCなしの方が強いはず
例えば、(RM)、(TAX)、および(MEDV)の関係では、部屋の数は不動産税がその不動産価値と関連している方法を説明する可能性があります。
交絡変数は、相関と有意性の観点で定義するのが困難であるため、曖昧です。交絡変数は、従属変数と独立変数の両方と相関する外部変数であり、それらの関係を歪める可能性があります。中介変数とは異なり、第1のIVと従属変数の関係は無意味です。交絡変数を削除すると、第1のIVと従属変数の関係が弱まるか強まるかは保証されません。
家の部屋数は、黒人の割合と不動産価値の関係を中介または交絡する可能性があります。この論文によれば、(B)と(RM)の関係によります。もし(RM <-> MEDV)と(RM <-> B)の関係が同じ方向であれば、(RM)を削除すると(B)の(MEDV)への影響が弱まるはずです。ただし、(RM <-> MEDV)と(RM <-> B)の関係が逆方向であれば、(RM)を削除すると(B)が強まります。
(RM <—> MEDV) と (RM <-> B) は同じ方向にあります(図1のサブプロット3)。しかし、(RM) を除去すると (B) の効果が強まります。
しかし、下の図を見ると、第一の独立変数と従属変数の関係において、第三の独立変数には良い決定境界があります。これは、(RM) と (TAX) の間の異なる関係を示しており、(B) の値に基づいています。
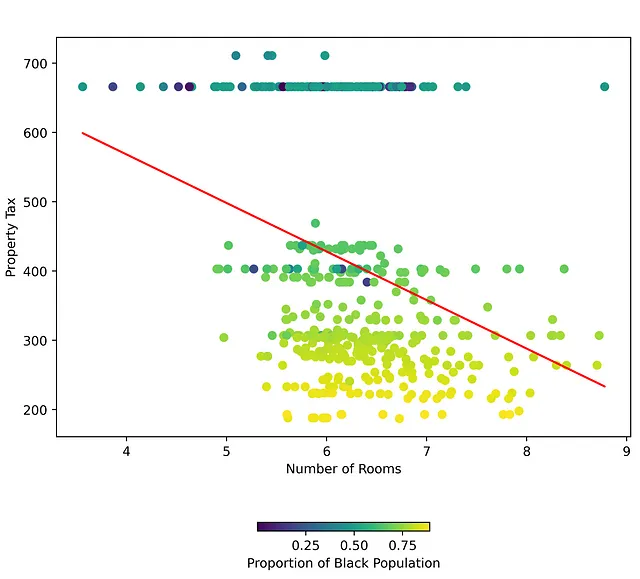
モデレーターを用いると、第一の独立変数と従属変数の関係はモデレーターの値に基づいて異なります。$100,000の家にかかる固定資産税はどれくらい予想できるでしょうか?実際、その町の黒人人口の比率とその家の部屋数に依存します。実際、(B) がある閾値以下であれば、部屋数に関係なく一定の固定資産税を持つ町の集合が存在します。
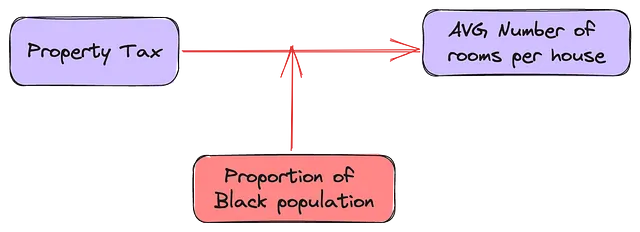
モデレーターは通常、データ内のカテゴリ特徴量やグループです。グループの場合、従属変数に対するモデレーション効果を考慮するために、各グループラベルのダミー変数を作成することが一般的です。ただし、ランク付けされた変数や分散が低い連続変数 (B) もモデレーターになり得ます。
結論
まとめると、共線性は回帰モデリングにおける難しい問題ですが、その注意深い評価と管理により、機械学習モデルの予測力と信頼性を向上させることができます。情報の損失を考慮する能力は、説明性と予測精度のバランスを可能にし、特徴選択の効果的なフレームワークを提供します。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
