「強化学習を使用してLeetcodeの問題を解決する」

Using reinforcement learning to solve Leetcode problems.

強化学習の実践的な導入

最近、leetcodeで質問を見つけました：障害物の除去を伴うグリッド内の最短経路。障害物の除去を伴うグリッド内の最短経路問題は、障害物が含まれる2Dグリッド内の開始セルから目標セルまでの最短経路を見つけることを目的としています。この経路に沿って最大でk個の障害物を除去することが許可されています。グリッドは「m x n」の0（空のセル）と1（障害物セル）の2D配列で表されます。

目標は、開始セル(0, 0)から目標セル(m-1, n-1)までの最短経路を見つけることであり、空のセルを通過しながら最大でk個の障害物を除去することです。障害物を除去するとは、障害物セル（1）を空のセル（0）に変換して、経路を通過できるようにすることを意味します。

この問題を解くにあたって、実際には強化学習の原理を理解するための有用なフレームワークを提供できることに気付きました。それに入る前に、この問題が従来どのように解決されているかを見てみましょう。

理想的には、開始セルからグラフ探索を行い、これまでに除去された障害物の数を追跡する必要があります。各ステップでは、隣接する空のセルに移動するか、隣接する障害物セルを除去するかを考慮します（除去の余地がある場合）。最短経路は、最も少ないステップ数で目標に到達し、最大でk個の障害物を除去する経路です。最適な最短経路を効率的に見つけるために、幅優先探索や深さ優先探索を使用できます。

• 「データモデリングのための一般人向けガイド ― 第2部：次元モデリングの基礎」
• インクから洞察：ブックショップの分析を使用してSQLとPythonのクエリを比較する
• 「物理データを使用してコンピュータビジョンを再焦点化する」

この問題のためのBFSアプローチを使用したPythonの関数は次のとおりです：

class Solution:    def shortestPath(self, grid: List[List[int]], k: int) -> int:        rows, cols = len(grid), len(grid[0])        target = (rows - 1, cols - 1)        # もし最悪の場合に障害物を除去するための十分なクオータがあれば、最短距離はマンハッタン距離です        if k >= rows + cols - 2:            return rows + cols - 2        # (行、列、障害物を除去する残りのクオータ)        state = (0, 0, k)        # (ステップ数、状態)        queue = deque([(0, state)])        seen = set([state])        while queue:            steps, (row, col, k) = queue.popleft()            # 目標に到達した場合はここで終了            if (row, col) == target:                return steps            # 次のステップで四方向を探索する            for new_row, new_col in [(row, col + 1), (row + 1, col), (row, col - 1), (row - 1, col)]:                # (new_row, new_col)がグリッドの範囲内にある場合                if (0 <= new_row < rows) and (0 <= new_col < cols):                    new_eliminations = k - grid[new_row][new_col]                    new_state = (new_row, new_col, new_eliminations)                    # 追加する次の移動が条件を満たしている場合はキューに追加                    if new_eliminations >= 0 and new_state not in seen:                        seen.add(new_state)                        queue.append((steps + 1, new_state))        # 目標に到達しなかった場合        return -1

強化学習の基礎

強化学習（RL）は、機械学習の分野の一部であり、エージェントが環境について学習し、報酬メカニズムを通じて方策を学習してタスクを達成するものです。私は常に強化学習に魅了されてきました。なぜなら、このフレームワークが人間が経験を通じて学習する方法に非常に近いからです。アイデアは、問題を解決するために環境について学習するための学習可能なエージェントを構築することです。

以下では、これらのトピックを項目ごとに詳しく見ていきましょう：

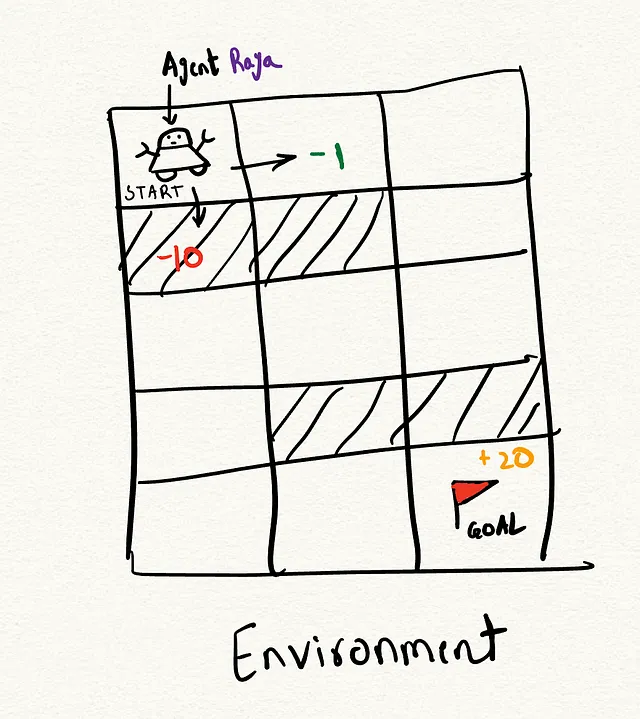
• エージェント：エージェントは行動の進行を制御する仮想的な実体です。仮想のロボット、エージェントラヤと想像してみてください。ラヤは位置からスタートし、環境を探索します。例えば、ラヤには2つのオプションがあります：右に進む位置（0, 0）または下に進む位置（0, 1）で、それぞれ異なる報酬があります。
• 環境：環境はエージェントが操作するコンテキストであり、この場合は2次元のグリッドです。
• 状態：状態はプレーヤーの現在の状況を表します。この場合、プレーヤーの現在の位置と残りの違反の数を示します。
• 報酬システム：報酬は特定の行動を取ることによって得られるスコアです。この場合、空のセルに対して-1ポイント、目的地に到達するために+20ポイント、違反の数kが尽きた場合には-10ポイントです。

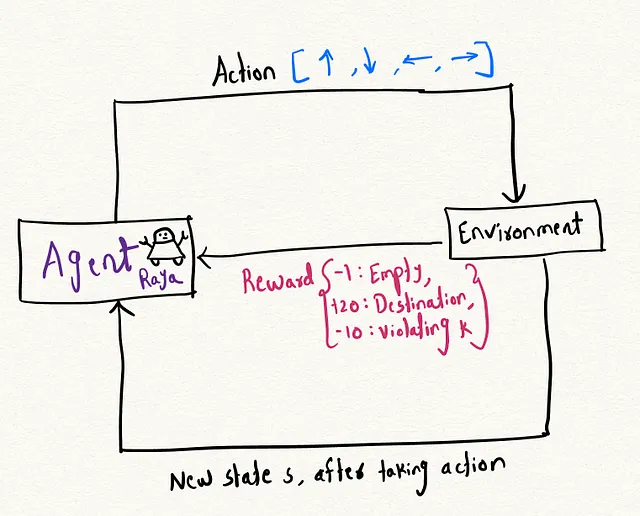
イテレーションのプロセスを通じて、我々は最適な方策を学習し、各時間ステップで最適な行動を見つけることができるようになります。また、総報酬も最大化されます。

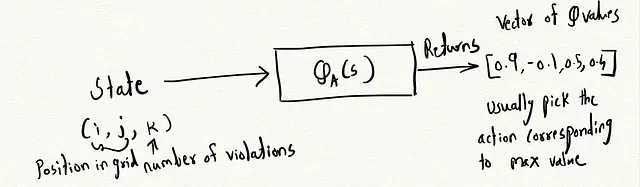
最適な方策を見つけるために、私たちはQ関数と呼ばれるものを使用しました。この関数は、エージェントがこれまでに行ったすべての探索の情報を保持するリポジトリと考えることができます。エージェントはこの履歴情報を使って、将来の報酬を最大化するより良い決定を行います。

Q関数

Q(s, a)は、方策πに従って状態sで行動aを取ることによってエージェントが達成できる期待累積報酬を表します。

ここで

• π：エージェントが採用する方策。
• s：現在の状態。
• a：エージェントが状態sで取った行動。

γは探索と活用のバランスを取る割引率です。これはエージェントが即時の報酬と将来の報酬にどれだけ優先度を付けるかを決定します。0に近い因子はエージェントが短期的な報酬に焦点を当てることを意味し、1に近い因子は長期的な報酬に焦点を当てることを意味します。

エージェントは既知の高報酬行動の活用と、より高い報酬が得られる可能性のある未知の行動の探索をバランスさせる必要があります。0から1の間の割引率を使用することで、エージェントが局所的に最適な方策に固執するのを防ぎます。

それでは、全体の動作のコードに移りましょう。

これがエージェントとそれに関連する変数の定義方法です。

報酬関数：報酬関数は現在の状態を受け取り、その状態で得られる報酬を返します。

ベルマン方程式：

どのようにしてQテーブルを更新すれば、各位置と行動に対して最適な値を持つことができるでしょうか？任意のイテレーションのために、エージェントは位置（0, 0, k）で開始します。ここでkは許容される違反の数を示します。各時間ステップで、エージェントはランダムに探索するか、学習済みのQ値を利用して貪欲に移動することによって新しい状態に移行します。

新しい状態に到達すると、即時の報酬を評価し、ベルマン方程式に基づいてその状態-行動ペアのQ値を更新します。これにより、各状態-行動についての歴史的な集計報酬に新しい報酬を反映させることで、Q関数を反復的に改善することができます。

ベルマン方程式の式は次のとおりです：

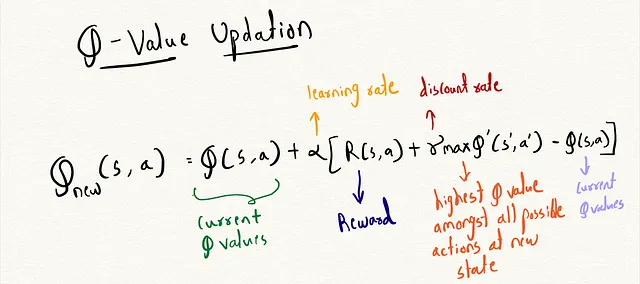
このコードでは、トレーニングのプロセスがどのように見えるかを示します：

パスの構築：パスについては、各グリッド位置の最大Q値を利用して、その位置で取る最適なアクションを決定します。Q値は、長期的な報酬に基づいて各位置で取る最善のアクションをエンコードしています。例えば、位置（0,0）のすべてのアクションkに対して、最大のQ値はアクション「1」に対応しており、右に移動することを表します。各ステップで最も高いQ値を持つアクションを貪欲に選択することで、グリッドを通る最適なパスを構築することができます。

提供されたコードを実行すると、障害物を考慮した最短パス「RBRBBB」が生成されることがわかります。

以下のリンクから、すべてのコードを1つのファイルにまとめたものを参照できます： shortest_path_rl.py

結論

現実の強化学習のシナリオでは、エージェントが相互作用する環境は非常に大きく、報酬はまれです。ボードの設定を0と1で変更することで、このハードコードされたQテーブルアプローチは一般化に失敗します。私たちの目標は、グリッドワールドの設定の一般的な表現を学び、新しいレイアウトでも最適なパスを見つけることができるエージェントをトレーニングすることです。次の投稿では、ハードコードされたQテーブルの値をDeep Q Network（DQN）で置き換えます。DQNは、状態-アクションの組み合わせと完全なグリッドレイアウトを入力とし、Q値の推定値を出力するニューラルネットワークです。このDQNにより、トレーニング中に遭遇していない新しいグリッドレイアウトでもエージェントは最適なパスを見つけることができるはずです。

もしもお気軽にお話ししたい、またはつながりたい場合は、LinkedInでご連絡ください：https://www.linkedin.com/in/pratikdaher/

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!