バイツからバイオロジーへ 第1回 コンピュータ生物学におけるLCSアルゴリズムを使ったグローバルシーケンスアラインメントの利用
Using LCS algorithm in computational biology From Bytes to Biology, Part 1 - Utilizing global sequence alignment
最長共通部分列問題とシーケンスアラインメント問題のステップバイステップの分析と、それぞれの解決策の説明を通じて、それらの類似点と相違点を強調した比較
はじめに
ようこそ!これは私の「ビットから生物学へのシリーズ」の最初のエントリであり、そこでは一般的なアルゴリズムと計算生物学/バイオインフォマティクスの間のつながりを探求し、形式的な生物学の教育を受けていない人々にとっても直感的でアクセスしやすくすることを目指しています。私は、計算生物学においても形式的な生物学のバックグラウンドは必要ないということに納得するのに時間がかかりましたが、この非常に魅力的な分野で有意義な貢献をするためには、同じような立場にいる人々にも試してみるように説得できると思います 🙂
この記事では、計算生物学における最も基本的な問題の1つであるシーケンスアラインメントについて説明します。DNA、RNA、およびタンパク質の配列のアラインメントは、進化関係の理解、機能注釈の進行、突然変異の同定、および薬物設計や精密医療の進歩など、さまざまな重要な意味を持ちます。
目次
- 最長共通部分列(LCS)- LCS概要- LCSの動的計画法による解決策- LCSのPython実装
- グローバルシーケンスアラインメント(GSA)- GSA概要- スコアリングシステム- GSAの動的計画法による解決策- GSAのPython実装
- LCS vs. グローバルシーケンスアラインメント:類似点と相違点- 要約表
最長共通部分列(LCS)問題
最長共通部分列(LCS)は、2つ以上の入力配列間で共有されるすべての有効な部分列の中で最も長い部分列を特定するクラシックなコンピューターサイエンスの問題です。
まず、部分列と部分文字列の重要な違いを注意することで、LCSの問題を明確にしてみましょう。シーケンス"ABCDE"を取ります:
- 「経済成長を遅らせることなく、量子コンピュータを導入する方法」
- 「ホワイトハウスがスマートホームのサイバーセキュリティプログラムを提案」
- 「サンノゼは歩行者の交通事故死を防ぐために人工知能を活用する方法をここで紹介します」
- 部分文字列は、元の順序で連続する文字で構成されます。たとえば、有効な部分文字列には
"ABC"、“CD”などがありますが、“ABDE”や“CBA”は含まれません。 - 一方、部分列は連続している必要はありませんが、元の順序である必要があります。たとえば、有効な部分列には
“AC”や“BFG”などがあります。
したがって、LCSは2つ以上のシーケンス間の可能な部分列の中で最も長い部分列です。以下に簡単な例を示します:

実際には、LCSは、盗作検出¹やUnixのdiffコマンドなど、はるかに大きなテキストデータを対象とする多くの応用があり、効率的で信頼性のあるスケーラブルなアルゴリズムの解決策が必要です。
LCSソリューションの形式化
LCSへの3ステップの動的計画法ソリューションの復習です:
- 初期化(シーケンス1とシーケンス2の長さがmとnであるm×n行列を作成する)。
- 再帰式に従って行列を埋めます。
- LCSとその長さを見つけるためにトレースバックします。
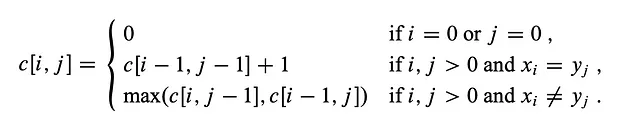
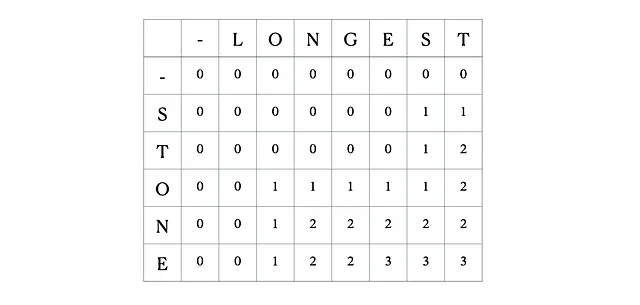
入力として“LONGEST”と“STONE”を考えます。上記の再帰関係に基づいて、DP行列を埋めてから以下のようにトレースバックします。

これが完全なDPテーブルです。
これは以下のPythonの実装に翻訳されます。
# 最長共通部分列def lcs(seq1, seq2): m = len(seq1) n = len(seq2) # DPテーブルの構築 table = [[0 for x in range(n+1)] for x in range(m+1)] # 再帰的な式(15.9)に基づいてテーブルを埋める for i in range(m+1): for j in range(n+1): if i == 0 or j == 0: # 場合1 table[i][j] = 0 elif seq1[i-1] == seq2[j-1]: # 場合2 table[i][j] = table[i-1][j-1] + 1 else: # 場合3 table[i][j] = max(table[i-1][j], table[i][j-1]) # 右下端のセルからトレースバック index = table[m][n] lcs = [""] * (index+1) lcs[index] = "" i = m j = n while i > 0 and j > 0: if seq1[i-1] == seq2[j-1]: # マッチした文字をLCSに追加 lcs[index-1] = seq1[i-1] i -= 1 j -= 1 index -= 1 elif table[i-1][j] > table[i][j-1]: i -= 1 else: j -= 1 # 最長共通部分列とその長さを出力 print("Sequence 1: " + seq1 + "\nSequence 2: " + seq2) print("LCS: " + lcs + ", length: " + str(len(lcs)))使用例:
seq1 = 'STONE'seq2 = 'LONGEST'lcs(seq1, seq2)出力:
Sequence 1: STONESequence 2: LONGESTLCS: ONE, length: 3さて、このアルゴリズムがどのように使用されるかを見てみましょう… ↓
(グローバル) シーケンスアラインメント問題
なぜDNA/RNA/タンパク質のシーケンスをアラインメントしたいのか?
直感的には、2つのシーケンスをアラインメントすることは、それらの間の同一のセグメントを見つけるタスクであり、それらの類似性のレベルを評価する最終的な目標を果たすものです。概念的には比較的簡単ですが、DNAとタンパク質のシーケンスは進化を通じて起こり得る無数の変化のため、実際には非常に複雑なものとなっています。具体的には、これらの変化の一般的な例には以下があります:
- 挿入、削除、または置換によるポイント変異:
– 挿入の例:AAA → ACAA
– 削除の例:AAA → AA
– 置換の例:AAA → AGA - 異なる遺伝子からのシーケンスまたはセグメントの融合
これらの意図しない変化は、与えられたシーケンスの理解を隠す曖昧さや違いをもたらす可能性があります。ここで、アラインメント技術を使用してシーケンス間の類似性を評価し、同義性などの特性を推測するのです。
シーケンスをどのようにアラインメントするか?
これらの進化的な変化と生物学的なシーケンスの比較の性質のため、LCSとは異なり、単に「マッチしない」要素を破棄し、共通のセグメントのみを保持するのではなく、グローバルシーケンスアラインメントではすべての文字をアラインメントする必要があります。つまり、アラインメントはしばしば3つの要素を含むことがあります:
- マッチは、一致するベースの間に
|で示されます - ミスマッチは、ミスマッチしたベースの間に空白があります
- ギャップ挿入は、ダッシュ
—で示されます
以下に例を示します。2つのDNA配列 “ACCCTG” と “ACCTGC” があるとします。これらをベースごとに一致させる方法はいくつかありますが、以下で説明した3つの操作を考慮に入れます:
ギャップ挿入なしで並べることができます:
ACCCTGT||| |ACCTGCTこの並び方には、ギャップ挿入が0回、マッチが3回、ミスマッチが3回、そして最後に1回のマッチがあります。
また、ギャップ挿入を許可する代わりに、より多くのマッチを得ることもできます:
ACCCTG-T||| || |ACC-TGCTこの並び方には、合計6回のマッチ、2つのギャップ、そして0回のミスマッチがあります(ギャップ挿入にはギャップペナルティが含まれているため、ベースとギャップのペアはミスマッチとは数えません)。
また、望むなら、以下のように並べることもできます。この場合、合計1回のマッチのみです:
-ACC-CT-GT | ACCTG-CT--任意の2つの配列の間では、ほとんどの場合、先ほど見たように技術的に正しいアラインメントを無限に生成する方法があります。それらのうちいくつかは他よりも明らかに悪いものになるでしょうが、いくつかの「ほぼ同じくらい良い」オプション(上記のオプション1と2など)も存在します。
では、各アラインメントの品質を評価し、最適なアラインメントを選び、必要ならタイブレークするにはどうすればよいのでしょうか?
スコアリングスキーム
1. ACCCTGT 2. ACCCTG-T 3. -ACC-CTGT ||| | ||| || | | ACCTGCT ACC-TGCT ACCTG-CT-上記の例では、各アラインメントには異なるマッチ数、ミスマッチ数、ギャップ数の組み合わせがあります。
LCS問題とは異なり、部分列はその長さのみで評価されるわけではなく、配列アラインメントでは、各ベースごとの対応を構成する量的なスコアリングシステムを定義することでアラインメントの品質を測定することが一般的です:
- マッチの報酬:シーケンス内でベースごとのマッチペアがある場合に全体のアラインメントスコアに追加されるスコア。
- ギャップペナルティ:ギャップを導入するたびに全体のアラインメントスコアから引かれるペナルティ値。
- ミスマッチペナルティ:ミスマッチがあるたびに全体のアラインメントスコアから引かれるペナルティ値。
この問題をアルゴリズムとして形式化するにはどうすればよいのでしょうか?
アルゴリズムの解法は、LCS問題の解法と構造的に重なります。3つのステップからなる Needleman-Wunsch アルゴリズムとしても知られます:
- 初期化(シーケンス1とシーケンス2の長さをm×n行列で作成する)
- 再帰的な式に従って行列を埋める
- 最適なアラインメントとその長さを見つけるために戻り値を追跡する

解の数学的およびPythonの形式化に入る前に、シーケンス “ACGTGTCAG” と “ATGCTAG” を使用したプロセスのイラストを以下に示します:
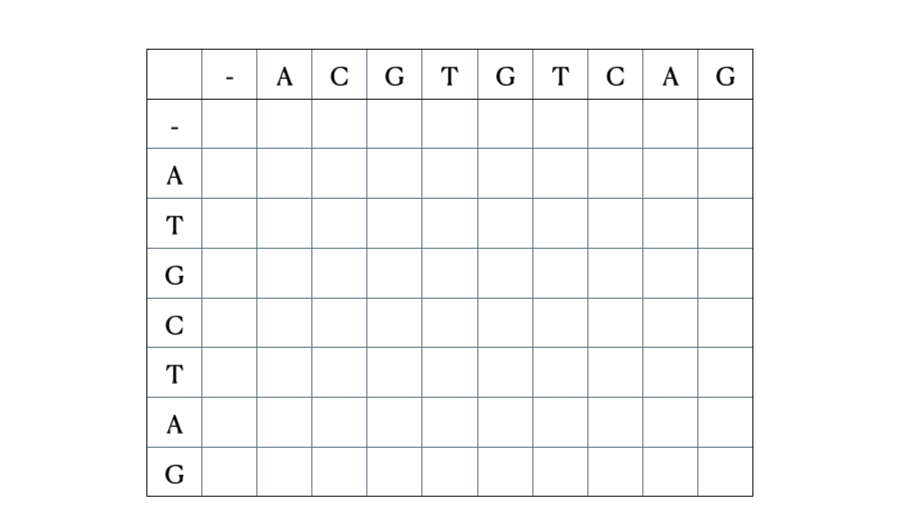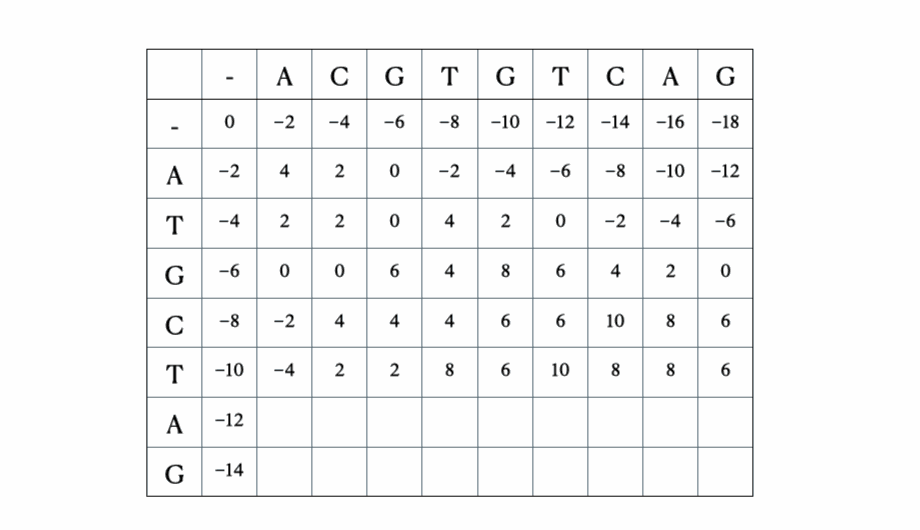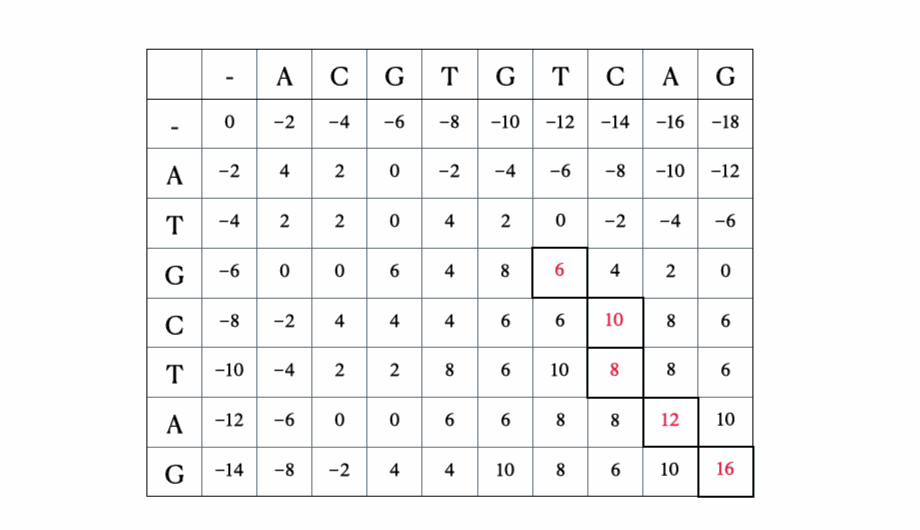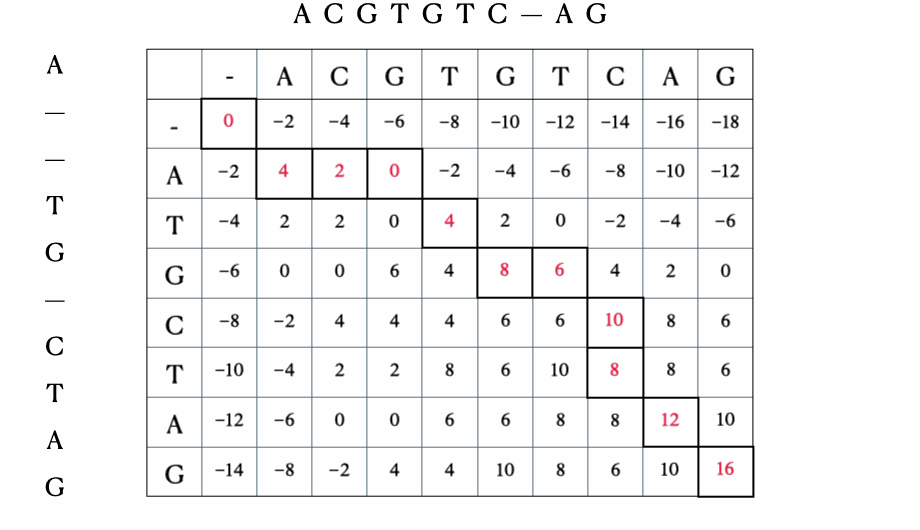
Pythonの解決策
クラスGlobalSeqAlignを使用してPythonの解決策を実装しましょう。このクラスは、行列の埋め込みとトレースバックの両方を処理します。
まず、シーケンス1、シーケンス2、マッチスコア、ミスマッチペナルティ、およびギャップペナルティの5つの重要な情報を含むオブジェクトを作成します。
class globalSeqAlign: def __init__(self, s1, s2, M, m, g): self.s1 = s1 self.s2 = s2 self.M = M self.m = m self.g = g次に、2つの塩基間のスコアを取得するヘルパー関数を定義します。塩基が一致する場合、ミスマッチの場合、または塩基ギャップのペアの場合、スコアを返します。
def base_pair_score(self, char1, char2): if char1 == char2: return self.M elif char1 == '-' or char2 == '-': return self.g else: return self.mここで、以前に見たLCS関数と非常に似た関数を定義します。この関数は、m×n行列を使用し、再帰的な式に従って埋め込み、最適なアライメントを返します。最適なアライメントは、合計スコアを最大化します。
def optimal_alignment(self, s1, s2): m = len(s1) n = len(s2) score = [[0 for x in range(n+1)] for x in range(m+1)] # スコアテーブルの計算 for i in range(m+1): # 0で初期化 score[i][0] = self.g * i for j in range(n+1): # 0で初期化 score[0][j] = self.g * j for i in range(1, m+1): # 再帰的な式に基づいて残りのセルを埋め込む for j in range(1, n+1): match = score[i-1][j-1] + self.base_pair_score(s1[j-1], s2[i-1]) delete = score[i-1][j] + self.g insert = score[i][j-1] + self.g score[i][j] = max(match, delete, insert) # 右下のセルからトレースバック align1 = "" align2 = "" i = m j = n while i > 0 and j > 0: score_curr = score[i][j] score_diag = score[i-1][j-1] score_up = score[i][j-1] score_left = score[i-1][j] if score_curr == score_diag + self.base_pair_score(s1[j-1], s2[i-1]): # 一致 align1 += s1[j-1] align2 += s2[i-1] i -= 1 j -= 1 elif score_curr == score_up + self.g: # 上向き align1 += s1[j-1] align2 += '-' j -= 1 elif score_curr == score_left + self.g: # 左向き align1 += '-' align2 += s2[i-1] i -= 1 while j > 0: align1 += s1[j-1] align2 += '-' j -= 1 while i > 0: align1 += '-' align2 += s2[i-1] i -= 1 return(align1[::-1], align2[::-1]) # 逆順で返す最適なアライメントができたら、シーケンスの一致度を定量化する分析を進めることができます。
類似性の定量化:パーセンテージの類似性
「類似性のレベル」を測定する最も簡単な方法の1つは、パーセンテージの類似性です。最適なアライメントを取り、その長さを見て、一致する領域の総長で割ります。
例:
Seq 1: ACACAGTCAT |||| |||||Seq 2: ACACTGTCAT10組のうち9組が一致するため、90%の類似性が得られます。アライメントの品質を分析するための他の多くの興味深い方法がありますが、シーケンスアライメントの基本的なメカニズムは同じです。
LCSおよびグローバルシーケンスアライメントの比較
問題とその解決策の詳細を見てきたので、LCSとグローバルシーケンスアラインメントを並べて見てみましょう。
類似点
- 目的:両方の問題は、入力シーケンスの類似性と共通要素を見つけて最大化することです。
- アルゴリズムのアプローチ:両方の問題は、動的計画法を使用して解決することができます。これにはDP行列/テーブル、行列の埋め込み、シーケンス/アラインメントの生成に戻るという手順が含まれます。
- スコアリングスキーム:両方の問題には、シーケンスマッチングの一致、不一致(およびギャップ)に関連するスコアがあります。これらのスコアは、最適な部分シーケンス/アラインメントを取得するためにアルゴリズムで明示的および暗黙に使用されます。
違い
- スコアリングシステム:- LCSは自動的に一致スコア= 1、不一致/ギャップ= 0というスコアリングスキームを採用します。- グローバルシーケンスアラインメントは、一致スコア= A、不一致ペナルティ= B、ギャップペナルティ= Cというより複雑なスコアリングスキームを持っています。
- ギャップの処理:- LCSは通常、ギャップを不一致と同等に扱います。これは部分シーケンスの定義によるもので、一致のみを保持します。- グローバルシーケンスアラインメントでは、不一致/ギャップに優先順位がある場合、ギャップにペナルティスコアが割り当てられます。
- アラインメントの長さ:- LCSは、このセグメントに含まれない要素を無視して、すべての入力に共通のセグメントを見つけることに関心があります。- グローバルシーケンスアラインメントは、入力シーケンスの長さが異なる場合でも、ギャップを挿入することを意味する場合でも、与えられたシーケンス全体に一致させます。
以下に上記のポイントの要約表があります:

結論
ここまでお付き合いいただきありがとうございます 😼!この記事では、最長共通部分列とその計算生物学への応用について詳しく取り上げ、両者を並べて比較しました。
このシリーズでは、他のトピック、例えば隠れマルコフモデル、ガウス混合モデル、分類アルゴリズムなどについても取り上げ、それらが計算生物学の特定の問題をどのように解決するかを見ていきます。お会いできるのを楽しみにしています。Happy coding ✌🏼!
[1] Baba, K., Nakatoh, T., & Minami, T. (2017). Plagiarism detection using document similarity based on distributed representation. Procedia Computer Science, 111, 382–387. https://doi.org/10.1016/j.procs.2017.06.038
[2] Cormen, T. H. (Ed.). (2009). Introduction to algorithms (3rd ed). MIT Press.
[3] Zvelebil, M. J., & Baum, J. O. (2008). Understanding bioinformatics. Garland Science.
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles

