「ベイズネットワークを使用して、病院の補助サービスの量を予測する」

Using Bayesian networks to predict the quantity of hospital support services.

診断的な入力変数を使用したPythonの例

私は医療データを扱っているので（ほぼ10年間）、将来の患者数の予測は非常に難しい問題でした。考慮すべき依存関係が非常に多いです – 患者の要求と重症度、管理上のニーズ、検査室の制約、プロバイダーが突然休んだ、大雪など。さらに、予期しないシナリオはスケジュールやリソースの割り当てに連鎖的な影響を与えることがあり、最良のExcelの予測にも反することがあります。

このような問題は、データの観点から解決しようとすると非常に興味深いです。なぜなら、それらは難しく、しばらく考えることができるからですが、わずかな改善でも大きな成果につながることがあるからです（例：患者のスループットの改善、待ち時間の短縮、満足度の高いプロバイダー、コストの削減）。

それでは、どのように解決すればよいのでしょうか？まあ、Epicは実際の患者の予約時刻の実際の記録を含む、多くのデータを提供してくれます。過去の出力がわかっているため、主に教師あり学習の領域にいますし、ベイジアンネットワーク（BN）は良い確率的グラフィカルモデルです。

ほとんどの意思決定は単一の入力で行われることができます（例：「レインコートを持っていくべきか？」、入力が「雨が降っている」であれば、答えは「はい」です）。しかし、BNはより複雑な意思決定（確率と依存関係の異なる複数の入力を含むもの）を簡単に処理できます。この記事では、症状、がんのステージ、治療目標の既知の確率に基づいて、2か月後に患者が到着する確率スコアを出力できる非常にシンプルなBNをPythonで作成します。

• 「脳活動計測と仮想現実の統合」
• 「AI規制に反対する理論は無意味である」
• 「AIコーディングツールが必要なエンジニアの数を減らすなら、予算をどこに使えばいいのか？」

ベイジアンネットワークの理解：

ベイジアンネットワークは、有向非循環グラフ（DAG）を使用して共同確率分布をグラフィカルに表現するものです。DAGのノードはランダム変数を表し、有向エッジはこれらの変数間の因果関係や条件付き依存関係を示します。すべてのデータサイエンスプロジェクトに当てはまるように、意思決定に関与するワークフロー（変数）を適切にマッピングするために、最初に利害関係者と多くの時間を費やすことは高品質な予測にとって重要です。

それでは、私は私たちの乳房腫瘍学のパートナーに会い、彼らが患者が2か月後に予約が必要かどうかを判断するために3つの変数が重要であると説明してくれるシナリオを作ります：症状、がんのステージ、治療目標。私はタイプしながらこれを作り上げていますが、それで行きましょう。

（実際には、将来の患者数に影響を与える数十の要素があります。いくつかは単一または複数の依存関係を持ち、他の要素は完全に独立していますが、それでも影響を与えます）。

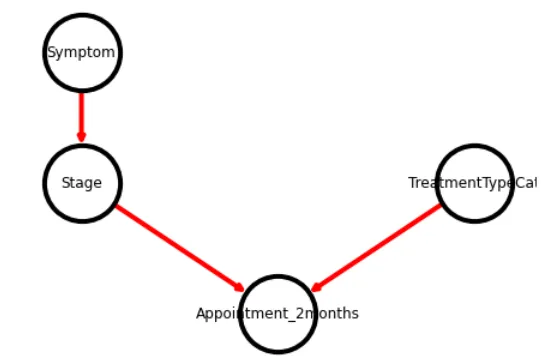
上記のようなワークフローだと言います：ステージは症状に依存しますが、治療タイプはそれらとは独立しており、また2か月後の予約にも影響を与えます。

これに基づいて、これらの変数のデータをデータソース（私たちにとってはEpic）から取得します。また、私たちのスコアノード（Appointment_2months）の既知の値（「はい」または「いいえ」）も含まれています。

# パッケージのインストールimport pandas as pd # データ操作のためのimport networkx as nx # グラフの描画のためのimport matplotlib.pyplot as plt # グラフの描画のための!pip install pybbn# ベイジアン信念ネットワーク（BBN）の作成のためのfrom pybbn.graph.dag import Bbnfrom pybbn.graph.edge import Edge, EdgeTypefrom pybbn.graph.jointree import EvidenceBuilderfrom pybbn.graph.node import BbnNodefrom pybbn.graph.variable import Variablefrom pybbn.pptc.inferencecontroller import InferenceController# 確率を手動で入力してノードを作成Symptom = BbnNode(Variable(0, 'Symptom', ['非悪性', '悪性']), [0.30658, 0.69342])Stage = BbnNode(Variable(1, 'Stage', ['Stage_III_IV', 'Stage_I_II']), [0.92827, 0.07173,                                                       0.55760, 0.44240])TreatmentTypeCat = BbnNode(Variable(2, 'TreatmentTypeCat', ['補助/新補助', '治療', '療法']), [0.58660, 0.24040, 0.17300])Appointment_2weeks = BbnNode(Variable(3, 'Appointment_2weeks', ['いいえ', 'はい']), [0.92314, 0.07686,                                                 0.89072, 0.10928,                                                 0.76008, 0.23992,                                                 0.64250, 0.35750,                                                 0.49168, 0.50832,                                                 0.32182, 0.67818])

上記のように、各変数（ノード）のレベルに対して手動で確率スコアを入力しましょう。実際には、これを実現するためにクロスタブを使用します。

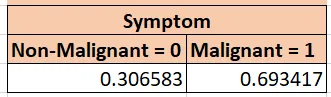
例えば、症状変数の場合、2つのレベルの頻度を取得します。約31％が非悪性であり、69％が悪性です。

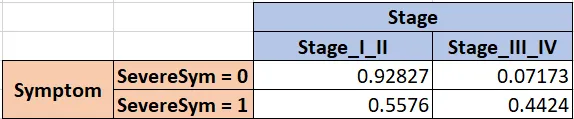
次に、次の変数であるステージを考慮し、それを症状とクロスタブします。

そして、これを繰り返し、親子のペア間のすべてのクロスタブが定義されるまで続けます。

多くのベイジアンネットワークには多くの親子関係が含まれているため、確率の計算は手間がかかる（そして主にエラーが発生しやすい）場合があります。以下の関数は、0、1、または2つの親に対応する任意の子ノードの確率行列を計算するのに役立ちます。

# この関数は確率分布を計算するのに役立ちます（注意：最大2つの親を処理できます）def probs(data, child, parent1=None, parent2=None):    if parent1==None:        # 確率を計算する        prob=pd.crosstab(data[child], 'Empty', margins=False, normalize='columns').sort_index().to_numpy().reshape(-1).tolist()    elif parent1!=None:            # 子ノードが1つまたは2つの親を持つかどうかを確認する            if parent2==None:                # 確率を計算する                prob=pd.crosstab(data[parent1],data[child], margins=False, normalize='index').sort_index().to_numpy().reshape(-1).tolist()            else:                    # 確率を計算する                prob=pd.crosstab([data[parent1],data[parent2]],data[child], margins=False, normalize='index').sort_index().to_numpy().reshape(-1).tolist()    else: print("確率頻度の計算エラー")    return prob  

次に、実際のベイジアンネットワークのノードとネットワーク自体を作成します。

# 確率を自動的に計算するために、以前の関数を使用してノードを作成しますSymptom = BbnNode(Variable(0, '症状', ['非悪性', '悪性']), probs(df, child='症状カテゴリ'))Stage = BbnNode(Variable(1, 'ステージ', ['ステージ_I_II', 'ステージ_III_IV']), probs(df, child='ステージカテゴリ', parent1='症状カテゴリ'))TreatmentTypeCat = BbnNode(Variable(2, '治療タイプカテゴリ', ['補助/新補助', '治療', '療法']), probs(df, child='治療タイプカテゴリ'))Appointment_2months = BbnNode(Variable(3, '2ヶ月後の予約', ['いいえ', 'はい']), probs(df, child='2ヶ月後の予約', parent1='ステージカテゴリ', parent2='治療タイプカテゴリ'))# ネットワークを作成しますbbn = Bbn() \    .add_node(Symptom) \    .add_node(Stage) \    .add_node(TreatmentTypeCat) \    .add_node(Appointment_2months) \    .add_edge(Edge(Symptom, Stage, EdgeType.DIRECTED)) \    .add_edge(Edge(Stage, Appointment_2months, EdgeType.DIRECTED)) \    .add_edge(Edge(TreatmentTypeCat, Appointment_2months, EdgeType.DIRECTED))# BBNを結合木に変換しますjoin_tree = InferenceController.apply(bbn)

以上です。さあ、仮想的なデータをベイジアンネットワークに入力し、出力を評価しましょう。

ベイジアンネットワークの出力の評価

まず、特定の条件を指定せずに各ノードの確率を見てみましょう。

# マージナル確率を表示するための関数を定義します# 各ノードの確率def print_probs():    for node in join_tree.get_bbn_nodes():        potential = join_tree.get_bbn_potential(node)        print("ノード:", node)        print("値:")        print(potential)        print('----------------')        # 上記の関数を使用してマージナル確率を表示しますprint_probs()

ノード: 1|ステージ|ステージ_I_II,ステージ_III_IV値:1=ステージ_I_II|0.671241=ステージ_III_IV|0.32876----------------ノード: 0|症状|非悪性,悪性値:0=非悪性|0.693420=悪性|0.30658----------------ノード: 2|治療タイプカテゴリ|補助/新補助,治療,療法値:2=補助/新補助|0.586602=治療|0.173002=療法|0.24040----------------ノード: 3|2ヶ月後の予約|いいえ,はい値:3=いいえ|0.776553=はい|0.22345----------------

このデータセットのすべての患者は、Stage_I_IIである確率が67％、非悪性である確率が69％、補助/新鮮な治療が必要である確率が58％であり、そのうちの22％の患者が2ヶ月後の予約が必要でした。

これらの情報は、ベイジアンネットワークを使用せずに単純な頻度表から容易に得ることができます。

しかし、今度はもっと条件付きの質問をしてみましょう: Stage = Stage_I_IIであり、TreatmentTypeCat = Therapyであるという条件のもとで、患者が2ヶ月後にケアを必要とする確率は何％でしょうか。また、プロバイダーはまだ患者の症状について何も知らないということを考慮してください（まだ患者を見ていないかもしれません）。

私たちは知っている情報をノードに設定します:

# To add evidence of events that happened so probability distribution can be recalculateddef evidence(ev, nod, cat, val):    ev = EvidenceBuilder() \    .with_node(join_tree.get_bbn_node_by_name(nod)) \    .with_evidence(cat, val) \    .build()    join_tree.set_observation(ev)# Add more evidenceevidence('ev1', 'Stage', 'Stage_I_II', 1.0)evidence('ev2', 'TreatmentTypeCat', 'Therapy', 1.0)# Print marginal probabilitiesprint_probs()

これにより、次の結果が返されます:

Node: 1|Stage|Stage_I_II,Stage_III_IVValues:1=Stage_I_II|1.000001=Stage_III_IV|0.00000----------------Node: 0|Symptom|Non-Malignant,MalignantValues:0=Non-Malignant|0.576020=Malignant|0.42398----------------Node: 2|TreatmentTypeCat|Adjuvant/Neoadjuvant,Treatment,TherapyValues:2=Adjuvant/Neoadjuvant|0.000002=Treatment|0.000002=Therapy|1.00000----------------Node: 3|Appointment_2months|No,YesValues:3=No|0.890723=Yes|0.10928----------------

その患者は、2ヶ月後に到着する確率がわずか11％しかありません。

品質の高い入力変数の重要性についての注意事項:

信頼性のある将来の診療予測を提供するために、BNの成功は患者ケアのワークフローの正確なマッピングに大きく依存します。似たような状態で提示される患者は、通常、類似のサービスを必要とします。その入力の変異は、臨床から行政までの特性を持ち、最終的にはサービスニーズの何らかの決定論的なパスに対応します。しかし、より複雑で予測の対象が遠くなるほど、より具体的で入念なBNが高品質の入力を必要とします。

その理由は次のとおりです:

1. 正確な表現: ベイジアンネットワークの構造は、変数間の実際の関係を反映する必要があります。適切に選択された変数や理解されていない依存関係は、予測や洞察の精度を低下させる可能性があります。
2. 効果的な推論: 品質の高い入力変数は、モデルの確率推論能力を向上させます。変数が条件付き依存性に基づいて正確に接続されている場合、ネットワークはより信頼性の高い洞察を提供できます。
3. 複雑性の低減: 関係のないまたは冗長な変数を含めると、モデルが不必要に複雑化し、計算要件が増加します。品質の高い入力はネットワークを効率化します。

読んでいただきありがとうございます。LinkedInでのご連絡をお待ちしています！データサイエンスとヘルスケアの交差点に興味がある方、または共有する興味深い課題がある方は、コメントまたはDMをお願いします。

他の記事もご覧ください:

クラスのバランス調整が過大評価されている理由

CPTコードの特徴エンジニアリング

基本的なニューラルネットワークの設計手順

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!