非教師あり学習シリーズ：階層クラスタリングの探索

Unsupervised Learning Series Exploring Hierarchical Clustering.

階層的クラスタリングがどのように機能し、ペアワイズ距離に基づいてクラスタを構築するかを探ってみましょう。

前回の非教師あり学習シリーズの投稿では、最も有名なクラスタリング方法の1つであるK-meansクラスタリングを探索しました。この投稿では、別の重要なクラスタリング技術である階層的クラスタリングの背後にある方法について説明します。

この方法も距離（ユークリッド、マンハッタンなど）に基づいており、データの階層的表現を使用してデータポイントを結合します。k-meansとは異なり、データサイエンティストが設定できるkなど、セントロイドの数に関するハイパーパラメータは含まれていません。

主に、階層的クラスタリングは、凝集型クラスタリングと分割型クラスタリングの2つに分けることができます。前者では、データポイントは単一の単位と見なされ、距離に基づいて近くのデータポイントに集約されます。後者では、すべてのデータポイントを単一のクラスタと見なし、特定の基準に基づいて分割を開始します。凝集型バージョンが最も有名で広く使用されているため（sklearnの組み込み実装はこのプロトコルに従います）、この投稿ではこの階層型を探求します。

このブログ投稿では、凝集型階層的クラスタリングを2つのステップでアプローチします。

• Rendered.aiは、合成データの生成にNVIDIA Omniverseを統合します
• 2023年に知っておく必要があるデータ分析ツール
• オープンソースツールがデータサイエンスの進歩を加速する役割

• まず、平均法（データポイントの階層を構築するために使用できる方法の1つ）を使用した凝集型クラスタリングを使用して、階層がどのように構築されるかをプレイバイプレイで分析します。
• その後、sklearnの実装を使用して実際のデータセットに階層的クラスタリングを適合させる方法についていくつかの例を示します。ここでは、階層を構築するために使用できる他の方法（ward、minimumなど）も詳細に説明します。

始めましょう！

凝集型クラスタリングの例-ステップバイステップ

ステップバイステップの例では、5人の顧客からなる架空のデータセットを使用します。

5人の顧客を抱える店を運営し、これらの顧客を類似性に基づいてグループ化したいとします。考慮したい2つの変数があります：顧客の年齢と年間収入です。

凝集型クラスタリングの最初のステップは、すべてのデータポイント間のペアワイズ距離を作成することです。 [x、y]形式で各データポイントを表すことにより、それを行ってみましょう。

• [60、30]と[60、55]の距離： 25.0
• [60、30]と[30、75]の距離： 54.08
• [60、30]と[41、100]の距離： 72.53
• [60、30]と[38、55]の距離： 33.30
• [60、55]と[30、75]の距離： 36.06
• [60、55]と[41、100]の距離： 48.85
• [60、55]と[38、55]の距離： 22.0
• [30、75]と[41、100]の距離： 27.31
• [30、75]と[38、55]の距離： 21.54
• [41、100]と[38、55]の距離： 45.10

上記で計算したペアワイズ距離のうち、どの距離が最も小さいですか？

年収が9万ドル以下の中年顧客の間の距離 — 座標[30, 75]と[38, 55]の顧客!

2つの任意の点p1とp2のユークリッド距離の式を確認すると：

近い2人の顧客を接続して2次元プロット上の最小距離を視覚化してみましょう：

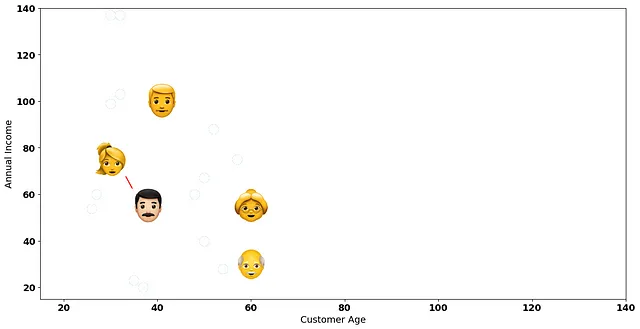
階層的クラスタリングの次のステップは、これら2人の顧客を最初のクラスターとして考慮することです！

次に、再びデータポイント間の距離を計算します。ただし、1つのクラスターにグループ化された2人の顧客は1つのデータポイントとして扱われます。たとえば、下の赤いポイントを考えてみてください。それは2つのデータポイントの間の平均に位置します。

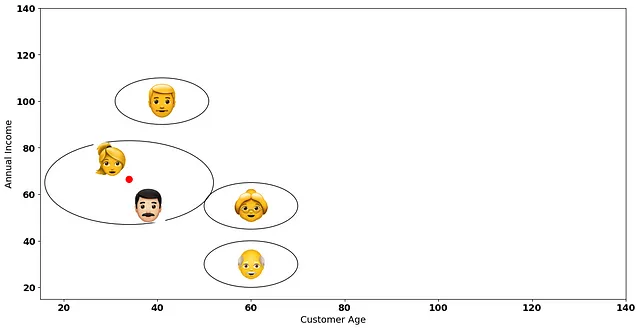
要約すると、階層的クラスタリングの次の反復では、元のデータポイント（エモジ）の座標ではなく、赤いポイント（それらのデータポイントの間の平均）を考慮します。これは平均リンケージ法で距離を計算するための標準的な方法です。

集計されたデータポイントに基づいて距離を計算するために使用できる他の方法は次のとおりです：

• 最大（または完全リンケージ）：集約しようとしているポイントに関連するクラスターで最も遠いデータポイントを考慮します。
• 最小（または単一リンケージ）：集約しようとしているポイントに関連するクラスターで最も近いデータポイントを考慮します。
• ワード（またはワードリンケージ）：次の集約でクラスターの分散を最小限に抑えます。

階層的クラスタリングでは、リンケージ方法が重要であるため、ステップバイステップの説明を少し中断してリンケージ方法に少し深く入ってみましょう。3つのマージするクラスターの架空の例に対して、階層的クラスタリングで利用可能な異なるリンケージ方法の視覚的な例を次に示します：

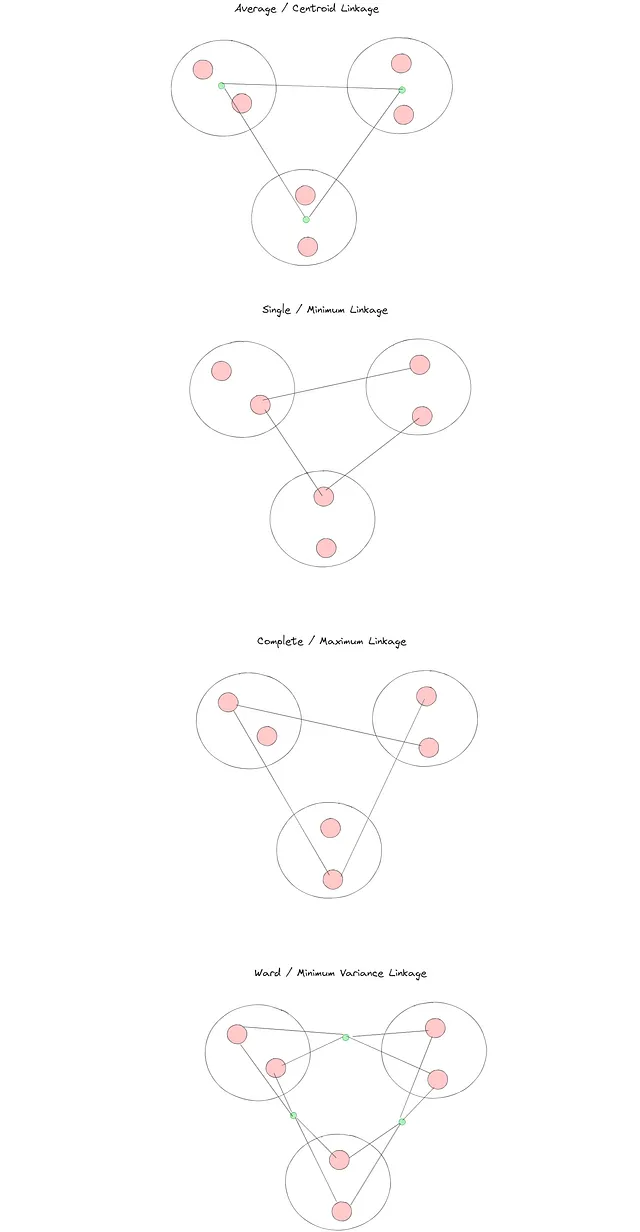
sklearnの実装では、これらのリンク方法のいくつかを試して、クラスタリング結果にかなりの違いがあることがわかります。

次に、私たちの例に戻って、新しいデータポイントのすべての距離を生成しましょう。今後、1つのクラスターとして扱われる2つのクラスターがあることを覚えておいてください：

• [60、30]と[60、55]の距離：25.0
• [60、30]と[34、65]の距離：43.60
• [60、30]と[41、100]の距離：72.53
• [60、55]と[34、65]の距離：27.85
• [60、55]と[41、100]の距離：48.85
• [34、65]と[41、100]の距離：35.69

どの距離が最短経路を持っていますか？ [60, 30] と [60, 55] の座標上のデータ点間のパスです:

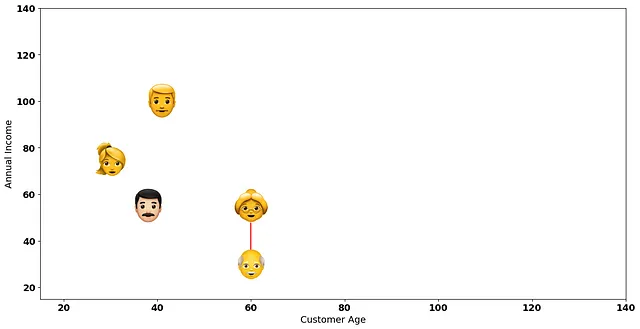
次のステップは、自然にこれらの2つの顧客を1つのクラスターに結合することです:

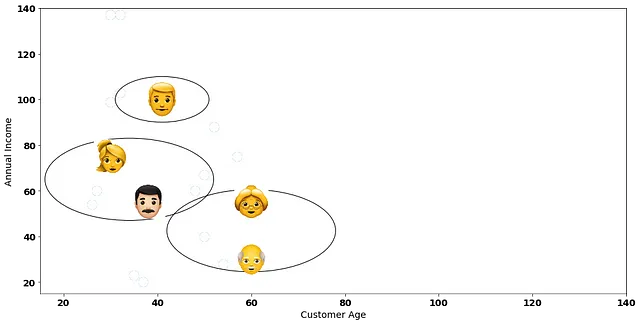
この新しいクラスターの地形ができたら、再びペアワイズ距離を計算します！ 私たちは常に、各クラスターのデータポイントの平均（選択したリンクメソッドによる）を距離計算の基準点として考慮していることを覚えておいてください:

• [60, 42.5] と [34, 65] の距離：34.38
• [60, 42.5] と [41, 100] の距離：60.56
• [34, 65] と [41, 100] の距離：35.69

興味深いことに、次に集約するデータポイントは2つのクラスターです、それらは座標[60、42.5]と[34、65]にあります:

最後に、すべてのデータポイントを1つの大きなクラスターに集約してアルゴリズムを終了します:

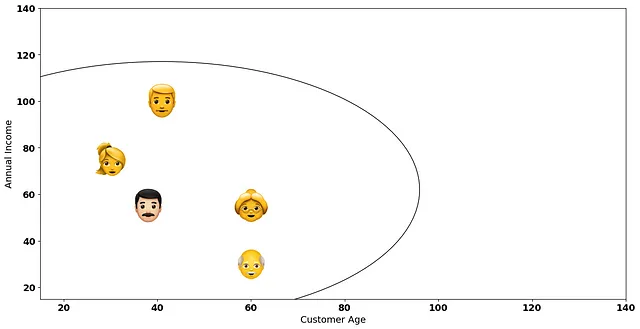
この考え方を踏まえて、私たちは正確にどこで停止するのでしょうか？全てのデータポイントを持つ1つの大きなクラスターを持つことは、あまり良いアイデアではないと思われますね？

どこで停止するかを知るには、いくつかのヒューリスティックルールを使用することができます。しかし、まず、私たちは私たが今行ったプロセスを別の方法で可視化する必要があります— デンドログラム:

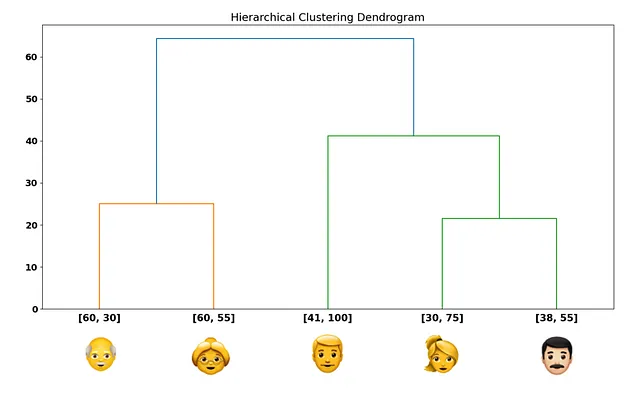
y軸には、私たちが計算した距離があります。x軸には、各データポイントがあります。各データポイントから上に向かって登ると、水平線に到達します。この水平線のy軸値は、エッジ上のデータポイントを接続する総距離を示します。

最初に1つのクラスターに接続した顧客を覚えていますか？2Dプロットで見たことがデンドログラムに一致するのは、水平線を使用して接続された最初の顧客がちょうどこれらであるためです（下からデンドログラムを登る）:

水平線は、私たちが行ったマージングプロセスを表しています！ 自然に、デンドログラムはすべてのデータポイントを接続する大きな水平線で終わります。

デンドログラムに慣れたので、sklearnの実装を確認し、このクールなクラスタリング方法に基づいて適切なクラスター数を選択する方法を理解するための実際のデータセットを使用する準備ができました！

Sklearnの実装

Sklearnの実装には、ここで利用可能なWine Qualityデータセットを使用します。

wine_data = pd.read_csv('winequality-red.csv', sep=';')wine_data.head(10)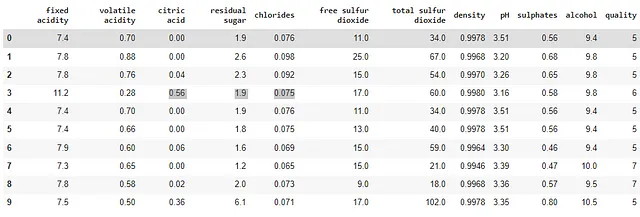

このデータセットには、クエン酸、塩化物、密度などの特性を持つワイン（特に赤ワイン）に関する情報が含まれています。データセットの最後の列は、審査員によって分類されたワインの品質に関する情報を示しています。

階層的クラスタリングは距離に対処します。ユークリッド距離を使用するため、データを標準化する必要があります。 まず、データの上にStandardScalerを使用して開始します。

from sklearn.preprocessing import StandardScalersc = StandardScaler()wine_data_scaled = sc.fit_transform(wine_data)

スケール変換されたデータセットを使用して、最初の階層的クラスタリングの解を当てはめることができます！ AgglomerativeClusteringオブジェクトを作成することで階層的クラスタリングにアクセスできます。

average_method = AgglomerativeClustering(n_clusters = None,                                          distance_threshold = 0,                                          linkage = 'average')average_method.fit(wine_data_scaled)

AgglomerativeClustering内で使用している引数について詳しく説明します。

• n_clusters=Noneは、クラスタの完全な解決策（フルデンドログラムを生成できる場所）を持つ方法として使用されます。
• distance_threshold = 0は、フルデンドログラムを生成するためにsklearn実装で設定する必要があります。
• linkage='average'は非常に重要なハイパーパラメーターです。理論的な実装では、新しく形成されたクラスタ間の距離を考慮する方法を1つ説明しました。 averageは、新しく形成されたすべてのクラスタの平均点を新しい距離の計算に考慮する方法です。sklearn実装では、single、complete、およびwardの3つの他の方法があります。

モデルを当てはめた後は、デンドログラムをプロットする時間です。これには、sklearnドキュメントで提供されるヘルパー関数を使用します。

from scipy.cluster.hierarchy import dendrogramdef plot_dendrogram(model, **kwargs):    # Create linkage matrix and then plot the dendrogram    # create the counts of samples under each node    counts = np.zeros(model.children_.shape[0])    n_samples = len(model.labels_)    for i, merge in enumerate(model.children_):        current_count = 0        for child_idx in merge:            if child_idx < n_samples:                current_count += 1  # leaf node            else:                current_count += counts[child_idx - n_samples]        counts[i] = current_count    linkage_matrix = np.column_stack(        [model.children_, model.distances_, counts]    ).astype(float)    # Plot the corresponding dendrogram    dendrogram(linkage_matrix, **kwargs)

次に、階層的クラスタリングの解をプロットします。

plot_dendrogram(average_method, truncate_mode="level", p=20)plt.title('Dendrogram of Hierarchical Clustering - Average Method')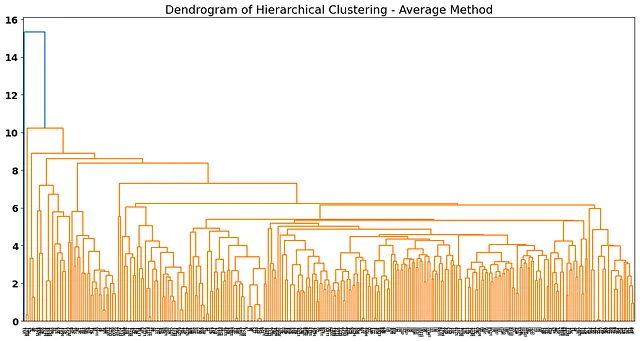

デンドログラムは、観察値が少し混み合っているように見えるため、素晴らしくありません。 average、single、completeのリンク、特にデータに強い外れ値がある場合、奇妙なデンドログラムになる場合があります。このタイプのデータにはward法が適している場合があるため、この方法をテストしてみましょう。

ward_method = AgglomerativeClustering(n_clusters = None,                                          distance_threshold = 0,                                          linkage = 'ward')ward_method.fit(wine_data_scaled)plot_dendrogram(ward_method, truncate_mode="level", p=20)

より良くなりました！デンドログラムによると、クラスターがより定義されているように見えます。ワード法は、新しく形成されたクラスター間の内部分散を最小化することによってクラスターを分割しようとします（ https://online.stat.psu.edu/stat505/lesson/14/14.7 ）このポストの最初の部分で説明したように。目的は、各反復において、集約されるクラスターが分散（データポイントと新しい形成されるクラスター間の距離）を最小化することです。

また、AgglomerativeClustering関数内のlinkageパラメータを変更することで、方法を変更できます！

ワード法のデンドログラムの外観に満足しているため、この解決策をクラスタープロファイリングに使用します:

何個のクラスターを選ぶべきか予想できますか？

距離によると、各クラスターが比較的遠いように見えるこの点でデンドログラムをカットすることが良い候補です:

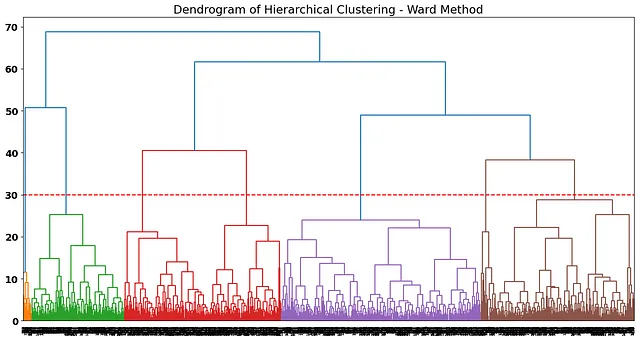
ラインが横断する垂直線の数は、私たちの解決策の最終クラスターの数です。クラスターの数を選択することは非常に「科学的」ではなく、ビジネスの解釈によって異なるクラスタリングソリューションの数が得られる場合があります。たとえば、私たちの場合、デンドログラムを少し上部でカットして最終ソリューションのクラスター数を減らすことも仮説になるかもしれません。

私たちは7つのクラスターソリューションに固執することにしました。したがって、そのn_clustersを考慮してwardメソッドを適合させましょう:

ward_method_solution = AgglomerativeClustering(n_clusters = 7,                                         linkage = 'ward')wine_data['cluster'] = ward_method_solution.fit_predict(wine_data_scaled)

元の変数に基づいてクラスターを解釈したいため、スケーリングされたデータにpredictメソッドを使用します（距離はスケーリングされたデータセットに基づいています）が、クラスターを元のデータセットに追加します。

cluster変数を条件に各変数の平均を使用して、クラスターを比較しましょう:

wine_data.groupby([‘cluster’]).mean()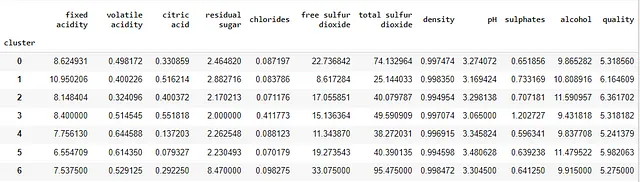

興味深いことに、データについていくつかの洞察が得られ始めます。たとえば：

• 低品質のワインはtotal sulfur dioxideの値が大きい傾向があります。最高の平均品質クラスターと低品質クラスターの間の違いに注目してください：

そして、これらのクラスタ内のワインの品質を比較すると：

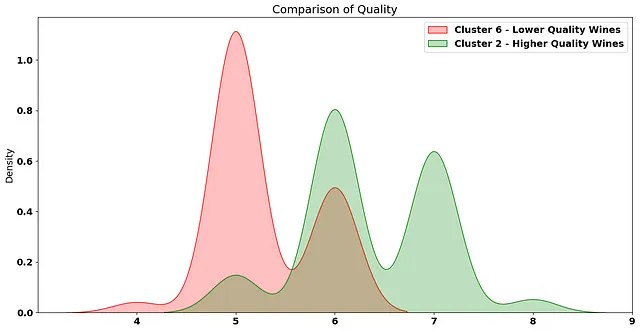
平均的に、クラスタ2にはより高品質なワインが含まれていることが明らかです。

別の興味深い解析方法は、クラスタ化されたデータの平均値間で相関行列を作成することです：

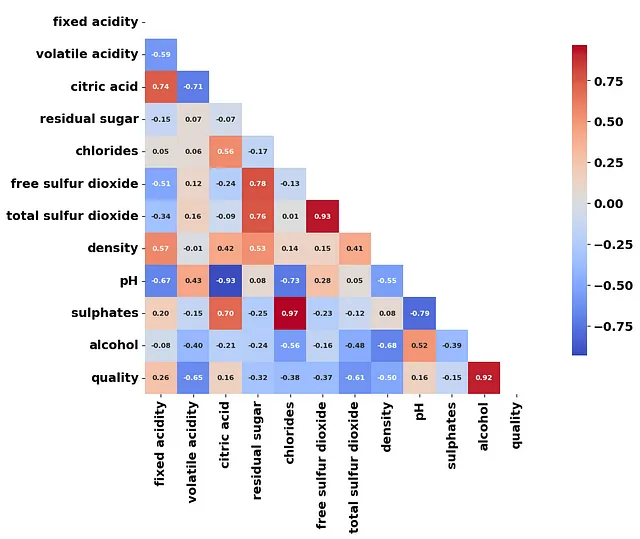
これにより、探索できる潜在的なことについての良いヒントが得られます（教師あり学習においても）。たとえば、多次元レベルで、硫酸塩および塩化物が高いワインは一緒にまとめられる可能性があります。また、アルコール度数の高いワインは、より高品質なワインと関連している傾向があることが別の結論です。

結論

以上です！教師なし学習に関するこのブログ投稿を読んでいただき、ありがとうございます。私はこのシリーズにさまざまな方法を紹介するために、さらに多くの教師なし学習アルゴリズムを追加し続けます。

もちろん、階層的クラスタリングにはいくつかの利点と欠点があります：

• アルゴリズムの大きな欠点は、最終的な解決策に到達するためにあまりにも多くのヒューリスティックスが必要になる場合があることです。デンドログラム分析、距離ベースの分析、またはシルエット係数の方法の組み合わせを適用して、意味のあるクラスタ数に到達する必要があります。また、クラスタリングトラップに陥ることを避けるために、ビジネスデータに関するいくつかの知識をこれらの技術的なアプローチと交差させることが必要です。
• また、階層的クラスタリングアプローチは非常に説明可能であり、データ内の隠れた構造を明らかにするのに役立ちます。
• さらに、階層的クラスタリングは重心初期化問題に苦しむことがないため、一部のデータセットにとっては優位に働くことがあります。

階層的クラスタリングは、顧客セグメンテーション、外れ値分析、多次元遺伝子発現データの分析、文書クラスタリングなど、さまざまなアプリケーションに適用されている非常に有名なクラスタリング方法です。

• 次のリンクで示されるように、この投稿で使用されたデータセットはクリエイティブ・コモンズ・ライセンス・国際4.0（CC BY 4.0）の下でライセンスされています：https://archive.ics.uci.edu/dataset/186/wine+quality

データサイエンティストは、この非常にクールなメソッドをツールベルトに備えている必要があります。次のプロジェクトで試してみてください。この教師なし学習シリーズのさらなる投稿にご期待ください！

この投稿で使用されたデータセットは、以下のリンクに記載されているように、クリエイティブ・コモンズ・ライセンス・国際4.0（CC BY 4.0）の下でライセンスされています：https://archive.ics.uci.edu/dataset/186/wine+quality

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!