超幾何分布の理解

Understanding hypergeometric distribution.

データサイエンスであまり知られていない分布の1つを解説

背景

二項分布は、データサイエンスの内外でよく知られた分布です。しかし、そのより人気のないいところのいとこ、超幾何分布について聞いたことがありますか？もしない場合は、この投稿がそれが何であるか、そしてなぜ私たちデータサイエンティストにとって役立つのかについての詳細な説明を与えます。

直感

超幾何分布は、母集団に関する情報を与えられた状況下で、n回の試行（サンプル）でのk回の成功の確率を、交換なしで測定します。これは、交換なしでサンプリングする点を除いて、二項分布と非常に似ています。このため、各成功（または結果）の確率は、抽選/試行ごとに変化します。一方、二項分布では成功（および失敗）の確率が固定されています。

理解しやすい例として、標準のトランプカードデッキから20枚のカードのランダムサンプルから4つのキングを引く確率を決定することが挙げられます。キングを引いた場合、母集団の構成が変わったため、次のキングを引く確率は最初と異なります。したがって、成功確率は動的です。

理論

超幾何分布の確率質量関数（PMF）は次のようになります：

• SparkとPlotly Dashを使用したインタラクティブで洞察力のあるダッシュボードの開発
• GPT-4 新しいOpenAIモデル
• データアナリストは良いキャリアですか？

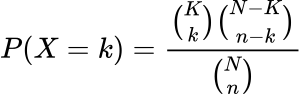
ここで：

• nは試行回数です
• kは成功回数です
• Nは母集団のサイズです
• Kは母集団内の成功数の合計です
• Xは、超幾何分布からのランダム変数です

興味のある読者は、ここでPMFの導出を見つけることができます。

角括弧のような表記は、二項係数を示しています：

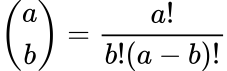
階乗は、組み合わせと順列で扱っていることを示しています。これについては、以前のブログで詳しく説明しています：

組み合わせと順列の基礎

組み合わせと順列とその違いについての簡潔な説明

towardsdatascience.com

分布の平均値は、次のようになります：

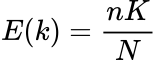
例

前回の例である、標準のトランプカードデッキからランダムに20枚のカードを選んで4つのキングを引く確率に戻りましょう。私たちが持っている情報は：

• N = 52：デッキ内のカードの数
• n = 20：サンプルするカードの数
• k = 4：望んでいるキングの数（成功回数）
• K = 4：デッキ内のキングの数

これらの数字をPMFに代入すると：

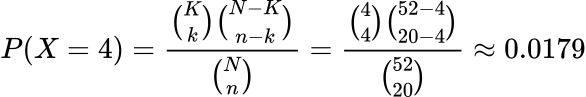
したがって、確率は非常に低いです。これは、デッキからキングを選択する確率が~0.077（1/13）であるため、さらに小さなサンプルでは、上記で示したようにさらに減少するためです。

数値や異なるシナリオで遊びたい場合は、こちらの超幾何分布計算機にリンクしています。

コードとプロット

上記の例は、超幾何分布の適用の有用なデモンストレーションです。しかし、成功の数kの関数としてPMFをプロットすることによって、より完全なイメージを得ることができます。

以下は、上記の例で、望むキングの数kを変化させたPythonによるプロットです：

GitHub Gist by author.

上記のサンプル20枚から5枚のキングを取得する確率は0であるため、キングを5枚取る確率は0です！取得する最も可能性が高いキングの数は1です。

今度は、新しい問題を考えてみましょう。ランダムに選択した30枚のサンプルからスペードスーツのカードの超幾何分布は何ですか？

GitHub Gist by author.

30枚のサンプルで最も可能性が高いスペードの数は8です。プロットによって示されるように、私たちがサンプルでスペードを取得しない可能性はほとんどありません。

応用

超幾何分布は、以下を含む多くの分野に触れています：

• ポーカーでの勝率
• 投票人口分析
• 製造業における品質管理
• 人口内の遺伝的変異

したがって、超幾何分布は、データサイエンスのキャリアでほぼ確実に遭遇するものであり、それだけでも知っている価値があります。

要約とさらなる考察

この記事では、超幾何分布について説明しました。これは、成功の確率が置き換えなしでサンプリングするために変化するため、二項分布と非常に似ています。この分布は、データサイエンスにおいて非常に強力であり、品質管理やギャンブル産業に応用されています。したがって、データサイエンティストとして知っている価値があります。

完全なコードは、次の場所で利用可能です：

VoAGI-Articles/Statistics/Distributions/hypergeometric.py at main · egorhowell/Medium-Articles

私がVoAGIブログ/記事で使用するコード。 egorhowell/Medium-Articlesのアカウントを作成して開発に貢献してください。

github.com

参照

• 超幾何分布に関する詳細情報：https://brilliant.org/wiki/hypergeometric-distribution/
• 理論的なアプローチ：https://dlsun.github.io/probability/hypergeometric.html

私とつながる！

• VoAGIで無制限のストーリーを読むには、こちらでサインアップしてください！ 💜
• 投稿時に更新を取得するには、ここでメール通知にサインアップしてください！ 😀
• LinkedIn 👔
• Twitter 🖊
• GitHub 🖥
• Kaggle 🏅

(すべての絵文字は、オープンソースの絵文字およびアイコンプロジェクトであるOpenMojiによって設計されています。ライセンス：CC BY-SA 4.0)

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!