ベイジアンマーケティングミックスモデルの理解：事前仕様に深く入り込む

Understanding Bayesian Marketing Mix Models Delving into Prior Specifications

GoogleのLightweightMMMを使ってモデル仕様を探索する

ベイズマーケティングミックスモデリングは、特にLightweightMMM（Google）やPyMC Marketing（PyMC Labs）などのオープンソースツールがリリースされたことで、ますます注目を集めています。これらのフレームワークはベイズモデリングの複雑さを簡素化していますが、ユーザーが基本的なベイズコンセプトを理解し、モデル仕様を理解できることは重要です。

この記事では、GoogleのLightweightMMMを実際の例として取り上げ、このフレームワークの事前仕様の直感と意味を示します。Pythonとscipyライブラリを使用して、事前サンプルのシミュレーションを実証します。

データ

私はRobynがMITライセンスで公開したデータを使用しています。

データセットには、以下が含まれます。

• 類似検索、パート5：局所性鋭敏ハッシュ（LSH）
• AI医療診断はどのように動作しますか？
• AIの未来を形作る ビジョン・ランゲージ・プリトレーニング・モデルの包括的な調査と、ユニモーダルおよびマルチモーダルタスクにおける役割

• 5つのメディア支出チャネル： tv_S、ooh_S、print_S、facebook_S、search_S
• 露出情報（Impression、Clicks）も持つメディアチャネル2つ：facebook_I、search_clicks_P
• 支出のない有機メディア：newsletter
• コントロール変数：events、holidays、競合他社の売上（ competitor_sales_B)

LightweightMMMモデル仕様

LightweightMMMモデルの仕様は次のとおりです：

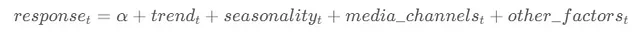
この仕様は、特定の時点tでの応答（ターゲット変数）の値を説明する加算線形回帰モデルを表します。

方程式の各構成要素を分解してみましょう。

• α：この構成要素は、応答の切片または基準値を表します。すべての他の要因がゼロのときの応答の期待値です。
• trend：この構成要素は、時間の経過に伴う応答の増加または減少の傾向を捉えます。
• seasonality：この構成要素は、応答の周期的な変動を表します。
• media_channels：この構成要素は、メディアチャネル（テレビ、ラジオ、オンライン広告）の応答への影響を考慮します。
• other_factors：この構成要素は、天気、経済指標、競合他社の活動など、応答に影響を与える他の変数を包括します。

以下では、各構成要素について詳しく説明し、事前仕様の解釈方法を説明します。事前分布は、基礎となるデータの知識がない場合に、あるパラメーターの仮定された分布を表します。

切片

切片は、標準偏差が2の半正規分布に従うように定義されています。半正規分布は、正の値に制限された正規分布に似た連続的な確率分布です。分布は、単一のパラメータである標準偏差（スケール）によって特徴付けられます。半正規分布は、切片が正の値しか取得できないことを示します。

以下のコードは、スケールが2の半正規分布の事前分布からサンプルを生成し、確率密度関数（PDF）を視覚化します。他の構成要素の視覚化については、Githubリポジトリの付属ソースコードを参照してください。

from scipy import statsscale = 2halfnormal_dist = stats.halfnorm(scale=scale)samples = halfnormal_dist.rvs(size=1000)plt.figure(figsize=(20, 6))sns.histplot(samples, bins=50, kde=False, stat='density', alpha=0.5)sns.lineplot(x=np.linspace(0, 6, 100),       y=halfnormal_dist.pdf(np.linspace(0, 6, 100)), color='r')plt.title(f"スケール={scale}の半正規分布")plt.xlabel('x')plt.ylabel('P(X=x)')plt.show()

トレンド

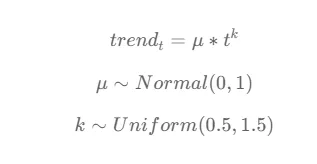
トレンドは、時間tとトレンド値の間のべき乗則の関係として定義されます。パラメータμは、トレンドの振幅または大きさを表し、kはトレンドの急峻さまたは曲率を制御します。

パラメータμは、平均が0で標準偏差が1の正規分布から描かれます。これは、μが0を中心に標準偏差1の標準正規分布に従うことを意味し、μが正または負の値を取ることができることを示します。

パラメータkは、0.5から1.5の一様分布から描かれます。一様分布により、トレンドの合理的かつ意味のある曲率を示す値を取ることができます。

以下のプロットは、事前分布から得られた別々のコンポーネントを示しています：切片とトレンドのサンプル、それぞれ個別に表されます。

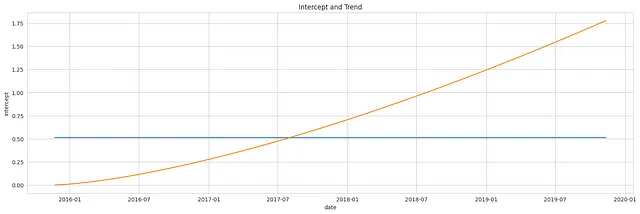
季節性

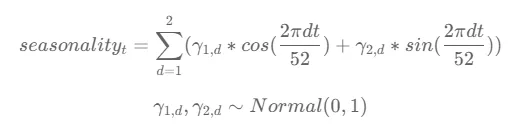
各コンポーネントγは、平均が0で標準偏差が1の正規分布から描かれます。

cosineおよびsine関数を異なるγと組み合わせることで、データに存在する季節性を捉えるための循環的なパターンがモデル化されます。cosineおよびsine関数は、52単位（週）の期間中に観察される振動的な振る舞いを表します。

以下のプロットは、事前分布から得られた季節性、切片、およびトレンドのサンプルを示しています。

その他の要因（制御変数）

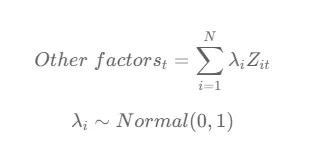
各因子係数λは、平均が0で標準偏差が1の正規分布から描かれます。これは、λが、それぞれの要因が結果に与える影響の方向と大きさを表す正または負の値を取ることができることを意味します。

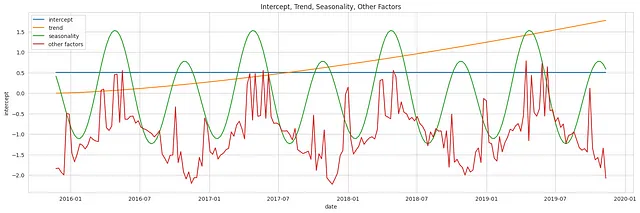
以下のプロットは、事前分布から得られた別々のコンポーネントを示しています：切片、トレンド、季節性、および制御変数（competitor_sales_B、newsletter、holidays、およびevents）のサンプルがそれぞれ個別に表されます。

メディアチャンネル

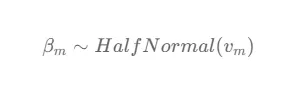
メディアチャンネルmのβ係数の分布は、標準偏差パラメータvがメディアチャンネルmに関連する総コストの合計によって決定される半正規分布で指定されます。総コストは、その特定のメディアチャンネルに割り当てられた投資やリソースを反映しています。

メディア変換

これらの方程式では、広告在庫やヒル飽和などの一連の変換を使用して、メディアチャンネルの振る舞いをモデル化しています。

PyMC3を使用したマーケティングミックスのモデリング

事前分布、データ正規化、Robyn、FacebookのオープンソースMMMとのベイジアンモデリングの比較についての実験…

towardsdatascience.com

メディアチャンネルの変換値は、時点tでの変換済みメディアチャンネルを表します。生のメディアチャンネル値xに変換を適用して得られます。ヒル変換は、半飽和点（0 ＜k≤1）を制御するパラメータK、および曲線の急峻さを制御する形状Sによって制御されます（s＞0）。

変数x∗は、広告在庫変換を受けた後の時点tでの変換済みメディアチャンネル値を表します。現在の生のメディアチャンネル値に、前の変換済み値と広告在庫の減衰パラメータλの積を加算することによって計算されます。

パラメータKとSは、形状とスケールパラメータの両方を1に設定したガンマ分布に従い、λは形状パラメータが2、スケールパラメータが1のベータ分布に従います。

ヒル飽和のパラメータKとSの確率密度関数は、以下のプロットに示されています。

shape = 1scale = 1gamma_dist = stats.gamma(a=shape, scale=scale)samples = gamma_dist.rvs(size=1000)plt.figure(figsize=(20, 6))sns.histplot(samples, bins=50, kde=False, stat='density', alpha=0.5)sns.lineplot(x=np.linspace(0, 6, 100), y=gamma_dist.pdf(np.linspace(0, 6, 100)), color='r')plt.title(f"Gamma Distribution for $K_m$ and $S_m$ with shape={shape} and scale={scale}")plt.xlabel('x')plt.ylabel('P(X=x)')# Show the plotplt.show()python

広告在庫パラメータλの確率密度関数は、以下のプロットに示されています。

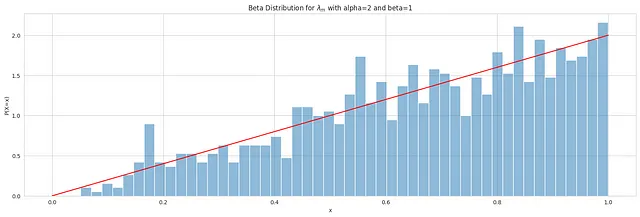
広告在庫パラメータλの仕様に関する注記：

Beta(α = 2, β = 1)分布の確率密度関数は、より高い値がより高い確率密度を持つことを示しています。メディア分析では、異なる産業やメディアアクティビティによっては、一般に小さな減衰率を示すメディアチャンネルが多い場合があります。例えば、Robynは一般的なメディアチャンネルのλ減衰の以下の範囲を示唆しています：TV（0.3〜0.8）、OOH/Print/Radio（0.1〜0.4）、digital（0〜0.3）。

Beta(α = 2, β = 1)分布の文脈では、λ値に近い確率が高くなり、0に近い値には低い確率が割り当てられます。そのため、区間[0、1]の上端付近の結果または観測値が、下端付近の結果または観測値よりもより頻繁に発生する傾向があります。

また、キャリーオーバーとシェイプエフェクトを備えたメディアミックスモデリングのベイジアン方法では、減衰パラメータはBeta(α = 3, β = 3)と定義されており、その確率密度関数は以下のようになります。この分布は、[0、1]の区間の両端と中心付近で観測結果が同様に発生する可能性があることを示しています。

以下のプロットは、事前分布から得られた別々のコンポーネントを描画しています。それぞれ、切片、トレンド、季節性、制御変数、メディアチャンネルが個別に表されています。

すべてのコンポーネントを組み合わせる

前述のように、LightweightMMMは、切片、トレンド、季節性、メディアチャンネルなど、さまざまなコンポーネントを事前分布からサンプリングし、予測応答を得るために加算的な線形回帰をモデル化します。以下のプロットは、真の応答と、事前予測分布からサンプリングされた期待される応答を視覚化しています。

1つのサンプルを真の応答値に対して視覚化することで、特定のパラメータ値のセットに対してモデルの予測が実際の結果と比較してどのようになるかを観察することができます。これにより、その特定のインスタンスでモデルのパフォーマンスを直感的に理解することができます。

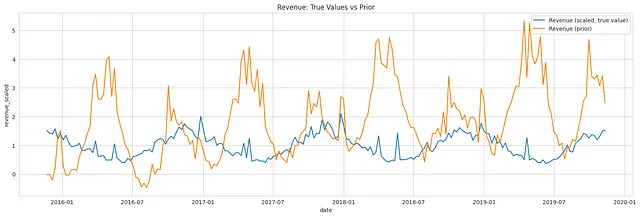
事前予測チェック

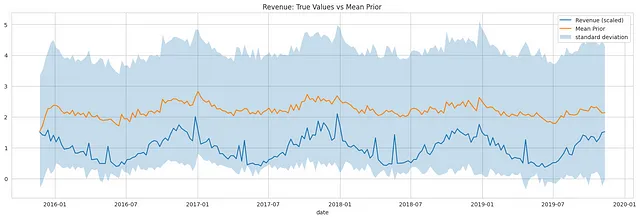
より堅牢な洞察を得るためには、事前予測分布から複数回サンプリングし、不確実性を測定することが一般的に推奨されます。事前予測チェックは、実際のデータを観察する前に、選択したモデルの適切性を評価し、モデルの予測が私たちの期待に沿っているかを評価するのに役立ちます。

以下に描かれたプロットは、期待収益（平均）と不確実性の尺度を示して、事前予測分布を視覚化しています。真の収益が標準偏差の範囲内にあることから、モデル仕様が観測されたデータに適していることがわかります。

結論

ベイズマーケティングミックスモデリングは、習得にかなりの時間がかかる場合があります。この記事が事前分布とベイズマーケティングモデルの仕様に対する理解を深めるのに役立てば幸いです。

完全なコードは、私のGithubリポジトリからダウンロードできます。

読んでくださってありがとうございました！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!