Rにおける二元配置分散分析

Two-way ANOVA in R.

Rで二要因分散分析を行う方法を学びます。また、その目的、仮説、前提条件、および結果の解釈方法も学びます。

はじめに

二要因分散分析（analysis of variance）は、2つのカテゴリ 変数が量的連続変数に与える同時的な効果を評価 する統計的手法です。

二要因分散分析は、1つのカテゴリ変数ではなく、2つのカテゴリ変数の数字反応に及ぼす効果を評価できるため、1要因分散分析の拡張版です。二要因分散分析の利点は、3番目の変数の影響を考慮しながら、2つの変数の関係をテストできることです。さらに、2つのカテゴリ変数の可能な相互作用を反応に含めることもできます。

1要因分散分析と2要因分散分析の利点は、相関と多重線形回帰の利点に非常に似ています：

• 相関は、2つの量的変数の関係を測定します。多重線形回帰も2つの変数の関係を測定しますが、この場合は他の共変量の潜在的な影響を考慮します。
• 1要因分散分析は、グループ間で量的変数が異なるかどうかをテストします。2要因分散分析もまた、グループ間で量的変数が異なるかどうかをテストしますが、この場合は別の質的変数の影響を考慮します。

以前、Rで1要因分散分析について説明しました。今回は、なぜ、いつ、どのように2要因分散分析を実行するかを紹介します。

• アルゴリズム取引と金融におけるAIにおける知的財産権法の理解
• デイビッド・オーターさんがNOMIS 2023年度の著名科学者に選ばれました
• テクニカルアーティストがNVIDIA Omniverse USD Composerを使用して、優れたウールリーマンモスを構築しました今週の「In the NVIDIA Studio」

さらに進む前に、混乱を避けるために、いくつかの関連する統計的手法とテストについて簡単に説明します：

Studentのt検定は、1つのカテゴリ変数が量的連続変数に与える影響を評価するために使用されます。 カテゴリ変数が正確に2つのレベルを持つ場合 ：

• 観測値が独立である場合は、独立サンプルのStudentのt検定を使用します（例：女性と男性の年齢を比較する場合）
• 観測値が依存している場合、つまりペアで測定される場合（同じ被験者が2回、例えば治療前と治療後に測定される場合）は、ペアサンプルのStudentのt検定を使用します

1つのカテゴリ変数が量的変数に与える影響を評価するには、カテゴリ変数が3つ以上のレベルを持つ場合 ：

• グループが独立している場合、つまり、治療Aを受けた患者のグループ、治療Bを受けた患者のグループ、治療を受けていないか偽薬を受けた患者のグループなどの場合は、1要因分散分析（単にANOVAとも呼ばれます）を使用します。
• グループが依存している場合、つまり、同じ被験者が3回、例えば治療前、治療中、治療後に測定される場合は、反復測定分散分析を使用します。

2要因分散分析は、2つのカテゴリ変数（およびその潜在的な相互作用）が量的連続変数に与える影響を評価するために使用されます。これがこの記事のトピックです。

線形回帰は、1つまたは複数の独立変数と量的連続従属変数の関係を評価するために使用されます：

• 独立変数が1つだけの場合は、単回帰と呼ばれます（量的または質的である場合があります）
• 独立変数が少なくとも2つある場合は、多重線形回帰と呼ばれます（量的、質的、または両方の混合である場合があります）

ANCOVA（共分散分析）は、定量的な変数の影響を制御しながら、カテゴリ変数が量的変数に与える影響を評価するために使用されます。 ANCOVAは、1つの質的変数と1つの定量的変数の混合である多重線形回帰の特殊な場合です。

この記事では、2要因分散分析の有用性、準備的な記述統計分析の実施方法、Rでの2要因分散分析の実施方法、結果の解釈および可視化方法について説明します。また、基礎となる前提条件を検証する方法についても簡単に説明します。

データ

二元配置分散解析をRで実行する方法を説明するため、{palmerpenguins}パッケージから入手可能なpenguinsデータセットを使用します。

私たちはデータセットをインポートする必要はありませんが、まずパッケージをロードしてからデータセットを呼び出す必要があります。

# install.packages("palmerpenguins")library(palmerpenguins)

dat <- penguins # rename datasetstr(dat) # structure of dataset

## tibble [344 × 8] (S3: tbl_df/tbl/data.frame)##  $ species          : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...##  $ island           : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...##  $ bill_length_mm   : num [1:344] 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42 ...##  $ bill_depth_mm    : num [1:344] 18.7 17.4 18 NA 19.3 20.6 17.8 19.6 18.1 20.2 ...##  $ flipper_length_mm: int [1:344] 181 186 195 NA 193 190 181 195 193 190 ...##  $ body_mass_g      : int [1:344] 3750 3800 3250 NA 3450 3650 3625 4675 3475 4250 ...##  $ sex              : Factor w/ 2 levels "female","male": 2 1 1 NA 1 2 1 2 NA NA ...##  $ year             : int [1:344] 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...

データセットには、以下の8つの変数があり、344羽のペンギンに関する情報がまとめられています：

summary(dat)

##       species          island    bill_length_mm  bill_depth_mm  ##  Adelie   :152   Biscoe   :168   Min.   :32.10   Min.   :13.10  ##  Chinstrap: 68   Dream    :124   1st Qu.:39.23   1st Qu.:15.60  ##  Gentoo   :124   Torgersen: 52   Median :44.45   Median :17.30  ##                                  Mean   :43.92   Mean   :17.15  ##                                  3rd Qu.:48.50   3rd Qu.:18.70  ##                                  Max.   :59.60   Max.   :21.50  ##                                  NA's   :2       NA's   :2      ##  flipper_length_mm  body_mass_g       sex           year     ##  Min.   :172.0     Min.   :2700   female:165   Min.   :2007  ##  1st Qu.:190.0     1st Qu.:3550   male  :168   1st Qu.:2007  ##  Median :197.0     Median :4050   NA's  : 11   Median :2008  ##  Mean   :200.9     Mean   :4202                Mean   :2008  ##  3rd Qu.:213.0     3rd Qu.:4750                3rd Qu.:2009  ##  Max.   :231.0     Max.   :6300                Max.   :2009  ##  NA's   :2         NA's   :2

このポストでは、以下の3つの変数に焦点を当てます：

• species：ペンギンの種（Adelie、Chinstrap、Gentoo）
• sex：ペンギンの性別（女性および男性）
• body_mass_g：ペンギンの体重（グラム単位）

必要に応じて、このデータセットに関する詳細情報は、Rで?penguinsを実行することで確認できます。

body_mass_gは数量的連続変数であり、従属変数であり、一方、speciesとsexはどちらも質的変数です。

これらの最後の変数は、独立変数または要因とも呼ばれる自立変数になります。Rによって要因として読み取られるようにしてください。もしそうでない場合は、要因に変換する必要があります。

二要因分散分析の目的と仮説

先述したように、二要因分散分析は、一つの量的連続変数に対して二つのカテゴリー変数の影響を同時に評価するために使用されます。

2つの独立カテゴリー変数によって形成されたグループを比較しているため、「二つの」分散分析と呼ばれます。

ここでは、体重が種と/または性別に依存するかどうかを知りたいと思っています。特に、以下に興味があります。

1. 種と体重の関係を測定および検定すること
2. 性別と体重の関係を測定および検定すること
3. 雌雄によって種と体重の関係が異なるかどうかを確認すること（つまり、性別と体重の関係が種に依存するかどうかを確認することと同じ）

最初の2つは「主効果」と呼ばれ、3つ目は「相互作用効果」として知られています。

主効果は、他の独立変数を制御することで、少なくとも1つのグループが別のグループと異なるかどうかを検定するものです。一方、相互作用効果は、3つ目の変数のレベルに依存して2つの変数間の関係が異なるかどうかを検定することを目的としています。

二要因分散分析を実行する際、相互作用効果を検定することは必須ではありません。ただし、相互作用効果が存在する場合、相互作用効果を省略すると誤った結論につながる可能性があります。

上記の例に戻ると、次の仮説検定があります：

性別による体重の主効果：

• H0：雌雄間の平均体重は同じです。
• H1：雌雄間の平均体重には差があります。

種による体重の主効果：

• H0：すべての3種の平均体重は同じです。
• H1：少なくとも1つの種の平均体重は異なります。

性別と種の相互作用：

• H0：性別と種の間には相互作用がなく、つまり、種と体重の関係は雌雄で同じです（同様に、性別と体重の関係はすべての3種で同じです）。
• H1：性別と種の間には相互作用があり、つまり、種と体重の関係は雌雄で異なります（同様に、性別と体重の関係は種に依存します）。

二要因分散分析の仮定

ほとんどの統計テストには、結果が有効であるためのいくつかの仮定が必要であり、二要因分散分析も例外ではありません。

二要因分散分析の仮定は、一要因分散分析と類似しています。要約すると：

• 変数の種類：従属変数は量的連続変数である必要があり、2つの独立変数はカテゴリー変数である必要があります（少なくとも2つのレベルを持つ）。
• 独立性：観測値はグループ間および各グループ内で独立している必要があります。
• 正規性：
• 小さなサンプルの場合、データは正規分布に近い必要があります。
• 大きなサンプルの場合（通常、各グループ/サンプルでn≥30）、正規性は必要ありません（中心極限定理のおかげで）。
• 分散の等質性：分散はグループ間で等しくなければなりません。
• 外れ値：どのグループにも有意な外れ値が存在してはいけません。

これらの仮定に関する詳細は、一要因分散分析の仮定についての記事で説明されています。

これで、二要因分散分析の基礎的な仮定を見てきました。テストを実行して結果を解釈する前に、データセットに特定の仮定が適用されるかどうかを確認します。

変数の種類

従属変数である体重は量的連続変数であり、独立変数である性別と種は質的変数（少なくとも2つのレベルを持つ）であるため、この仮定は満たされています。

独立性

独立性は、実験の設計とデータの収集方法に基づいて通常チェックされます。

簡単に言うと、観察値は通常、次のようになります。

• 独立: 各実験単位（ここではペンギン）が一度しか測定されず、観察値が集団の代表的かつランダムに選択された部分から収集された場合、または
• 依存: 各実験単位が少なくとも2回測定された場合（例えば医療分野では、同じ被験者に対して治療前と治療後の2回の測定が行われることがよくある）。

今回の場合、体重は各ペンギンについて一度だけ測定され、集団の代表的かつランダムなサンプルから収集されたため、独立性の仮定は満たされています。

正規性

全てのサブグループ（2つの要因のレベルの各組み合わせであるセル）において、大きなサンプルがあります:

table(dat$species, dat$sex)

##            ##             female male##   Adelie        73   73##   Chinstrap     34   34##   Gentoo        58   61

従って、正規性をチェックする必要はありません。

完全性のために、正規性を検証する方法を、サンプルが小さい場合を想定して、いくつか紹介します。

正規性の仮定をテストする方法はいくつかありますが、最も一般的な方法は:

• グループ別または残差に対してQQプロットを作成すること、および/または
• グループ別または残差に対してヒストグラムを作成すること、および/または
• グループ別または残差に対して正規性検定（例えばShapiro-Wilk検定）を行うこと

最も簡単で短い方法は、残差のQQプロットで正規性を検証することです。このプロットを描くには、まずモデルを保存する必要があります:

# モデルを保存するmod <- aov(body_mass_g ~ sex * species,  data = dat)

このコードの詳細は後ほど説明します。

これで、残差のQQプロットを描くことができます。2つの方法を示します。最初はplot()関数を使用したもので、次に{car}パッケージのqqPlot()関数を使用したものです:

# 方法1plot(mod, which = 2)

# 方法2library(car)

qqPlot(mod$residuals,  id = FALSE # ポイントの識別情報を削除)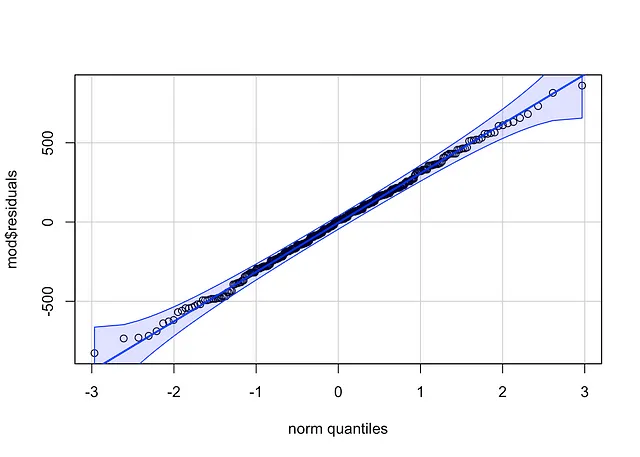

方法1のコードは少し短く、参照線の周りの信頼区間が抜けています。

ポイントが直線（Henryの線と呼ばれる）に沿っており、信頼帯内に収まっている場合、正規性を仮定できます。この場合、そのようになっています。

残差のヒストグラムで正規分布を確認する場合は、次のコードを使用します。

# ヒストグラムhist(mod$residuals)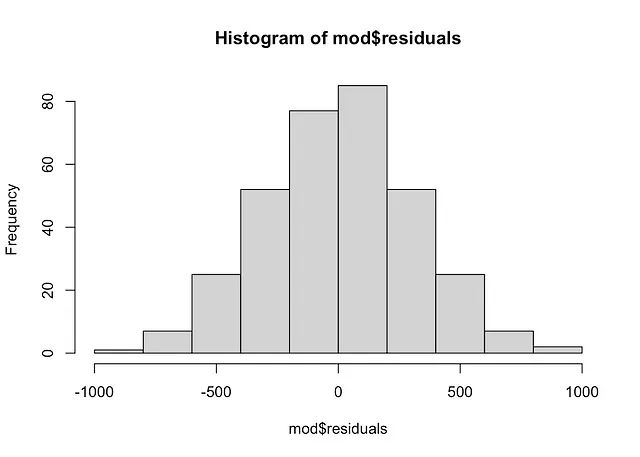

残差のヒストグラムは、ガウス分布を示しており、QQプロットの結論と一致しています。

QQプロットとヒストグラムが正規性を検証するのに十分であるにもかかわらず、より形式的な方法で正規性をテストする場合は、残差にShapiro-Wilk検定を適用することができます。

# 正規性検定shapiro.test(mod$residuals)

## ##  Shapiro-Wilk normality test## ## data:  mod$residuals## W = 0.99776, p-value = 0.9367

⇒残差が正規分布に従うという帰無仮説を棄却しない（p値=0.937）。

QQプロット、ヒストグラム、Shapiro-Wilk検定から、残差の正規性の帰無仮説を棄却しないと結論づけます。

正規性の仮定が確認されたので、分散の等質性を確認できます。2

分散の均一性

分散の等質性、または等分散性としても参照される分散の等質性は、plot()関数を使って視覚的に確認できます:

plot(mod, which = 3)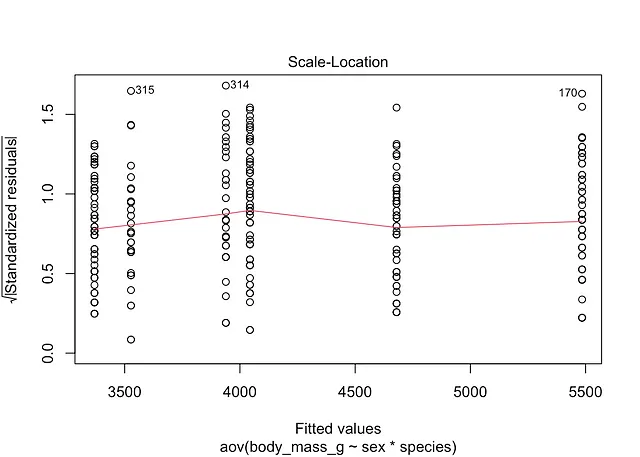

残差の散布が一定であるため、赤いスムーズな線が水平で平らであるため、ここでは一定分散の仮定が満たされているようです。

上記の診断プロットは十分ですが、Leveneのテスト（{car}パッケージから）でもより形式的にテストできます: 3

leveneTest(mod)

## Levene's Test for Homogeneity of Variance (center = median)##        Df F value Pr(>F)## group   5  1.3908 0.2272##       327

⇒分散が等しいという帰無仮説を棄却しません（p値=0.227）。

視覚的および形式的アプローチの両方が同じ結論を与えます。分散の等質性の仮定を棄却しないと判断します。

外れ値

外れ値を検出する最も簡単で一般的な方法は、グループごとの箱ひげ図による視覚的検出です。

女性と男性の場合:

library(ggplot2)

# boxplots by sexggplot(dat) +  aes(x = sex, y = body_mass_g) +  geom_boxplot()

3種類の場合:

# boxplots by speciesggplot(dat) +  aes(x = species, y = body_mass_g) +  geom_boxplot()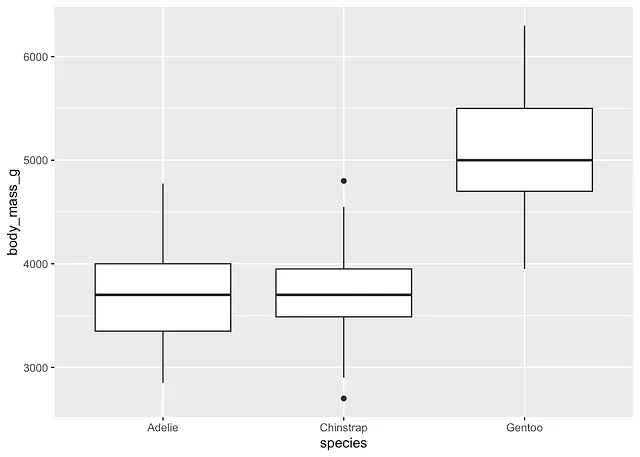

Chinstrapの種に対して、四分位範囲基準により、2つの外れ値が定義されています。 しかしながら、これらの点は結果に影響を与えるほど極端ではありません。

したがって、有意な外れ値の仮定がないと考えます。

二要因分散分析

すべての仮定が満たされていることを示したので、Rで二要因分散分析を実施することができます。

これにより、次の研究質問に答えることができます。

• 種を制御した場合、2つの性別間の体重は有意に異なりますか？
• 性別を制御した場合、少なくとも1つの種の体重は有意に異なりますか？
• ペンギンの種と体重の関係は、女性と男性で異なりますか？

予備分析

どの統計的検定も実行する前に、データの最初の概要を持つために、記述統計またはプロットを作成することが良い習慣です。

これは、記述統計またはプロットを介して実行できます。

記述統計

各サブグループの平均だけを計算する場合、簡単になります:

# mean by groupaggregate(body_mass_g ~ species + sex,  data = dat,  FUN = mean)

##     species    sex body_mass_g## 1    Adelie female    3368.836## 2 Chinstrap female    3527.206## 3    Gentoo female    4679.741## 4    Adelie   male    4043.493## 5 Chinstrap   male    3938.971## 6    Gentoo   male    5484.836

または、{dplyr}パッケージを使用して、各サブグループの平均と標準偏差を求めることもできます：

# mean and sd by grouplibrary(dplyr)

group_by(dat, sex, species) %>%  summarise(    mean = round(mean(body_mass_g, na.rm = TRUE)),    sd = round(sd(body_mass_g, na.rm = TRUE))  )

## # A tibble: 8 × 4## # Groups:   sex [3]##   sex    species    mean    sd##   <fct>  <fct>     <dbl> <dbl>## 1 女性 Adelie     3369   269## 2 女性 Chinstrap  3527   285## 3 女性 Gentoo     4680   282## 4 男性   Adelie     4043   347## 5 男性   Chinstrap  3939   362## 6 男性   Gentoo     5485   313## 7 <NA>   Adelie     3540   477## 8 <NA>   Gentoo     4588   338

プロット

ブログの常連読者であれば、テストの結果を解釈する前に、手元のデータを視覚化するためにプロットを描くのが好きだということを知っているでしょう。

量的変数と質的変数が2つある場合に最適なプロットは、グループ別の箱ひげ図です。これは、{ggplot2}パッケージを使用して簡単に作成できます：

# boxplot by grouplibrary(ggplot2)

ggplot(dat) +  aes(x = species, y = body_mass_g, fill = sex) +  geom_boxplot()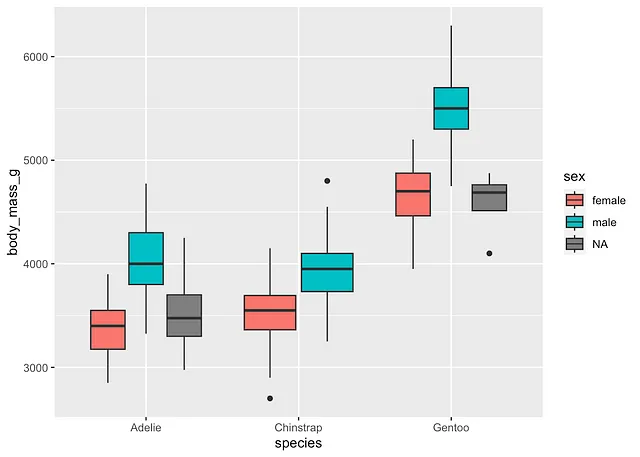

一部の観測値には性別が欠落しているため、より簡潔なプロットを作成するためにそれらを削除できます：

dat %>%  filter(!is.na(sex)) %>%  ggplot() +  aes(x = species, y = body_mass_g, fill = sex) +  geom_boxplot()

注意すべきは、次のようなプロットも作成できることです：

dat %>%  filter(!is.na(sex)) %>%  ggplot() +  aes(x = sex, y = body_mass_g, fill = species) +  geom_boxplot()

しかし、より読みやすいプロットの場合、カテゴリ数が最小である変数を色（実際にはaes()レイヤーの引数fill）に、カテゴリ数が最大である変数をx軸（すなわちaes()レイヤーの引数x）に配置することを好む傾向があります。

サブグループごとの平均値と箱ひげ図から、サンプル内では：

• 女性のペンギンの体重は男性よりも低く、すべての考慮された種に当てはまり、
• 体重はジェントー・ペンギンの方が他の2種よりも高い。

これらの結論は、サンプル内に限定されるものであることに注意してください！これらの結論を一般化するには、2要因の分散分析を実行し、説明変数の有意性を確認する必要があります。これが次のセクションの目的です。

Rにおける2要因分散分析

前述のように、2要因分散分析に相互作用効果を含めることは必須ではありません。しかし、誤った結論を避けるために、まず相互作用が有意かどうかを確認し、その結果に基づいてそれを含めるかどうかを決定することをお勧めします。

交互作用が有意でない場合、最終モデルからそれを削除しても安全です。逆に、交互作用が有意である場合、結果を解釈するために使用される最終モデルに含める必要があります。

したがって、主効果（つまり、性別と種）と交互作用を含むモデルから始めます：

# 交互作用を伴う二元分散分析# モデルの保存mod <- aov(body_mass_g ~ sex * species,  data = dat)

# 結果の表示summary(mod)

##              Df    Sum Sq  Mean Sq F value   Pr(>F)    ## sex           1  38878897 38878897 406.145  < 2e-16 ***## species       2 143401584 71700792 749.016  < 2e-16 ***## sex:species   2   1676557   838278   8.757 0.000197 ***## Residuals   327  31302628    95727                     ## ---## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## 11 observations deleted due to missingness

（列Sum Sqの）平方和は、種が体重の変動の大部分を説明していることを示しています。これは、この変動を説明するために最も重要な要因です。

p値は、出力の最後の列（Pr(>F)）に表示されます。これらのp値から、5％の有意水準で、以下のことが結論付けられます：

• 種を制御している場合、体重は2つの性別間で有意に異なります。
• 性別を制御している場合、少なくとも1つの種について体重が有意に異なります。
• 性別と種の交互作用（上記出力のsex:speciesの行に表示される）が有意である。

したがって、有意な交互作用効果から、体重と種の関係はメスとオスで異なることがわかります。有意であるため、このモデルを保持し、そのモデルから結果を解釈する必要があります。

逆に、交互作用が有意でなかった場合（つまり、p値≥0.05の場合）、この交互作用効果をモデルから削除しました。説明のために、交互作用を含まない二元分散分析（加算モデルと呼ばれる）のコードを以下に示します：

# 交互作用を含まない二元分散分析aov(body_mass_g ~ sex + species,  data = dat)

Rで線形回帰を実行することに慣れている読者にとっては、二元分散分析のコードの構造が実際には似ていることに気付くでしょう：

• 式は従属変数〜独立変数です。
• 独立変数を交互作用なしで含めるには、+記号が使用されます。
• 独立変数を交互作用を含めて含めるには、*記号が使用されます。

二元分散分析は、すべての分散分析と同様に、実際には線形モデルであるため、線形回帰との類似性は驚くべきものではありません。

以下のコードでも機能することに注意してください。同じ結果が得られます：

# 方法2mod2 <- lm(body_mass_g ~ sex * species,  data = dat)

Anova(mod2)

## Anova Table (Type II tests)## ## Response: body_mass_g##                Sum Sq  Df F value    Pr(>F)    ## sex          37090262   1 387.460 < 2.2e-16 ***## species     143401584   2 749.016 < 2.2e-16 ***## sex:species   1676557   2   8.757 0.0001973 ***## Residuals    31302628 327                      ## ---## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

aov()関数は、独立グループ化変数の各レベルで等しいサンプルサイズがあるバランスの取れた設計を前提としています。

バランスの取れていない設計（つまり、各サブグループに不均等な数の被験者がいる場合）の場合、推奨される方法は次のとおりです：

• タイプII ANOVAが相互作用がない場合、RでAnova(mod, type = "II")を使用して実行できます。5、そして
• 相互作用がある場合のタイプIII ANOVAは、RでAnova(mod, type = "III")を使用して実行できます。

これは投稿の範囲を超えており、ここではバランスの取れた設計を前提としています。興味のある読者は、タイプI、タイプII、タイプIII ANOVAに関するこの詳細な議論を参照してください。

ペアワイズ比較

2つの主効果が有意であることから、次のことが結論づけられます：

• 種を制御する場合、メスとオスの体重は異なり、
• 性別を制御する場合、体重は少なくとも1つの種で異なる。

2つの性別間で体重に違いがある場合、ちょうど2つの性別があるため、オスとメスの間で体重が有意に異なるということになります。

どちらの性別が最も体重があるか知りたい場合は、各サブグループごとの平均値やボックスプロットから推測できます。ここでは、オスがメスよりも有意に体重が大きいことが明らかになっています。

しかし、種に関してはそれほど簡単ではありません。なぜなら、性別とは異なり、3つの種（アデリー、チンストラップ、ジェントー）があるため、3つの種のペアがあるからです：

1. アデリーとチンストラップ
2. アデリーとジェントー
3. チンストラップとジェントー

少なくとも1つの種で体重が有意に異なる場合、次のようになる可能性があります：

• 体重がアデリーとチンストラップの間で有意に異なり、アデリーとジェントーの間で有意に異ならず、チンストラップとジェントーの間でも有意に異ならない、または
• 体重がアデリーとジェントーの間で有意に異なり、アデリーとチンストラップの間で有意に異ならず、チンストラップとジェントーの間でも有意に異ならない、または
• 体重がチンストラップとジェントーの間で有意に異なり、アデリーとチンストラップの間で有意に異ならず、アデリーとジェントーの間でも有意に異ならない。

また、次のようになる可能性もあります：

• 体重がアデリーとチンストラップの間、アデリーとジェントーの間で有意に異なり、チンストラップとジェントーの間では有意に異ならない、または
• 体重がアデリーとチンストラップの間、チンストラップとジェントーの間で有意に異なり、アデリーとジェントーの間では有意に異ならない、または
• 体重がチンストラップとジェントーの間、アデリーとジェントーの間で有意に異なり、アデリーとチンストラップの間では有意に異ならない。

最後に、体重がすべての種で有意に異なる場合もあります。

1要因のANOVAと同様に、この段階では、体重に関してどの種がどの種と異なるかを正確には知ることができません。これを知るには、事後検定（またはペアワイズ比較とも呼ばれる）を使用して、各種を2つずつ比較する必要があります。

いくつかの事後検定がありますが、最も一般的なものはTukey HSDで、すべての可能なグループのペアをテストします。先に述べたように、このテストは、性別には2つのレベルしかないため、種変数でのみ実行する必要があります。

1要因のANOVAと同様に、Tukey HSDはRで次のように実行できます：

# method 1TukeyHSD(mod,  which = "species")

##   Tukey multiple comparisons of means##     95% family-wise confidence level## ## Fit: aov(formula = body_mass_g ~ sex * species, data = dat)## ## $species##                        diff       lwr       upr     p adj## Chinstrap-Adelie   26.92385  -80.0258  133.8735 0.8241288## Gentoo-Adelie    1377.65816 1287.6926 1467.6237 0.0000000## Gentoo-Chinstrap 1350.73431 1239.9964 1461.4722 0.0000000

または、{multcomp}パッケージを使用することもできます:

# 方法2library(multcomp)

summary(glht(  aov(body_mass_g ~ sex + species,    data = dat  ),  linfct = mcp(species = "Tukey")))

## ##   Simultaneous Tests for General Linear Hypotheses## ## Multiple Comparisons of Means: Tukey Contrasts## ## ## Fit: aov(formula = body_mass_g ~ sex + species, data = dat)## ## Linear Hypotheses:##                         Estimate Std. Error t value Pr(>|t|)    ## Chinstrap - Adelie == 0    26.92      46.48   0.579     0.83    ## Gentoo - Adelie == 0     1377.86      39.10  35.236   <1e-05 ***## Gentoo - Chinstrap == 0  1350.93      48.13  28.067   <1e-05 ***## ---## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1## (Adjusted p values reported -- single-step method)

または、お好みのp値調整方法を使用してpairwise.t.test()関数を使用することもできます:6

# 方法3pairwise.t.test(dat$body_mass_g, dat$species,  p.adjust.method = "BH")

## ##  Pairwise comparisons using t tests with pooled SD ## ## data:  dat$body_mass_g and dat$species ## ##           Adelie Chinstrap## Chinstrap 0.63   -        ## Gentoo    <2e-16 <2e-16   ## ## P value adjustment method: BH

2番目の方法を使用する場合、相互作用が有意であっても、glht()関数に指定する必要があるのは相互作用のないモデルです。また、自分のモデルの名前と独立変数の名前を私のコードのmodとspeciesに置き換えることを忘れないでください。

両方の方法で同じ結果が得られます:

• チンストラップとアデリーペンギンの体重には有意差はありません（調整済みp値=0.83）
• ジェンツーペンギンとアデリーペンギンの体重には有意な差があります（調整済みp値<0.001）
• ジェンツーペンギンとチンストラップの体重には有意な差があります（調整済みp値<0.001）

複数のグループのペアを比較する際に発生する多重検定の問題を防ぐため、報告されるのは調整済みp値です。

すべてのグループの組み合わせを比較したい場合は、TukeyHSD()関数を使用して、which引数で相互作用を指定します:

# 全ての性別と種類の組み合わせTukeyHSD(mod,  which = "sex:species")

##   Tukey multiple comparisons of means##     95% family-wise confidence level## ## Fit: aov(formula = body_mass_g ~ sex * species, data = dat)## ## $`sex:species`##                                      diff       lwr       upr     p adj## male:Adelie-female:Adelie        674.6575  527.8486  821.4664 0.0000000## female:Chinstrap-female:Adelie   158.3703  -25.7874  342.5279 0.1376213## male:Chinstrap-female:Adelie     570.1350  385.9773  754.2926 0.0000000## female:Gentoo-female:Adelie     1310.9058 1154.8934 1466.9181 0.0000000## male:Gentoo-female:Adelie       2116.0004 1962.1408 2269.8601 0.0000000## female:Chinstrap-male:Adelie    -516.2873 -700.4449 -332.1296 0.0000000## male:Chinstrap-male:Adelie      -104.5226 -288.6802   79.6351 0.5812048## female:Gentoo-male:Adelie        636.2482  480.2359  792.2606 0.0000000## male:Gentoo-male:Adelie         1441.3429 1287.4832 1595.2026 0.0000000## male:Chinstrap-female:Chinstrap  411.7647  196.6479  626.8815 0.0000012## female:Gentoo-female:Chinstrap  1152.5355  960.9603 1344.1107 0.0000000## male:Gentoo-female:Chinstrap    1957.6302 1767.8040 2147.4564 0.0000000## female:Gentoo-male:Chinstrap     740.7708  549.1956  932.3460 0.0000000## male:Gentoo-male:Chinstrap      1545.8655 1356.0392 1735.6917 0.0000000## male:Gentoo-female:Gentoo        805.0947  642.4300  967.7594 0.0000000

{agricolae} パッケージの HSD.test() 関数を使用することもできます。この関数は、同じ文字で表される差が有意ではないサブグループを示します。

library(agricolae)

HSD.test(mod,  trt = c("sex", "species"),  console = TRUE # 結果を表示)

## ## Study: mod ~ c("sex", "species")## ## HSD Test for body_mass_g ## ## Mean Square Error:  95726.69 ## ## sex:species,  means## ##                  body_mass_g      std  r  Min  Max## female:Adelie       3368.836 269.3801 73 2850 3900## female:Chinstrap    3527.206 285.3339 34 2700 4150## female:Gentoo       4679.741 281.5783 58 3950 5200## male:Adelie         4043.493 346.8116 73 3325 4775## male:Chinstrap      3938.971 362.1376 34 3250 4800## male:Gentoo         5484.836 313.1586 61 4750 6300## ## Alpha: 0.05 ; DF Error: 327 ## Critical Value of Studentized Range: 4.054126 ## ## Groups according to probability of means differences and alpha level( 0.05 )## ## Treatments with the same letter are not significantly different.## ##                  body_mass_g groups## male:Gentoo         5484.836      a## female:Gentoo       4679.741      b## male:Adelie         4043.493      c## male:Chinstrap      3938.971      c## female:Chinstrap    3527.206      d## female:Adelie       3368.836      d

多数のグループを比較する場合、プロットすることがより解釈しやすくなるかもしれません。

# ラベルが切り捨てられないように軸の余白を設定しますpar(mar = c(4.1, 13.5, 4.1, 2.1))

# 各比較の信頼区間を作成しますplot(TukeyHSD(mod, which = "sex:species"),  las = 2 # x軸の目盛りを回転させます)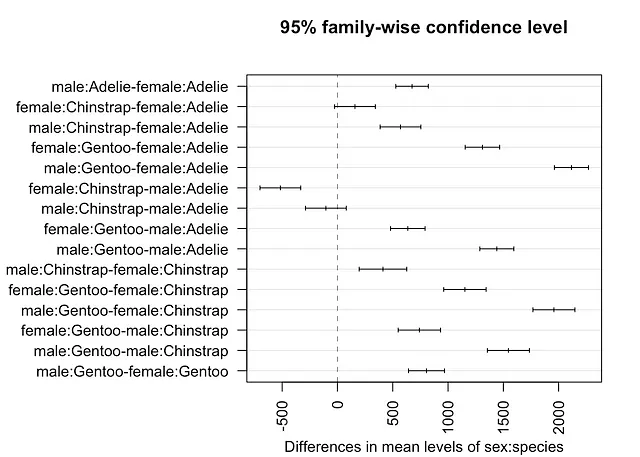

上記の出力とプロットから、すべての性別と種の組み合わせは有意に異なることがわかります。ただし、女性チンストラップと女性アデリーペンギン（p値=0.138）および男性チンストラップと男性アデリーペンギン（p値=0.581）の間には有意な差がありません。

これらの結果は、前述のボックスプロットと一致し、以下に示す視覚化で確認されます。

Rにおける二因子分散分析は以上のように終了します。

視覚化

予備分析で既に提示されたものとは異なる方法で結果を視覚化する場合は、以下に有用なプロットのアイデアがいくつかあります。

まず、{effects} パッケージの allEffects() 関数を使用して、サブグループごとの平均値と平均誤差を使用してプロットすることができます。

# 方法1library(effects)

plot(allEffects(mod))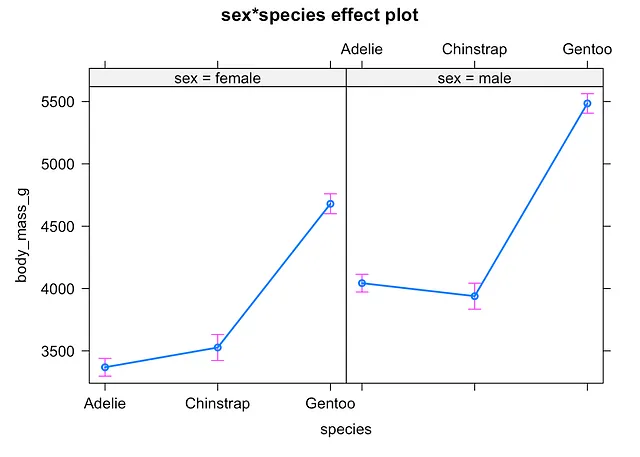

または、{ggpubr} パッケージを使用することもできます。

# 方法2library(ggpubr)

ggline(subset(dat, !is.na(sex)), # sexのNAレベルを削除します  x = "species",  y = "body_mass_g",  color = "sex",  add = c("mean_se") # 平均値と標準誤差を追加) +  labs(y = "Mean of body mass (g)")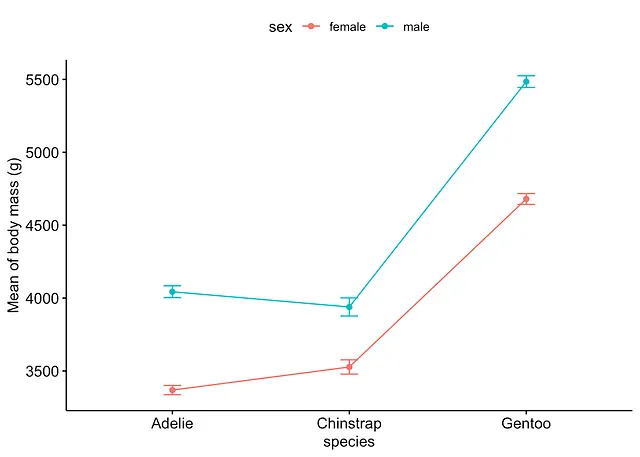

または、{Rmisc} および {ggplot2} を使用する場合：

library(Rmisc)

# サブグループごとの平均と標準誤差を計算summary_stat <- summarySE(dat,  measurevar = "body_mass_g",  groupvars = c("species", "sex"))# 平均と標準誤差をプロットggplot(  subset(summary_stat, !is.na(sex)), # sex の NA レベルを削除  aes(x = species, y = body_mass_g, colour = sex)) +  geom_errorbar(aes(ymin = body_mass_g - se, ymax = body_mass_g + se), # エラーバーを追加    width = 0.1 # エラーバーの幅  ) +  geom_point() +  labs(y = "体重の平均 (g)")

次に、サブグループごとに平均値のみを描画する場合：

with(  dat,  interaction.plot(species, sex, body_mass_g))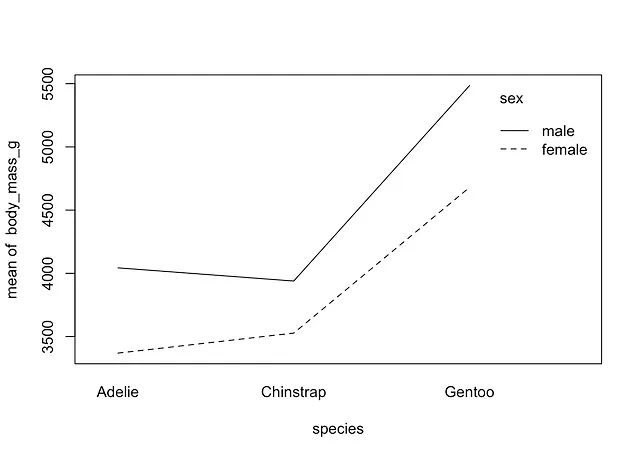

最後に、GraphPad に慣れ親しんでいる方々には、平均とエラーバーを以下のようにプロットする方法がおなじみかもしれません：

# 平均と標準誤差をバープロットとしてプロットsggplot(  subset(summary_stat, !is.na(sex)), # sex の NA レベルを削除  aes(x = species, y = body_mass_g, fill = sex)) +  geom_bar(position = position_dodge(), stat = "identity") +  geom_errorbar(aes(ymin = body_mass_g - se, ymax = body_mass_g + se), # エラーバーを追加    width = 0.25, # エラーバーの幅    position = position_dodge(.9)  ) +  labs(y = "体重の平均 (g)")

結論

この記事では、異なるグループ間で定量的変数を比較するために存在する異なる検定についてのいくつかのリマインダーから始め、2要因分散分析に焦点を当て、目標と仮説から R における実装、解釈、およびいくつかの視覚化までを説明しました。また、等分散性の仮定とすべてのサブグループを比較するための事後検定についても簡単に言及しました。

これらは、{palmerpenguins} パッケージから入手できる penguins データセットで説明されました。

読んでいただきありがとうございます。

この記事がデータを使用した2要因分散分析の実行に役立つことを願っています。

いつものように、この記事で取り上げたトピックに関する質問や提案がある場合は、コメントに追加して他の読者が議論から利益を得ることができるようにしてください。

1. 理論的には、1要因分散分析は2つのグループを比較するためにも使用できますが、3つ以上のグループを比較するためには1要因分散分析がしばしば行われます。独立したサンプルの Student の t 検定と2つのグループの1要因分散分析によって得られる結論は類似しています。 ↩︎
2. 正規性の仮定が満たされない場合は、多くの変換が適用されることがあります。最も一般的なものは対数変換（ R では log() 関数）です。 ↩︎
3. Bartlett の検定も等分散性の仮定を検定するのに適しています。 ↩︎
4. 加法モデルは、2つの説明変数が独立であることを前提としています。それらは互いに相互作用しません。 ↩︎
5. ここで、mod は保存されたモデルの名前です。 ↩︎
6. ここでは、Benjamini & Hochberg (1995) の修正を使用していますが、いくつかの方法から選択できます。詳細については、?p.adjust を参照してください。 ↩︎

関連記事

• RにおけるANOVA
• Rにおける学生のt検定と手計算：異なるシナリオ下で2つのグループを比較する方法は？
• Rにおける1標本Wilcoxon検定
• Kruskal-Wallis検定、あるいはANOVAのノンパラメトリックバージョン
• 手計算による仮説検定

元の記事は2023年6月19日にhttps://statsandr.comで公開されました。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!