「二つの封筒の問題」

Two envelope problem

パラドックスシリーズ #1

時間と因果関係がランダム性から現れる方法

2つの封筒問題は、直感的ながらも誤ったベイジアン確率推定を使用して最善の行動を決定する際に、逆説的で一貫性のない決定が生じます。数学的な間違いを修正するのは簡単ですが、それ以上のことがあります。まず、問題をわずかに変更することで、未決定にすることができます。これは、言語の曖昧さと数学的形式主義とは対照的な例です。第二に、複数の可能な解を比較すると、数学的な世界で時間が現れており、因果関係の仮説をテストすることが理論的に可能です。

2つの封筒問題（TEP）

テーブルの上に同じように見える2つの封筒を見せ、両方がお金を含んでいること（嘘をつかないで）と伝え、そのうちの1つを選んで中のお金を自分で保持するように提案します。

一度選んだ後、開ける前にもう一方の封筒に変更したいかどうか尋ねます。

あなたはどうしますか？

• Python Enumerate（）：カウンターを使用してループを簡素化する
• 「エキサイティングなローンチ：無料のGenAI Nanoコースを発表します」
• Pythonにおけるオブジェクト指向プログラミング（OOP）- 初心者向け（パート1）

おそらく、封筒を交換することは無駄だと言うでしょう。なぜなら、どちらの封筒を選んでも状況は同じだからです。しかし、あなたが未知の金額xを選んだこと、そしてもう片方の封筒には2xまたはx/2の金額yが等しい確率で含まれていることに注意する必要があります。したがって、期待される金額yは2x (1/2) + x/2 (1/2) = 5x/4であり、xよりも大きいです。だから、おそらくそれでも交換するべきです。

もちろん、yに基づいて期待される金額xも計算することができます。yが2yまたはy/2のいずれかの確率が半々であるため、期待される金額xは5y/4であり、yよりも大きいです。

では、この計算には何が問題なのでしょうか？どちらの封筒が他よりも多くのお金を含んでいる可能性が高いのでしょうか？

推論の数学的な欠陥

私たちは恣意的に1つの封筒を「X」とラベル付けし、もう1つを「Y」とラベル付けします。今度は、Y封筒に観測された金額yを知っている場合のX封筒の条件付き期待値を適切に計算します。

Y = yの条件のもとでX封筒の金額の期待値、E[X|Y = y]を正しく計算するためには、明らかに観測された特定の金額yに依存します。yのすべての可能な値に対して、Xの金額xはy/2または2yのいずれかである確率が1/2であるため、特定の値のyについても同じであるということではありません。例えば、yが「非常に小さい」という意味で（後で明確にされる意味で）、xがyよりも大きい確率が高く、yが「非常に大きい」という場合、xがyよりも小さい確率が高くなります。yのすべての可能な値に対して確率がバランスされることで、Xが半分の時間Yの半分であり、もう半分の時間Yの2倍であることがありますが、P(X = y/2|Y = y) = 1/2およびP(X = 2y|Y = y) = 1/2というわけではありません。ただし、P(X = Y/2) = P(X = 2Y) = 1/2であるということだけです。

したがって、E[X|Y = y]を正しく計算しようとする必要がありますが、まずUおよびZのランダムな数値がどのように選択されたのかを明確にする必要があります。最初の封筒にはランダムな金額Uを入れ、2Uの金額を2番目の封筒に入れました。それからシャッフルし、封筒の1つをXと名付け、もう1つをYと名付けました。この名前のプロセスを次のように表すことができます。2進数の数値Zを抽選します（0または1の確率が半々です）。Z = 0の場合、XにはUが入った封筒であり、それ以外の場合（Z = 1の場合）は金額2Uの封筒です。

これにより、UおよびZのランダムな数値がどのように選択されたかを知らない外部の観察者からは、封筒の金額は次のように見えます：

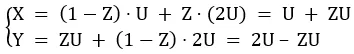
私たちは、P(X = 2Y) = P(U + ZU = 4U – 2ZU) = P(3U – 3ZU = 0) = P(U=ZU) = P(Z = 1) = 1/2 (そして、P(X = Y/2)についても同じです)を検証できます。

今、私たちは正しくE[X|Y = y] = E[3U-Y|Y = y] = E[3U|Y = y] – E[Y|Y = y] = 3E[U|Y = y] — yを計算できます。

まだE[U|Y = y]を計算する必要があります。これにはP(U=u|Y=y)を知る必要がありますが、これは（ベイズの定理から）P(Y=y|U=u)P(U=u)に比例します。

P(Y = y|U)を計算するために、YはUまたは2Uのいずれかであることを思い出します。したがって、Uが取る値uはyまたはy/2です：

• yがuまたはu/2でない場合、Y = yの確率はありません：P(Y = y|U = u) = 0
• yがuの場合、Y = yの確率は1/2です（Z = 1の確率）：P(Y = y|U = u) = 1/2
• yがu/2の場合、Y = yの確率は1/2です（Z = 0の確率）：P(Y = y|U = u) = 1/2

数学的な形式では：

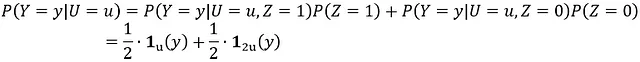
ここで：

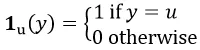
これらすべてをまとめると：

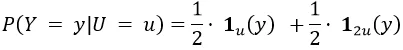
次に、P(U = u)を知る必要があります。仮定をするしかありませんが、例えばUは正の実数上で指数分布（パラメータλ>0）に従うと仮定できます：

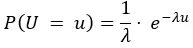
最終的には、P(U = u|Y = y)は次のように比例します：

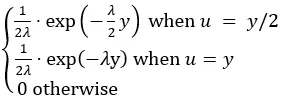
言い換えれば：

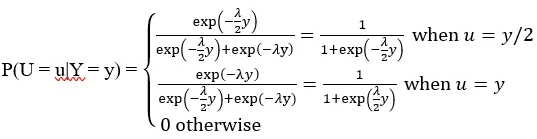
これで、E[X|Y = y] = 3E[U|Y = y] — yを計算するために必要なすべてを持っています。つまり：

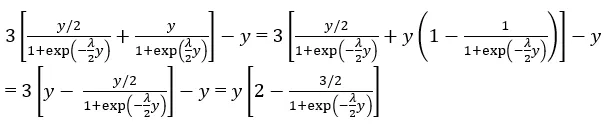
要約すると、私たちは今、次のことを知っています：

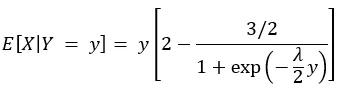
これは最初の5y/4とはかなり異なります！

xの期待値は、厳密にはyよりも大きい場合にのみyです：

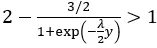
または、言い換えれば：

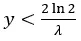
（これは、金額が引かれるパラメータλの指数分布の中央値の2倍です）。

したがって、以前の推論のエラーをより良く理解することができます。すべての可能な値yについて平均化すると、Xがyの倍の金額である時間の半分と、同じ金額の半分である時間の半分であることは真実ですが、yの特定の値に対して確率は半分ではありません：yが値Uが選択された方法から期待されるものと比べて「大きい」場合、封筒Xにより小さい金額が含まれる確率が高くなり、yが「小さい」場合、封筒Xにより大きな金額が含まれる確率が高くなります。ここでは、「大きい」と「小さい」の境界は単に指数分布の中央値の2倍です。

XまたはYの選択は対称的であり、E[Y|X = x] = E[3U — X|X = x] = 3E[U|X=x] – xとなり、ここからすべての前の計算が適用されます。

パラドックスが解決されたように思われますが、実際には2つの封筒の問題は決定不能であり、問題が対称的であるか、あるいは一方の封筒を他方よりも好むべきかどうかを本当に知ることができません。

決定不能な問題

さて、テーブルの上には「X」と「Y」というラベルが付いた2つの見た目が同じ封筒が置かれています。今、封筒Xには封筒Yの半分の金額か、その金額の2倍が等しい確率で含まれていると言われました。対称性から、封筒Yにも同じことが当てはまります。これから、1つの封筒を選ぶように求められます。どちらを選ぶべきですか？

前の例に基づくと、どちらかを選んでも同じだと思われます。しかし、これは間違っています！すべては私たちの仮説に依存します。言い換えれば、（統計的な）問題の表現に依存します。

ここで、封筒を選ぶ際に既にラベルが付いているという事実が重要です。封筒内の金額を選ぶプロセスとラベルを付けるためのプロセスは何でしょうか？前の例で行われたように、それらがランダムにラベル付けされた場合、どちらかを選ぶことは統計的に同等であると同意します。

しかし、Xの金額は正の実数上の指数分布（パラメータλ>0）から選択されると想像してみてください。前の例でUに対して行ったのと同様に。その後、封筒Yの金額は単に封筒Y内の金額の半分または2倍がランダムに選択されます（均等な確率で）：Y = HX、ここでHは1/2または2の値を取り、それぞれ半分の確率で（HはXとは独立しています）。

ここで、Yの値の累積分布を計算しましょう：P(Y < y) = P(HX < y) = P(HX < y |H = 1/2) P(H = 1/2) + P(HX < y |H = 2) P(H = 2)

= P(X/2 < y) (1/2) + P(2X < y) (1/2) = (1/2) P(X < 2y) + (1/2) P(X < y/2)

= (1/2) F(2y) + (1/2) F(y/2)、ここでFはXの累積分布関数（指数分布）です

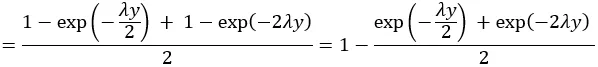
非負の値yに対して。

確率密度を得るために微分すると、Y = yの確率密度関数の平均を得ます：

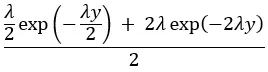
これは、パラメータλ/2の指数分布とパラメータ2λの指数分布の2つの確率密度関数の平均であり、封筒Yの平均値は2/λと1/(2λ)の平均です：

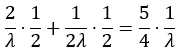
これは、パラメータλを持つ指数分布の平均値Xの平均値を超えるものであり、期待値の計算に興味がある場合、E[Y] = E[HX] = E[H] E[X]としてHとXは独立しているため、E[Y] = [(1/2)(1/2) + 2(1/2)] E[X] = (5/4)E[X]です。

結論として、この場合、平均値だけを考慮して決定を行う場合、常に封筒Yを選ぶべきです。

ただし、Y = HXではなく、X = HYと仮定することもできます。Yの金額はパラメータλの指数分布から引かれ、その場合は封筒Xを選ぶべきです。

テーブルに置かれた2つの封筒を生成したプロセスについて、追加の仮定なしでどの封筒を選ぶべきかを決定するには、十分な知識がありません。

これで全てですか？いいえ、最も興味深いことはこれからです。私たちは封筒を持つ状況を生成するための物理的なプロセスをランダム変数でモデル化する必要があることが、これまでの結果からわかります。

しかし、物理的なプロセスには時間があります。例えば、Xの金額を選び、それからYに入れるべき金額を推測します。またはその逆です。そして、統計モデルはそれを再現することができます。Xの金額がYの金額よりも前に選ばれるか、後に選ばれるかによって、異なる結論が導かれます。言い換えれば、私たちの統計モデルは、時間の物理的な現実を数学的に再現することができます。

ランダム性からの時間と因果関係の出現

数学は相関関係のみを証明できるとよく言われますが、因果関係は証明できません。その点で、計量経済学における因果関係分析は、数学が関与する限り相関分析にすぎません。イベントが他のイベントの結果であると人間の思考が判断するのは、両方のイベント間の相関と時間に基づきます。最初のイベントの後に発生するイベントは結果に過ぎず、原因ではないということです。

時間は数学的な概念ではなく、物理的な概念です。数学は、何が最初に起こった現象（したがって原因とされる）であり、何が次に起こった現象（したがって結果とされる）であるかについて、人間の入力に依存せずに因果関係を確立するのには無力であるように思われます。しかし、本当にそうなのでしょうか？時間の概念は不可逆性の概念に由来します。物体が左から右に移動するとき、それは時間の変化ではなく、物体は元の位置に戻ることができるからです。物体が年を取るとき、それは時間の経過による変化です。なぜなら、このプロセスは不可逆的だからです。時間は世界の状態の不可逆的な変化です。

物理学では、不可逆性は、形式的にはエントロピーと呼ばれる無秩序の増加の結果として見られます。物体を構成する分子がより無秩序になるため、物体は元の状態に戻ることができなくなり、変化は時間によってだけでなく、時間のために起こると見なされます。状態の変化が時間の経過を示しているだけであれば、時間が経過していると言えますが、物理的な不可逆性によって時間は一方向にのみ流れ、原因と結果を区別することができるようになります。

詳細には立ち入らずに、老化した物体のマクロ状態だけが不可逆です。微視的なレベルでは、理論物理学の視点からは、分子や粒子は過去の状態に似た方法で自己整序することができます。したがって、物理的な不可逆性は、非可逆的な数学的関数によって単純にモデル化することはできません。代わりに、ランダム変数はマクロ的には非可逆ですが、微視的には可逆です。例えば、Y = HXであれば、X = Y/Hとは限りません（マクロ的な観点からの不可逆性）。しかし、Y、H、Xが取る値に関係なく、y = hxおよびx = y/h（微視的な観点からの可逆性）です。2つの封筒のパラドックスは特に混乱を引き起こします。その定義では、すべてが対称的に見えますが（xがyの半分または2倍である場合、yはxの2倍または半分であることを意味します）、これは「微視的」レベルでのみ真実です。

物理的エントロピーとランダム変数の関連が因果関係の研究にどのように役立つのでしょうか？

2つの事前にラベル付けされた封筒XとYの最後の例を再考し、Y = HXまたはX = HYであることを知っていると仮定しましょう。それぞれの仮説をテストするために、XとYの大量の観測値を取ることができます。これにより、これら2つのランダム変数の確率密度関数を特定し、1つは他のランダム変数の密度に基づいて「エントロピック」な密度（特定の数学的関係に基づいて「エントロピック」）を持つことができますが、ランダム変数H（その密度は既知と仮定されている）によって「無秩序」にされます。

さて、より一般的な問題について考えてみましょう。しばしば、複数の変数間の因果関係を定量化するために線形回帰が行われます。例えば、Y = αXのようにYがXの結果であると仮定し、因果関係係数αを定量化したいとします。しかし、これはXからYへの因果関係を何ら証明するものではなく、仮定が真実である場合にのみXとYの関係性を定量化することができます。

YがαXと等しいと仮定されるこのような単純な例では、数学的に因果関係を特定することはできません。なぜなら、それはX = Y/αと言うことと等価であるからです。しかし、係数αがより一般的なプロセスAの1つの歴史的な値と考えられる場合、Y、A、Xの分布を比較し、Y = AXまたはX = Y/Aのどちらがより妥当かを判断することができます。別の例として、Z = X + Y（ZはXとYによって引き起こされる）という関係を、Y = Z – X（YはXとZによって引き起こされる）などの他の可能性と比較することができます。X、Y、Zの分布の比較によって因果関係の問題に答えることができます。

このような考察は非常に理論的であり、ランダム変数の分布を適切に推定することが費用がかかる、複雑な、または実現不可能な現実の生活で直接役立つものではありませんが、集約を使用して因果関係の分析を行うことを想像することができます。例えば、Y = HXとX = HYの間で選択しなければならない場合、最初の場合ではE[Y] > E[X]、2番目の場合ではE[X] > E[Y]であることがわかりました。線形関係の場合、X = Y + Z、Y = X – Z、Z = X – Yの間でテストする必要があるかもしれませんが、期待値は有用ではありません（指数関数を取る場合を除く、例えばexp(X)=exp(Y)exp(Z)）。なぜなら、E[X]はどの場合でもE[Y] + E[Z]に等しいからですが、関係Var(X) = Var(Y) + Var(Z) + 2Cov(Y, Z)は最初の場合にのみ真であるからです。

このような技術は因果関係について有用な示唆を提供し、仮説の検証に役立ちます。しかし、さらに重要なことは、物理的な時間が数学的な世界からランダム性の概念から現れることではないでしょうか？

結論

よく知られた統計学の「パラドックス」である二つの封筒問題を分析することから始め、問題の素朴な解法に数学的な欠陥があるだけでなく、人間の言語には二つの異なるランダム変数の関数（HXとX/H）が等価であるように見えるあいまいさがあることに気付きました。

更に掘り下げると、ランダム変数を含む方程式は一般的な場合（マクロ的視点）では「逆」にはできませんが、ランダム変数の実現を考慮すると（ミクロ的視点）、方程式は「逆」にできることがわかりました。

これは、ランダム変数の標本空間Ωと物理システムの位相空間の類似性を提案する機会であり、それによって統計世界における「物理エントロピー」および不可逆性と時間の出現を観察することができました。

最後に、暗い計算から時間が現れた後、単純な相関分析を超えて因果関係の仮説を検証する方法について結論を導くことができました。これが二つの封筒から得られたすべてです！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!