「トランスフォーマーベースのエンコーダーデコーダーモデル」

Transformer-based encoder-decoder model

!pip install transformers==4.2.1
!pip install sentencepiece==0.1.95

トランスフォーマーベースのエンコーダーデコーダーモデルは、Vaswani et al.によって有名なAttention is all you need論文で紹介され、現在では自然言語処理（NLP）におけるデファクトスタンダードのエンコーダーデコーダーアーキテクチャです。

最近、T5、Bart、Pegasus、ProphetNet、Margeなど、トランスフォーマーベースのエンコーダーデコーダーモデルの異なる事前学習目的に関する多くの研究が行われていますが、モデルのアーキテクチャはほとんど変わっていません。

このブログ記事の目的は、トランスフォーマーベースのエンコーダーデコーダーアーキテクチャがシーケンス対シーケンスの問題をどのようにモデル化しているかを詳細に説明することです。アーキテクチャによって定義された数学モデルとそのモデルを推論に使用する方法に焦点を当てます。途中で、NLPのシーケンス対シーケンスモデルについての背景をいくつか説明し、トランスフォーマーベースのエンコーダーとデコーダーのパーツに分解します。多くのイラストを提供し、トランスフォーマーベースのエンコーダーデコーダーモデルの理論と🤗Transformersにおける実際の使用方法のリンクを確立します。なお、このブログ記事ではそのようなモデルをトレーニングする方法については説明していません。これについては将来のブログ記事のテーマです。

• 「ODSC Europe 2023に参加するためのすべての無料バーチャルセッション」
• 「ODSC EuropeのML for Financeトラックで経済をより深く理解しましょう」
• 「ODSC Europe 2023のトップバーチャルセッションをこちらでご覧ください」

トランスフォーマーベースのエンコーダーデコーダーモデルは、表現学習とモデルアーキテクチャに関する数年にわたる研究の成果です。このノートブックでは、ニューラルエンコーダーデコーダーモデルの歴史の簡単な概要を提供します。詳細については、Sebastion Ruder氏の素晴らしいブログ記事を読むことをお勧めします。また、セルフアテンションアーキテクチャの基本的な理解も推奨されます。以下のJay Alammar氏のブログ記事は、元のトランスフォーマーモデルの復習として役立ちます。

このノートブックの執筆時点では、🤗Transformersには、T5、Bart、MarianMT、Pegasusのエンコーダーデコーダーモデルが含まれており、これらはモデルの要約についてはドキュメントで要約されています。

このノートブックは4つのパートに分かれています：

• 背景 – ニューラルエンコーダーデコーダーモデルの短い歴史がRNNベースのモデルに焦点を当てて与えられます。
• エンコーダーデコーダー – トランスフォーマーベースのエンコーダーデコーダーモデルが紹介され、そのモデルが推論に使用される方法が説明されます。
• エンコーダー – モデルのエンコーダーパートが詳細に説明されます。
• デコーダー – モデルのデコーダーパートが詳細に説明されます。

各パートは前のパートを基に構築されていますが、単体でも読むことができます。

背景

自然言語生成（NLG）のタスクは、NLPのサブフィールドであるシーケンス対シーケンスの問題として最も適しています。このようなタスクは、入力単語のシーケンスをターゲット単語のシーケンスにマッピングするモデルを見つけることと定義できます。いくつかの代表的な例としては、要約や翻訳があります。以下では、各単語がベクトル表現にエンコードされると仮定します。そのため、n個の入力単語はn個の入力ベクトルのシーケンスとして表現することができます：

X 1 : n = { x 1 , … , x n } . \mathbf{X}_{1:n} = \{\mathbf{x}_1, \ldots, \mathbf{x}_n\}. X 1 : n ​ = { x 1 ​ , … , x n ​ } .

したがって、シーケンス対シーケンスの問題は、入力ベクトルのシーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​ から目標ベクトルのシーケンス Y 1 : m \mathbf{Y}_{1:m} Y 1 : m ​ へのマッピング f f f を見つけることによって解決することができます。ただし、目標ベクトルの数 m m m は事前には不明であり、入力シーケンスに依存します：

f : X 1 : n → Y 1 : m . f: \mathbf{X}_{1:n} \to \mathbf{Y}_{1:m}. f

X 1 : n ​ → Y 1 : m ​ .

Sutskever et al.（2014）は、ディープニューラルネットワーク（DNN）は「柔軟性とパワーにもかかわらず、入力とターゲットを固定次元のベクトルで適切にエンコードできるマッピングのみを定義することができる」と述べています。 1 {}^1 1

シーケンス・トゥ・シーケンスの問題を解決するために、DNNモデル2 {}^2 2 を使用すると、ターゲットベクトルの数 m m m が事前に知られていなければならず、入力 X 1 : n \mathbf{X}_{1:n} X 1 : n ​ に依存しない必要があります。これはサブオプティマルです。なぜなら、NLGのタスクでは、ターゲットワードの数は通常、入力 X 1 : n \mathbf{X}_{1:n} X 1 : n ​ だけでなく、入力の長さ n n n に依存するからです。例えば、1000語の記事は、内容に応じて200語または100語の要約になることがあります。

2014年、ChoらとSutskeverらは、シーケンス・トゥ・シーケンスのタスクにおいて、再帰ニューラルネットワーク（RNN）だけを使用したエンコーダ・デコーダモデルの提案を行いました。DNNとは異なり、RNNは可変数のターゲットベクトルのマッピングをモデリングすることができます。RNNベースのエンコーダ・デコーダモデルの動作について詳しく見てみましょう。

推論中、エンコーダRNNは入力シーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​ をエンコードし、隠れ状態を更新することによりエンコードします 3 {}^3 3 。最後の入力ベクトル x n \mathbf{x}_n x n ​ を処理した後、エンコーダの隠れ状態は入力エンコーディング c \mathbf{c} c を定義します。したがって、エンコーダは次のマッピングを定義します：

f θ e n c : X 1 : n → c . f_{\theta_{enc}}: \mathbf{X}_{1:n} \to \mathbf{c}. f θ e n c ​ ​ : X 1 : n ​ → c .

次に、デコーダの隠れ状態は入力エンコーディングで初期化され、推論中にデコーダRNNが使用されて目標シーケンスを自己回帰的に生成します。説明しましょう。

数学的には、デコーダは隠れ状態 c \mathbf{c} c が与えられたときの目標シーケンス Y 1 : m \mathbf{Y}_{1:m} Y 1 : m ​ の確率分布を定義します：

p θ d e c ( Y 1 : m ∣ c ) . p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c}). p θ d e c ​ ​ ( Y 1 : m ​ ∣ c ) .

ベイズの定理により、確率分布は次のように単一のターゲットベクトルの条件付き分布に分解できます：

p θ d e c ( Y 1 : m ∣ c ) = ∏ i = 1 m p θ dec ( y i ∣ Y 0 : i − 1 , c ) . p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c}) = \prod_{i=1}^{m} p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}). p θ d e c ​ ​ ( Y 1 : m ​ ∣ c ) = i = 1 ∏ m ​ p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , c ) .

したがって、アーキテクチャが次のターゲットベクトルの条件付き分布をモデリングできる場合：

p θ dec ( y i ∣ Y 0 : i − 1 , c ) , ∀ i ∈ { 1 , … , m } , p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}), \forall i \in \{1, \ldots, m\}, p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , c ) , ∀ i ∈ { 1 , … , m } ,

そのため、単純にすべての条件付き確率を掛け合わせることで、隠れ状態 c \mathbf{c} c に対する任意の目標ベクトルシーケンスの分布をモデリングすることができます。

では、RNNベースのデコーダアーキテクチャは p θ dec ( y i ∣ Y 0

: i − 1 , c ) p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}) p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , c ) をどのようにモデリングするのでしょうか？

計算的な観点では、モデルは前の内部隠れ状態 c i − 1 \mathbf{c}_{i-1} c i − 1 ​ と前の目標ベクトル y i − 1 \mathbf{y}_{i-1} y i − 1 ​ を現在の内部隠れ状態 c i \mathbf{c}_i c i ​ とロジットベクトル l i \mathbf{l}_i l i ​ に順次マッピングします（以下の赤色の部分に表示されています）：

f θ dec ( y i − 1 , c i − 1 ) → l i , c i . f_{\theta_{\text{dec}}}(\mathbf{y}_{i-1}, \mathbf{c}_{i-1}) \rightarrow \mathbf{l}_i, \mathbf{c}_i. f θ dec ​ ​ ( y i − 1 ​ , c i − 1 ​ ) → l i ​ , c i ​ . c 0 \mathbf{c}_0 c 0 ​ は、RNNベースのエンコーダの出力隠れ状態として定義されます。その後、ソフトマックス演算を使用して、ロジットベクトル l i \mathbf{l}_i l i ​ を次の目標ベクトルの条件付き確率分布に変換します：

p ( y i ∣ l i ) = Softmax ( l i ) , with l i = f θ dec ( y i − 1 , c prev ) . p(\mathbf{y}_i | \mathbf{l}_i) = \textbf{Softmax}(\mathbf{l}_i), \text{ with } \mathbf{l}_i = f_{\theta_{\text{dec}}}(\mathbf{y}_{i-1}, \mathbf{c}_{\text{prev}}). p ( y i ​ ∣ l i ​ ) = Softmax ( l i ​ ) , with l i ​ = f θ dec ​ ​ ( y i − 1 ​ , c prev ​ ) .

ロジットベクトルとその結果の確率分布の詳細については、注釈4をご覧ください {}^4 4 。上記の式からわかるように、現在の目標ベクトル y i \mathbf{y}_i y i ​ の分布は、直接前の目標ベクトル y i − 1 \mathbf{y}_{i-1} y i − 1 ​ と前の隠れ状態 c i − 1 \mathbf{c}_{i-1} c i − 1 ​ に依存しています。前の隠れ状態 c i − 1 \mathbf{c}_{i-1} c i − 1 ​ は、すべての前の目標ベクトル y 0 , … , y i − 2 \mathbf{y}_0, \ldots, \mathbf{y}_{i-2} y 0 ​ , … , y i − 2 ​ に依存するため、RNNベースのデコーダは条件付き分布 p θ dec ( y i ∣ Y 0 : i − 1 , c ) p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}) p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , c ) を暗黙的に（例えば、間接的に）モデル化しています。

可能な目標ベクトルの系列 Y 1 : m \mathbf{Y}_{1:m} Y 1 : m ​ の空間は非常に大きいため、推論時には効率的に高確率の目標ベクトルの系列をサンプリングするためのデコーディング手法 5 {}^5 5 に頼る必要があります。これは条件付き確率分布 p θ d e c ( Y 1 : m ∣ c ) p_{\theta_{dec}}(\mathbf{Y}_{1:m} |\mathbf{c}) p θ d e c ​ ​ ( Y 1 : m ​ ∣ c ) から高確率の目標ベクトルの系列を効率的にサンプリングします。

このようなデコーディング手法が与えられた場合、推論中に次の入力ベクトル y i \mathbf{y}_i y i ​ は p θ dec ( y i ∣ Y 0 : i − 1 , c ) p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}) p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , c ) からサンプリングされ、その後、デコーダRNNは p θ dec ( y i + 1 ∣ Y 0 : i , c ) p_{\theta_{\text{dec}}}(\mathbf{y}_{i+1} | \mathbf{Y}_{0: i}, \mathbf{c}) p θ dec ​ ​ ( y i + 1 ​ ∣ Y 0 : i ​ , c ) をモデル化して、次の入力ベクトル y i + 1 \mathbf{y}_{i+1} y i + 1 ​ などを自己回帰的にサンプリングします。

RNNベースのエンコーダーデコーダーモデルの重要な特徴は、EOS（終了シーケンス）ベクトルとBOS（開始シーケンス）ベクトルなどの特別なベクトルの定義です。EOSベクトルは、入力シーケンスが終了したことをエンコーダーに伝え、またターゲットシーケンスの終了を定義するために使用されます。EOSがロジットベクトルからサンプリングされると、生成は完了します。BOSベクトルは、デコーダーRNNに最初のデコードステップで供給される入力ベクトルy0を表します。最初のログットl1を出力するためには、入力が必要ですが、最初のステップではまだ入力が生成されていないため、特別なBOSベクトルがデコーダーRNNに供給されます。わかりました – かなり複雑ですね！例を示して、説明していきましょう。

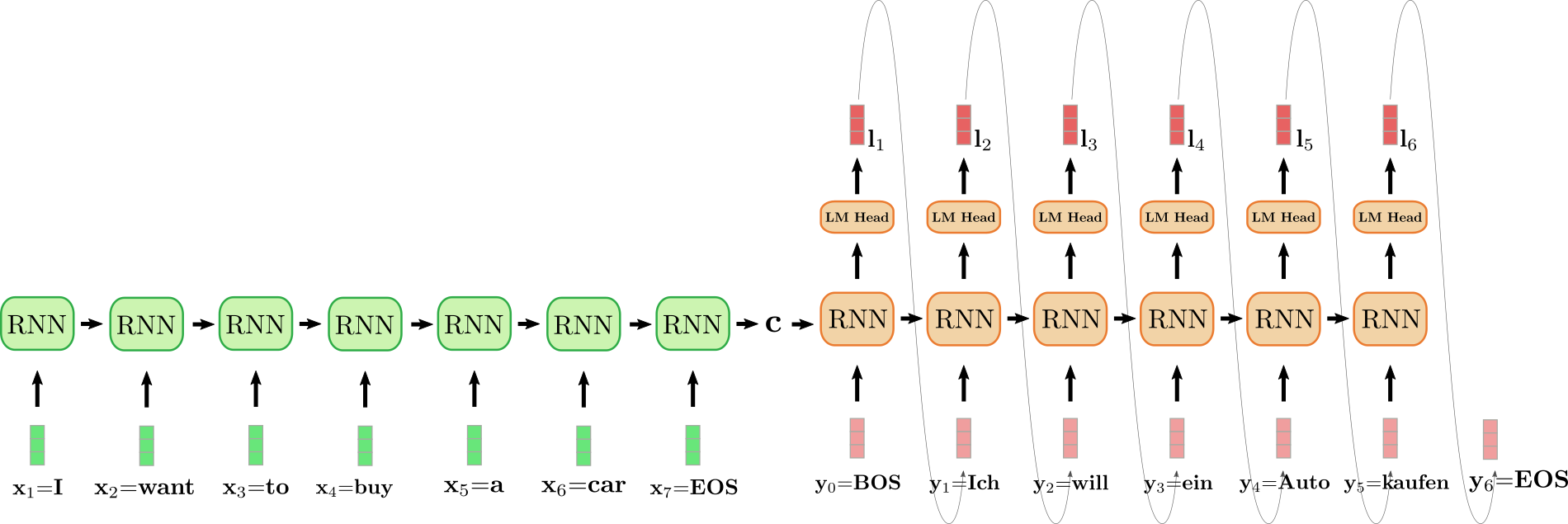
展開されたRNNエンコーダーは緑色で、展開されたRNNデコーダーは赤色です。

英語の文「I want to buy a car」は、x1 = I、x2 = want、x3 = to、x4 = buy、x5 = a、x6 = car、およびx7 = EOSとして表され、ドイツ語に翻訳されます。「Ich will ein Auto kaufen」として定義され、y0 = BOS、y1 = Ich、y2 = will、y3 = ein、y4 = Auto、y5 = kaufen、およびy6 = EOSです。まず、入力ベクトルx1 = IはエンコーダーRNNによって処理され、その隠れ状態が更新されます。エンコーダーRNNのターゲットベクトルは興味がないため、最終的なエンコーダーの隠れ状態cを無視することができます。エンコーダーRNNは、want、to、buy、a、car、EOSという入力文の残りの部分を同様の方法で処理し、各ステップで隠れ状態を更新します。ベクトルx7 = EOSに到達するまで、エンコーダーRNNの展開された水平矢印は隠れ状態の順次更新を表しています。エンコーダーRNNの最終的な隠れ状態cは、入力シーケンスのエンコーディングを完全に定義し、デコーダーRNNの初期隠れ状態として使用されます。これは、デコーダーRNNをエンコードされた入力に条件付けると考えることができます。

最初のターゲットベクトルを生成するために、デコーダーはBOSベクトル（上記のy0）を受け取ります。RNNのターゲットベクトルは、LMヘッドの順送信層を介してログットベクトルl1にさらにマッピングされ、最初のターゲットベクトルの条件付き分布を定義します。

p θ d e c ( y ∣ BOS , c ) .

p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{c}).

p θ d e c ​ ​ ( y ∣ BOS , c ) .

The word Ich is sampled (shown by the grey arrow, connecting l 1 and y 1 ) and consequently the second target vector can be sampled:

will ∼ p θ d e c ( y ∣ BOS , Ich , c ) .

will \sim p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \text{Ich}, \mathbf{c}).

will ∼ p θ d e c ​ ​ ( y ∣ BOS , Ich , c ) .

And so on until at step i = 6 , the EOS vector is sampled from l 6 and the decoding is finished. The resulting target sequence amounts to Y 1 : 6 = { y 1 , … , y 6 } , which is “Ich will ein Auto kaufen” in our example above.

To sum it up, an RNN-based encoder-decoder model, represented by f θ enc and p θ dec defines the distribution p ( Y 1 : m ∣ X 1 : n ) by factorization:

p_{\theta_{enc}, \theta_{dec}}(\mathbf{Y}_{1:m} | \mathbf{X}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{enc}, \theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{X}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{c}), \text{ with } \mathbf{c}=f_{\theta_{enc}}(X).

During inference, efficient decoding methods can auto-regressively generate the target sequence Y 1 : m .

The RNN-based encoder-decoder model took the NLG community by storm. In 2016, Google announced to fully replace its heavily feature engineered translation service by a single RNN-based encoder-decoder model (see here ).

Nevertheless, RNN-based encoder-decoder models have two pitfalls. First, RNNs suffer from the vanishing gradient problem, making it very difficult to capture long-range dependencies, cf. Hochreiter et al. (2001) . Second, the inherent recurrent architecture of RNNs prevents efficient parallelization when encoding, cf. Vaswani et al. (2017) .

---

1 {}^1 1 論文からの元の引用は、「 DNNは柔軟性とパワーを持っていますが、入力とターゲットが固定次元のベクトルで適切にエンコードできる問題にのみ適用できます 」というもので、ここでは少し適応されています。

2 {}^2 2 畳み込みニューラルネットワーク（CNN）についても基本的に同じことが言えます。可変長の入力シーケンスをCNNに入力することはできますが、ターゲットの次元は常に入力の次元に依存するか、特定の値に固定されます。

3 {}^3 3 最初のステップでは、隠れ状態はゼロベクトルとして初期化され、最初の入力ベクトルx 1 \mathbf{x}_1 x 1 ​ とともにRNNに供給されます。

4 {}^4 4 ニューラルネットワークは、すべての単語に対する確率分布を定義できます。すなわち、以下のようにp ( y ∣ c , Y 0 : i − 1 ) p(\mathbf{y} | \mathbf{c}, \mathbf{Y}_{0: i-1}) p ( y ∣ c , Y 0 : i − 1 ​ ) です。まず、ネットワークは入力c , Y 0 : i − 1 \mathbf{c}, \mathbf{Y}_{0: i-1} c , Y 0 : i − 1 ​ から埋め込みベクトル表現y ′ \mathbf{y’} y ′ へのマッピングを定義します。埋め込みベクトル表現y ′ \mathbf{y’} y ′ は次に「言語モデルヘッド」レイヤーに渡され、つまり単語埋め込み行列であるY vocab \mathbf{Y}^{\text{vocab}} Y vocab と乗算され、y ′ \mathbf{y’} y ′ とエンコードされたベクトルy ∈ Y vocab \mathbf{y} \in \mathbf{Y}^{\text{vocab}} y ∈ Y vocab の間のスコアが計算されます。結果のベクトルは、ロジットベクトルl = Y vocab y ′ \mathbf{l} = \mathbf{Y}^{\text{vocab}} \mathbf{y’} l = Y vocab y ′ と呼ばれ、ソフトマックス操作を適用することですべての単語に対する確率分布にマッピングできます：p ( y ∣ c ) = Softmax ( Y vocab y ′ ) = Softmax ( l ) p(\mathbf{y} | \mathbf{c}) = \text{Softmax}(\mathbf{Y}^{\text{vocab}} \mathbf{y’}) = \text{Softmax}(\mathbf{l}) p ( y ∣ c ) = Softmax ( Y vocab y ′ ) = Softmax ( l ) 。

5 {}^5 5 ビームサーチデコーディングはそのようなデコーディング方法の一例です。このノートブックでは、異なるデコーディング方法は対象外です。読者はデコーディング方法については、この対話型ノートブックを参照することをお勧めします。

6 {}^6 6 Sutskeverら（2014）は、上記の例では入力ベクトルがx 1 = car \mathbf{x}_1 = \text{car} x 1 ​ = car、x 2 = a \mathbf{x}_2 = \text{a} x 2 ​ = a、x 3 = buy \mathbf{x}_3 = \text{buy} x 3 ​ = buy、x 4 = to \mathbf{x}_4 = \text{to} x 4 ​ = to、x 5 = want \mathbf{x}_5 = \text{want} x 5 ​ = want、x 6 = I \mathbf{x}_6 = \text{I} x 6 ​ = I、およびx 7 = EOS \mathbf{x}_7 = \text{EOS} x 7 ​ = EOS に対応するように入力の順序を逆にしています。これは、x 6 = I \mathbf{x}_6 = \text{I} x 6 ​ = I とy 1 = Ich \mathbf{y}_1 = \text{Ich} y 1 ​ = Ich のような対応する単語ペア間の短い接続を可能にするためです。研究グループは、入力シーケンスの逆転が彼らのモデルの機械翻訳での性能向上の主な理由であったことを強調しています。

エンコーダーデコーダー

2017年、Vaswaniらはトランスフォーマーを紹介し、トランスフォーマーベースのエンコーダーデコーダーモデルが生まれました。

エンコーダとデコーダの両方が残差注意ブロックのスタックで構成される、RNNベースのエンコーダ-デコーダモデルに類似したトランスフォーマベースのエンコーダ-デコーダモデル。トランスフォーマベースのエンコーダ-デコーダモデルの主なイノベーションは、このような残差注意ブロックが再帰的な構造を示さずに、可変長の入力シーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​ を処理できることです。再帰的な構造に依存しないことにより、トランスフォーマベースのエンコーダ-デコーダは高度に並列化可能であり、モダンなハードウェア上のRNNベースのエンコーダ-デコーダモデルと比べて計算効率が桁違いに向上しています。

再確認ですが、シーケンス対シーケンスの問題を解決するためには、可変長の入力シーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​ を可変長の出力シーケンス Y 1 : m \mathbf{Y}_{1:m} Y 1 : m ​ にマッピングする方法を見つける必要があります。トランスフォーマベースのエンコーダ-デコーダモデルがこのようなマッピングを見つけるためにどのように使用されるかを見てみましょう。

RNNベースのエンコーダ-デコーダモデルと同様に、トランスフォーマベースのエンコーダ-デコーダモデルは、入力シーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​ に対するターゲットベクトル Y 1 : n \mathbf{Y}_{1:n} Y 1 : n ​ の条件付き分布を定義します：

p θ enc , θ dec ( Y 1 : m ∣ X 1 : n ) . p_{\theta_{\text{enc}}, \theta_{\text{dec}}}(\mathbf{Y}_{1:m} | \mathbf{X}_{1:n}). p θ enc ​ , θ dec ​ ​ ( Y 1 : m ​ ∣ X 1 : n ​ ) .

トランスフォーマベースのエンコーダ部は、入力シーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​ を隠れた状態のシーケンス X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ にエンコードし、次のマッピングを定義します：

f θ enc : X 1 : n → X ‾ 1 : n . f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n}. f θ enc ​ ​ : X 1 : n ​ → X 1 : n ​ .

トランスフォーマベースのデコーダ部は、エンコードされた隠れた状態のシーケンス X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ と過去のターゲットベクトルシーケンス Y 0 : i − 1 \mathbf{Y}_{0:i-1} Y 0 : i − 1 ​ が与えられた場合のターゲットベクトルシーケンス Y 1 : n \mathbf{Y}_{1:n} Y 1 : n ​ の条件付き確率分布をモデル化します：

p θ d e c ( Y 1 : n ∣ X ‾ 1 : n ) . p_{\theta_{dec}}(\mathbf{Y}_{1:n} | \mathbf{\overline{X}}_{1:n}). p θ d e c ​ ​ ( Y 1 : n ​ ∣ X 1 : n ​ ) .

ベイズの定理により、この分布はエンコードされた隠れた状態 X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ とすべての前のターゲットベクトル Y 0 : i − 1 \mathbf{Y}_{0:i-1} Y 0 : i − 1 ​ が与えられた場合のターゲットベクトル y i \mathbf{y}_i y i ​ の条件付き確率分布の積に因数分解できます：

p θ d e c ( Y 1 : n ∣ X ‾ 1 : n ) = ∏ i = 1 n p θ dec ( y i ∣ Y 0 : i − 1 , X ‾ 1 : n ) . p_{\theta_{dec}}(\mathbf{Y}_{1:n} | \mathbf{\overline{X}}_{1:n}) = \prod_{i=1}^{n} p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}). p θ d e c ​ ​ ( Y 1 : n ​ ∣ X 1 : n ​ ) = i = 1 ∏ n ​ p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , X 1 : n ​ ) .

トランスフォーマーベースのデコーダーは、符号化された隠れ状態のシーケンス X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ と以前のターゲットベクトル Y 0 : i − 1 \mathbf{Y}_{0:i-1} Y 0 : i − 1 ​ を、対数確率ベクトル l i \mathbf{l}_i l i ​ にマッピングします。次に、対数確率ベクトル l i \mathbf{l}_i l i ​ はソフトマックス演算によって処理され、条件付き分布 p θ dec ( y i ∣ Y 0 : i − 1 , X ‾ 1 : n ) p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}) p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , X 1 : n ​ ) を定義します。これは、RNNベースのデコーダーと同様に行われます。ただし、RNNベースのデコーダーとは異なり、目標ベクトル y i \mathbf{y}_i y i ​ の分布は明示的に（または直接的に）すべての以前の目標ベクトル y 0 , … , y i − 1 \mathbf{y}_0, \ldots, \mathbf{y}_{i-1} y 0 ​ , … , y i − 1 ​ に依存するように条件付けられます。後ほど詳細に説明しますが、ここで 0 番目の目標ベクトル y 0 \mathbf{y}_0 y 0 ​ は、特別な「文の始まり」BOS \text{BOS} BOS ベクトルで表されます。

条件付き分布 p θ dec ( y i ∣ Y 0 : i − 1 , X ‾ 1 : n ) p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}) p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , X 1 : n ​ ) を定義したので、出力の自己回帰的生成を行い、推論時に入力シーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​ から出力シーケンス Y 1 : m \mathbf{Y}_{1:m} Y 1 : m ​ を定義することができます。

トランスフォーマーベースのエンコーダーは緑色で表示され、トランスフォーマーベースのデコーダーは赤色で表示されます。前のセクションと同様に、英語の文「I want to buy a car」が x 1 = I \mathbf{x}_1 = \text{I} x 1 ​ = I, x 2 = want \mathbf{x}_2 = \text{want} x 2 ​ = want, x 3 = to \mathbf{x}_3 = \text{to} x 3 ​ = to, x 4 = buy \mathbf{x}_4 = \text{buy} x 4 ​ = buy, x 5 = a \mathbf{x}_5 = \text{a} x 5 ​ = a, x 6 = car \mathbf{x}_6 = \text{car} x 6 ​ = car, および x 7 = EOS \mathbf{x}_7 = \text{EOS} x 7 ​ = EOS で表され、これがドイツ語に翻訳される例として y 0 = BOS \mathbf{y}_0 = \text{BOS} y 0 ​ = BOS, y 1 = Ich \mathbf{y}_1 = \text{Ich} y 1 ​ = Ich, y 2 = will \mathbf{y}_2 = \text{will} y 2 ​ = will, y 3 = ein \mathbf{y}_3 = \text{ein} y 3 ​ = ein, y 4 = Auto , y 5 = kaufen \mathbf{y}_4 = \text{Auto}, \mathbf{y}_5 = \text{kaufen} y 4 ​ = Auto, y 5 ​ = kaufen, および y 6 = EOS \mathbf{y}_6=\text{EOS} y 6 ​ = EOS と定義されます。

まず、エンコーダーは完全な入力シーケンス X 1 : 7 \mathbf{X}_{1:7} X 1 : 7 ​ = “私は車を買いたいです”（薄い緑のベクトルで表される）を、文脈を持ったエンコードされたシーケンス X ‾ 1 : 7 \mathbf{\overline{X}}_{1:7} X 1 : 7 ​ に処理します。例えば、x ‾ 4 \mathbf{\overline{x}}_4 x 4 ​ は、”買う”という入力 x 4 \mathbf{x}_4 x 4 ​ だけでなく、他のすべての単語 “私”, “したい”, “車”, “を”、”EOS”に依存するエンコーディングを定義します。

次に、入力エンコード X ‾ 1 : 7 \mathbf{\overline{X}}_{1:7} X 1 : 7 ​ とBOSベクトル、つまり y 0 \mathbf{y}_0 y 0 ​ をデコーダーに送ります。デコーダーは入力 X ‾ 1 : 7 \mathbf{\overline{X}}_{1:7} X 1 : 7 ​ と y 0 \mathbf{y}_0 y 0 ​ を処理し、最初のロジット l 1 \mathbf{l}_1 l 1 ​（濃い赤で表示される）を定義して、最初のターゲットベクトル y 1 \mathbf{y}_1 y 1 ​ の条件付き分布を定義します：

p θ e n c , d e c ( y ∣ y 0 , X 1 : 7 ) = p θ e n c , d e c ( y ∣ BOS , 私 は 車 を 買いたい です EOS ) = p θ d e c ( y ∣ BOS , X ‾ 1 : 7 ) . p_{\theta_{enc, dec}}(\mathbf{y} | \mathbf{y}_0, \mathbf{X}_{1:7}) = p_{\theta_{enc, dec}}(\mathbf{y} | \text{BOS}, \text{私 は 車 を 買いたい です EOS}) = p_{\theta_{dec}}(\mathbf{y} | \text{BOS}, \mathbf{\overline{X}}_{1:7}). p θ e n c , d e c ​ ​ ( y ∣ y 0 ​ , X 1 : 7 ​ ) = p θ e n c , d e c ​ ​ ( y ∣ BOS , 私 は 車 を 買いたい です EOS ) = p θ d e c ​ ​ ( y ∣ BOS , X 1 : 7 ​ ) .

次に、第一のターゲットベクトル y 1 \mathbf{y}_1 y 1 ​ = “私” が分布からサンプリングされます（灰色の矢印で表されます）そしてデコーダーに再びフィードされます。デコーダーは今度は y 0 \mathbf{y}_0 y 0 ​ = “BOS” と y 1 \mathbf{y}_1 y 1 ​ = “私” の両方を処理し、2番目のターゲットベクトル y 2 \mathbf{y}_2 y 2 ​ の条件付き分布を定義します：

p θ d e c ( y ∣ BOS 私 , X ‾ 1 : 7 ) . p_{\theta_{dec}}(\mathbf{y} | \text{BOS 私}, \mathbf{\overline{X}}_{1:7}). p θ d e c ​ ​ ( y ∣ BOS 私 , X 1 : 7 ​ ) .

再びサンプリングし、ターゲットベクトル y 2 \mathbf{y}_2 y 2 ​ = “will” を生成します。私たちは自己回帰的な方法で続け、6ステップ目でEOSベクトルが条件付き分布からサンプリングされます：

EOS ∼ p θ d e c ( y ∣ BOS 私 will ein Auto kaufen , X ‾ 1 : 7 ) . \text{EOS} \sim p_{\theta_{dec}}(\mathbf{y} | \text{BOS 私 will ein Auto kaufen}, \mathbf{\overline{X}}_{1:7}). EOS ∼ p θ d e c ​ ​ ( y ∣ BOS 私 will ein Auto kaufen , X 1 : 7 ​ ) .

そして、自己回帰的な方法で続きます。

エンコーダーは、最初の順方向パスでのみ使用され、X 1 : n \mathbf{X}_{1:n} X 1 : n ​ を X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ にマッピングします。2回目の順方向パス以降、デコーダーは以前に計算されたエンコーディング X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ を直接使用することができます。わかりやすくするために、上記の例の最初の順方向パスと2番目の順方向パスを図で示します。

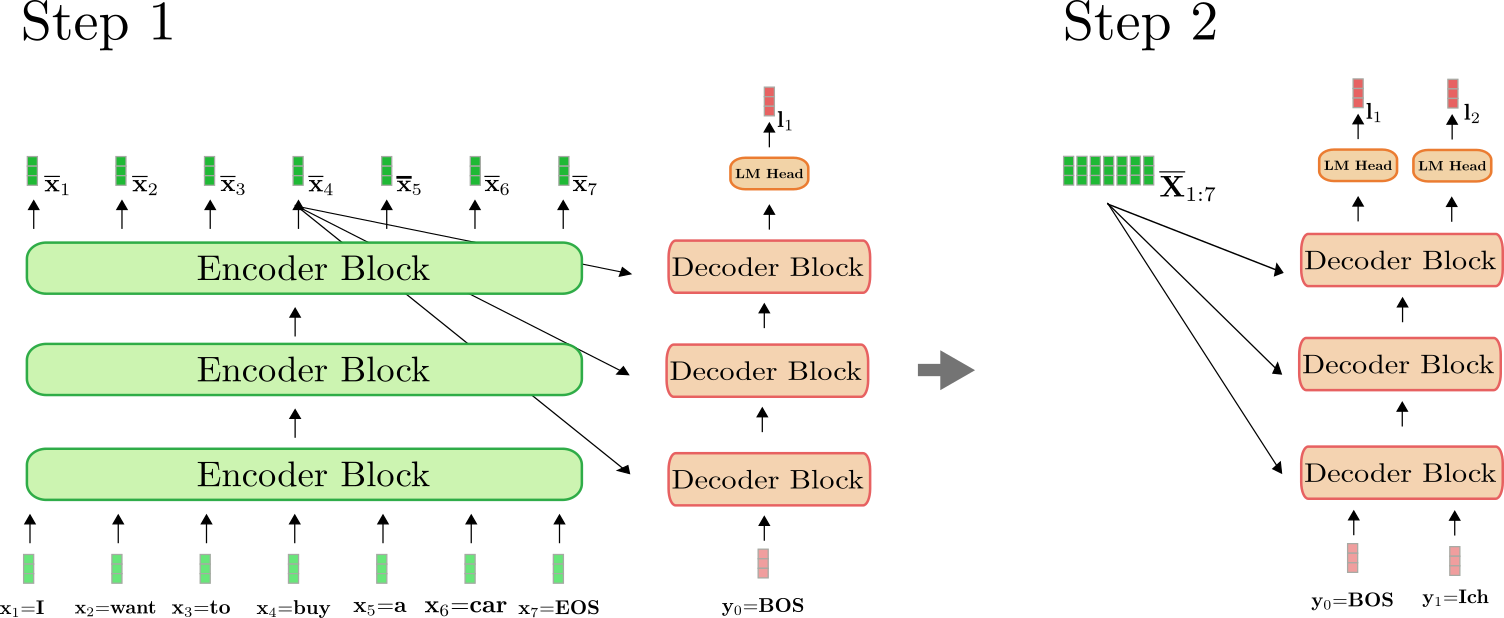
上記の図から分かるように、ステップ i = 1 i=1 i = 1 のみ、「私は車を買いたいEOS」という文を X ‾ 1 : 7 \mathbf{\overline{X}}_{1:7} X 1 : 7 ​ にエンコードする必要があります。ステップ i = 2 i=2 i = 2 では、「私は車を買いたいEOS」の文の文脈化されたエンコーディングはデコーダーによって再利用されます。

🤗Transformersでは、この自己回帰的な生成は、.generate()メソッドを呼び出すことで裏で行われます。翻訳モデルの一つを使用して、これがどのように動作するかを見てみましょう。

from transformers import MarianMTModel, MarianTokenizer

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

# エンコードされた入力ベクトルのIDを作成
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# 例を翻訳
output_ids = model.generate(input_ids)[0]

# デコードして表示
print(tokenizer.decode(output_ids))

出力:

    <pad> Ich will ein Auto kaufen

.generate()を呼び出すと、裏で多くの処理が行われます。まず、input_idsをエンコーダーに渡します。次に、エンコードされたinput_idsとMarianMTModelの場合は <pad> \text{<pad>} <pad> シンボルと共に事前定義されたトークンをデコーダーに渡します。そして、ビームサーチデコーディングメカニズムを適用して、直前のデコーダーの出力1 {}^1 1の次の出力単語を自己回帰的にサンプリングします。ビームサーチデコーディングの詳細については、このブログ記事を参照してください。

付録では、シンプルな生成メソッドが「ゼロから」実装されるコードの断片を示しています。自己回帰的な生成が裏でどのように動作するかを完全に理解するためには、付録を読むことを強くお勧めします。

まとめると：

• トランスフォーマベースのエンコーダーは、入力シーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​ を文脈化されたエンコーディングシーケンス X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ にマッピングします。
• トランスフォーマベースのデコーダーは、条件付き分布 p θ dec ( y i ∣ Y 0 : i − 1 , X ‾ 1 : n ) p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}) p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , X 1 : n ​ ) を定義します。
• 適切なデコーディングメカニズムが与えられれば、出力シーケンス Y 1 : m \mathbf{Y}_{1:m} Y 1 : m ​ は、p θ dec ( y i ∣ Y 0 : i − 1 , X ‾ 1 : n ) , ∀ i ∈ { 1 , … , m } p_{\theta_{\text{dec}}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}), \forall i \in \{1, \ldots, m\} p θ dec ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , X 1 : n ​ ) , ∀ i ∈ { 1 , … , m } から自己回帰的にサンプリングされます。

素晴らしいですね、トランスフォーマーベースのエンコーダデコーダモデルの概要を把握したので、モデルのエンコーダとデコーダの部分についても詳しく見ていきましょう。具体的には、エンコーダがセルフアテンション層を使って文脈依存のベクトルエンコーディングのシーケンスを生成する方法と、セルフアテンション層によって効率的な並列処理が可能になる方法を詳しく見ていきます。その後、デコーダモデルのセルフアテンション層がどのように機能し、エンコーダの出力に対してクロスアテンション層を使ってデコーダが条件付けられる方法を詳しく説明します。また、トランスフォーマーベースのエンコーダデコーダモデルが、RNNベースのエンコーダデコーダモデルの長距離依存性の問題を解決する方法が明らかになるでしょう。

---

1 {}^1 1 "Helsinki-NLP/opus-mt-en-de" の場合、デコードパラメータはこちらでアクセスできます。モデルは num_beams=6 を使ってビームサーチを適用していることがわかります。

エンコーダ

前のセクションで述べたように、トランスフォーマーベースのエンコーダは入力シーケンスを文脈に応じたエンコーディングシーケンスにマッピングします：

f θ enc : X 1 : n → X ‾ 1 : n . f_{\theta_{\text{enc}}}: \mathbf{X}_{1:n} \to \mathbf{\overline{X}}_{1:n}. f θ enc ​ ​ : X 1 : n ​ → X 1 : n ​ .

アーキテクチャを詳しく見てみると、トランスフォーマーベースのエンコーダは、リジュアルエンコーダブロックのスタックです。各エンコーダブロックは、双方向のセルフアテンション層と、その後に2つの順伝播層から成り立っています。このノートブックでは簡単のため、正規化層は無視します。また、2つの順伝播層の役割については詳しく議論しませんが、エンコーダブロックごとに必要な最終的なベクトルからベクトルへのマッピングとして見ることにします。双方向のセルフアテンション層は、各入力ベクトル x ′ j , ∀ j ∈ { 1 , … , n } \mathbf{x’}_j, \forall j \in \{1, \ldots, n\} x ′ j ​ , ∀ j ∈ { 1 , … , n } をすべての入力ベクトル x ′ 1 , … , x ′ n \mathbf{x’}_1, \ldots, \mathbf{x’}_n x ′ 1 ​ , … , x ′ n ​ と関連付け、入力ベクトル x ′ j \mathbf{x’}_j x ′ j ​ をより「洗練された」文脈に依存した表現 x ′ ′ j \mathbf{x”}_j x ′ ′ j ​ に変換します。そのため、最初のエンコーダブロックは、入力シーケンス X 1 : n \mathbf{X}_{1:n} X 1 : n ​（以下のライトグリーンで示されています）の各入力ベクトルを文脈に依存したベクトル表現に変換し、続くエンコーダブロックではこの文脈表現をさらに洗練し、最後のエンコーダブロックで最終的な文脈エンコーディング X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​（以下のダーカーグリーンで示されています）を出力します。

エンコーダが入力シーケンス「I want to buy a car EOS」を文脈化されたエンコーディングシーケンスにどのように処理するかを可視化してみましょう。RNNベースのエンコーダと同様に、トランスフォーマーベースのエンコーダも特別な「シーケンスの終わり」を示すための入力ベクトルを入力シーケンスに追加します 2 {}^2 2 。

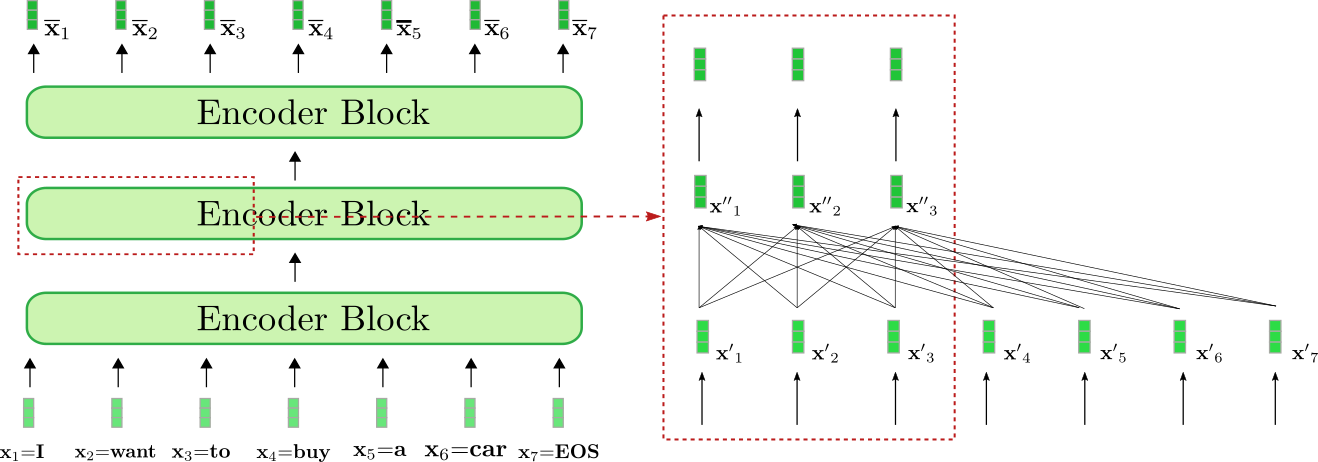
私たちの例題として、トランスフォーマーベースのエンコーダは3つのエンコーダブロックで構成されており、2つ目のエンコーダブロックは右側の赤いボックスで最初の3つの入力ベクトル x 1 , x 2 および x 3 \mathbf{x}_1, \mathbf{x}_2 および \mathbf{x}_3 x 1 ​ , x 2 ​ および x 3 ​ の詳細が示されています。双方向のセルフアテンションメカニズムは、赤いボックスの下部にある完全に接続されたグラフで示され、2つの順伝播層は赤いボックスの上部に表示されています。前述のように、私たちは双方向のセルフアテンションメカニズムに焦点を当てます。

自己注意層の各出力ベクトル x ′ ′ i , ∀ i ∈ { 1 , … , 7 } \mathbf{x”}_i, \forall i \in \{1, \ldots, 7\} x ′ ′ i ​ , ∀ i ∈ { 1 , … , 7 } は、すべての入力ベクトル x ′ 1 , … , x ′ 7 \mathbf{x’}_1, \ldots, \mathbf{x’}_7 x ′ 1 ​ , … , x ′ 7 ​ に直接依存しています。例えば、単語「want」の入力ベクトル表現である x ′ 2 \mathbf{x’}_2 x ′ 2 ​ は、「buy」という単語の x ′ 4 \mathbf{x’}_4 x ′ 4 ​ とも、「I」という単語の x ′ 1 \mathbf{x’}_1 x ′ 1 ​ とも直接的な関係があります。したがって、「want」の出力ベクトル表現である x ′ ′ 2 \mathbf{x”}_2 x ′ ′ 2 ​ は、「want」という単語のより洗練された文脈表現を表しています。

双方向の自己注意の動作をより詳しく見てみましょう。エンコーダーブロックの入力シーケンス X ′ 1 : n \mathbf{X’}_{1:n} X ′ 1 : n ​ の各入力ベクトル x ′ i \mathbf{x’}_i x ′ i ​ は、三つの学習可能な重み行列 W q , W v , W k \mathbf{W}_q, \mathbf{W}_v, \mathbf{W}_k W q ​ , W v ​ , W k ​ を介して、キーベクトル k i \mathbf{k}_i k i ​ 、値ベクトル v i \mathbf{v}_i v i ​ 、クエリベクトル q i \mathbf{q}_i q i ​ (以下の図でオレンジ、ブルー、パープルで表示) に射影されます。

q i = W q x ′ i , \mathbf{q}_i = \mathbf{W}_q \mathbf{x’}_i, q i ​ = W q ​ x ′ i ​ , v i = W v x ′ i , \mathbf{v}_i = \mathbf{W}_v \mathbf{x’}_i, v i ​ = W v ​ x ′ i ​ , k i = W k x ′ i , \mathbf{k}_i = \mathbf{W}_k \mathbf{x’}_i, k i ​ = W k ​ x ′ i ​ , ∀ i ∈ { 1 , … n } . \forall i \in \{1, \ldots n \}. ∀ i ∈ { 1 , … n } .

ここで注意しておきたいのは、同じ重み行列が各入力ベクトル x i , ∀ i ∈ { i , … , n } \mathbf{x}_i, \forall i \in \{i, \ldots, n\} x i ​ , ∀ i ∈ { i , … , n } に適用されるということです。各入力ベクトル x i \mathbf{x}_i x i ​ をクエリ、キー、値ベクトルに射影した後、各クエリベクトル q j , ∀ j ∈ { 1 , … , n } \mathbf{q}_j, \forall j \in \{1, \ldots, n\} q j ​ , ∀ j ∈ { 1 , … , n } は、すべてのキーベクトル k 1 , … , k n \mathbf{k}_1, \ldots, \mathbf{k}_n k 1 ​ , … , k n ​ と比較されます。クエリベクトル q j \mathbf{q}_j q j ​ に対してキーベクトル k 1 , … k n \mathbf{k}_1, \ldots \mathbf{k}_n k 1 ​ , … k n ​ の中で最も類似しているものほど、対応する値ベクトル v j \mathbf{v}_j v j ​ は出力ベクトル x ′ ′ j \mathbf{x”}_j x ′ ′ j ​ にとってより重要です。具体的には、出力ベクトル x ′ ′ j \mathbf{x”}_j x ′ ′ j ​ は、すべての値ベクトル v 1 , … , v n \mathbf{v}_1, \ldots, \mathbf{v}_n v 1 ​ , … , v n ​ の加重和に入力ベクトル x ′ j \mathbf{x’}_j x ′ j ​ を加えたものです。ここで、重みはクエリベクトル q j \mathbf{q}_j q j ​ と対応するキーベクトル k 1 , … , k n \mathbf{k}_1, \ldots, \mathbf{k}_n k 1 ​ , … , k n ​ のコサイン類似度に比例しており、数学的には以下の式で表される Softmax ( K 1 : n ⊺ q j ) \textbf{Softmax}(\mathbf{K}_{1:n}^\intercal \mathbf{q}_j) Softmax ( K 1 : n ⊺ ​ q j ​ ) です。自己注意層の完全な説明については、このブログ記事やオリジナルの論文を参照してください。

わかりました、これはかなり複雑そうです。上記の例のクエリベクトルの一つに対して、双方向自己注意層を図解してみましょう。簡単のために、私たちの例のTransformerベースのデコーダは単一のアテンションヘッドconfig.num_heads = 1のみを使用し、正規化は適用されないと仮定されています。

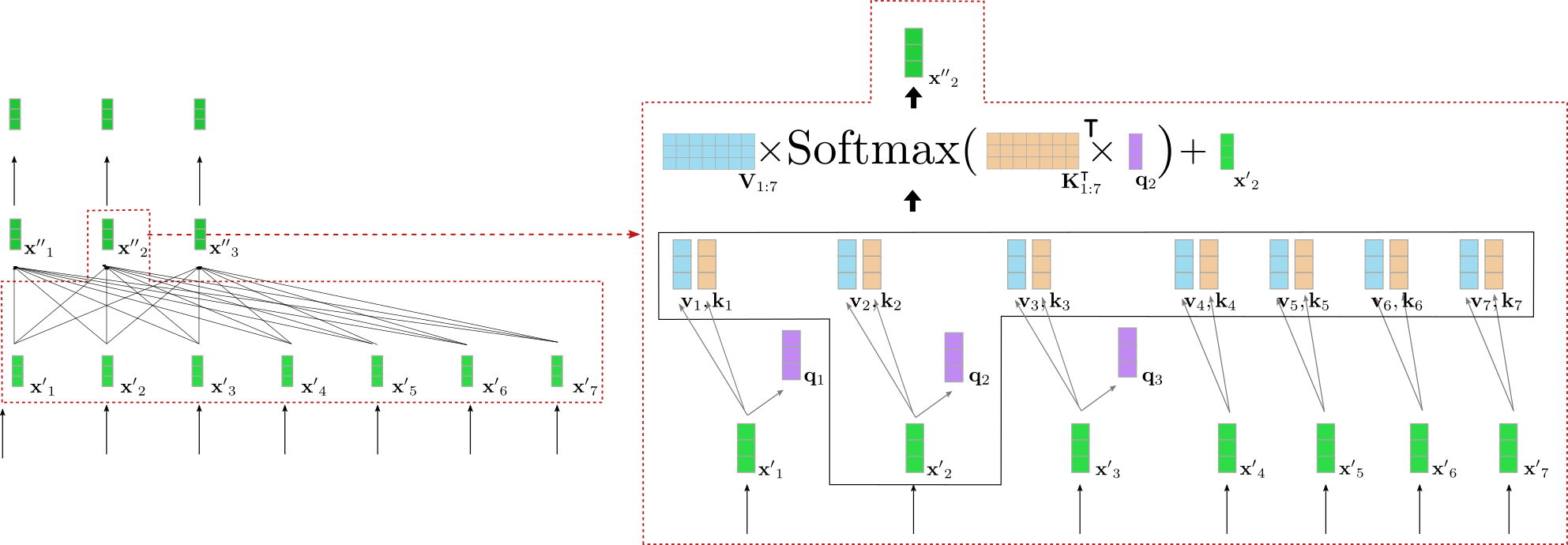
左側には、以前に示した2番目のエンコーダブロックが再表示され、右側には、入力単語「want」に対応する2番目の入力ベクトルx ′ 2 \mathbf{x’}_2 x ′ 2 ​の双方向自己注意メカニズムの詳細な可視化が示されています。最初に、すべての入力ベクトルx ′ 1 , … , x ′ 7 \mathbf{x’}_1, \ldots, \mathbf{x’}_7 x ′ 1 ​ , … , x ′ 7 ​は、それぞれのクエリベクトルq 1 , … , q 7 \mathbf{q}_1, \ldots, \mathbf{q}_7 q 1 ​ , … , q 7 ​（上記の紫色で示されているのは最初の3つのクエリベクトルのみです）に射影され、値ベクトルv 1 , … , v 7 \mathbf{v}_1, \ldots, \mathbf{v}_7 v 1 ​ , … , v 7 ​（青で示されています）、およびキーベクトルk 1 , … , k 7 \mathbf{k}_1, \ldots, \mathbf{k}_7 k 1 ​ , … , k 7 ​（オレンジで示されています）。次に、クエリベクトルq 2 \mathbf{q}_2 q 2 ​は、すべてのキーベクトルの転置、すなわち K 1 : 7 ⊺ \mathbf{K}_{1:7}^{\intercal} K 1 : 7 ⊺ ​との乗算を行い、softmax操作により自己注意ウェイトを生成します。最終的に、自己注意ウェイトは対応する値ベクトルと乗算され、入力ベクトルx ′ 2 \mathbf{x’}_2 x ′ 2 ​が追加されて、単語「want」の「洗練された」表現であるx ′ ′ 2 \mathbf{x”}_2 x ′ ′ 2 ​（右側の濃い緑で示されています）が出力されます。この全体の式は、右側のボックスの上部に示されています。K 1 : 7 ⊺ \mathbf{K}_{1:7}^{\intercal} K 1 : 7 ⊺ ​とq 2 \mathbf{q}_2 q 2 ​の乗算により、「want」のベクトル表現を他のすべての入力ベクトル表現「I」、「to」、「buy」、「a」、「car」、「EOS」と比較し、自己注意ウェイトは他の入力ベクトル表現x ′ j , j ≠ 2 \mathbf{x’}_j \text{, with } j \ne 2 x ′ j ​ , with j  = 2に対応して「want」の洗練された表現x ′ ′ 2 \mathbf{x”}_2 x ′ ′ 2 ​の重要性を反映します。

双方向自己注意層の意味をさらに理解するために、次の文が処理されると仮定してみましょう。「The house is beautiful and well located in the middle of the city where it is easily accessible by public transport」。単語「it」は「house」を12つ先に参照しています。Transformerベースのエンコーダでは、双方向自己注意層は「house」の入力ベクトルを「it」の入力ベクトルと関連付けるために1回の数学的操作を実行します（このセクションの最初の図と比較してください）。一方、RNNベースのエンコーダでは、12つ先にある単語は少なくとも12回の数学的操作が必要であり、RNNベースのエンコーダでは線形数の数学的操作が必要です。これにより、RNNベースのエンコーダは長距離の文脈的表現を効果的にモデル化するのが非常に困難になります。また、Transformerベースのエンコーダは、エンコーディングのシーケンス長が同じままであるため、重要な情報を失う可能性がRNNベースのエンコーダデコーダモデルよりもはるかに低いことがわかります。すなわち、len ( X 1 : n ) = len ( X ‾ 1 : n ) = n \textbf{len}(\mathbf{X}_{1:n}) = \textbf{len}(\mathbf{\overline{X}}_{1:n}) = n len ( X 1 : n ​ ) = len ( X 1 : n ​ ) = nであり、一方、RNNは長さを ∗ len ( ( X 1 : n ) = n *\textbf{len}((\mathbf{X}_{1:n}) = n ∗ len ( ( X 1 : n ​ ) = nからlen ( c ) = 1 \textbf{len}(\mathbf{c}) = 1 len ( c ) = 1に圧縮するため、RNNは入力単語間の長距離依存関係を効果的にエンコードするのが非常に困難です。

長距離の依存関係をより簡単に学習できるようにするだけでなく、Transformerアーキテクチャはテキストを並列に処理することができることがわかります。数学的には、自己注意の式をクエリ、キー、値の行列の積として書くことで簡単に示すことができます：

X ′ ′ 1 : n = V 1 : n Softmax ( Q 1 : n ⊺ K 1 : n ) + X ′ 1 : n .

出力 X ′ ′ 1 : n = x ′ ′ 1 , … , x ′ ′ n は、行列の積とSoftmax演算を介して計算され、効果的に並列化することができます。RNNベースのエンコーダモデルでは、隠れ状態 c の計算を逐次的に行う必要があります：最初の入力ベクトル x 1 の隠れ状態を計算し、2番目の入力ベクトルの隠れ状態を計算します。RNNの逐次的な性質は、効果的な並列化を妨げ、現代のGPUハードウェア上のTransformerベースのエンコーダモデルと比較して効率がはるかに低くなります。

さて、トランスフォーマーベースのエンコーダモデルが長距離の文脈表現を効果的にモデル化する方法と、長い入力ベクトルのシーケンスを効率的に処理する方法について、より良い理解を持つはずです。

さあ、MarianMT エンコーダ・デコーダモデルのエンコーダ部分の短い例をコーディングして、説明された理論が実際に成り立つことを確認しましょう。

---

1 {}^1 1 トランスフォーマーベースのモデルにおける前向き層の役割の詳細な説明は、このノートブックの範囲外です。Yun et. al. (2017) では、前向き層が各文脈ベクトル x ′ i を個別に所望の出力空間にマッピングするために重要であると主張されていますが、自己注意層だけではそれを実現できません。ここで注意すべきは、各出力トークン x ′ が同じ前向き層で処理されることです。詳細については、論文を読むことをお勧めします。

2 {}^2 2 ただし、EOSの入力ベクトルを入力シーケンスに追加する必要はありませんが、多くの場合性能を向上させることが示されています。Transformerベースのデコーダの0番目のBOSターゲットベクトルは、最初のターゲットベクトルを予測するための開始入力ベクトルとして必要です。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

embeddings = model.get_input_embeddings()

# create ids of encoded input vectors
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# pass input_ids to encoder
encoder_hidden_states = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state

# change the input slightly and pass to encoder
input_ids_perturbed = tokenizer("I want to buy a house", return_tensors="pt").input_ids
encoder_hidden_states_perturbed = model.base_model.encoder(input_ids_perturbed, return_dict=True).last_hidden_state

# compare shape and encoding of first vector
print(f"Length of input embeddings {embeddings(input_ids).shape[1]}. Length of encoder_hidden_states {encoder_hidden_states.shape[1]}")

# compare values of word embedding of "I" for input_ids and perturbed input_ids
print("Is encoding for `I` equal to its perturbed version?: ", torch.allclose(encoder_hidden_states[0, 0], encoder_hidden_states_perturbed[0, 0], atol=1e-3))

出力:

    入力埋め込みの長さ 7。エンコーダの隠れ状態の長さ 7
    "I" のエンコードは変更されたバージョンと等しいですか？:  False

入力単語の埋め込みの長さ、つまり X 1 : n \mathbf{X}_{1:n} X 1 : n ​ に対応する encoder_hidden_states の長さ、つまり X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ の長さを比較します。また、単語列 “I want to buy a car” とわずかに変更されたバージョン “I want to buy a house” をエンコーダを通過させて、入力シーケンスの最後の単語のみが変更された場合に、最初の出力エンコード（”I” に対応）が異なるかどうかを確認します。

予想どおり、入力単語の埋め込みとエンコーダの出力エンコードの長さ、つまり len ( X 1 : n ) \textbf{len}(\mathbf{X}_{1:n}) len ( X 1 : n ​ ) と len ( X ‾ 1 : n ) \textbf{len}(\mathbf{\overline{X}}_{1:n}) len ( X 1 : n ​ ) は等しいです。さらに、入力シーケンスの最後の単語を “car” から “house” に変更した場合、エンコードされた出力ベクトル x ‾ 1 = “I” \mathbf{\overline{x}}_1 = \text{“I”} x 1 ​ = “I” の値が異なることがわかります。ただし、これは双方向の自己注意を理解していれば驚くことではありません。

余談ですが、BERTなどのオートエンコーダモデルは、トランスフォーマーベースのエンコーダモデルとまったく同じアーキテクチャを持っています。オートエンコーダモデルは、このアーキテクチャを利用して、オープンドメインのテキストデータでの大規模な自己教師付きプレトレーニングを行い、任意の単語列を深層の双方向表現にマッピングすることができます。Devlin ら (2018) では、単一のタスク固有の分類層を持つ事前学習済みの BERT モデルが、11 の NLP タスクで SOTA の結果を達成できることを示しています。🤗Transformers のすべてのオートエンコーダモデルはこちらで見つけることができます。

デコーダ

エンコーダ-デコーダのセクションで説明したように、トランスフォーマーベースのデコーダは、文脈化されたエンコーディングシーケンスに対するターゲットシーケンスの条件付き確率分布を定義します:

p θ d e c ( Y 1 : m ∣ X ‾ 1 : n ) , p_{\theta_{dec}}(\mathbf{Y}_{1: m} | \mathbf{\overline{X}}_{1:n}), p θ d e c ​ ​ ( Y 1 : m ​ ∣ X 1 : n ​ ) ,

これはベイズの定理によって、次のターゲットベクトルが文脈化されたエンコーディングシーケンスとすべての前のターゲットベクトルに対する条件付き分布の積に分解されます:

p θ d e c ( Y 1 : m ∣ X ‾ 1 : n ) = ∏ i = 1 m p θ d e c ( y i ∣ Y 0 : i − 1 , X ‾ 1 : n ) . p_{\theta_{dec}}(\mathbf{Y}_{1:m} | \mathbf{\overline{X}}_{1:n}) = \prod_{i=1}^{m} p_{\theta_{dec}}(\mathbf{y}_i | \mathbf{Y}_{0: i-1}, \mathbf{\overline{X}}_{1:n}). p θ d e c ​ ​ ( Y 1 : m ​ ∣ X 1 : n ​ ) = i = 1 ∏ m ​ p θ d e c ​ ​ ( y i ​ ∣ Y 0 : i − 1 ​ , X 1 : n ​ ) .

まず、トランスフォーマーベースのデコーダが確率分布をどのように定義するかを理解しましょう。トランスフォーマーベースのデコーダは、デコーダブロックのスタックに続いて、”LM ヘッド” と呼ばれる密な層で構成されています。デコーダブロックのスタックは、文脈化されたエンコーディングシーケンス X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ と、BOS \text{BOS} BOS ベクトルで先頭に追加され、最後のターゲットベクトルに切り取られたターゲットベクトルシーケンス、すなわち Y 0 : i − 1 \mathbf{Y}_{0:i-1} Y 0 : i − 1 ​ を、エンコードされたターゲットベクトルのシーケンス Y ‾ 0 : i − 1 \mathbf{\overline{Y}}_{0: i-1} Y 0 : i − 1 ​ にマッピングします。次に、”LM ヘッド” は、エンコードされたターゲットベクトルのシーケンス Y ‾ 0 : i − 1 \mathbf{\overline{Y}}_{0: i-1} Y 0 : i − 1 ​ を、ロジットベクトルのシーケンス L 1 : n = l 1 , … , l n \mathbf{L}_{1:n} = \mathbf{l}_1, \ldots, \mathbf{l}_n L 1 : n ​ = l 1 ​ , … , l n ​ にマッピングします。ここで、各ロジットベクトル l i \mathbf{l}_i l i ​ の次元は語彙のサイズに対応しています。この方法により、各 i ∈ { 1 , … , n } i \in \{1, \ldots, n\} i ∈ { 1 , … , n } に対して、l i \mathbf{l}_i l i ​ 上でのソフトマックス演算を適用することで、語彙全体にわたる確率分布が得られます。これらの分布は条件付き分布を定義します。

p θ d e c ( y i ∣ Y 0 : i − 1 , X ‾ 1 : n ) , ∀ i ∈ { 1 , … , n } ,

それぞれの “LMヘッド” は、しばしば単語埋め込み行列の転置に結びつけられます、つまり、W emb ⊺ = [ y 1 , … , y vocab ] ⊺ 1 {}^1 1 です。直感的には、すべての i ∈ { 0 , … , n − 1 } について、”LMヘッド” レイヤーは符号化された出力ベクトル y ‾ i を語彙のすべての単語埋め込み y 1 , … , y vocab と比較し、対数ベクトル l i + 1 は符号化された出力ベクトルと各単語埋め込みとの類似スコアを表します。softmax操作は、単に類似スコアを確率分布に変換します。各 i ∈ { 1 , … , n } について、次の式が成り立ちます：

p θ d e c ( y ∣ X ‾ 1 : n , Y 0 : i − 1 ) = Softmax ( f θ dec ( X ‾ 1 : n , Y 0 : i − 1 ) ) = Softmax ( W emb ⊺ y ‾ i − 1 ) = Softmax ( l i ) .

これらをすべてまとめると、ターゲットベクトルシーケンス Y 1 : m の条件付き分布をモデル化するために、特別なBOSベクトル、つまり y 0 を前に付けたターゲットベクトル Y 1 : m − 1 と文脈化された符号化シーケンス X ‾ 1 : n を、ログ体ベクトルシーケンス L 1 : m にマッピングします。したがって、各ログ体ターゲットベクトル l i はsoftmax操作を使用して、ターゲットベクトル y i の条件付き確率分布に変換されます。最後に、すべてのターゲットベクトル y 1 , … , y m の条件付き確率を掛け合わせて、完全なターゲットベクトルシーケンスの条件付き確率を得ます：

p θ d e c (Y_{1:m} | \overline{X}_{1:n}) = \prod_{i=1}^m p θ d e c (y_i | Y_{0:i-1}, \overline{X}_{1:n}).

transformer ベースのエンコーダーとは対照的に、transformer ベースのデコーダーでは、エンコードされた出力ベクトル \overline{y}_i は次のターゲットベクトル y_{i+1} の良い表現であるべきであり、入力ベクトル自体の表現ではないことが求められます。さらに、エンコードされた出力ベクトル \overline{y}_i はすべての文脈化されたエンコーディングシーケンス \overline{X}_{1:n} に依存する必要があります。これらの要件を満たすために、各デコーダーブロックには単方向のセルフアテンション層、クロスアテンション層、および2つのフィードフォワード層が含まれています。単方向のセルフアテンション層では、入力ベクトル \mathbf{y’}_j それぞれが、すべての前の入力ベクトル \mathbf{y’}_i (ただし、i ≤ j) との関連性を持ち、次のターゲットベクトルの確率分布モデリングを行います。クロスアテンション層では、各入力ベクトル \mathbf{y”}_j は、文脈化されたエンコーディングベクトル \overline{X}_{1:n} すべてと関連付けられ、エンコーダーの入力に対しても次のターゲットベクトルの確率分布を条件付ける役割を果たします。

では、英語からドイツ語への翻訳の例で transformer ベースのデコーダーを可視化してみましょう。

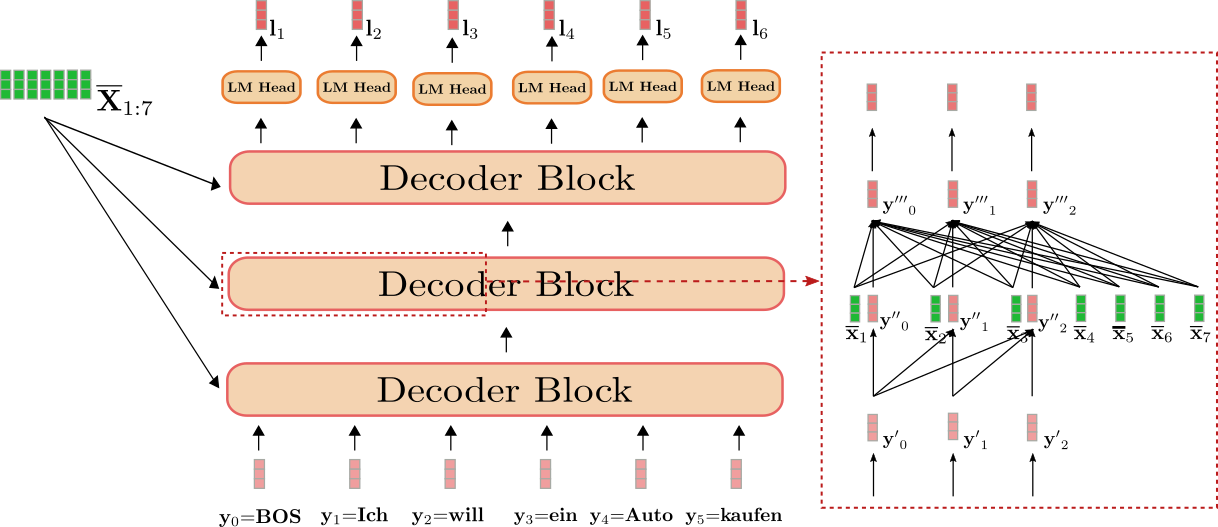
この図では、デコーダーは入力の “BOS”, “Ich”, “will”, “ein”, “Auto”, “kaufen”（薄い赤色で表示）と文脈化されたシーケンス “I”, “want”, “to”, “buy”, “a”, “car”, “EOS”、つまり \overline{X}_{1:7}（濃い緑で表示）を、ロジットベクトル L_{1:6}（濃い赤で表示）にマッピングしています。

各 l_1, l_2, \ldots, l_5 に softmax 操作を適用することで、条件付き確率分布を定義できます:

p θ d e c (y | BOS, \overline{X}_{1:7}), p θ d e c (y | BOS Ich, \overline{X}_{1:7}), p θ d e c (y | BOS Ich will ein Auto kaufen, \overline{X}_{1:7}).

全体的な条件付き確率は以下のように計算できます:

p θ d e c ( Ich will ein Auto kaufen EOS ∣ X ‾ 1 : n )

したがって、次の積として計算できます:

p θ d e c ( Ich ∣ BOS , X ‾ 1 : 7 ) × … × p θ d e c ( EOS ∣ BOS Ich will ein Auto kaufen , X ‾ 1 : 7 ) .

右側の赤いボックスは、最初の3つのターゲットベクトル y 0 , y 1 , y 2 のためのデコーダーブロックを示しています。下部では、単方向のセルフアテンションメカニズムが説明され、中央ではクロスアテンションメカニズムが説明されています。まず、単方向のセルフアテンションに焦点を当てましょう。

バイダイレクショナルセルフアテンションと同様に、単方向のセルフアテンションでは、クエリベクトル q 0 , … , q m − 1 (下の紫色で表示)、キーベクトル k 0 , … , k m − 1 (下のオレンジ色で表示)、およびバリューベクトル v 0 , … , v m − 1 (下の青色で表示) がそれぞれの入力ベクトル y ′ 0 , … , y ′ m − 1 (下の薄い赤色で表示) から射影されます。ただし、単方向のセルフアテンションでは、各クエリベクトル q i は、その対応するキーベクトルおよびそれ以前のキーベクトル k 0 , … , k i とのみ比較され、対応するアテンション重みが生成されます。これにより、出力ベクトル y ′ ′ j (下の濃い赤色で表示) には、後続の入力ベクトル y i (ただし、i > j) に関する情報は含まれません。バイダイレクショナルセルフアテンションと同様に、アテンション重みはそれぞれのバリューベクトルと乗算され、合計されます。

単方向のセルフアテンションは次のように要約できます:

y ′ ′ i = V 0 : i Softmax ( K 0 : i ⊺ q i ) + y ′ i .

キーおよび値のベクトルのインデックス範囲は、0 : i 0:i 0 : i ではなく、0 : m − 1 0: m-1 0 : m − 1 となります。これは、双方向のセルフアテンションにおけるキーベクトルの範囲です。

上記の例では、入力ベクトル y ′ 1 \mathbf{y’}_1 y ′ 1 ​ の単方向のセルフアテンションを説明します。

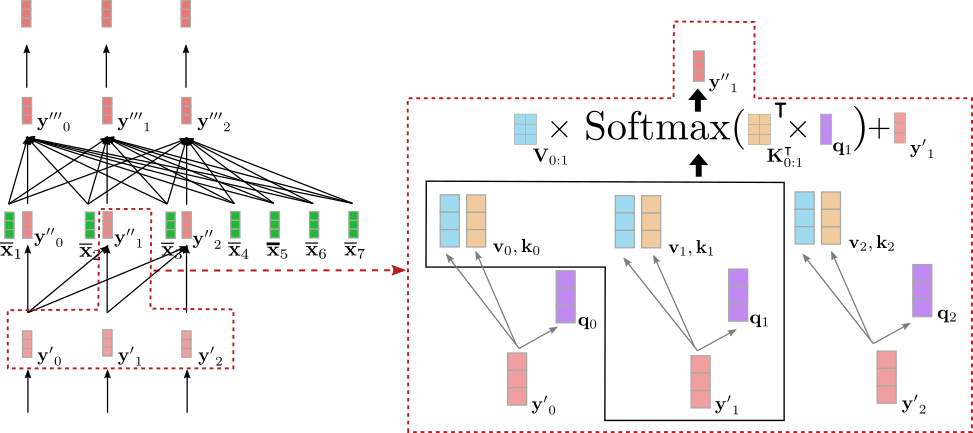
y ′ ′ 1 \mathbf{y”}_1 y ′ ′ 1 ​ は、y ′ 0 \mathbf{y’}_0 y ′ 0 ​ および y ′ 1 \mathbf{y’}_1 y ′ 1 ​ のみに依存します。したがって、単語「Ich」のベクトル表現である y ′ 1 \mathbf{y’}_1 y ′ 1 ​ をそれ自身と「BOS」ターゲットベクトルである y ′ 0 \mathbf{y’}_0 y ′ 0 ​ と関連付けますが、「will」という単語のベクトル表現である y ′ 2 \mathbf{y’}_2 y ′ 2 ​ とは関連付けません。

では、デコーダで双方向のセルフアテンションではなく単方向のセルフアテンションを使用することがなぜ重要なのでしょうか？上述のように、トランスフォーマーベースのデコーダは、入力ベクトルのシーケンス Y 0 : m − 1 \mathbf{Y}_{0: m-1} Y 0 : m − 1 ​ を、次のデコーダ入力ベクトルであるロジットにマッピングします。つまり、L 1 : m \mathbf{L}_{1:m} L 1 : m ​ にマッピングします。この例では、たとえば、入力ベクトル y 1 \mathbf{y}_1 y 1 ​ = “Ich” は、ロジットベクトル l 2 \mathbf{l}_2 l 2 ​ にマッピングされ、それは次に入力ベクトル y 2 \mathbf{y}_2 y 2 ​ を予測するために使用されます。したがって、y ′ 1 \mathbf{y’}_1 y ′ 1 ​ が次の入力ベクトル Y ′ 2 : 5 \mathbf{Y’}_{2:5} Y ′ 2 : 5 ​ にアクセスできる場合、デコーダは単に “will” のベクトル表現である y ′ 2 \mathbf{y’}_2 y ′ 2 ​ を出力の y ′ ′ 1 \mathbf{y”}_1 y ′ ′ 1 ​ にコピーします。これは最後の層に転送され、符号化された出力ベクトル y ‾ 1 \mathbf{\overline{y}}_1 y ‾ 1 ​ は、本質的にベクトル表現 y 2 \mathbf{y}_2 y 2 ​ に対応します。

これは明らかに不利です。トランスフォーマーベースのデコーダは、すべての前の単語を与えられた場合に次の単語を予測することを学ぶのではなく、単にターゲットベクトル y i \mathbf{y}_i y i ​ をネットワークを通じて y ‾ i − 1 \mathbf{\overline{y}}_{i-1} y ‾ i − 1 ​ にコピーします（ただし、i ∈ { 1 , … , m } i \in \{1, \ldots, m \} i ∈ { 1 , … , m } の場合）。次のターゲットベクトルの条件付き分布を定義するためには、分布は次のターゲットベクトル自体に依存できません。ターゲットベクトルをモデル化するために p ( y ∣ Y 0 : i , X ‾ ) p(\mathbf{y} | \mathbf{Y}_{0:i}, \mathbf{\overline{X}}) p ( y ∣ Y 0 : i ​ , X ) から y i \mathbf{y}_i y i ​ を予測することはあまり意味がありません。その分布は、モデル化するターゲットベクトルに条件付けられているからです。したがって、単方向のセルフアテンションアーキテクチャを使用することで、次のターゲットベクトルの条件付き分布を効果的にモデル化するための因果関係のある確率分布を定義することができます。

素晴らしい！では、エンコーダとデコーダを接続するレイヤーであるクロスアテンションメカニズムに移ることができます！

クロスアテンションレイヤーは、2つのベクトルシーケンスを入力として受け取ります。単方向のセルフアテンションレイヤーの出力である Y ′ ′ 0 : m − 1 \mathbf{Y”}_{0: m-1} Y ′ ′ 0 : m − 1 ​ と文脈化されたエンコーディングベクトル X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ です。セルフアテンションレイヤーと同様に、クエリベクトル q 0 , … , q m − 1 \mathbf{q}_0, \ldots, \mathbf{q}_{m-1} q 0 ​ , … , q m − 1 ​ は、前のレイヤーの出力ベクトルである Y ′ ′ 0 : m − 1 \mathbf{Y”}_{0: m-1} Y ′ ′ 0 : m − 1 ​ の射影です。ただし、キーベクトル k 0 , … , k m − 1 \mathbf{k}_0, \ldots, \mathbf{k}_{m-1} k 0 ​ , … , k m − 1 ​ および値ベクトル v 0 , … , v m − 1 \mathbf{v}_0, \ldots, \mathbf{v}_{m-1} v 0 ​ , … , v m − 1 ​ は、文脈化されたエンコーディングベクトル X ‾ 1 : n \mathbf{\overline{X}}_{1:n} X 1 : n ​ の射影です。キー、値、およびクエリベクトルを定義した後、クエリベクトル q i \mathbf{q}_i q i ​ はすべてのキーベクトルと比較され、対応するスコアはそれぞれの値ベクトルに重み付けされます。これは双方向のセルフアテンションと同様で、すべての i ∈ 0 , … , m − 1 i \in \{0, \ldots, m-1\} i ∈ 0 , … , m − 1 に対して出力ベクトル y ′ ′ ′ i \mathbf{y”’}_i y ′ ′ ′ i ​ を与えます。クロスアテンションは次のように要約できます：

y ′ ′ ′ i = V 1 : n Softmax ( K 1 : n ⊺ q i ) + y ′ ′ i.

上記の例における入力ベクトル y ′ ′ 1 のクロスアテンション機構を可視化しましょう。

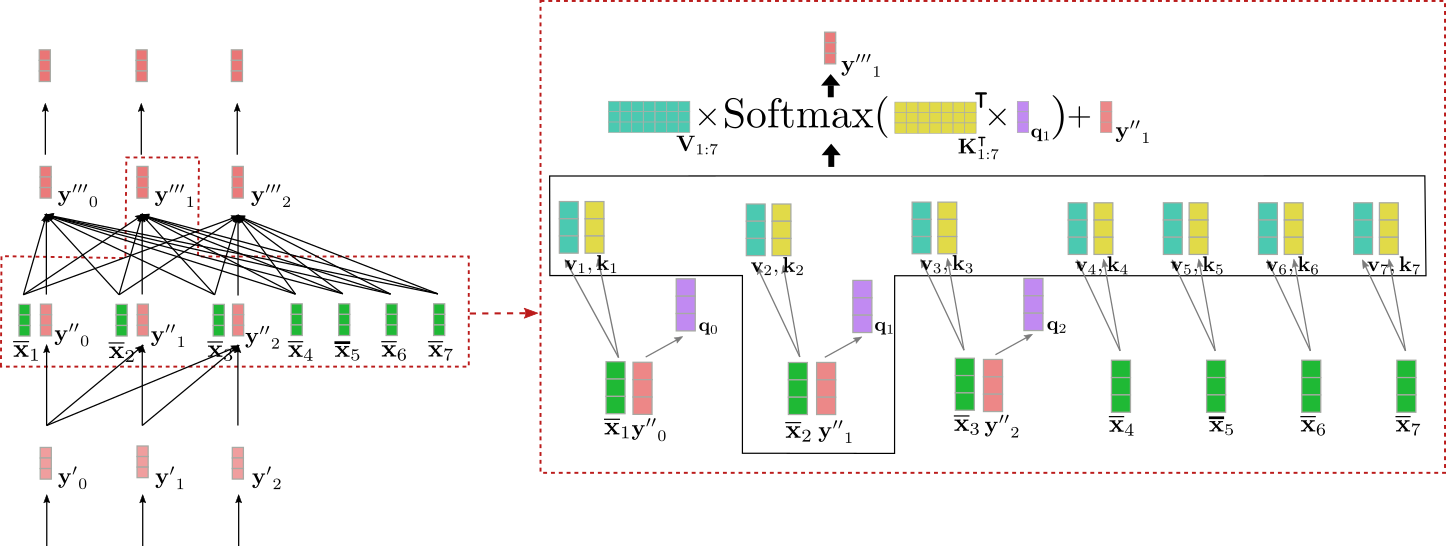
この図から、クエリベクトル q 1（紫色で表示されています）は y ′ ′ 1（赤色で表示されています）から派生しており、したがって単語「Ich」のベクトル表現に依存しています。クエリベクトル q 1 は、エンコーダのすべての入力ベクトル X 1 : n（黄色で表示されている）に対応するコンテキストエンコーディング表現のキーベクトル k 1、…、k 7（黄色で表示されている）と比較されます。X 1 : n は “I want to buy a car EOS” です。これにより、単語「Ich」のベクトル表現がエンコーダのすべての入力ベクトルと直接関係しています。最後に、アテンションの重みは値ベクトル v 1、…、v 7（ターコイズで表示されている）と乗算され、入力ベクトル y ′ ′ 1 に加えて出力ベクトル y ′ ′ ′ 1（濃赤色で表示されている）を生成します。

では、直感的には何が起こっているのでしょうか？各出力ベクトル y ′ ′ ′ i は、エンコーダのすべての入力ベクトルの値ベクトルの重み付き和であり、入力ベクトル y ′ ′ i 自体（上記の式を参照）も含まれます。理解するためのキーとなるメカニズムは次のとおりです。入力デコーダベクトル q i のクエリ射影がエンコーダ入力ベクトル k j のキー射影にどれだけ似ているかによって、エンコーダ入力ベクトル v j の値射影の重要性が決まります。大まかに言えば、デコーダの入力表現がエンコーダの入力表現にどれだけ「関連している」かによって、入力表現がデコーダの出力表現にどれだけ影響を与えるかが決まります。

素晴らしいですね！このアーキテクチャは、エンコーダの入力ベクトル X ‾ 1 : n と入力ベクトル y ′ ′ i の相互作用に基づいて、各出力ベクトル y ′ ′ ′ i を条件づける素晴らしいものです。重要な観察点として、このアーキテクチャは、出力ベクトル y ′ ′ ′ i が条件づけられるコンテキストエンコーディングベクトル X ‾ 1 : n の数 n に完全に依存していないことが挙げられます。キーベクトル k 1、…、k n と値ベクトル v 1、…、v n を導出するためのすべての射影行列 W k cross および W v cross は、位置 1、…、n のすべての位置と値ベクトル v 1、…、v n で共有されます。さらに、値ベクトル v 1、…、v n は、単一の重み付け平均ベクトルに合計されます。このアーキテクチャは、トランスフォーマベースのデコーダがRNNベースのデコーダの長距離依存性の問題に悩まされない理由も明らかになります。デコーダの各ロジットベクトルは、エンコーダの各出力ベクトルに直接依存しているため、最初のエンコードされた出力ベクトルと最後のデコーダのロジットベクトルを比較するための数学的操作の数は、基本的には1つだけです。

結論として、単方向のセルフアテンションレイヤーは、各出力ベクトルを全ての前のデコーダー入力ベクトルと現在の入力ベクトルに条件付ける役割を担い、クロスアテンションレイヤーは、各出力ベクトルをさらに全てのエンコードされた入力ベクトルに条件付ける役割を担います。

理論的な理解を検証するために、エンコーダーのセクションでのコード例を続けましょう。

---

1 {}^1 1 単語の埋め込み行列 W emb \mathbf{W}_{\text{emb}} W emb ​ は、各入力単語に一意の文脈非依存のベクトル表現を与えます。この行列は通常、「LM Head」レイヤーとして固定されています。ただし、「LM Head」レイヤーは、完全に独立した「エンコードされたベクトルからロジットへの重みマッピング」で構成される場合もあります。

2 {}^2 2 トランスフォーマーベースのモデルにおいて、フィードフォワード層が果たす役割の詳細な説明は、このノートブックの範囲外です。フィードフォワード層は、自己アテンションレイヤーだけでは行うことができない各文脈ベクトル x ′ i \mathbf{x’}_i x ′ i ​ を所望の出力空間に個別にマッピングするために重要であると、Yun et. al, (2017) では主張されています。ここで注意すべきは、各出力トークン x ′ \mathbf{x’} x ′ は同じフィードフォワード層によって処理されるということです。詳細については、論文をお読みいただくことをお勧めします。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")
embeddings = model.get_input_embeddings()

# エンコーダー入力のためのトークンIDを作成
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# エンコーダーに入力トークンIDを渡す
encoder_output_vectors = model.base_model.encoder(input_ids, return_dict=True).last_hidden_state

# デコーダー入力のためのトークンIDを作成
decoder_input_ids = tokenizer("<pad> Ich will ein", return_tensors="pt", add_special_tokens=False).input_ids

# デコーダーにデコーダー入力のトークンIDとエンコードされた入力ベクトルを渡す
decoder_output_vectors = model.base_model.decoder(decoder_input_ids, encoder_hidden_states=encoder_output_vectors).last_hidden_state

# デコーダーの出力と埋め込みの重みを掛け合わせて埋め込みを求める
lm_logits = torch.nn.functional.linear(decoder_output_vectors, embeddings.weight, bias=model.final_logits_bias)

# デコーダーの入力を少し変更する
decoder_input_ids_perturbed = tokenizer("<pad> Ich will das", return_tensors="pt", add_special_tokens=False).input_ids
decoder_output_vectors_perturbed = model.base_model.decoder(decoder_input_ids_perturbed, encoder_hidden_states=encoder_output_vectors).last_hidden_state
lm_logits_perturbed = torch.nn.functional.linear(decoder_output_vectors_perturbed, embeddings.weight, bias=model.final_logits_bias)

# 最初のベクトルの形状とエンコーディングを比較する
print(f"デコーダーの入力ベクトルの形状 {embeddings(decoder_input_ids).shape}。デコーダーのロジットの形状 {lm_logits.shape}")

# "I" の単語埋め込みの値を input_ids と perturbed input_ids の間で比較する
print("「Ich」のエンコーディングは変更されたバージョンと等しいですか？: ", torch.allclose(lm_logits[0, 0], lm_logits_perturbed[0, 0], atol=1e-3))

出力:

    デコーダーの入力ベクトルの形状 torch.Size([1, 5, 512])。デコーダーのロジットの形状 torch.Size([1, 5, 58101])
    「Ich」のエンコーディングは変更されたバージョンと等しいですか？:  True

デコーダーの入力単語埋め込みの出力形状、つまり embeddings(decoder_input_ids)（Y 0 : 4 \mathbf{Y}_{0: 4} Y 0 : 4 ​ に対応し、ここで <pad> は BOS を表し、「Ich will das」は4つのトークンにトークン化されています）と lm_logits（L 1 : 5 \mathbf{L}_{1:5} L 1 : 5 ​ に対応）の次元を比較します。また、単語のシーケンス「 <pad> Ich will ein」とわずかに変更されたバージョン「 <pad> Ich will das」を encoder_output_vectors と一緒にデコーダーに渡して、入力シーケンスの最後の単語だけが変更された場合（”ein” -> “das”）に、2番目の lm_logit が異なるかどうかを確認します。

デコーダーの入力単語埋め込みとlm_logitsの出力形状、つまりY 0 : 4 \mathbf{Y}_{0: 4} Y 0 : 4 ​とL 1 : 5 \mathbf{L}_{1:5} L 1 : 5 ​の次元は、最後の次元で異なります。シーケンスの長さは同じです (=5)が、デコーダーの入力単語埋め込みの次元はmodel.config.hidden_sizeに対応し、lm_logitsの次元は語彙サイズmodel.config.vocab_sizeに対応します。これは前述の通りです。また、エンコードされた出力ベクトルのl 1 = “Ich” \mathbf{l}_1 = \text{“Ich”} l 1 ​ = “Ich”の値は、最後の単語が”ein”から”das”に変わった場合でも同じです。これは、単方向の自己注意を理解している場合には驚くことではありません。

最後に、GPT2などの自己回帰モデルは、エンコーダーの出力に依存していない単独の自己回帰モデルを除くと、トランスフォーマベースのデコーダーモデルと同じアーキテクチャを持っています。もしクロスアテンション層を削除するならば、自己回帰モデルはエンコーダーの出力に依存していません。したがって、自己回帰モデルは基本的には自己符号化モデルと同じですが、双方向の注意を単方向の注意に置き換えます。これらのモデルは、大規模なオープンドメインのテキストデータで事前学習することもでき、自然言語生成（NLG）タスクで印象的な性能を示すことができます。Radford et al.（2019）では、事前学習済みのGPT2モデルが微調整せずにさまざまなNLGタスクでSOTAまたはほぼSOTAの結果を達成できることを示しています。🤗Transformersのすべての自己回帰モデルはここで見つけることができます。

以上です！これで、トランスフォーマベースのエンコーダーデコーダーモデルとそれらを🤗Transformersライブラリで使用する方法について理解を深めることができました。

貴重なフィードバックをくれたVictor Sanh、Sasha Rush、Sam Shleifer、Oliver Åstrand、Ted Moskovitz、Kristian Kyvikに多くの感謝を申し上げます。

付録

上記の説明にもあるように、次のコードスニペットは、トランスフォーマベースのエンコーダーデコーダーモデルの単純な生成メソッドをプログラムする方法を示しています。ここでは、torch.argmaxを使用してターゲットベクトルをサンプリングする単純な貪欲デコーディングメソッドを実装しています。

from transformers import MarianMTModel, MarianTokenizer
import torch

tokenizer = MarianTokenizer.from_pretrained("Helsinki-NLP/opus-mt-en-de")
model = MarianMTModel.from_pretrained("Helsinki-NLP/opus-mt-en-de")

# エンコードされた入力ベクトルのidを作成
input_ids = tokenizer("I want to buy a car", return_tensors="pt").input_ids

# BOSトークンを作成
decoder_input_ids = tokenizer("<pad>", add_special_tokens=False, return_tensors="pt").input_ids

assert decoder_input_ids[0, 0].item() == model.config.decoder_start_token_id, "`decoder_input_ids` should correspond to `model.config.decoder_start_token_id`"

# STEP 1

# input_idsをエンコーダーとデコーダーに渡し、デコーダーにBOSトークンを渡して最初のロジットを取得する
outputs = model(input_ids, decoder_input_ids=decoder_input_ids, return_dict=True)

# エンコードされたシーケンスを取得
encoded_sequence = (outputs.encoder_last_hidden_state,)
# ロジットを取得
lm_logits = outputs.logits

# 最も確率が高い最後のトークンをサンプリングする
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)

# 結合する
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# STEP 2

# エンコードされた入力とBOS + "Ich"をデコーダーに渡して2番目のロジットを取得する
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits

# 再び最も確率が高い最後のトークンをサンプリングする
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)

# 再び結合する
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# STEP 3
lm_logits = model(None, encoder_outputs=encoded_sequence, decoder_input_ids=decoder_input_ids, return_dict=True).logits
next_decoder_input_ids = torch.argmax(lm_logits[:, -1:], axis=-1)
decoder_input_ids = torch.cat([decoder_input_ids, next_decoder_input_ids], axis=-1)

# これまでに生成されたものを確認しましょう！
print(f"これまでに生成されたもの： {tokenizer.decode(decoder_input_ids[0], skip_special_tokens=True)}")

# これはループでも書くことができます。

出力:

    生成されたもの: Ich will ein

このコード例では、先ほど説明した内容を正確に示しています。入力として「I want to buy a car」とBOSトークンをエンコーダ・デコーダモデルに渡し、最初のロジットl1（つまり、最初のlm_logitsの行）からサンプリングします。ここでのサンプリング戦略は単純であり、最も高い確率を持つ次のデコーダ入力ベクトルを貪欲に選択します。自己回帰的に、サンプリングされたデコーダ入力ベクトルを前の入力と共にエンコーダ・デコーダモデルに渡し、再度サンプリングします。これを3回繰り返します。その結果、「Ich will ein」という単語が生成されました。結果は完璧です – これは入力の正しい翻訳の始まりです。

実際には、lm_logitsをサンプリングするためにより複雑なデコーディング手法が使用されます。これについては、このブログ記事で詳しく説明しています。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!