「Transformerの簡略化：あなたが理解する言葉を使った最先端のNLP — part 3 — アテンション」

Transformerの簡略化：最先端のNLPに理解しやすい言葉を使ったアテンションの説明

LLMsのコアテクニックであるアテンションの詳細

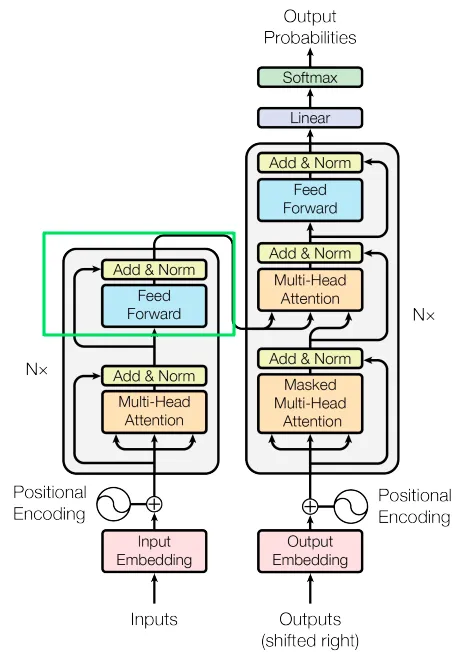
トランスフォーマーは、AIの分野、そしておそらく世界全体において重大な影響を与えています。このアーキテクチャはいくつかのコンポーネントで構成されていますが、元の論文が「Attention is All You Need」という名前であることから、アテンションメカニズムが特に重要であることは明らかです。このシリーズの第3部では、主にアテンションとそれに関連する機能に焦点を当て、トランスフォーマーのフィルハーモニックがうまく演奏されるようにします。

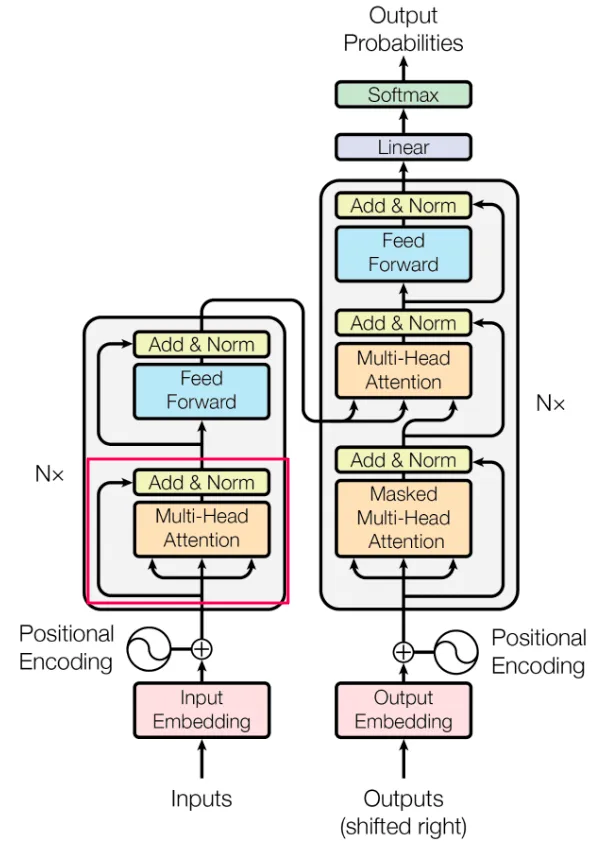
アテンション

トランスフォーマーの文脈では、アテンションはモデルが処理中に入力の関連する部分に焦点を当てる仕組みを指します。文章の特定の部分に光を当てる懐中電灯のようなもので、文脈に応じて重要度を付けることができます。定義よりも例が効果的であると考えています。なぜなら、例は脳を鍛えるパズルのようなものであり、脳に隙間を埋めるための可能性を提供し、概念を自ら理解することができるからです。

例えば、「The man took the chair and disappeared」という文が与えられた場合、自然に文の異なる部分に対して異なる重要度（アテンション）を割り当てます。驚くべきことに、特定の単語を削除しても、意味はほぼそのままです。「man took chair disappeared」というバージョンは壊れた英語ですが、元の文と比べてもメッセージの本質を理解することができます。興味深いことに、この文の単語のうち「The」「the」「and」の3つの単語は文中の単語の43%を占めていますが、全体的な意味にはほとんど貢献していません。この観察は、ベルリンで私の素晴らしいドイツ語に出くわしたすべてのベルリナーには明らかだったかもしれません（ドイツ語を学ぶか幸せになるか、それはあなたが選ぶ決断です）、しかしMLモデルにはそれほど明確ではありません。

過去には、再帰ニューラルネットワーク（RNN）などの以前のアーキテクチャは、入力シーケンスの遥か以前に現れる単語を「覚える」ことに苦労しました。既にご存知のように、これらのモデルは基本的に数学的な操作を使用してデータを処理します。残念ながら、以前のアーキテクチャで使用されていた数学的な操作は、遠い未来のシーケンスに十分に単語の表現を保持するために効率的ではありませんでした。

• 「非構造化データ内のデータスライスの検出」 翻訳結果は以下の通りです： 「非構造化データ内でデータスライスを見つける」
• 「グラフデータベースを使用してリアルタイムの推薦エンジンを構築する方法」
• 統計学における変数の多様性：データ専門家のためのガイド

この長期依存性の制限により、RNNは文脈情報を長期間にわたって維持する能力が制約され、言語翻訳や感情分析などのタスクに影響を与えました。しかし、アテンションメカニズムと自己アテンションメカニズムを持つトランスフォーマーは、この問題により効果的に対処しています。トランスフォーマーは、入力の遠い距離にわたる依存関係を効率的に捉えることができ、シーケンスの遥か以前に現れる単語に対しても文脈と関連性を保持することができます。その結果、トランスフォーマーは以前のアーキテクチャの制約を克服する画期的な解決策となり、さまざまな自然言語処理タスクの性能を大幅に向上させました。

現在私たちが遭遇する高度なチャットボットのような優れた製品を作り出すためには、モデルに高い価値のある単語と低い価値のある単語を区別する能力を備えさせることが重要であり、また入力の遠い距離にわたって文脈情報を維持する必要があります。これらの課題に対処するために、トランスフォーマーアーキテクチャで導入されたメカニズムは「アテンション」として知られています。

※人間は人間同士を区別する技術を非常に長い間開発してきましたが、それらをここでは使用しません。

ドット積

モデルは理論的にどのようにして異なる単語の重要性を判断するのでしょうか？文を分析する際には、お互いとの関係が強い単語を特定することを目指します。単語は数値のベクトルとして表現されるため、数値の類似性を測るための尺度が必要です。ベクトルの類似性を測るための数学的な用語は「ドット積」です。これは、2つのベクトルの要素を掛け合わせてスカラー値（2、16、-4.43など）を生成し、それが彼らの類似性の表現となります。機械学習はさまざまな数学的操作に基づいており、その中でもドット積は特に重要です。そのため、この概念について詳しく説明します。

直感5つの単語「florida」「california」「texas」「politics」「truth」に対して実数の表現（埋め込み）があるとしましょう。埋め込みは単なる数値なので、理論的にはグラフ上にプロットすることができます。ただし、埋め込みの次元数が非常に高い（100から1000までの範囲になることが一般的）ため、そのままの状態ではプロットすることはできません。100次元のベクトルを2次元のコンピューター/携帯電話の画面上にプロットすることはできません。さらに、人間の脳は3次元以上のものを理解するのが難しいです。4次元のベクトルはどのように見えるのでしょうか？わかりません。

この問題を克服するために、私たちは主成分分析（PCA）を利用して次元数を減らす技術を使用します。PCAを適用することで、埋め込みを2次元空間（x、y座標）に射影することができます。この次元の削減により、データをグラフ上で視覚化することができます。削減により一部の情報が失われますが、これらの削減されたベクトルは、元の埋め込みとの十分な類似性を保持していることを期待し、単語間の関係を理解するための洞察を得ることができます。

これらの数字はGloVeの埋め込みに基づいています。

florida = [-2.40062016,  0.00478901]california = [-2.54245794, -0.37579669]texas = [-2.24764634, -0.12963368]politics = [3.02004564,  2.88826688]truth = [4.17067881, -2.38762552]

おそらく、これらの数字にはパターンがあることに気付くかもしれませんが、私たちは数字をプロットして生活を楽にします。

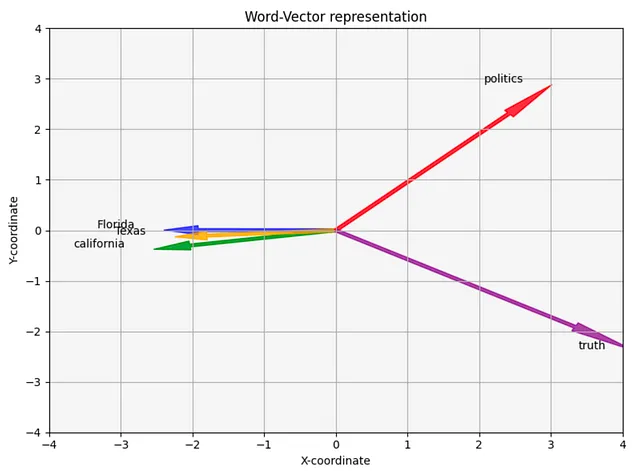
この可視化では、5つの異なる単語を表す5つの2Dベクトル（x、y座標）が表示されます。見ての通り、プロットはいくつかの単語が他の単語と関連していることを示唆しています。

数学ベクトルの可視化の数学的な対応は、簡単な方程式を介して表現することができます。もし数学があまり得意ではなく、「シンプルなネットワークアーキテクチャ」という言葉でTransformersのアーキテクチャを説明する著者の説明を思い出せない場合、MLの人々には奇妙なことが起こるのかもしれません。それはおそらく真実ですが、今回の場合はシンプルです。説明します：

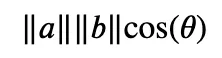
記号||a||はベクトル”a”の大きさを示し、原点（点0,0）とベクトルの先端との距離を表します。大きさの計算は次のようになります：

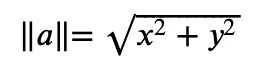
この計算の結果は、4や12.4などの数字です。シータ（θ）はベクトル間の角度を指し、それを可視化で確認してください。シータの余弦、cos(θ)は、その角度に余弦関数を適用した結果です。

コードStanford大学の研究者がGloVeアルゴリズムを使用して実際の単語の埋め込みを生成しました。これらの埋め込みを作成するための特定の技術は異なりますが、前のシリーズの前半で話したのと同じ基本的な概念を持っています。例として、4つの単語を取り、その次元を2に減らし、それから彼らのベクトルを直感的なx座標とy座標としてプロットしました。

このプロセスを正しく機能させるためには、GloVeの埋め込みをダウンロードする必要があります。

*コードの一部、特に最初のボックスは私が見たコードに触発されたものですが、ソースを見つけることができません。

import pandas as pdpath_to_glove_embds = 'glove.6B.100d.txt'glove = pd.read_csv(path_to_glove_embds, sep=" ", header=None, index_col=0)glove_embedding = {key: val.values for key, val in glove.T.items()}

words = ['florida', 'california', 'texas', 'politics', 'truth']word_embeddings = [glove_embedding[word] for word in words]print(word_embeddings[0]).shape # 各単語を表すための100個の数字。---------------------出力:(100,)

pca = PCA(n_components=2) # 次元を100から2に削減.word_embeddings_pca = pca.fit_transform(word_embeddings)

for i in range(5):    print(word_embeddings_pca[i])---------------------出力:[-2.40062016  0.00478901] # florida[-2.54245794 -0.37579669] # california[-2.24764634 -0.12963368] # texas[3.02004564 2.88826688] # politics[ 4.17067881 -2.38762552] # truth

現在、私たちは5つの単語の本物の表現を持っています。次のステップは、ドット積の計算を行うことです。

ベクトルの大きさ：

import numpy as npflorida_vector = [-2.40062016,  0.00478901]florida_vector_magnitude = np.linalg.norm(florida_vector)print(florida_vector_magnitude)---------------------output:2.4006249368060817 # ベクトル「florida」の大きさは2.4です。

2つの似たベクトルのドット積。

import numpy as npflorida_vector = [-2.40062016,  0.00478901]texas_vector = [-2.24764634 -0.12963368]print(np.dot(florida_vector, texas_vector))---------------------output:5.395124299364358

2つの異なるベクトルのドット積。

import numpy as npflorida_vector = [-2.40062016,  0.00478901]truth_vector = [4.17067881, -2.38762552]print(np.dot(florida_vector, truth_vector))---------------------output:-10.023649994662344

ドット積の計算から明らかなように、それは異なる概念の類似性を捉え反映するようです。

スケーラブルドット積注意

直感ドット積を理解したので、アテンションに戻ることができます。特に、セルフアテンションメカニズムです。セルフアテンションを使用することで、モデルは各単語の重要性を決定する能力を得ることができます。単語の「物理的」な近接性に関係なく、各単語の文脈的関連性に基づいて情報を処理し、より良い理解を得ることができます。

この野心的な目標を達成するために、学習可能なパラメータで構成された3つの行列であるクエリ、キー、バリュー（Q、K、V）を作成します。クエリ行列は、ユーザーが問い合わせた単語を含むクエリ行列として想像できます（例えば、chatGPTに「神は今日の午後5時に利用可能ですか？」と尋ねる場合、それがクエリです）。キー行列には、シーケンス内の他のすべての単語が含まれます。これらの行列間のドット積を計算することで、各単語と現在調べている単語との関連度を得ることができます（例えば、クエリの翻訳や回答の生成）。

バリュー行列は、シーケンス内のすべての単語の「クリーンな」表現を提供します。他の2つの行列と同様に構成されるのでなぜ私がそれをクリーンと呼ぶのかというと、バリュー行列は元の形式のままであり、他の行列による乗算やいくつかの値による正規化は行いません。この違いにより、バリュー行列は追加の計算や変換から解放され、元の埋め込みを保持することが保証されます。

すべての3つの行列は、word_embedding（512）のサイズで構築されています。ただし、それらは「ヘッド」と呼ばれる部分に分割されます。論文では8つのヘッドが使用され、それぞれの行列のサイズはsequence_length×64となります。同じ操作をデータの1/8で8回行う理由は、異なるセットの重み（学習可能な）を使用して同じ操作を8回行うことで、データの固有の多様性を利用することができるからです。各ヘッドは入力内の特定の側面に焦点を当てることができ、集計することでパフォーマンスを向上させることができます。

*ほとんどの実装では、実際にはメインの行列を8つに分割しません。分割はインデックスを使用して行われ、各部分に対して並列処理を許可します。ただし、これらは実装の詳細です。理論的には、8つの行列を使用してほぼ同じことができました。

QとKは乗算（ドット積）され、次に次元数の平方根で正規化されます。結果をソフトマックス関数を介して渡し、結果は行列Vと乗算されます。結果を正規化する理由は、QとKはある程度ランダムに生成される行列であるためです。それらの次元は完全に関連していない（独立している）場合があり、独立した行列の乗算は非常に大きな数値を生み出す可能性があります。そのため、非線形変換であるソフトマックスを使用して、すべての数値を0から1の範囲にし、合計が1になるようにします。結果は確率分布に似ています（0から1までの数値が合計で1になるため）。これらの数値は、シーケンス内の各単語の相互関係の重要性を示します。最後に、結果を行列Vと乗算すると、セルフアテンションスコアが得られます。

エンコーダーは実際にはN（論文ではN=6）の同一のレイヤーから構築されており、各レイヤーは前のレイヤーからの入力を受け取り、同じことを行います。最終レイヤーはデコーダー（このシリーズの後半で説明します）およびエンコーダーの上位レイヤーにデータを送信します。

以下はセルフアテンションの可視化です。教室の中の友達グループのようです。一部の人は他の人とよりつながっています。一部の人は誰ともつながっていません。

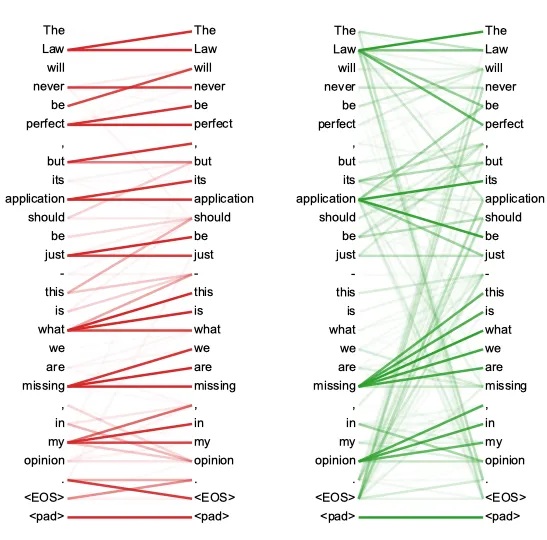
数学 Q、K、V行列は埋め込み行列の線形変換によって導出されます。線形変換は機械学習において重要ですので、ML実践者になる興味がある場合は、さらに探求することをお勧めします。詳細には立ち入りませんが、線形変換はベクトル（または行列）を一つの空間から別の空間に移動する数学的な操作です。複雑に聞こえるかもしれませんが、一つの方向を指す矢印が右に30度移動するイメージです。これが線形変換を示しています。このような操作が線形であるためのいくつかの条件がありますが、今のところそれはあまり重要ではありません。重要なポイントは、線形変換が元のベクトルの多くの特性を保持するということです。

セルフアテンションレイヤーの全体的な計算は、次の式を適用することで行われます：

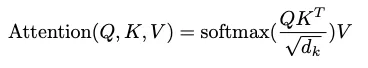
計算プロセスは次のように展開されます：1. QにKの転置（反転）を掛けます。2. 結果を行列Kの次元の平方根で割ります。3. これにより、各単語が他の単語とどれだけ似ているかを示す「アテンション行列スコア」が得られます。各行をソフトマックス（非線形）変換に渡します。ソフトマックスは3つの興味深いことを行います：a. すべての数値を0から1の間にスケーリングします。b. すべての数値を合計して1にします。c. ギャップを強調し、わずかに重要なものを非常に重要にします。その結果、モデルが単語x1とx2、x3、x4などの間の接続をどの程度認識するかを簡単に区別できるようになります。4. スコアにV行列を掛けます。これがセルフアテンション操作の最終結果です。

マスキング

このシリーズの前の章では、文中の特別な出現（文の最初の単語、最後の単語など）を処理するためにダミートークンを使用することを説明しました。これらのトークンの1つである<PADDING>は、実際のデータがないことを示しますが、計算全体の一貫性を保つために行列のサイズを一貫させる必要があります。モデルがこれらがダミートークンであることを理解し、セルフアテンション計算中に考慮されないようにするために、これらのトークンをマイナス無限大（非常に大きな負の数、例えば-153513871339）で表します。マスキング値は、QとKの乗算結果に追加されます。その後、ソフトマックスはこれらの数値を0に変換します。これにより、ダミートークンを効果的に無視しながら計算の整合性を保つことができます。

ドロップアウト

セルフアテンションレイヤーの後にはドロップアウト操作が適用されます。ドロップアウトは機械学習で広く使用される正則化技術です。正則化の目的は、モデルに対してトレーニング中に制約を課し、特定の入力の詳細に過度に依存することを困難にすることです。その結果、モデルはより堅牢に学習し、一般化能力を向上させます。実際の実装では、異なるレイヤーのアクティベーション（異なるレイヤーから出力される数値）のいくつかをランダムに選択し、ゼロにします。同じレイヤーの各パスでは、異なるアクティベーションがゼロにされ、モデルが特定のデータに特化した解を見つけることを防ぎます。要するに、ドロップアウトはモデルが多様な入力を処理し、データの特定のパターンに合わせられるのを困難にするのに役立ちます。

スキップ接続

Transformerアーキテクチャで行われる別の重要な操作は、スキップ接続と呼ばれます。

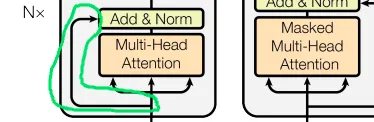
スキップ接続は、入力を変換せずに渡す方法です。例えば、私が上司に報告し、上司がさらに上司に報告するとします。報告をより有用にするための純粋な意図があっても、入力は別の人（またはMLレイヤー）によって処理されるときに変更されます。このアナロジーで言えば、スキップ接続は私が直接上司の上司に報告することになります。その結果、上司は私の上司（処理されたデータ）と私自身（未処理）の両方から入力を受け取ることができます。上司はその結果を活かしてより良い意思決定をすることができるでしょう。スキップ接続を使用する理由は、消失勾配などの潜在的な問題を解決するためです。後続のセクションで説明します。

加算と正規化レイヤー

直感「加算と正規化」レイヤーは、加算と正規化を行います。簡単なので、加算から始めましょう。基本的には、セルフアテンションレイヤーからの出力を元の入力（スキップ接続から受け取ったもの）に加算します。この加算は要素ごとに行われます（各数値は同じ位置の数値と加算されます）。その結果を正規化します。

再度言いますが、正規化する理由は、各レイヤーが多くの計算を行うためです。数値を何度も乗算すると、意図しないシナリオが発生する可能性があります。例えば、0.3のような分数を0.9のような他の分数と乗算すると、元の値よりも小さい0.27が得られます。これを何度も行うと、0に非常に近い値になる可能性があります。このような場合、深層学習において勾配消失と呼ばれる問題が発生する可能性があります。詳細には立ち入りませんが、数値が0に近づくと、モデルは学習できなくなります。現代の機械学習の基礎は、勾配を計算し、それらの勾配を使用して重みを調整することです。勾配が0に近い場合、モデルは効果的に学習することが非常に困難になります。

逆に、非分数の数値が非分数と乗算されると、値が極端に大きくなり、爆発的な勾配と呼ばれる現象が発生することがあります。その結果、重みと活性化の変化が非常に大きくなり、トレーニングプロセス中に不安定性と発散が発生し、モデルの学習が困難になります。

機械学習モデルは、まるで小さな子供のような存在です。数値が極端に大きくなったり小さくなったりすることを防ぐための保護が必要です。その一つの方法が正規化です。

数学正規化レイヤーの操作は恐ろしく見えますが、実際には比較的単純です。

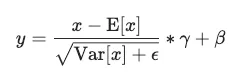
正規化レイヤーの操作では、次の単純な手順を各入力に対して行います：

1. 入力から平均を引きます。
2. 分散の平方根で除算し、ゼロでの除算を避けるために微小な値であるイプシロンを加えます。
3. 得られたスコアに、学習可能なパラメータであるガンマ（γ）を乗算します。
4. 別の学習可能なパラメータであるベータ（β）を加えます。

これらの手順により、平均は0に近く、標準偏差は1に近くなります。正規化プロセスにより、トレーニングの安定性、速度、全体的なパフォーマンスが向上します。

コード

# xが入力である場合。(x - mean(x)) / sqrt(variance(x) + epsilon) * gamma + beta

まとめ：

この時点で、エンコーダーの主要な内部機能について理解を深めました。さらに、モデルの学習能力を向上させる、純粋に技術的で重要なテクニックであるスキップ接続も探求しました。

このセクションは少し複雑ですが、すでにトランスフォーマーのアーキテクチャ全体について相当な理解を得ています。シリーズを進めるにつれて、この理解は残りの部分を理解するのに役立つでしょう。この複雑な分野での最先端の技術です。簡単なことではありません。すべてを100%理解していなくても、これまでの進展におめでとうございます！

次の部分は、機械学習の基礎的な（かつより単純な）概念であるフィードフォワードニューラルネットワークについて説明します。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!