Cox回帰の隠されたダークシークレット：Coxを解きほぐす

Title Unveiling the Hidden Dark Secret of Cox Regression Deciphering Cox

完璧な予測子はなぜp値0.93になるのか？

完璧な予測子について深掘り

以前のブログ記事をフォローしてくださっている方は、ロジスティック回帰が完全に分離されたデータに遭遇した場合、無限のオッズ比を導く問題があることを思い出すかもしれません。オッズの代わりにハザードを使用する Cox 回帰では、完璧な予測子においても同様の問題が発生するかどうか疑問に思うかもしれません。発生しますが、ロジスティック回帰とは異なり、ここではどのように問題が発生するかがほとんど分かっておらず、何が「完璧な予測子」と見なされるかさえ明確ではありません。後でより明確になるように、完璧な予測子とは、イベント時間の順位と完全に一致する予測子xのことを指します（スピアマン相関は1である）。

以前、「Unbox the Cox」という記事で:

Cox回帰の直感的なガイド：Cox回帰を理解する

ハザードと最尤推定は、イベントランキングをどのように予測するのか？

towardsdatascience.com

最尤推定を説明し、寿命を延ばす薬の投与量を表す唯一の予測子xを持つ5人の対象者の作り話のデータセットを紹介しました。xをイベント時間の完璧な予測子にするために、ここでは対象者CとDのイベント時間を入れ替えました:

• Pythonを使用して北極の氷の傾向を分析する
• DataFrameを効率的に操作するためのloc Pandasメソッドの使い方
• Pandas 2.0 データサイエンティストにとってのゲームチェンジャー？

import numpy as npimport pandas as pdimport plotnine as p9from cox.plots import (    plot_subject_event_times,    animate_subject_event_times_and_mark_at_risk,    plot_cost_vs_beta,)perfect_df =  pd.DataFrame({    'subject': ['A', 'B', 'C', 'D', 'E'],    'time': [1, 3, 4, 5, 6],    'event': [1, 1, 1, 1, 0],    'x': [-1.7, -0.4, 0.0, 0.9, 1.2],})plot_subject_event_times(perfect_df, color_map='x')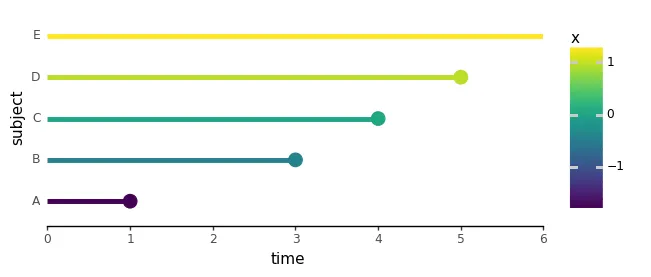

これらの「完璧な予測子」がなぜ問題になるのかを理解するために、ここで直前の続きからβに対して負の対数尤度コストをプロットしたものを確認してみましょう:

negloglik_sweep_betas_perfect_df = neg_log_likelihood_all_subjects_sweep_betas(    perfect_df,    betas=np.arange(-5, 5, 0.1))plot_cost_vs_beta(negloglik_sweep_betas_perfect_df, width=0.1)

すぐにわかるように、βの最小値はもはや存在しません。非常に大きな負のβ値を使用すると、すべてのイベントに対してほぼ完璧な対数尤度適合度が得られます。

そして、次にこの背後にある数学について掘り下げ、イベントAの尤度を見てみましょう。βを微調整していくと、分子と分母がどのように変化するかを調べていきます:

βが高い、つまり大きな正の数である場合、最後の項（xの最大値である1.2を持つ）が分母全体を支配し、極端に大きくなります。したがって、尤度は小さくなり、ゼロに近づきます:

これにより、大きな負の対数尤度が得られます。最後の被験者Eのハザードは常に分子内のどのハザードよりも大きくなるため、各個別の尤度でも同じことが起こります。その結果、AからDの被験者の負の対数尤度が増加します。この場合、βが高いと、すべての尤度が低下し、すべてのイベントの適合度が低下するため、不良な適合度が得られます。

今、βが低いか、大きな負の数値である場合、分母の最初の項は被験者Aのハザードを表しており、最も低いx値を持っているため、支配的になります。分子内にも同じ被験者Aのハザードが現れるため、βをますます負にすることで、尤度L（A）を任意の値に近づけ、ほぼ完全な適合度を作成できます。

すべての他の個別の尤度にも同じことが当てはまります。負のβは、すべてのイベントの尤度を同時に増加させます。基本的に、負のβを持つことにはデメリットはありません。同時に、個別のハザードが増加します（xが負であるAおよびBの被験者）、同じままです（x = 0のCの被験者）、または減少します（正のxのDの被験者）。ただし、ここで本当に重要なのは、ハザードの比率です。この手描きの数学をプロットして個別のハザードを確認できます。

def plot_likelihoods(df, ylim=[-20, 20]):    betas = np.arange(ylim[0], ylim[1], 0.5)    subjects = df.query("event == 1")['subject'].tolist()    likelihoods_per_subject = []    for subject in subjects:        likelihoods = [            np.exp(log_likelihood(df, subject, beta))            for beta in betas        ]        likelihoods_per_subject.append(            pd.DataFrame({                'beta': betas,                'likelihood': likelihoods,                'subject': [subject] * len(betas),            })                )    lik_df = pd.concat(likelihoods_per_subject)    return (        p9.ggplot(lik_df, p9.aes('beta', 'likelihood', color='subject'))        + p9.geom_line(size=2)        + p9.theme_classic()    )    plot_likelihoods(perfect_df)

ハザードの比率としてまとめられる尤度の方法は、負のβ値が予測子のランクよりも大きいイベント時刻のランクが同等またはそれ以上の各被験者の尤度に「完全な適合度」を提供することを意味します！副産物として、xがイベント時刻と完全に負のスピアマン相関を持つ場合、任意の正のβは任意の良好な適合度を与えます。

予測子と時間のランクが合わない場合

実際には、イベント時刻のランクと予測子のランクが一致しない場合、何が起こるか、別の架空の例を使用して示すことができます：

sample_df = pd.DataFrame({    'subject': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'],    'x': [-1.7, -0.4, 0.0, 0.5, 0.9, 1.2, 1.3, 1.45],    'time': [1, 2, 4, 3, 5, 7, 6, 8],    'rank_x': [1, 2, 3, 4, 5, 6, 7, 8],    'event': [1, 1, 1, 1, 1, 1, 1, 0],})sample_df

この特定の例では、time列は1から8までの範囲で、各値が独自のランクを表しています。また、予測子xのランクを示すx_rank列もあります。ここで、重要な観察点があります。被験者DとGのx_rankは、対応するtimeランクよりも実際に高いため、βが大きく負の値をとる場合には、DとGの尤度は分子と分母の間で相殺効果を経験しません。

現在、βの中間有限値で、尤度は最大になっています。個々の尤度のプロットを見てみましょう。

plot_likelihoods(sample_df)

時間と予測子の間のこれらの「不一致した」ランクは、有意に負のβがある場合に、すべての尤度が本質的に1つに折りたたまれるのを防ぐために重要な役割を果たします。

結論として、Cox回帰では、予測子xのランクがイベント時間のランクよりも低い場合に少なくとも1つのインスタンスが必要です。

完璧は善の敵である（p値）

では、これらの完璧な予測子は実際のシナリオでどのように振る舞うのでしょうか？調査するために、再びlifelinesライブラリに戻りましょう。

from lifelines import CoxPHFitterperfect_cox_model = CoxPHFitter()perfect_cox_model.fit(  perfect_df,  duration_col='time',  event_col='event',  formula='x')perfect_cox_model.print_summary()

#> /.../coxph_fitter.py:1586: ConvergenceWarning:#> The log-likelihood is getting suspiciously close to 0 and the delta is still large.#> There may be complete separation in the dataset.#> This may result in incorrect inference of coefficients.#> See https://stats.stackexchange.com/q/11109/11867 for more.#> /.../__init__.py:1165: ConvergenceWarning:#> Column x has high sample correlation with the duration column.#> This may harm convergence.#> This could be a form of 'complete separation'.#> See https://stats.stackexchange.com/questions/11109/how-to-deal-with-perfect-separation-in-logistic-regression#> /.../coxph_fitter.py:1611:#> ConvergenceWarning: Newton-Rhaphson failed to converge sufficiently.#> Please see the following tips in the lifelines documentation:#> https://lifelines.readthedocs.io/en/latest/Examples.html#problems-with-convergence-in-the-cox-proportional-hazard-model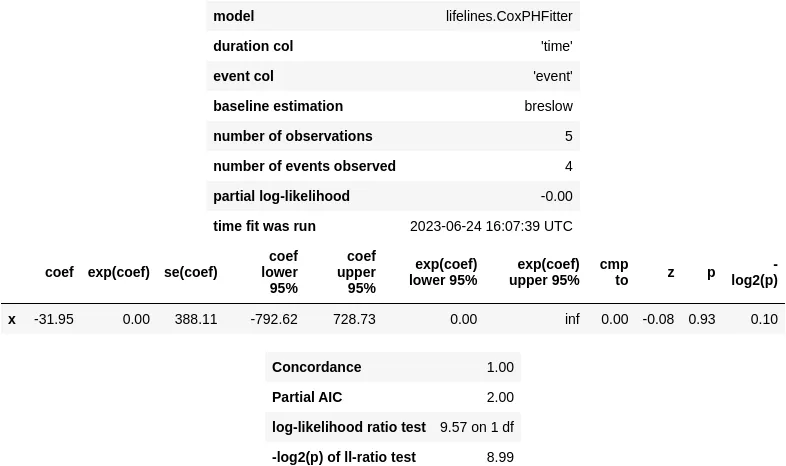

ロジスティック回帰と同様に、収束警告が発生し、予測子係数βの信頼区間が非常に広くなっています。その結果、p値は0.93になります。

この問題を考慮せずにp値に基づいてモデルを単にフィルタリングすると、これらの完璧な予測子を見落としてしまいます。

この収束問題に対処するために、lifelinesライブラリのドキュメントといくつかの役立つStackOverflowスレッドは、コスト関数に正則化項を組み込むことを提案しています。この項は、大きな係数値に対するコストを効果的に増加させ、penalizer引数をゼロより大きな値に設定することでL2正則化を活性化できます。

perfect_pen_cox_model = CoxPHFitter(penalizer=0.01, l1_ratio=0)perfect_pen_cox_model.fit(perfect_df, duration_col='time', event_col='event', formula='x')perfect_pen_cox_model.print_summary()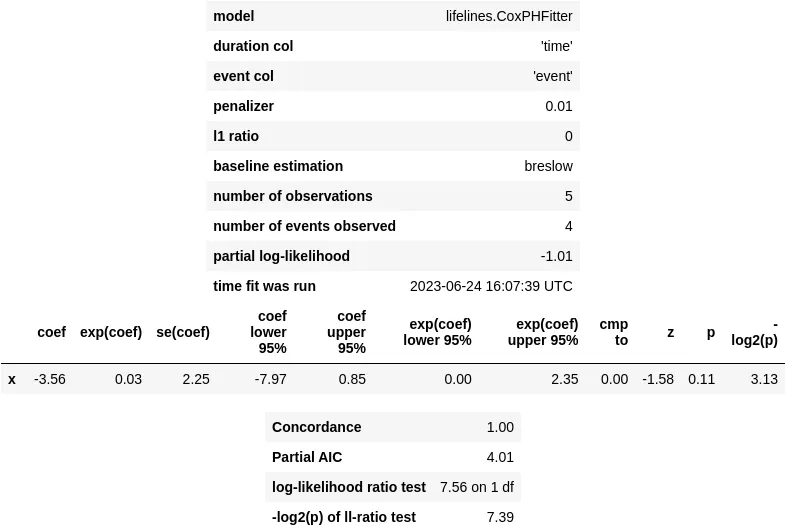

このアプローチは、収束警告を修正しますが、この厄介なp値を縮小するにはあまり効果がありません。この正則化トリックでも、完璧な予測子のp値は0.11というある程度大きな値になります。

時間は相対的であり、ランクだけが重要です

最後に、前回の例を使用して、イベント時刻の絶対値がCox回帰の適合性に影響を与えないことを検証します。これを行うには、time列と同じ順序でランダムな数字を含むtime2という新しい列を導入します。

sample_df = pd.DataFrame({    'subject': ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'],    'x': [-1.7, -0.4, 0.0, 0.5, 0.9, 1.2, 1.3, 1.45],    'time': [1, 2, 4, 3, 5, 7, 6, 8],    'rank_x': [1, 2, 3, 4, 5, 6, 7, 8],    'event': [1, 1, 1, 1, 1, 1, 1, 0],}).sort_values('time')np.random.seed(42)sample_df['time2'] = sorted(np.random.randint(low=-42, high=888, size=8))sample_df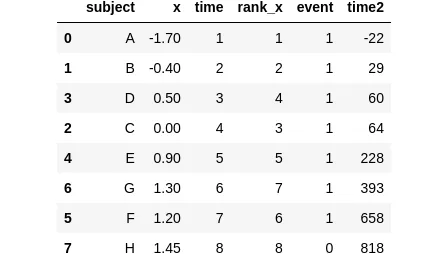

彼らの適合度は確かに同一です:

sample_cox_model = CoxPHFitter()sample_cox_model.fit(  sample_df,  duration_col='time',  event_col='event',  formula='x')sample_cox_model.print_summary()

sample_cox_model = CoxPHFitter()sample_cox_model.fit(  sample_df,  duration_col='time2',  event_col='event',  formula='x')sample_cox_model.print_summary()

結論

このようなことから何を学べたでしょうか？

• 生存モデルにおける完全予測変数とは、予測変数の順位がイベント時刻の順位と完全に一致するものです。
• Cox回帰は、有限の係数βでこれらの完全予測変数を適合させることができず、広い信頼区間と大きなp値を生じます。
• 実際のイベント時刻の値はあまり重要ではなく、その順位がすべてです。
• イベント時刻と予測変数の順位が一致しない場合、大きなβ値の尤度における便利なキャンセル効果を得ることができません。したがって、少なくとも一つの順位が一致しないケースが必要です。
• 一部のファンシーな正則化手法を試しても、実際の状況で完全予測変数は依然として厄介な広い信頼区間と高いp値を与える場合があります。
• ロジスティック回帰と同様に、p値に本当に興味がない場合、正則化手法を使用すると、予測が正しい便利なモデル適合を提供してくれます！

コードを自分で実行したい場合は、私のGithubからIPythonノートブックを使用してください: https://github.com/igor-sb/blog/blob/main/posts/cox_perfect.ipynb

次回の投稿までさようなら！ 👋

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!