「The Reformer – 言語モデリングの限界を押し上げる」
The Reformer - Pushing the limits of language modeling
Reformerが半ミリオントークンのシーケンスを訓練するために8GB未満のRAMを使用する方法
Reformerモデルは、Kitaev、Kaiserらによって2020年に紹介されたもので、現在のところ最もメモリ効率の良いトランスフォーマーモデルの1つです。
最近、長いシーケンスモデリングは大きな関心を集めており、今年だけでも多くの論文が提出されています(Beltagyら(2020年)、Royら(2020年)、Tayら、Wangらなど)。長いシーケンスモデリングの背後にある動機は、要約、質問応答などの多くのNLPタスクが、BERTなどのモデルよりも長い入力シーケンスを処理する必要があるということです。大きな入力シーケンスを処理する必要があるタスクでは、長いシーケンスモデルはメモリオーバーフローを避けるために入力シーケンスを切り詰める必要がなく、従って標準の「BERT」のようなモデルを上回る性能を示すことが示されています(Beltagyら(2020年)による)。
Reformerは、このデモに示されているように、一度に最大で半ミリオンのトークンを処理する能力により、長いシーケンスモデリングの限界を em em ます。比較のために、従来の bert-base-uncased モデルでは、入力の長さを512トークンに制限しています。Reformerでは、標準のトランスフォーマーアーキテクチャの各部分が最小限のメモリ要件を最適化するために再設計されており、性能の大幅な低下を伴わずにメモリの改善がなされています。
- より小さく、より速い言語モデルのためのブロック疎行列
- エンコーダー・デコーダーモデルのための事前学習済み言語モデルチェックポイントの活用
- 実践におけるFew-shot学習:GPT-Neoと🤗高速推論API
メモリの改善は、Reformerの作者がトランスフォーマーワールドに導入した4つの特徴に帰属できます:
- Reformer Self-Attention Layer – ローカルコンテキストに制限されることなく自己注意を効率的に実装する方法は?
- Chunked Feed Forward Layers – 大規模なフォワードレイヤーの時間とメモリのトレードオフを改善する方法は?
- Reversible Residual Layers – スマートな残差アーキテクチャにより、トレーニング時のメモリ消費を劇的に削減する方法は?
- Axial Positional Encodings – 非常に大きな入力シーケンスで位置エンコーディングを使用可能にする方法は?
このブログ記事の目的は、上記の4つのReformerの特徴について読者に詳細な理解を与えることです。説明はReformerに焦点を当てていますが、各特徴が他のトランスフォーマーモデルにとってどのような状況で効果的であるかについての直感をより良く得ることができるでしょう。4つのセクションは緩く関連しているため、個別に読むこともできます。
Reformerは🤗Transformersライブラリの一部です。Reformerのユーザーは、モデルの動作方法や正しい設定の方法をよりよく理解するために、この非常に詳細なブログ記事を読むことをお勧めします。すべての方程式には、Reformerの設定に対応する公式のドキュメントや設定ファイルにすぐに関連付けることができるように、それぞれの等価な名前が付けられています(例:config.<param_name>)。
注意:Axial Positional Encodingsは公式のReformer論文では説明されていませんが、公式のコードベースで広範に使用されています。このブログ記事はAxial Positional Encodingsの最初の詳細な説明を提供します。
1. Reformer自己注意層
Reformerは、2種類の特殊な自己注意層を使用します:ローカル自己注意層とLocality Sensitive Hashing(LSH)自己注意層です。
これらの新しい自己注意層をより良く紹介するために、まずはVaswaniら(2017年)で紹介された従来の自己注意であるグローバル自己注意を簡単に復習しましょう。
このブログ記事では、人気のあるブログ記事「The illustrated transformer」と同じ表記法と色付けを使用しているため、読者はまずこのブログ記事を読むことを強くお勧めします。
重要:Reformerは元々因果自己注意のために導入されましたが、双方向自己注意にも十分に使用することができます。この記事では、Reformerの自己注意は双方向自己注意のために紹介されています。
グローバル自己注意の復習
すべてのTransformerモデルの中心は自己注意層です。従来の自己注意層、ここではグローバル自己注意層と呼ぶことにします。埋め込みベクトルシーケンス X = x 1 , … , x n \mathbf{X} = \mathbf{x}_1, \ldots, \mathbf{x}_n X = x 1 , … , x n に対してトランスフォーマーレイヤーを適用すると仮定しましょう。ここで、各ベクトル x i \mathbf{x}_{i} x i はサイズ config.hidden_size、つまり d h d_h d h です。
簡単に言うと、グローバル自己注意層は、クエリ、キー、値行列 Q、K、V に X を射影し、次のようにソフトマックス演算を使用して出力 Z を計算します:Z = SelfAttn(X) = softmax(QKT)V(キーの正規化因子と自己注意の重み WO を省略しています)。完全なトランスフォーマ操作の詳細については、illustrated transformer を参照してください。
視覚的には、n = 16、d h = 3 の場合、この操作を次のように表すことができます:

すべての視覚化では、batch_size と config.num_attention_heads は 1 と想定されています。一部のベクトル、例えば x3 とその対応する出力ベクトル z3 は、後で LSH自己注意をよりよく説明するためにマークされています。提示されたロジックは、マルチヘッド自己注意(config.num_attention_heads > 1)にも簡単に拡張できます。マルチヘッド自己注意の参照として illustrated transformer を読むことをお勧めします。
重要なことは、各出力ベクトル zi に対して、全体の入力シーケンス X が処理されるということです。内積テンソル QKT のメモリの増加の複雑さは通常、トランスフォーマモデルのメモリボトルネックを表します(O(n^2) の記憶量のオーダー)。これが、bert-base-cased が config.max_position_embedding_size を 512 に制限している理由でもあります。
ローカル自己注意
ローカル自己注意は、O(n^2) のメモリボトルネックを減らすための明らかな解決策であり、計算コストを削減しながらより長いシーケンスをモデル化することができます。ローカル自己注意では、入力 X = X1:n = x1, …, xn を n_c 個のチャンクに分割します:X = [X1:lc, …, X((nc – 1) * lc : nc * lc)] 各チャンクの長さは config.local_chunk_length、つまり lc です。その後、各チャンクごとにグローバル自己注意が適用されます。
視覚化のために、n = 16、d h = 3 の入力シーケンスを再表示します:
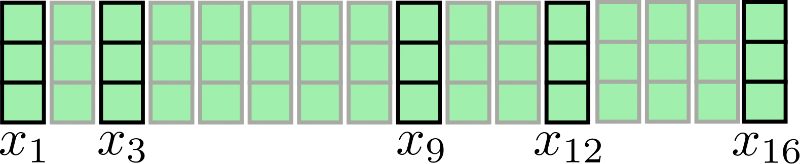
仮に lc = 4, nc = 4 とすると、チャンク付きのアテンションは以下のように表されます:

上記のように、アテンション演算は各チャンク X1:4, X5:8, X9:12, X13:16 に個別に適用されます。このアーキテクチャの最初の欠点は明らかです:一部の入力ベクトルは直近のコンテキストにアクセスできません。例えば、x9 は x8 にアクセスできず、逆もまた同様です。これは、これらのトークンが直近のコンテキストを考慮に入れた単語表現を学習することができないため問題です。
簡単な修正方法は、各チャンクに config.local_num_chunks_before(np)と config.local_num_chunks_after(na)を追加することです。つまり、各入力ベクトルが少なくとも np 個の前の入力ベクトルと na 個の後続の入力ベクトルにアクセスできるようにします。これは、オーバーラップを持つチャンク分割とも理解できます。np と na は各チャンクが前のすべてのチャンクおよび後続のチャンクとどれだけオーバーラップするかを定義します。この拡張されたローカルセルフアテンションを以下のように示します:
Zloc = [ Z1:lcloc, … , Z(nc – 1) * lc : nc * lcloc ]
ただし、Zlc * (i – 1) + 1 : lc * i loc = SelfAttn( Xlc * (i – 1 – np) + 1 : lc * (i + na) )[ np * lc : -na * lc ]、∀i ∈ { 1, … , nc }
上記の式はかなり複雑に見えます。Reformerのセルフアテンション層では通常、na は 0 に設定され、np は 1 に設定されます。したがって、i = 1 の場合の式を再度書き直します:
Z1:lcloc = SelfAttn( X-lc + 1 : lc )[ lc : ]
私たちは、最初のセグメントが最後のセグメントにも参加できるという循環関係があることに気付きました。これを少し改良されたローカルアテンションで説明しましょう。まず、各ウィンドウセグメント内でセルフアテンションを適用し、中央の出力セグメントのみを保持します。
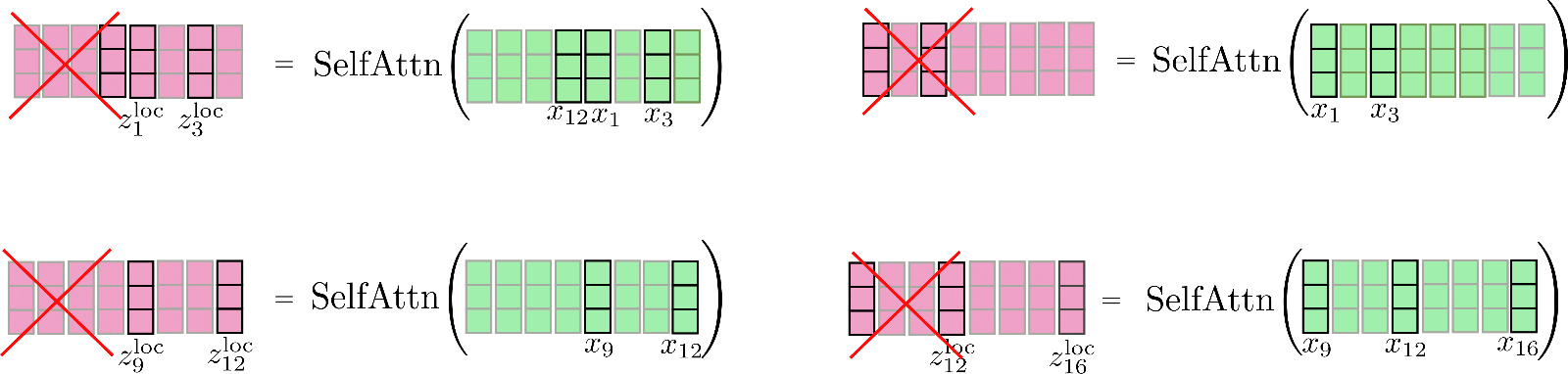
最後に、関連する出力は Z loc \mathbf{Z}^{\text{loc}} Z loc に連結され、次のようになります。
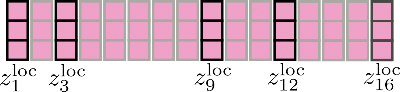
ローカルセルフアテンションは効率的な方法で実装されているため、赤いクロスで示されているように、出力が計算されてから「捨てられる」ことはありません(イラストのために表示しています)。
ここで重要なのは、チャンク化されたセルフアテンション関数の各入力ベクトルを拡張することで、このセルフアテンション関数の各単一の出力ベクトル z i \mathbf{z}_{i} z i がより良いベクトル表現を学習できることです。たとえば、各出力ベクトル z 5 loc , z 6 loc , z 7 loc , z 8 loc \mathbf{z}_{5}^{\text{loc}}, \mathbf{z}_{6}^{\text{loc}}, \mathbf{z}_{7}^{\text{loc}}, \mathbf{z}_{8}^{\text{loc}} z 5 loc , z 6 loc , z 7 loc , z 8 loc は、すべての入力ベクトル X 1 : 8 \mathbf{X}_{1:8} X 1 : 8 を考慮してより良い表現を学習できます。
メモリ消費の利点は明らかです。O ( n 2 ) \mathcal{O}(n^2) O ( n 2 ) のメモリの複雑さは、それぞれのセグメントごとに分割されるため、総合的な漸近メモリ消費量は O ( n c ∗ l c 2 ) = O ( n ∗ l c ) \mathcal{O}(n_{c} * l_{c}^2) = \mathcal{O}(n * l_{c}) O ( n c ∗ l c 2 ) = O ( n ∗ l c ) に減少します。
この改良されたローカルセルフアテンションは、バニラのローカルセルフアテンションアーキテクチャよりも優れていますが、まだ大きな欠点があります。すなわち、各入力ベクトルは事前に定義されたサイズのローカルコンテキストにのみ参照できるということです。入力ベクトル間の長距離の依存関係を学習する必要のないNLPタスク(たとえば音声認識、固有表現認識、短い文の因果言語モデリングなど)では、これは大きな問題ではないかもしれません。しかし、多くのNLPタスクでは、モデルに長距離の依存関係を学習する必要があり、ローカルセルフアテンションは性能の低下につながる可能性があります。
- 質問応答:モデルは質問トークンと関連する回答トークンの関係を学習する必要がありますが、これらはおそらく同じローカル範囲にはないでしょう
- 多肢選択:モデルは通常、有意な長さで分割された複数の回答トークンセグメントを比較する必要があります
- 要約:モデルはコンテキストトークンの長いシーケンスと要約トークンの短いシーケンスの関係を学習する必要がありますが、ローカルセルフアテンションでは関連する関係を捉えることはできないでしょう
- など…
ローカルセルフアテンションだけでは、トランスフォーマーモデルが入力ベクトル(トークン)間の関連関係を学習するのに十分ではない可能性があります。
そのため、Reformerでは、グローバルセルフアテンションを近似する効率的なセルフアテンション層であるLSHセルフアテンションを追加で使用しています。
LSHセルフアテンション
さて、ローカルセルフアテンションの仕組みがわかったので、Reformerのおそらく最も革新的な部分に取り組むことができます:ローカリティセンシティブハッシング(LSH)セルフアテンション。
LSHセルフアテンションの前提は、ローカルセルフアテンションとほぼ同じくらい効率的でありながら、グローバルセルフアテンションを近似することです。
LSHセルフアテンションは、Andoni et al(2015)で紹介されたLSHアルゴリズムに基づいています。
LSHセルフアテンションのアイデアは、もし n n n が大きい場合、Q K T \mathbf{Q}\mathbf{K}^T Q K T のアテンションドット積の重みに対してソフトマックスが適用されると、各クエリベクトルに対して値の大きな値ベクトルがほんのわずかしか存在しないという洞察に基づいています。
さらに詳しく説明しましょう。k i ∈ K = [ k 1 , … , k n ] T、q i ∈ Q = [ q 1 , … , q n ] Tをキーベクトルとクエリベクトルとします。q i について、計算 softmax ( q i T K T ) は、q i と cosine 類似度が高い k j のキーベクトルのみを使用して近似することができます。これは、softmax 関数が入力値が大きいほど指数関数的に重みを増やすためです。これまでのところ順調ですが、次の問題は、すべての i について q i と cosine 類似度が高いベクトルを効率的に見つけることです。
まず、Reformer の著者は、クエリとキープロジェクションを共有することが性能に影響しないことに気付いています。つまり、Q = K です。これにより、各クエリベクトル q i について cosine 類似度が高いキーベクトルを見つける必要がなくなります。代わりに、クエリベクトル同士の cosine 類似度を見つける必要があります。これは重要です。なぜなら、クエリ-クエリベクトルの内積近似には推移的な性質があるからです。つまり、q i がクエリベクトル q j と q k と cosine 類似度が高い場合、q j も q k と cosine 類似度が高いことになります。したがって、クエリベクトルはバケットにクラスタリングされます。同じバケットに属するすべてのクエリベクトルは互いに cosine 類似度が高いです。C m を m 番目の位置インデックスのセットとしましょう。このセットには、対応するクエリベクトルが同じバケットに属しています。また、config.num_buckets、つまり n b をバケットの数とします。
インデックスセット C m に対して、softmax 関数は対応するバケットのクエリベクトル softmax ( Q i ∈ C m Q i ∈ C m T ) の softmax 関数をグローバルな self-attention と共有クエリとキープロジェクションの softmax ( q i T Q T ) の近似としています。すべての位置インデックス i について C m 内の近似された softmax 関数が適用されます。
次に、著者は LSH(Locality Sensitive Hashing)アルゴリズムを使用してクエリベクトルを事前定義されたバケット数 n b にクラスタリングしています。LSH アルゴリズムは非常に効率的であり、cosine 類似度の最近傍アルゴリズムの近似です。このノートブックでは LSH スキームの説明は範囲外なので、ただそのことを覚えておきましょう。各ベクトル q i は、LSH アルゴリズムによって n b 個の事前定義されたバケットのうちの1つに位置インデックス i を割り当てられます。つまり、LSH ( q i ) = m、ただし i ∈ { 1 , … , n }、m ∈ { 1 , … , n b } です。
視覚的には、元の例に対して次のように示すことができます:

第3に、n b つのバケットにクエリベクトルをクラスタ化した場合、対応するインデックスの集合 C m は、入力ベクトル x 1 、…、x n を順番に並べ替えるために使用できます。2 {}^2 2 したがって、共有のクエリキーの自己注意を局所的な注意のように部分的に適用することができます。
例として、入力ベクトル X = x 1 、…、x 16 、config.num_buckets = 4、config.lsh_chunk_length = 4 と仮定しましょう。上のグラフを見ると、各クエリベクトル q 1 、…、q 16 は、クラスタ C 1 、C 2 、C 3 、C 4 のいずれかに割り当てられていることがわかります。対応する入力ベクトル x 1 、…、x 16 をそれに応じて並べ替えると、次のような並べ替えられた入力 X ′ が得られます。
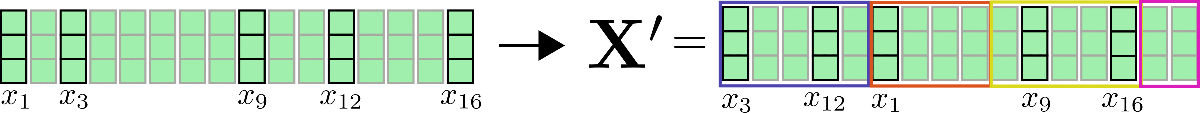
自己注意機構は、各クラスタごとに適用する必要があります。したがって、各クラスタ C m に対応する出力は次のように計算されます: Z i ∈ C m LSH = SelfAttn Q = K ( X i ∈ C m )。
例をもう一度説明しましょう。
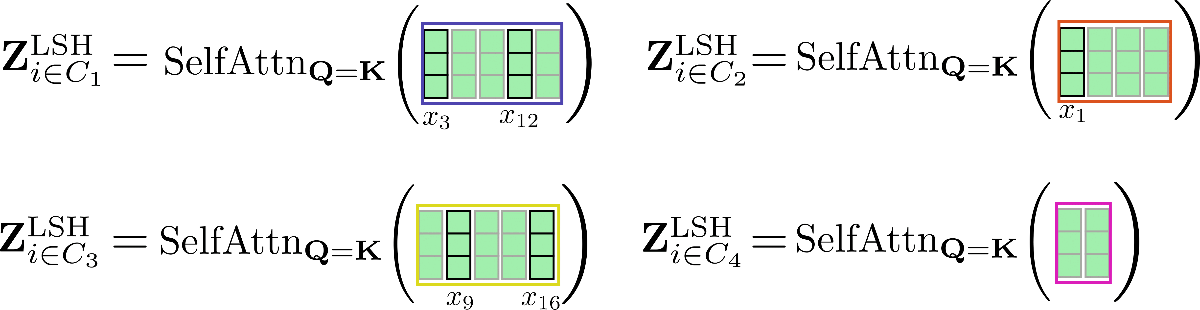
上記のように、自己注意機能は異なるサイズの行列に対して動作するため、GPUやTPUでの効率的なバッチ処理には適していません。
この問題を解決するために、並べ替えられた入力をローカル注意と同様にconfig.lsh_chunk_lengthのサイズのチャンクに分割することができます。並べ替えられた入力をチャンクに分割することで、バケットは2つの異なるチャンクに分割される可能性があります。この問題を解決するために、LSH自己注意では、各チャンクが自身に加えて前のチャンクconfig.lsh_num_chunks_before = 1にアテンドするようになっています(通常、config.lsh_num_chunks_afterは0に設定されます)。この方法で、バケット内のすべてのベクトルが高い確率でお互いにアテンドすることが保証されます。
すべてのチャンク k ∈ { 1 , … , n c } に対して、LSH自己注意は次のように記述できます:
Z ′ l c ∗ k + 1:l c ∗ ( k + 1 ) LSH = SelfAttn Q = K ( X ′ l c ∗ k + 1:l c ∗ ( k + 1 ) ) [ l c : ]。
X ′ と Z ′ は、LSHアルゴリズムに従って入力ベクトルと出力ベクトルを並び替えたものです。複雑な数式は十分です。では、LSHセルフアテンションを説明しましょう。
上記のように並び替えられたベクトル X ′ は、チャンクに分割され、共有クエリキーセルフアテンションが各チャンクに適用されます。
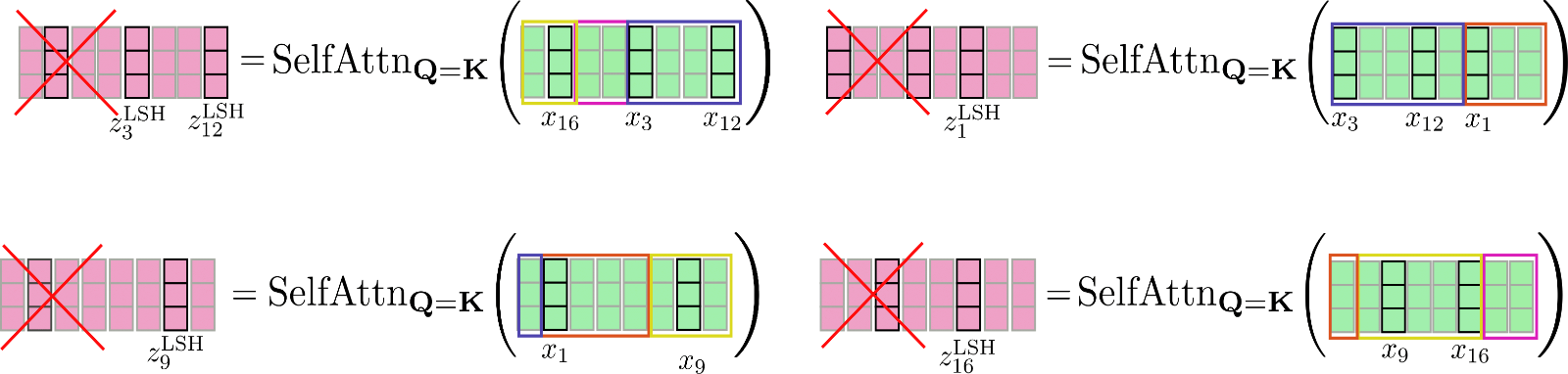
最後に、出力 Z ′ LSH が元の並び順に並べ替えられます。
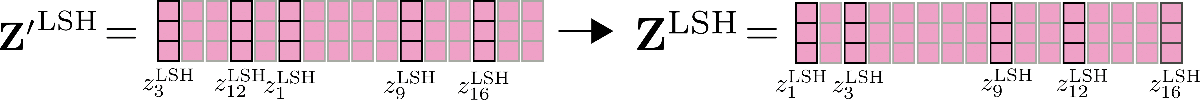
また、LSHセルフアテンションの精度は、異なるランダムなLSHハッシュを使用して、並列に LSHセルフアテンション config.num_hashes 回実行することで改善することができます。 config.num_hashes > 1 を設定することで、各出力位置 i ごとに複数の出力ベクトル z i LSH , 1 , … , z i LSH , n h を計算し、結合します。具体的には、 z i LSH = ∑ k n h Z i LSH , k ∗ weight i k です。 weight i k は、その他のハッシュラウンドと比較してハッシュラウンド k の出力ベクトル z i LSH , k の重要性を表し、ソフトマックス計算の正規化項に指数的に比例します。これは、対応するクエリベクトル q i k が対応するチャンク内の他のクエリベクトルとの余弦類似度が高い場合、このチャンクのソフトマックス正規化項は高くなり、対応する出力ベクトル q i k はグローバルアテンションに対するより良い近似値となり、重みが付けられます。詳細については、論文の付録Aを参照してください。この例では、マルチラウンドLSHセルフアテンションは次のように表現できます。
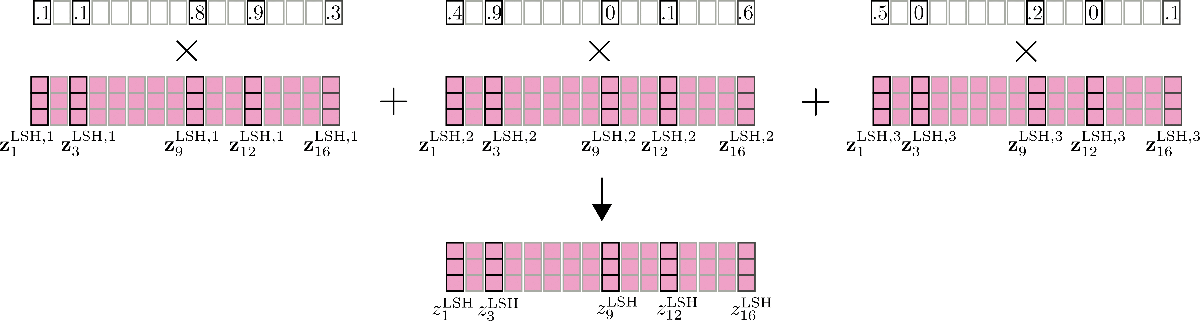
素晴らしいです。これで、ReformerにおけるLSHセルフアテンションの動作原理がわかりました。
メモリの複雑さに関しては、メモリボトルネックと競合する2つの項目があります:ドット積:O(nh * nc * lc^2) = O(n * nh * lc) と LSHバケッティングに必要なメモリ:O(n * nh * nb^2) です。ただし、ここで lc はチャンクの長さを表します。大きな n の場合、バケットの数 n b^2 がチャンクの長さ lc よりもはるかに高速に増加するため、ユーザーは再びバケットの数 config.num_buckets をここで説明されているように因数分解することができます。
まず、前述した内容を簡単に振り返りましょう:
- 私たちは、softmax演算が非常に少数のキーベクトルに重みを付けることを知っているため、グローバルな注意を近似したいと考えています。
- キーベクトルがクエリベクトルと等しい場合、つまり、各クエリベクトルq i \mathbf{q}_{i} q i に対して、softmaxはコサイン類似性の観点で類似している他のクエリベクトルにのみ重みを付けます。
- この関係は双方向で機能し、q j \mathbf{q}_{j} q j がq i \mathbf{q}_{i} q i に類似している場合、q j \mathbf{q}_{j} q j はq i \mathbf{q}_{i} q i にも類似しているため、順列入力に自己注意を適用する前にグローバルクラスタリングを行うことができます。
- 順列入力に対してローカル自己注意を適用し、出力を元の順列に並べ替えます。
1 {}^{1} 1 著者は、共有クエリキーセルフアテンションが標準的なセルフアテンションとほぼ同じくらいの性能を発揮することを示す予備的な実験を行いました。
2 {}^{2} 2 より正確には、バケット内のクエリベクトルは元の順序に従ってソートされます。つまり、例えばベクトルq 1 、q 3 、q 7 \mathbf{q}_1, \mathbf{q}_3, \mathbf{q}_7 q 1 , q 3 , q 7 がすべてバケット2にハッシュされた場合、バケット2内のベクトルの順序はq 1 \mathbf{q}_1 q 1 が続き、q 3 \mathbf{q}_3 q 3 、q 7 \mathbf{q}_7 q 7 です。
3 {}^3 3 余談ですが、クエリベクトルq i \mathbf{q}_{i} q i にはマスクがかけられており、自己アテンションの対象から除外されます。ベクトルとその他のベクトルとのコサイン類似性と比較して、ベクトルとそれ自体のコサイン類似性は常に高いかそれ以上になるため、共有クエリキーセルフアテンションのクエリベクトルは、自分自身に注意を向けることが強く排除されます。
ベンチマーク
ベンチマークツールは最近Transformersに追加されました-詳細な説明はこちらをご覧ください。
“local” + “LSH”セルフアテンションを使用した場合にどれだけメモリを節約できるかを示すために、Reformerモデルgoogle/reformer-enwik8を、異なるlocal_attn_chunk_lengthとlsh_attn_chunk_lengthでベンチマークします。 google/reformer-enwik8モデルのデフォルトの構成と使用方法については、こちらで詳細を確認できます。
まず、必要なインポートとインストールを行いましょう。
#@title インストールとインポート
# pip インストール
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArgumentsまず、グローバルセルフアテンションを使用した場合のReformerモデルのメモリ使用量をベンチマークします。これは、lsh_attn_chunk_length = local_attn_chunk_length = 8192と設定することで、8192以下のすべての入力シーケンスに対して、モデルが自動的にグローバルセルフアテンションに切り替わるようにすることで実現できます。
config = ReformerConfig.from_pretrained("google/reformer-enwik8", lsh_attn_chunk_length=16386, local_attn_chunk_length=16386, lsh_num_chunks_before=0, local_num_chunks_before=0)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16386], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
result = benchmark.run()
HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1279.0, style=ProgressStyle(description…
1 / 1
GPUに収まりません。CUDAのメモリが不足しています。2.00 GiBを割り当てようとしました(GPU 0; 合計容量11.17 GiB; 既に割り当てられているのは8.87 GiBです; 空き容量1.92 GiB; PyTorchによって合計で8.88 GiBのメモリが予約されています)。
==================== 推論 - メモリ - 結果 ====================
--------------------------------------------------------------------------------
モデル名 バッチサイズ シーケンス長 メモリ(MB)
--------------------------------------------------------------------------------
Reformer 1 2048 1465
Reformer 1 4096 2757
Reformer 1 8192 7893
Reformer 1 16386 N/A
--------------------------------------------------------------------------------入力シーケンスが長いほど、入力シーケンスとピークメモリ使用量の間には、二次関数の関係 O(n^2) がより明確に現れます。実際には、入力シーケンスを倍にするとピークメモリ使用量が4倍になることを明確に観察するには、はるかに長い入力シーケンスが必要です。
これにより、グローバルアテンションを使用した google/reformer-enwik8 モデルでは、16K以上のシーケンス長ではメモリオーバーフローが発生します。
では、モデルのデフォルトパラメータを使用して、ローカルおよびLSHセルフアテンションを有効にしましょう。
config = ReformerConfig.from_pretrained("google/reformer-enwik8")
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[2048, 4096, 8192, 16384, 32768, 65436], batch_sizes=[1], models=["Reformer"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config], args=benchmark_args)
result = benchmark.run()
1 / 1
GPUに収まりません。CUDAのメモリが不足しています。2.00 GiB (GPU 0; 11.17 GiBの総容量; 7.85 GiBがすでに割り当てられています; 1.74 GiBが利用可能; PyTorchにより合計9.06 GiBが予約されています) を割り当てようとしました。
GPUに収まりません。CUDAのメモリが不足しています。4.00 GiB (GPU 0; 11.17 GiBの総容量; 6.56 GiBがすでに割り当てられています; 3.99 GiBが利用可能; PyTorchにより合計6.81 GiBが予約されています)
==================== 推論 - メモリ - 結果 ====================
--------------------------------------------------------------------------------
モデル名 バッチサイズ シーケンス長 メモリ(MB)
--------------------------------------------------------------------------------
Reformer 1 2048 1785
Reformer 1 4096 2621
Reformer 1 8192 4281
Reformer 1 16384 7607
Reformer 1 32768 N/A
Reformer 1 65436 N/A
--------------------------------------------------------------------------------予想通り、ローカルおよびLSHセルフアテンションを使用すると、より長い入力シーケンスに対してメモリ効率が向上し、このノートブックの11GB RAM GPUでは16Kトークンまでしかメモリが足りません。
2. チャンク化されたフィードフォワードレイヤー
Transformerベースのモデルでは、通常、セルフアテンションレイヤーの後に非常に大きなフィードフォワードレイヤーが並列して使用されます。そのため、このレイヤーは全体のメモリのかなりの部分を占め、時にはモデルのメモリのボトルネックとなることさえあります。Reformerの論文で最初に紹介されたフィードフォワードのチャンキングは、メモリの消費を改善するために時間の消費を増やす効果的な技術です。
Reformerのチャンク化されたフィードフォワードレイヤー
Reformerでは、LSH(またはローカルセルフアテンション)レイヤーの後に通常、リジュアル接続が続き、これがトランスフォーマーブロックの最初の部分を定義します。詳細については、このブログを参照してください。
トランスフォーマーブロックの最初の部分である規格化されたセルフアテンションの出力は、Z ‾ = Z + X と書くことができます。ここで、Z はReformerの Z LSH または Z loc です。
例として、入力 x 1 、…、x 16 に対する規格化されたセルフアテンションの出力を以下に示します。

次に、トランスフォーマーブロックの2番目の部分は、通常、2つのフィードフォワードレイヤーからなります。1つは Z に対して Linear int ( … ) を適用し、中間出力 Y int を生成し、もう1つは中間出力を処理して出力 Y out を生成します。2つのフィードフォワードレイヤーは次のように定義できます。
Y out = Linear out ( Y int ) = Linear out ( Linear int ( Z ‾ ) ) .
この時点で、フィードフォワード層の出力である位置 y out, i の数学的には、この位置の入力 y ‾ i にのみ依存することを覚えておくことが重要です。セルフアテンション層とは異なり、すべての出力 y out, i は、異なる位置のすべての入力 y ‾ j ≠ i に対して完全に独立しています。
z ‾ 1 から z ‾ 16 までのフィードフォワード層を図で示しましょう。
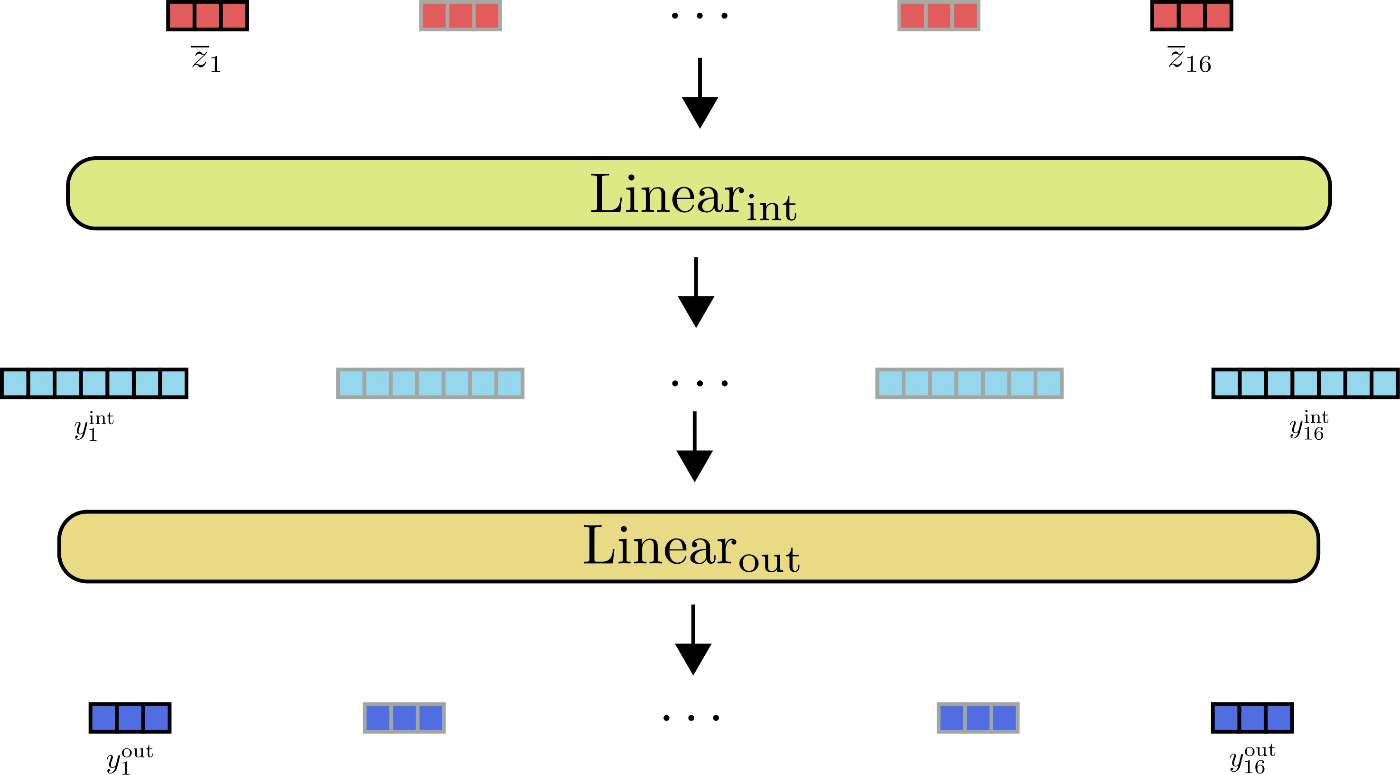
図からわかるように、すべての入力ベクトル z ‾ i は、同じフィードフォワード層で並列に処理されます。
フィードフォワード層の出力次元に注目すると興味深くなります。Reformerでは、Linear int の出力次元は config.feed_forward_size、つまり d f であり、Linear out の出力次元は config.hidden_size、つまり d h です。
Reformerの著者は、transformerモデルでは、中間次元 d f が出力次元 2 d h よりもはるかに大きい傾向にあることを観察しました。つまり、次元 d f × n のテンソル Y int は、総メモリのかなりの部分を割り当て、さらにはメモリのボトルネックになる可能性があります。
次元の違いをより感じるために、例の行列 Y int と Y out を描画しましょう。
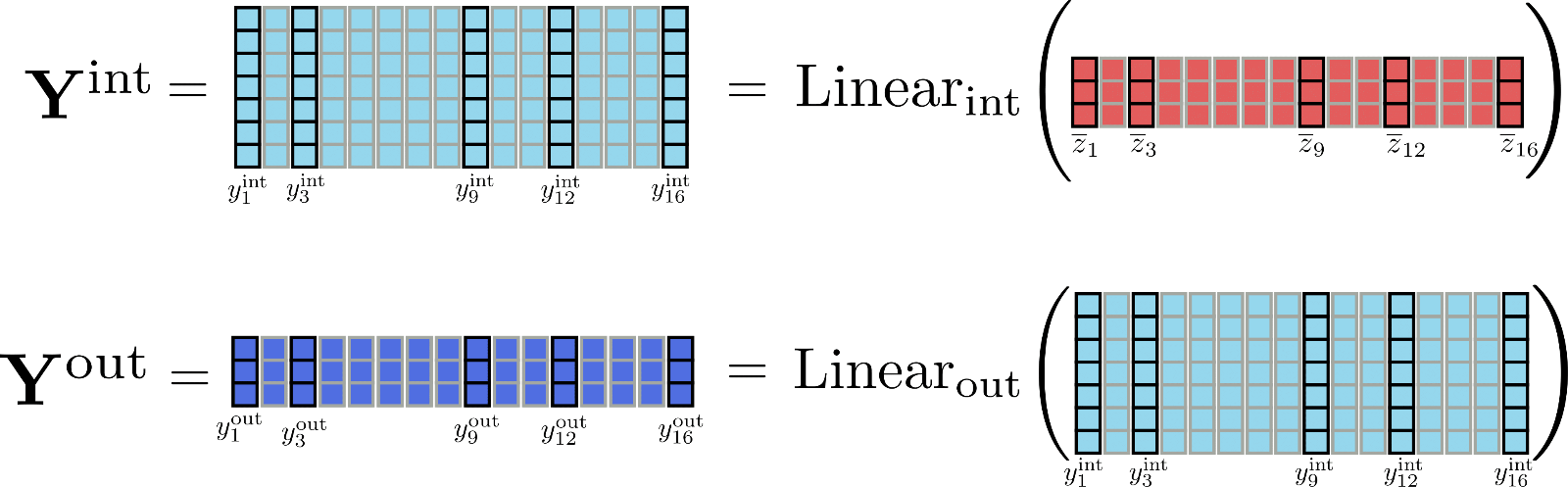
明らかに、テンソル Y int は Y out よりもはるかに多くのメモリ(具体的には d f d h × n 倍)を保持しています。しかし、完全な中間行列 Y int を計算する必要は本当にありますか?実際には必要ありません。メモリの代わりに速度を重視するため、リニア層の計算を一度に1つのチャンクだけ処理することができます。config.chunk_size_feed_forwardを c f と定義し、チャンク化されたリニア層は次のように定義されます:Y out = [Y out, 1:c f, …, Y out, (n – c f):n]。ここで、Y out, (c f * i):(i * c f + i) = Linear out (Linear int (Z ‾ (c f * i):(i * c f + i)))です。実際には、出力は段階的に計算され、結果は一時的なテンソル Y int をメモリに保存することなく連結されます。
この例では、c f = 1 c_{f}=1 c f = 1 と仮定して、位置 i = 9 i=9 i = 9 の出力の増分計算を以下のように示すことができます。
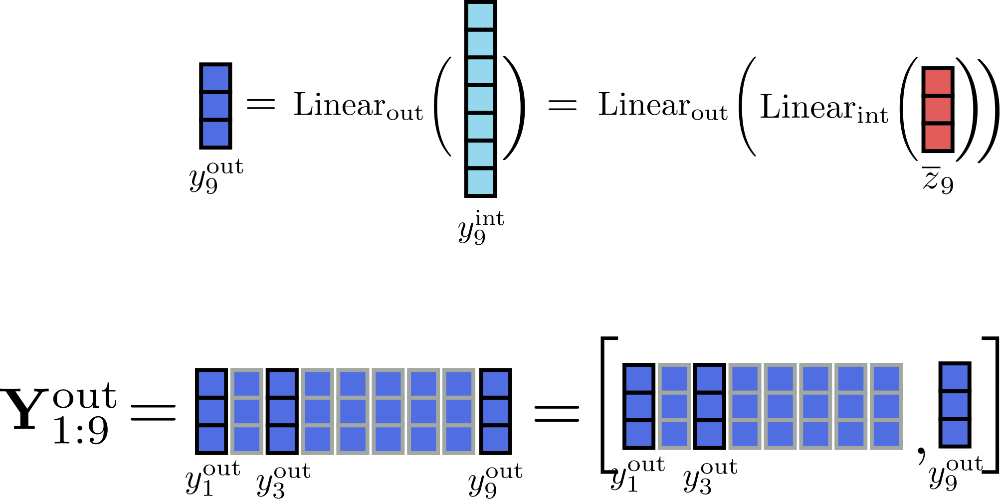
サイズ 1 のチャンクで入力を処理することにより、同時にメモリに保存する必要があるテンソルは、最大サイズ 16 × d h 16 \times d_{h} 1 6 × d h の Y out \mathbf{Y}_\text{out} Y out 、サイズ d f d_{f} d f の y int , i \mathbf{y}_{\text{int}, i} y int , i 、およびサイズ 16 × d h 16 \times d_{h} 1 6 × d h の入力 Z ‾ \mathbf{\overline{Z}} Z だけです。ここで、d h d_{h} d h は config.hidden_size 3 ^{3} 3 です。
最後に、チャンクされた線形層は数学的に等価な出力を生成するため、すべてのトランスフォーマーの線形層に適用できます。したがって、config.chunk_size_feed_forward を使用することで、特定のユースケースにおいてメモリと速度のトレードオフを改善することができます。
1 {}^1 1 より簡単な説明のため、通常は Z ‾ \mathbf{\overline{Z}} Z がフィードフォワード層によって処理される前に適用されるレイヤーノームレイヤーは現在省略されています。
2 {}^2 2 例えば、bert-base-uncased では、中間次元 d f d_{f} d f は出力次元 d h d_{h} d h よりも 3072 倍大きいです。
3 {}^3 3 明示性とこのノートブックでの説明のために、出力 config.num_attention_heads は 1 であると仮定し、自己注意層の出力はサイズ config.hidden_size であると仮定します。
チャンクされた線形/フィードフォワード層に関する詳細は、🤗Transformers ドキュメントのこちらをご覧ください。
ベンチマーク
チャンクされたフィードフォワード層を使用することで、どれだけのメモリが節約されるかをテストしてみましょう。
#@title インストールとインポート
# pip インストール
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments
Building wheel for transformers (setup.py) ... [?25l[?25hdoneまず、デフォルトの google/reformer-enwik8 モデルとチャンクされたフィードフォワード層を使用したモデルを比較してみましょう。
config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8") # チャンクなし
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1) # フィードフォワードチャンク
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()
1 / 2
GPU に収まりません。CUDA メモリ不足です。2.00 GiB の割り当てを試行しました (GPU 0; 総容量 11.17 GiB; 7.85 GiB が既に割り当てられています; 1.74 GiB の空きがあります; PyTorch によって合計 9.06 GiB が予約されています)
2 / 2
GPU に収まりません。CUDA メモリ不足です。2.00 GiB の割り当てを試行しました (GPU 0; 総容量 11.17 GiB; 7.85 GiB が既に割り当てられています; 1.24 GiB の空きがあります; PyTorch によって合計 9.56 GiB が予約されています)
==================== 推論 - メモリ - 結果 ====================
--------------------------------------------------------------------------------
モデル名 バッチサイズ シーケンス長 メモリ(MB)
--------------------------------------------------------------------------------
Reformer-No-Chunk 8 1024 4281
Reformer-No-Chunk 8 2048 7607
Reformer-No-Chunk 8 4096 N/A
Reformer-Chunk 8 1024 4309
Reformer-Chunk 8 2048 7669
Reformer-Chunk 8 4096 N/A
--------------------------------------------------------------------------------興味深いことに、チャンクされたフィードフォワードレイヤーは全く役に立ちません。その理由は、config.feed_forward_sizeが十分に大きくないため、実際の差が生じないからです。シーケンスの長さが4096以上の場合にのみ、わずかなメモリ使用量の減少が見られます。
フィードフォワードレイヤーのサイズを4倍に増やし、注意ヘッドの数も4分の1に減らして、フィードフォワードレイヤーがメモリボトルネックとなるようにして、メモリピーク使用量がどのように変化するか見てみましょう。
config_no_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=0, num_attention_{h}eads=2, feed_forward_size=16384) # no chuck
config_chunk = ReformerConfig.from_pretrained("google/reformer-enwik8", chunk_size_feed_forward=1, num_attention_{h}eads=2, feed_forward_size=16384) # feed forward chunk
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[1024, 2048, 4096], batch_sizes=[8], models=["Reformer-No-Chunk", "Reformer-Chunk"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_chunk, config_chunk], args=benchmark_args)
result = benchmark.run()
1 / 2
2 / 2
==================== 推論 - メモリ - 結果 ====================
--------------------------------------------------------------------------------
モデル名 バッチサイズ シーケンス長 メモリ(MB)
--------------------------------------------------------------------------------
Reformer-No-Chunk 8 1024 3743
Reformer-No-Chunk 8 2048 5539
Reformer-No-Chunk 8 4096 9087
Reformer-Chunk 8 1024 2973
Reformer-Chunk 8 2048 3999
Reformer-Chunk 8 4096 6011
--------------------------------------------------------------------------------長い入力シーケンスではピークメモリ使用量が明確に減少しています。結論として、チャンクされたフィードフォワードレイヤーは、注意ヘッドが少なくフィードフォワードレイヤーが大きいモデルにのみ意味があります。
3. 可逆残差レイヤー
可逆残差レイヤーは、最初にN. Gomezらによって紹介され、人気のあるResNetモデルのトレーニング時のメモリ消費量を削減するために使用されました。数学的には、可逆残差レイヤーは「本物の」残差レイヤーとは少し異なりますが、順伝播中にアクティベーションの保存を必要としないため、トレーニング時のメモリ消費量を劇的に削減することができます。
Reformerにおける可逆残差レイヤー
まず、モデルのトレーニングには推論よりもはるかに多くのメモリが必要な理由について調査してみましょう。
モデルを推論で実行する場合、必要なメモリはモデル内で計算される最大のテンソルのメモリとほぼ同じです。一方、モデルをトレーニングする場合、必要なメモリは異なる可能性のあるすべての微分可能なテンソルの合計とほぼ同じです。
これは、ディープラーニングフレームワークで自動微分がどのように機能するかを考えれば驚くべきことではありません。トロント大学のRoger Grosseによるこの講義資料は、自動微分をよりよく理解するために役立ちます。
要するに、微分可能な関数(たとえば、レイヤー)の勾配を計算するためには、関数の出力と入力、および出力テンソルの勾配が必要です。勾配は動的に計算され、その後破棄されますが、関数の入力と出力テンソル(アクティベーションとも呼ばれます)は順伝播中に保存されます。
さて、これをトランスフォーマーモデルに適用してみましょう。トランスフォーマーモデルには、複数のトランスフォーマーレイヤーと呼ばれるスタックが含まれています。追加のトランスフォーマーレイヤーごとに、モデルは順伝播中により多くのアクティベーションを保存し、トレーニングに必要なメモリを増やします。詳細に見てみましょう。トランスフォーマーレイヤーは基本的に2つの残差レイヤーで構成されています。最初の残差レイヤーは、セルフアテンションメカニズムを表し、2)節で説明したように線形またはフィードフォワードレイヤーを表します。
前と同じ表記法を使用して、トランスフォーマーレイヤーの入力、すなわち X \mathbf{X} X は最初に正規化され、次にセルフアテンションレイヤーで処理されて出力 Z = SelfAttn ( LayerNorm ( X ) ) \mathbf{Z} = \text{SelfAttn}(\text{LayerNorm}(\mathbf{X})) Z = SelfAttn ( LayerNorm ( X ) ) を得ます。これらの2つのレイヤーを G G G と略記し、Z = G ( X ) \mathbf{Z} = G(\mathbf{X}) Z = G ( X ) とします。次に、残差 Z \mathbf{Z} Z を入力 Z ‾ = Z + X \mathbf{\overline{Z}} = \mathbf{Z} + \mathbf{X} Z = Z + X に追加し、その合計を第2の残差レイヤーである2つの線形レイヤーに供給します。Z ‾ \mathbf{\overline{Z}} Z は2番目の正規化レイヤーで処理され、その後2つの線形レイヤーで処理されて Y = Linear ( LayerNorm ( Z + X ) ) \mathbf{Y} = \text{Linear}(\text{LayerNorm}(\mathbf{Z} + \mathbf{X})) Y = Linear ( LayerNorm ( Z + X ) ) を得ます。2番目の正規化レイヤーと2つの線形レイヤーを F F F と略記し、Y = F ( Z ‾ ) \mathbf{Y} = F(\mathbf{\overline{Z}}) Y = F ( Z ) とします。最後に、残差 Y \mathbf{Y} Y を Z ‾ \mathbf{\overline{Z}} Z に追加して、トランスフォーマーレイヤーの出力 Y ‾ = Y + Z ‾ \mathbf{\overline{Y}} = \mathbf{Y} + \mathbf{\overline{Z}} Y = Y + Z とします。
完全なトランスフォーマーレイヤーを例として、x1、…、x16の例を使って説明しましょう。
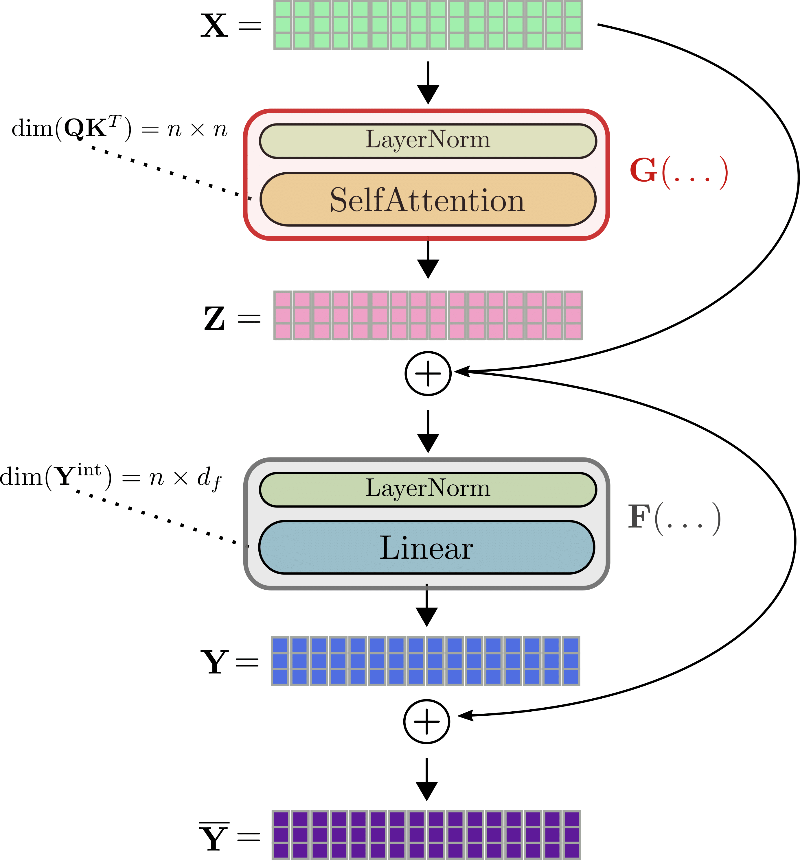
例えば、自己注意ブロックGの勾配を計算するためには、3つのテンソルが事前に知られている必要があります:勾配∂Z、出力Z、入力X。勾配∂Zはオンザフライで計算して後で破棄することができますが、ZとXの値はフォワードパス中に計算して保存する必要があります。なぜなら、バックプロパゲーション中に簡単にオンザフライで再計算することはできないからです。そのため、フォワードパス中には、大きなテンソル出力(例えば、クエリキーのドット積行列QKTや線形層の中間出力Yintなど)をメモリ2^2に保存する必要があります。
ここで、可逆残差層が役立ちます。アイデアは比較的シンプルです。残差ブロックは、関数の入力と出力テンソルを保存する必要がなく、バックワードパス中に両方を簡単に再計算できるように設計されています。そのため、フォワードパス中にはテンソルをメモリに保存する必要はありません。これは、2つの入力ストリームX(1)、X(2)と2つの出力ストリームY̅(1)、Y̅(2)を使用して達成されます。最初の残差Zは、最初の出力ストリームZ = G(X(1))によって計算され、その後、2番目の入力ストリームに追加されます。したがって、Z̅ = Z + X(2)です。同様に、残差Y = F(Z̅)は再び最初の入力ストリームに追加されます。したがって、2つの出力ストリームはY(1) = Y + X(1)およびY(2) = X(2) + Z = Z̅で定義されます。
可逆トランスフォーマーレイヤーは、x1、…、x16の場合には次のように可視化できます。
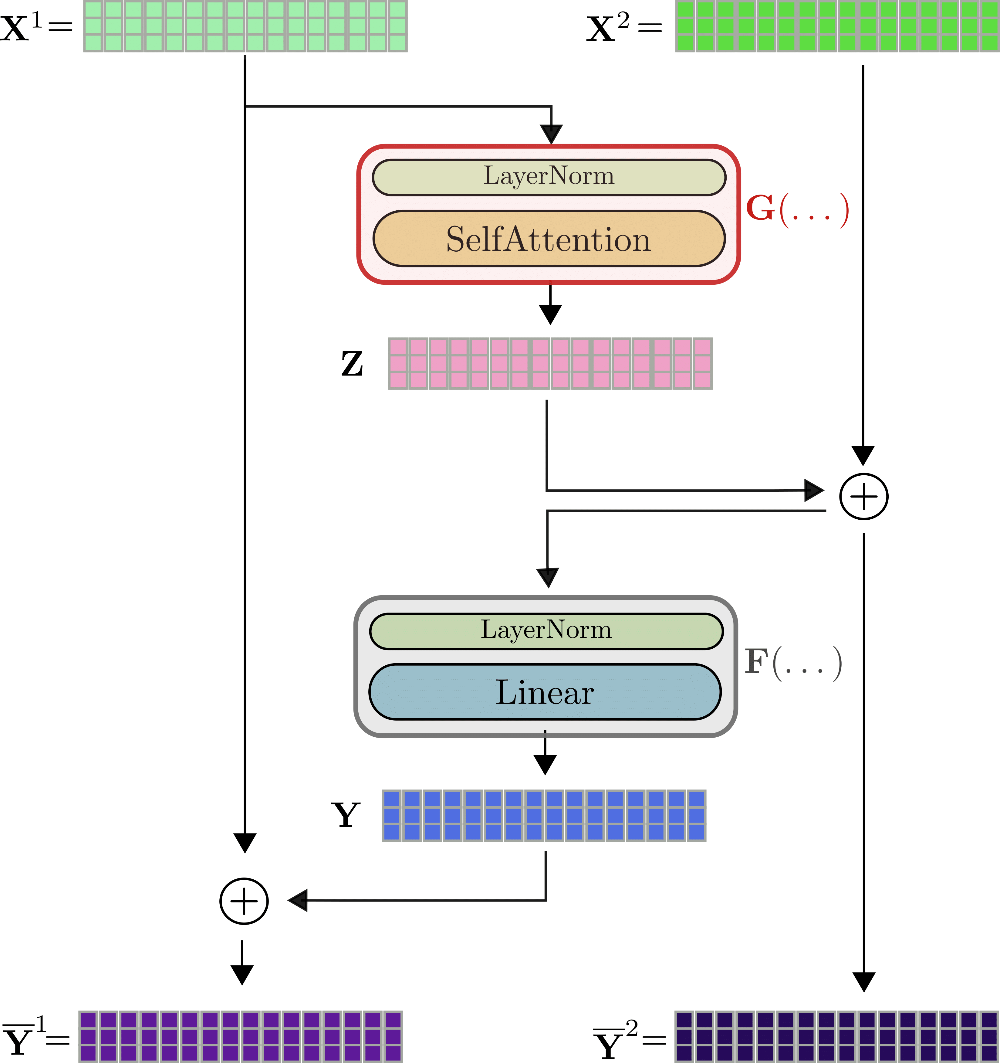
わかるように、出力Y̅(1)、Y̅(2)は非可逆レイヤーの出力Y̅と非常に似た方法で計算されますが、数学的には異なります。Reformerの著者は初期の実験で、可逆トランスフォーマーモデルのパフォーマンスが標準のトランスフォーマーモデルのパフォーマンスと一致することを観察しています。標準トランスフォーマーレイヤーとの最初の目に見える違いは、2つの入力ストリームと出力ストリームが存在することです。これにより、フォワードパスの必要なメモリがわずかに増加します。しかし、2つのストリームのアーキテクチャは、フォワードパス中にアクティベーションを保存する必要がないため、非常に重要です。説明しましょう。可逆トランスフォーマーレイヤーでは、バックプロパゲーションのために、勾配∂G、∂Fを計算する必要があります。オンザフライで計算できる勾配∂Y、∂Zに加えて、∂Fのためにテンソル値Y、Z̅、∂Gのためにテンソル値Z、X(1)が必要です。
Y ‾ ( 1 ) , Y ‾ ( 2 ) を知っていると仮定すると、グラフから以下のように X ( 1 ) , X ( 2 ) を計算することができます。X ( 1 ) = F ( Y ‾ ( 1 ) ) − Y ‾ ( 1 ) 、X ( 1 ) = F ( Y ( 1 ) ) − Y ( 1 ) 。さて、X ( 1 ) がわかったので、X ( 2 ) は X ( 2 ) = Y ‾ ( 1 ) − G ( X ( 1 ) ) として計算できます。そして、Y と Z は Y = Y ‾ ( 1 ) − X ( 1 ) 、Z = Y ‾ ( 2 ) − X ( 2 ) として簡単に計算できます。したがって、前向きパス中に最後の可逆トランスフォーマーレイヤーの出力 Y ‾ ( 1 ) , Y ‾ ( 2 ) のみを保存する場合、逆伝播中に G と F を使用して他の関連するアクティベーションを導出し、X ( 1 ) と X ( 2 ) を渡すことで計算できます。バックプロパゲーション中の各可逆トランスフォーマーレイヤーに対して G と F の2つの前向きパスのオーバーヘッドがありますが、前向きパス中のアクティベーションを保存する必要はありません。悪くない取引です!
注:最近、主要なディープラーニングフレームワークでは、逆伝播中に特定のアクティベーションのみを保存し、より大きなアクティベーションを再計算することができるコードがリリースされています(こちらのTensorflowとこちらのPyTorch)。標準の可逆レイヤーの場合、少なくとも1つのアクティベーションを各トランスフォーマーレイヤーごとに保存する必要がありますが、どのアクティベーションを動的に再計算できるかを定義することで、多くのメモリを節約することができます。
1 ^{1} 1 以前の2つのセクションでは、自己注意層と線形層の前にあるレイヤーノーム層を省略しました。読者は、自己注意と線形層に供給される前に、X と Z ‾ は両方ともレイヤーノーマリゼーションで処理されることを知っておくべきです。2 ^{2} 2 デザインでは、Q K の次元は n × n と書かれていますが、LSH自己注意層やローカル自己注意層では、次元はそれぞれ n × l c × n h または n × l c となります。ここで、l c はチャンクの長さ、n h はハッシュの数です。3 ^{3} 3 最初の可逆トランスフォーマーレイヤーでは、X ( 2 ) は X ( 1 ) に等しく設定されます。
ベンチマーク
可逆な残余レイヤーの効果を測定するために、BERTとReformerのメモリ使用量を、レイヤー数が増加するごとに比較します。
#@title インストールとインポート
# パッケージのインストール
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, BertConfig, PyTorchBenchmark, PyTorchBenchmarkArguments標準のbert-base-uncased BERTモデルの必要なメモリを、レイヤー数を4から12まで増やすことで測定しましょう。
config_4_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=4)
config_8_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=8)
config_12_layers_bert = BertConfig.from_pretrained("bert-base-uncased", num_hidden_layers=12)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Bert-4-Layers", "Bert-8-Layers", "Bert-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_bert, config_8_layers_bert, config_12_layers_bert], args=benchmark_args)
result = benchmark.run()
HBox(children=(FloatProgress(value=0.0, description='Downloading', max=433.0, style=ProgressStyle(description_…
1 / 3
2 / 3
3 / 3
==================== TRAIN - MEMORY - RESULTS ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Bert-4-Layers 8 512 4103
Bert-8-Layers 8 512 5759
Bert-12-Layers 8 512 7415
--------------------------------------------------------------------------------1つのBERTレイヤーを追加すると、必要なメモリが400MB以上線形的に増加することが分かります。
config_4_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=4, num_hashes=1)
config_8_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=8, num_hashes=1)
config_12_layers_reformer = ReformerConfig.from_pretrained("google/reformer-enwik8", num_hidden_layers=12, num_hashes=1)
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-4-Layers", "Reformer-8-Layers", "Reformer-12-Layers"], training=True, no_inference=True, no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_4_layers_reformer, config_8_layers_reformer, config_12_layers_reformer], args=benchmark_args)
result = benchmark.run()
1 / 3
2 / 3
3 / 3
==================== TRAIN - MEMORY - RESULTS ====================
--------------------------------------------------------------------------------
Model Name Batch Size Seq Length Memory in MB
--------------------------------------------------------------------------------
Reformer-4-Layers 8 512 4607
Reformer-8-Layers 8 512 4987
Reformer-12-Layers 8 512 5367
--------------------------------------------------------------------------------一方、Reformerでは、レイヤーを追加すると実際にはメモリの増加が少なくなります。1つのレイヤーを追加すると、平均して必要なメモリは100MB以下増加するため、より大きな12レイヤーのreformer-enwik8モデルは、12レイヤーのbert-base-uncasedモデルよりも少ないメモリを必要とします。
4. 軸方向の位置エンコーディング
Reformerは、巨大な入力シーケンスを処理することができます。ただし、そのような長い入力シーケンスの標準的な位置エンコーディングの重み行列だけでも、重みを保存するために1GB以上のメモリを使用します。そのような大きな位置エンコーディング行列を防ぐために、公式のReformerコードではAxial Position Encodingsが導入されました。
重要: Axial Position Encodingsは公式の論文では説明されていませんが、コードを見ることや著者との話し合いから理解することができます。
Reformerにおける軸方向位置符号化
Transformerは、自己注意層が順序の概念を持たないため、単語の順序を考慮するために位置符号化が必要です。位置符号化は通常、単純なルックアップ行列 E = [ e 1 , … , e n max ] \mathbf{E} = \left[\mathbf{e}_1, \ldots, \mathbf{e}_{n_\text{max}}\right] E = [ e 1 , … , e n max ] によって定義されます。位置符号化ベクトル e i \mathbf{e}_{i} e i は、単に i 番目の入力ベクトル x i + e i \mathbf{x}_{i} + \mathbf{e}_{i} x i + e i に加えられるため、モデルは入力ベクトル(トークンとも呼ばれる)が位置 i i i または位置 j j j にあるかどうかを区別することができます。各入力位置について、モデルは対応する位置符号化ベクトルをルックアップできる必要があります。そのため、E \mathbf{E} E の次元は、モデルが処理できる入力ベクトルの最大長 config.max_position_embeddings 、つまり n max n_\text{max} n max と入力ベクトルの次元 config.hidden_size 、つまり d h d_{h} d h によって定義されます。
d h = 4 d_{h}=4 d h = 4 および n max = 49 n_\text{max}=49 n max = 4 9 を仮定すると、このような位置符号化行列は次のように視覚化されます:

ここでは、次元(高さ)が 4 である位置符号化 e 1 \mathbf{e}_{1} e 1 、 e 2 \mathbf{e}_{2} e 2 、および e 49 \mathbf{e}_{49} e 4 9 のみを紹介しています。
0.5M トークンのシーケンスと入力ベクトル config.hidden_size = 1024 (ノートブックはこちら)で Reformer モデルをトレーニングしたいとします。対応する位置埋め込みは、パラメータ数が 0.5 M × 1024 ∼ 512 M 0.5M \times 1024 \sim 512M 0 . 5 M × 1 0 2 4 ∼ 5 1 2 M であり、これは 2GB のサイズに相当します。
このような位置符号化は、モデルをメモリに読み込むときやハードドライブにモデルを保存するときに、不必要に大量のメモリを使用します。
Reformerの著者は、config.hidden_size の次元を半分に減らし、n max n_\text{max} n max の次元をスマートに因数分解することで、位置符号化のサイズを劇的に縮小することに成功しました。Transformerでは、ユーザーは config.axial_pos_shape を適切な2つの値 n max 1 n_\text{max}^1 n max 1 および n max 2 n_\text{max}^2 n max 2 のリストに設定することで、n max n_\text{max} n max をどのように因数分解するかを決定できます。また、config.axial_pos_embds_dim を適切な2つの値 d h 1 d_{h}^{1} d h 1 および d h 2 d_{h}^2 d h 2 のリストに設定することで、隠れ層の次元をどのように切り分けるかを決定できます。さあ、もっと直感的に視覚化して説明しましょう。
n max n_{\text{max}} n max を因数分解することは、次元を第3軸に折りたたむことと考えることができます。以下に、因数分解 config.axial_pos_shape = [7, 7] の場合の例を示します:
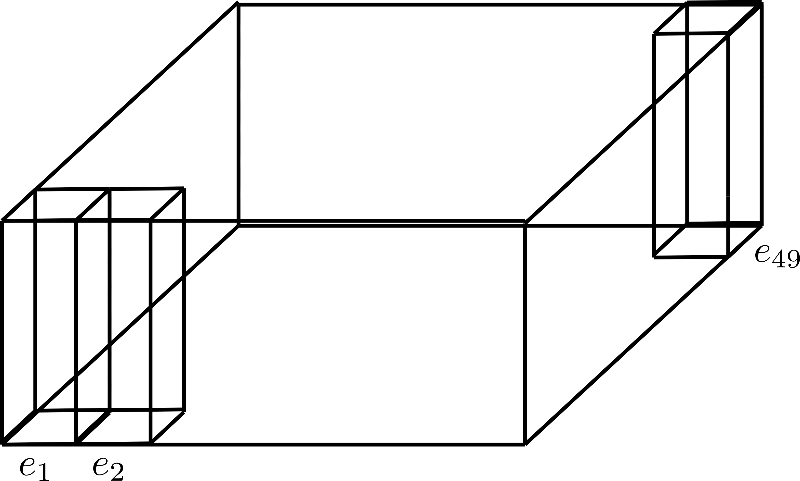
3つの立方体は、それぞれ符号化ベクトルe1、e2、e49に対応していますが、49個の符号化ベクトルは7つの行に分割されています。このアイデアは、7つの符号化ベクトルからなる1つの行のみを使用し、その値を他の6つの行に展開することです。異なる符号化ベクトルに同じ値を持つことは推奨されていないため、次元(高さ)がconfig.hidden_size=4の各ベクトルは、サイズ1の下位符号化ベクトルe downと、サイズ3の上位符号化ベクトルe upに分割されます。したがって、下部は行方向に、上部は列方向に展開されます。より明確にするために、視覚化してみましょう。
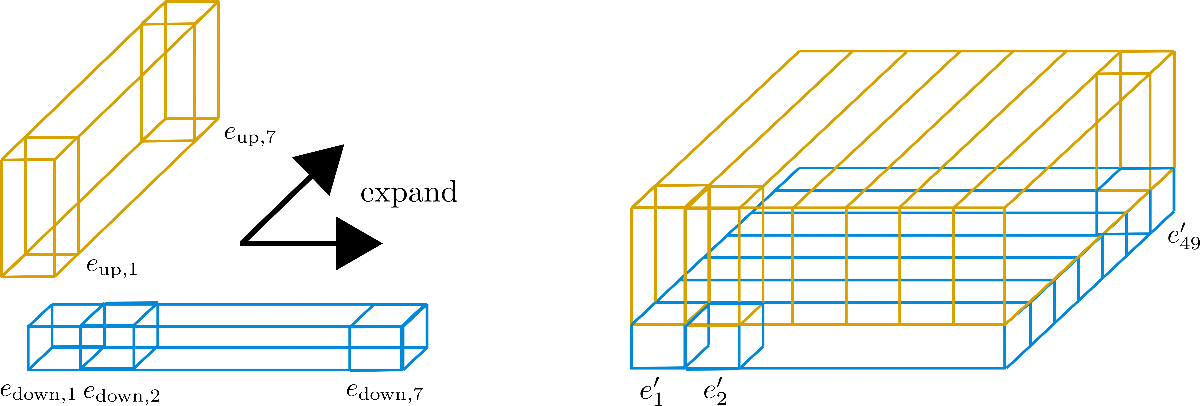
埋め込みベクトルは、e down(青色)とe up(黄色)に分割されていることがわかります。そして「サブ」ベクトルE down = [e down, 1, …, e down, 49]は、グラフィックの幅である7つの列のみを保持し、行方向に展開されます。逆に、「サブ」ベクトルE up = [e up, 1, …, e up, 49]は、7つの列のみを保持し、列方向に展開されます。その結果得られる埋め込みベクトルe’ iは以下のようになります。
e’ i = [[e down, i % n max 1] T, [e up, ⌊i/n max 2⌋] T] T
ここで、n max 1 = 7 および n max 2 = 7 です。これらの新しい符号化E’ = [e’ 1, …, e’ n max]は軸位置符号化と呼ばれます。
以下では、これらの軸位置エンコーディングが、例を通じてより詳細に説明されます。
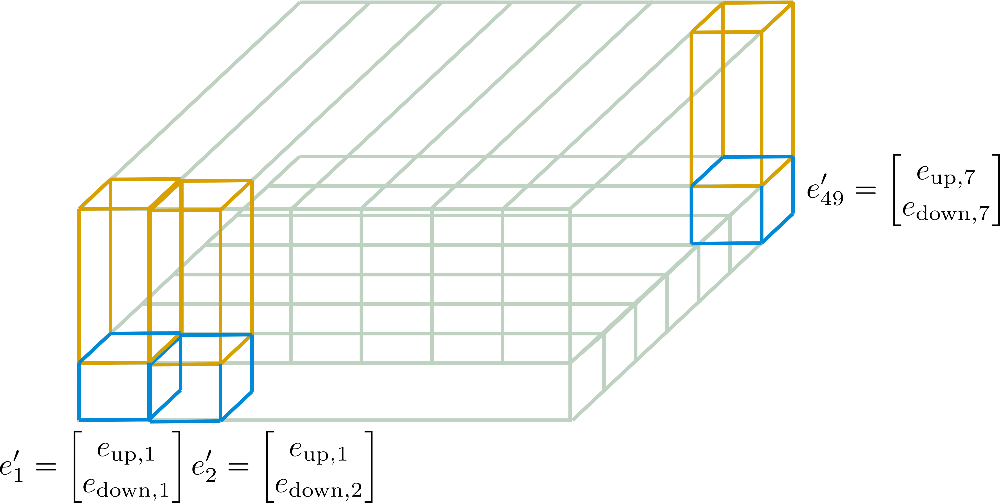
これにより、最終的な位置エンコーディングベクトルE’は、次元d_h1 × n_max1のE_down、および次元d_h2 × n_max2のE_upのみから計算されることがより理解しやすくなります。
ここで重要な点は、軸位置エンコーディングが、デザインによって各ベクトル[ e’1、…、e’n_max ]が互いに等しくないこと、およびエンコーディング行列の全体的なサイズが、n_max × d_hからn_max1 × d_h1 + n_max2 × d_h2に削減されることを確認することです。各軸位置エンコーディングベクトルがデザインによって異なるものになることを許すことで、軸位置エンコーディングがモデルによって学習される場合、効率的な位置表現を学習するための柔軟性が向上します。
サイズの劇的な削減を示すために、Reformerモデルに対してconfig.axial_pos_shape = [1024, 512]およびconfig.axial_pos_embds_dim = [512, 512]を設定したと仮定してみましょう。結果として得られる軸位置エンコーディング行列のサイズは、1024 × 512 + 512 × 512 ≈ 800Kパラメーターとなります。これは、この場合に標準の位置エンコーディング行列が必要とする2GBからの劇的な削減です。
より簡潔で数学的な説明については、🤗Transformersのドキュメントを参照してください。
ベンチマーク
最後に、従来の位置エンコーディングと軸位置エンコーディングのピークメモリ消費量を比較してみましょう。
#@title インストールとインポート
# pipのインストール
!pip -qq install git+https://github.com/huggingface/transformers.git
!pip install -qq py3nvml
from transformers import ReformerConfig, PyTorchBenchmark, PyTorchBenchmarkArguments, ReformerModel位置エンコーディングは、2つの設定パラメータにのみ依存します:入力シーケンスの最大許容長config.max_position_embeddingsおよびconfig.hidden_size。軸位置エンコーディングを使用することの効果を確認するために、入力シーケンスの最大許容長を50万トークンまで押し上げるモデルであるgoogle/reformer-crime-and-punishmentを使用します。
まず、軸位置エンコーディングと標準の位置エンコーディングの形状、およびモデル内のパラメータの数を比較します。
config_no_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=False) # 軸位置エンコーディングを無効にする
config_pos_axial_embeds = ReformerConfig.from_pretrained("google/reformer-crime-and-punishment", axial_pos_embds=True, axial_pos_embds_dim=(64, 192), axial_pos_shape=(512, 1024)) # 軸位置エンコーディングを有効にする
print("デフォルトの位置エンコーディング")
print(20 * '-')
model = ReformerModel(config_no_pos_axial_embeds)
print(f"位置エンコーディングの形状:{model.embeddings.position_embeddings}")
print(f"モデルのパラメータ数:{model.num_parameters()}")
print(20 * '-' + '\n\n')
print("軸位置エンコーディング")
print(20 * '-')
model = ReformerModel(config_pos_axial_embeds)
print(f"位置エンコーディングの形状:{model.embeddings.position_embeddings}")
print(f"モデルのパラメータ数:{model.num_parameters()}")
print(20 * '-' + '\n\n')
HBox(children=(FloatProgress(value=0.0, description='Downloading', max=1151.0, style=ProgressStyle(description…
デフォルトの位置エンコーディング
--------------------
位置エンコーディングの形状:PositionEmbeddings(
(embedding): Embedding(524288, 256)
)
モデルのパラメータ数:136572416
--------------------
軸位置エンコーディング
--------------------
位置エンコーディングの形状:AxialPositionEmbeddings(
(weights): ParameterList(
(0): Parameter containing: [torch.FloatTensor of size 512x1x64]
(1): Parameter containing: [torch.FloatTensor of size 1x1024x192]
)
)
モデルのパラメータ数:2584064
--------------------理論を読んだ後、軸方向の位置符号化重みの形状は読者にとって驚きではないはずです。
結果に関しては、このような長い入力シーケンスを処理できるモデルでは、デフォルトの位置符号化を使用することは実用的ではありません。 google/reformer-crime-and-punishment の場合、標準の位置符号化だけでも100M以上のパラメータを含んでいます。軸方向の位置符号化では、この数をわずか200K以上に減らすことができます。
最後に、推論時の必要なメモリを比較しましょう。
benchmark_args = PyTorchBenchmarkArguments(sequence_lengths=[512], batch_sizes=[8], models=["Reformer-No-Axial-Pos-Embeddings", "Reformer-Axial-Pos-Embeddings"], no_speed=True, no_env_print=True)
benchmark = PyTorchBenchmark(configs=[config_no_pos_axial_embeds, config_pos_axial_embeds], args=benchmark_args)
result = benchmark.run()
1 / 2
2 / 2
==================== 推論 - メモリ - 結果 ====================
--------------------------------------------------------------------------------
モデル名 バッチサイズ シーケンス長 メモリ(MB)
--------------------------------------------------------------------------------
Reformer-No-Axial-Pos-Embeddin 8 512 959
Reformer-Axial-Pos-Embeddings 8 512 447
--------------------------------------------------------------------------------google/reformer-crime-and-punishment の場合、軸方向の位置埋め込みを使用することで、メモリ要件がおおよそ半分に減少します。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






