再抽出を用いた統計的実験
'Statistical Experiment using Re-sampling'.
ブートストラップと順列検定

はじめに
データを扱う多くの人々は、観察を行い、その観察が統計的に有意であるかどうかを疑問に思います。そして、統計的推論の形式的な訓練や過去の経験を持っていない限り、最初に思い浮かぶのは、テストを実施する方法についてアドバイスを提供できる統計学者を見つけること、または少なくともテストが正しく実行され、結果が有効であることを確認してもらうことです。
これには多くの理由があります。まず、必要なテストがすぐには明らかにならないことがよくあります。テスト原則の基礎となる式、式の使用方法、およびテストを実施できるかどうか(たとえば、データが正規性などの必要条件を満たしていない場合)がすぐにはわかりません。statsmodelsなど、多くの統計モデルの推定や統計的テストを行うための包括的なRおよびPythonパッケージがあります。
それでも、統計理論を十分に理解せずに、ユーザーガイドの例を再現することでパッケージを使用すると、経験豊富な統計学者によってアプローチが厳密に検証された際に厳しい批判を受けることを心配する人もいます。私自身、エンジニアからデータアナリストになった経験があります。学部および大学院の課程で統計の授業を受けましたが、エンジニアが生計を立てるためには通常は統計を広範に使用しません。エンジニアリング、コンピュータサイエンス、化学などの形式的な訓練を受けたデータアナリストやデータサイエンティストも同様だと思います。
私は、最近、シミュレーションが古典的な式ベースの統計的手法の代わりに簡単に使用できることに気づいたため、この記事を書くことにしました。多くの人々は、平均の不確実性を推定するためにブートストラップを即座に思い浮かべるでしょう。しかし、ブートストラップについてだけではありません。ランダムな順列テスト内での再サンプリングを使用することで、多くの統計的推論の問題に答えることができます。このようなテストは一般的に非常に難しいものではありません。これらは、連続またはバイナリデータに対して適用され、サンプルサイズに関係なく、データの分布についての仮定を行いません。この意味で、順列テストは非パラメトリックであり、唯一の要件は交換可能性、つまりある値の特定の並びの観測確率が並べ替えのどの順列に対しても同じであることです。これほど要求されることはありません。
計算リソースの利用できなかったことは、過去に式ベースの統計的推論テストの驚異的な進歩の1つの理由かもしれません。数十または数千のレコードを持つデータサンプルを何千回も再サンプリングすることは、かつては禁止されていましたが、今では禁止されていません。これは、古典的な統計的推論手法がもはや必要ではないことを意味するのでしょうか?もちろん、そうではありません。しかし、順列テストを実行し、結果が類似している場合に確認することは、安心感を与えてくれるかもしれません。また、パッケージに頼らずにゼロから統計的テストを実行できる能力は、自己決定感を与えてくれます。
順列テストはもちろん新しいものではありませんが、いくつかの例と対応するコードを提供することは良いアイデアだと思いました。これにより、データの専門家の恐怖が和らぎ、シミュレーションを使用した統計的推論が日常の実践により近づくかもしれません。この記事では、順列テストを使用して2つの質問に答えます。順列テストを使用できるシナリオは他にも多くありますし、より複雑な質問に対する順列テストの設計はすぐに明らかにならない場合もあります。この意味では、この記事は包括的ではありません。ただし、原則は同じです。基本を理解することで、他のより微妙なビジネスの質問に答えるための順列テストの設計方法についての信頼性のある情報源を参照することが容易になります。私の意図は、母集団分布のシミュレーションを中心において、理論的な抽選を使用して観察された効果が偶然に発生する確率を推定することです。これが仮説検定の目的です。
統計的推論は仮説から始まります。たとえば、新しい薬が従来の治療法に比べて特定の病気に対してより効果的であるという仮説があります。効果は、新しい薬と従来の治療法(対照群)を使用した場合に、特定の血液指標(連続変数)の減少を確認することによって測定することができます。または、新しい薬を使用した場合に病気が検出されない動物の数(離散変数)を数えることによって測定することもできます。このような2つのグループの比較、またはA/Bテストは、すべての古典的な統計の教科書やこのような人気のあるテックブログで詳しく議論されています。薬剤設計の例を使用して、新しい薬が従来の治療法に比べて効果的であるかどうかをテストします(A/Bテスト)。これを基に、実際には従来の治療法よりも1%効果的であると仮定した場合に、新しい薬がより効果的であると結論付けるためには、何匹の動物が必要かを推定します。これらの2つの質問は関連しているようには見えないかもしれませんが、関連しています。2つめの質問に答えるために、最初の質問のコードを再利用します。すべてのコードは私のブログリポジトリで見つけることができます。
コメントは歓迎ですが、建設的にお願いします。統計学者のつもりはなく、私の意図は他の人々が順列検定に関して同様の学習プロセスを経るのを助けることです。
A/Bテスト
最初の質問に戻りましょう。つまり、新しい薬が従来の治療よりも効果的かどうかです。実験を実施すると、病気の動物は治療内容によって2つのグループに割り当てられます。動物はランダムにグループに割り当てられるため、治療の効果における観察された差異は、薬の効果によるものであるか、または偶然によって強い免疫系を持つ動物が新薬グループに割り当てられた結果であるかのいずれかです。これらの2つの状況を解きほぐす必要があります。つまり、観察された利益がランダムな偶然によって説明可能かどうかを調べたいのです。
イメージを作るためにいくつかの架空の数値を考えましょう。
応答変数はバイナリであり、つまり、治療が成功したかどうかです。応答変数が連続的な場合(これは古典的な統計テストではない場合です!)、順列検定は同様の方法で機能しますが、上記の表にはカウントではなく平均値や標準偏差が含まれます。
順列検定では、同じサイズの治療グループを使用する必要はないため、意図的に異なるサイズの治療グループを使用しています。この架空のA/Bテストには多数の動物が関与しており、新薬が有望であるようです。新薬は従来の治療よりも1.5%効果的です。サンプルが大きいため、これは有意です。私たちはこれについて後ほど戻ってきます。人間として、有意なことを見逃すことがあります。これが、仮説検定を標準化することが非常に重要な理由です。
「無効仮説は何も起こっていないと考えてください。つまり、すべては偶然で説明できるということです。」
A/Bテストでは、何も特別なことが観察されていないという基本的な仮定を使用します。これは無効仮説としても知られています。テストを実施する人は通常、無効仮説が成立しないことを証明したいと考えています。つまり、発見が行われたということです。言い換えると、対立仮説が真であるとされます。これを証明する方法の1つは、ランダムな偶然が観察されたものと同様に極端な差をもたらす確率が非常に低いことを示すことです。私たちは既に順列検定との関連性を見始めています。
すべての治療を受けた動物が1つのグループ(2487 + 1785匹の動物)に集められ、その後、元の治療グループと同じサイズの2つのグループにランダムに再分割される手順を想像してみてください。各動物について、治療が成功したかどうかがわかっているため、各グループごとに治癒した動物の割合を計算することができます。観察されたデータを使用して、新薬が治癒動物の割合を80.34から81.79%に増加させたことがわかりました。つまり、約1.5%の増加です。もし2つのグループを何度も再サンプリングした場合、新薬が従来の治療よりも治癒動物の割合を高くすることがどれくらい頻繁に起こるのでしょうか?この「どれくらい頻繁に起こるか」が、統計的推論における普遍的なp値です。それが頻繁に起こる場合、つまり、p値が快適なしきい値(通常は5%)よりも大きい場合は、実験で観察されたことは偶然の結果であり、したがって無効仮説は棄却されません。それがまれに起こる場合、偶然だけでは観察された差異をもたらすことはできず、したがって無効仮説は棄却されます(そして、あなたのチームが新薬を発見した場合、パーティーを開くことができます!)。私たちが順列で行ったことは、実際には、2つの治療グループが等価であるという無効仮説をシミュレートしたことです。
無効仮説がどのように定式化されているかをもう一度考えてみてください。これが順列検定の実施方法を決定するためのものです。上記の例では、何度も偶然によって新薬がより効果的であると思い込ませられる可能性を見たいのです。つまり、対立仮説と相補的な無効仮説は、新薬がより効率的でないか、または従来の治療と同じくらい効率的であるということを述べています。これは単方向テスト(双方向テスト、または双方向テストとも呼ばれる2方向テストとは対照的です)。別の視点で考えてみてください。新薬がより効果的であると思い込むことを、ランダムな偶然によって騙されたくありません。逆方向で騙されることは問題ではありません、なぜなら私たちは従来の治療を置き換えるつもりはないからです。2方向テストはp値が高くなりますので、無効仮説を棄却する可能性がより高く、より保守的です。ただし、それが適切なテストでない場合は使用すべきではありません。
順列検定は、最も一般的な場合に次のように定式化することができます。Gᵢ、i=1,..,Nᴳのカーディナリティ ∣ Gᵢ ∣、i=1,..,Nᴳが存在すると仮定してください:
- すべてのグループからすべてのデータポイントを集めます。これにより、何も起こっていないと仮定した帰無仮説をシミュレートします。
- グループG₁に∣ G₁ ∣のポイントを重複せずに割り当て、グループG₂に∣ G₂ ∣のポイントを重複せずに割り当て、…、すべてのポイントが割り当てられるまで繰り返します。
- 元のサンプルで計算された興味のある統計量を計算し、結果を記録します。
- 上記の手順を多数回繰り返し、各回の興味のある統計量を記録します。
上記の手順は、興味のある統計量を持つ分布を作成します。観測された差以上の値を観測する確率がp値です。p値が大きい場合、偶然に観測された差が生じる可能性があり、まだ何も発見されていません。
「p値は、帰無仮説が真である場合に、観測された結果と同じように極端な結果を観測する確率と考えてください。」
上記の形式は非常に一般的です。例に戻ると、新薬用のグループと従来の治療用のグループの2つのグループしかありません。順列検定を実行するためのコードは以下の通りです。
私のマシンでは、約30秒かかる10,000回の順列を実行します。重要な質問は、どのくらいの頻度で偶然に新薬が従来の治療法よりも1.5%以上効果的になるのでしょうか?以下に、シミュレートされた効果の差のヒストグラムを示します。

赤いバーは、新薬が偶然に従来の治療法よりも効果的であると判断された場合を示しています。これはそれほど珍しくはありません。p値は0.1084です。有意水準a=0.05でテストを実行した場合、帰無仮説を棄却することはできません。この時点では何も祝うことはありません。パーティーを開催していた場合は中止する必要があります。または、延期するかもしれません。
「aを誤検出率と考えてください。つまり、帰無仮説が真である場合、実験を繰り返すときに5%の確率で統計的に有意な差があると結論付けることになります。」
楽観的になる理由があります。私たちが実行したA/Bテストには2つの可能な結果があります。効果がある場合(私たちの場合、新薬は従来の治療法よりも効果的である)、または効果がないと結論付ける十分な証拠がない場合です。テストは効果がないと結論付けません。新薬が結局はより効果的かもしれません。ただし、これはまだ選択した有意水準でデータを使用して証明することはできません。テストは、偽陽性(またはタイプ1エラーとも呼ばれる)から私たちを保護していますが、偽陰性(またはタイプ2エラーとも呼ばれる)かもしれません。これがチームの期待です。
もう一つ質問することができます。新薬が従来の治療法よりも効果的であると結論付けるためには、観測された差はどれくらい必要ですか?明らかに1.5%は十分ではありませんが、どれくらい必要ですか?答えは作成されたヒストグラムから容易に得ることができます。観測された差に対応する垂直線を右に「移動」し、赤いバーのテールが合計面積の5%を占めるようにします。つまり、95パーセンタイルnp.percentile(differences, 95)を使用します。これは0.0203または2.03%を示します。1.5%以上ですが、それほど大きくはありません。
有意水準0.05を使用すると、新薬の治療効果の増加が区間(-∞、0.0203]にある場合、帰無仮説は棄却されません。これは信頼区間とも呼ばれます。帰無仮説を棄却しない観測された統計量の値のセットです。5%の有意水準を使用したため、これは95%信頼区間です。新薬がより効果的ではないと仮定した場合、実験を複数回実行すると、効果の差は信頼区間内に95%の確率で含まれます。これが信頼区間が私たちに伝えることです。p値がaを超えるのは、信頼区間が観測された効果の増加を含んでいる場合に限り、つまり帰無仮説を棄却することができないということです。これらは当然、帰無仮説を棄却するかどうかをチェックする2つの方法です。
これまでの動物実験の数では、帰無仮説を棄却することはできませんが、信頼区間の境界からは遠く離れていません。チームは楽観的ですが、新しい薬がより効果的であるという説得力のある証拠をもっと集める必要があります。しかし、どれだけの証拠が必要なのでしょうか?次のセクションで再検討します。リサンプリングを使用したシミュレーションを実行することで、この質問にも答えることができます!
このセクションを結論付ける前に、p値を近似するために古典的な統計テストを使用することもできることを注意しておくことが重要です。上記に示された表は、二つの変数の相互関係を提供し、それらの間に相互作用があるかどうかを確立するために使用される、連関表としても知られています。二つの変数の独立性は、連関行列から始めてカイ二乗検定を使用して調べることができますが、双側検定を実行しないように注意が必要です(十分に試してはいませんが、scipyはデフォルトで双側検定を使用するようです。これにより、p値が高くなります)。統計ライブラリのユーザーガイドに入る前に、順列検定の実行方法を知っていると良いですね。
パワーの推定
確かに、新しい薬の効果の増大が統計的に有意であることを証明することができないという事実に失望するでしょう。それでも、新しい薬が本当により良いものである可能性は十分にあります。私たちはもっと多くの研究を行う意思がありますが、そのためにはどれだけの数の動物を必要とするのでしょうか?それがパワーの出番です。
パワーとは、与えられたサンプルサイズと有意水準に対して、ある効果の大きさを検出する確率です。新しい薬が従来の治療法に比べて治療の効果を1.5%増加させると予想するとしましょう。各治療法で3000匹の動物を治療し、有意水準を0.05に固定した場合、検定のパワーは80%です。つまり、実験を何度も繰り返すと、5回の実験のうち4回では新しい薬が従来の治療法よりも効果的であると結論づけることになります。言い換えると、誤った否定(第II種の誤り)の割合は20%です。上記の数値はもちろん仮想的なものです。重要なのは、サンプルサイズ、効果の大きさ、有意水準、パワーの4つの量が関連しており、そのうちの3つを設定することで4番目の量を計算できるということです。最も一般的なシナリオは、他の3つからサンプルサイズを計算することです。これがこのセクションで調査する内容です。単純化のために、各実験で新しい薬と従来の治療法で同じ数の動物を治療することを仮定します。
以下の手順では、サンプルサイズを関数としたパワーを持つ曲線を構築しようと試みます:
- 従来の治療を受けたと仮定される動物の合成データセットを作成し、治療の効果が私たちが知っている程度になるようにします(以下では、これを0.8034に設定しています)。
- 新薬を使用した治療を受けたと仮定される動物の合成データセットを作成し、調査したい効果の大きさを追加します(以下では、これを0.015および0.020に設定して効果を確認します)。
- 各合成データセットからサイズn_sampleのブートストラップサンプルを抽出します(以下では、これを3000、4000、5000、6000、7000の値に設定しています)。
- 前のセクションで確立したアプローチを使用して統計的有意性のための順列検定を実施し、治療の効果の差が統計的に有意かどうかを記録します。
- ブートストラップサンプルを生成し、治療の効果の差が統計的に有意である頻度を計算します。これが検定のパワーです。
これはもちろんより長いシミュレーションですので、ブートストラップサンプルの数は200に制限し、有意性検定の順列数も前のセクションと比べて500に減らしています。
このブートストラッピング/順列シミュレーションの実行には、控えめなマシンでは1時間程度かかり、この記事の範囲を超える並列処理の恩恵を受けることができます。結果をmatplotlibを使用して簡単に可視化することができます:
これにより、以下のグラフが生成されます:
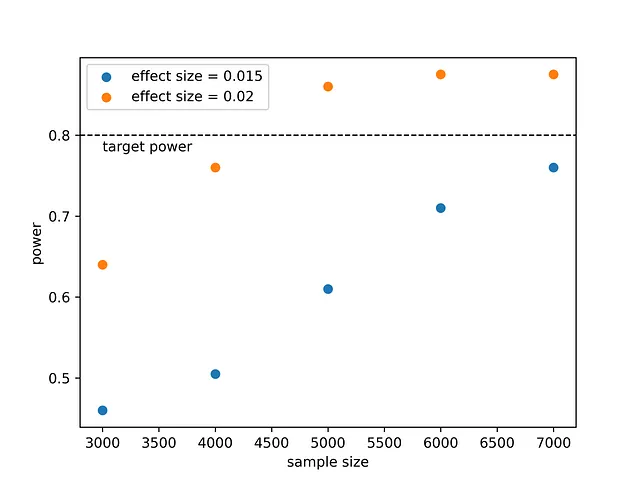
これから私たちは何を学びますか?新薬が1.5%効果的であると予想する場合、80%のパワーでこれを証明するためには7000匹以上の動物を治療する必要があります。効果の大きさが大きい場合、つまり2%であれば、約4500匹の動物で十分です。これは直感的です。大きな効果は小さな効果よりも検出しやすいです。このような大規模な実験を実施するかどうかを決定するには、コストと利益の分析が必要ですが、少なくとも新しい薬が効果的であることを証明するために必要な要件を知ることができます。
statsmodelsを使用して必要なサンプルサイズを計算することもできます:
これは以下を表示します:
効果サイズ:0.015、サンプルサイズ:8426.09効果サイズ:0.020、サンプルサイズ:4690.38シミュレーションの結果は一貫しているようです。シミュレーションでは、効果サイズが1.5%の場合に0.8のパワーに到達するには不十分な7000のサンプルサイズまで達しました。これはproportion_effectsize関数を使用しても確認できます。
結論
この記事をお楽しみいただけたことを願っています。個人的には、シンプルなブートストラップとパーミュテーションを使用してこれらの統計的概念を根本から調査できることを充実感を持っています。
閉じる前に、注意が必要です。この記事では、p値に重点を置いて扱っており、その信頼性がますます批判を受けています。真実は、歴史的にp値の重要性が誇張されてきました。p値は、データがヌルモデルまたはパーミュテーションテストとどれほど矛盾しているかを示すものです。p値は、代替仮説が真である確率ではありません。また、ヌル値を棄却できるp値が示されているからといって、効果の大きさが重要であるわけではありません。効果サイズが小さい場合でも統計的に有意であるかもしれませんが、その効果の大きさは重要ではありません。
参考文献
- Introductory Statistics and Analytics: A Resampling Perspective by Peter Bruce (Wiley, 2014)
- Practical Statistics for Data Scientists: 50+ Essential Concepts Using R and Python by Peter Bruce, Andrew Bruce, Peter Gedeck (O’Reilly, 2020)
- Interpreting A/B test results: false positives and statistical significance, a Netflix technology blog
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






