類似検索、パート5：局所性鋭敏ハッシュ（LSH）

Similarity Search Part 5 Locality Sensitive Hashing (LSH)

類似性情報をハッシュ関数に組み込む方法を探る

類似性検索とは、クエリが与えられた場合に、データベース内のすべてのドキュメントの中からそれに最も類似したドキュメントを見つけることが目的となる問題です。

はじめに

データサイエンスにおいて、類似性検索は、NLP領域、検索エンジン、または推薦システムなどで、クエリに対して最も関連性の高いドキュメントやアイテムを取得する必要がある場合に頻繁に現れます。大量のデータにおける検索性能を向上させるためのさまざまな方法が存在しています。

この記事シリーズの以前の部分では、逆ファイルインデックス、製品量子化、HNSWについて説明し、それらがどのように組み合わされて検索品質を向上させるかについて説明しました。この章では、高速な検索速度と品質を両立する原理的に異なるアプローチを見ていきます。

• AI医療診断はどのように動作しますか？
• AIの未来を形作る ビジョン・ランゲージ・プリトレーニング・モデルの包括的な調査と、ユニモーダルおよびマルチモーダルタスクにおける役割
• FastAPI、AWS Lambda、およびAWS CDKを使用して、大規模言語モデルのサーバーレスML推論エンドポイントを展開します

類似性検索、パート3: 逆ファイルインデックスと製品量子化のブレンド

このシリーズの最初の2つの部分では、情報検索における2つの基本アルゴリズム、逆…

towardsdatascience.com

類似性検索、パート4: 階層型ナビゲーション可能小世界（HNSW）

階層型ナビゲーション可能小世界（HNSW）は、最近傍探索のために使用される最新のアルゴリズムです。

towardsdatascience.com

ローカルセンシティブハッシング（LSH）は、データベクトルをハッシュ値に変換し、類似性に関する情報を保持しながら検索範囲を縮小するために使用される方法のセットです。

私たちは、3つのステップから構成される従来のアプローチについて説明します。

1. Shingling : オリジナルのテキストをベクトルにエンコードする。
2. MinHashing : ベクトルを特別な表現であるシグネチャに変換し、それらの類似性を比較するために使用できるようにする。
3. LSH関数 : シグネチャブロックを異なるバケットにハッシュ化する。ベクトルのペアのシグネチャが少なくとも1回同じバケットに入る場合、それらは候補と見なされます。

私たちは、この記事の中で、それぞれのステップの詳細について徐々に掘り下げていきます。

Shingling

Shinglingとは、与えられたテキスト上のk-gramを収集するプロセスです。k-gramは、k個の連続するトークンのグループです。文脈によって、トークンは単語または記号であることがあります。Shinglingの究極の目標は、収集されたk-gramを使用して、各ドキュメントをエンコードすることです。このために、one-hotエンコーディングを使用します。ただし、他のエンコーディング方法も適用できます。

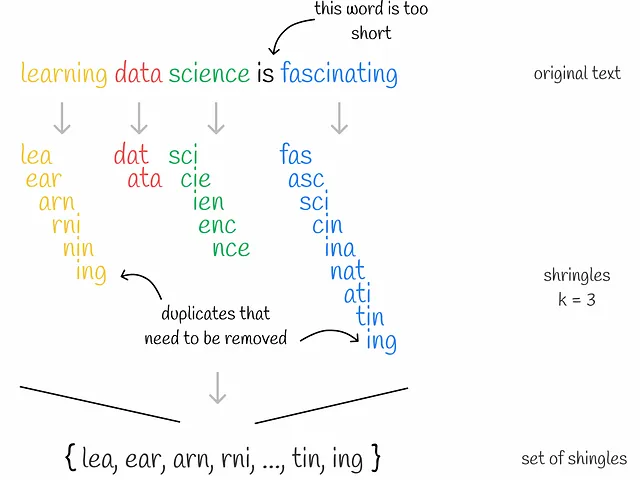
まず、各ドキュメントのユニークなk-gramが収集されます。次に、各ドキュメントをエンコードするために、すべてのドキュメントにおけるユニークなk-gramのセットを表すボキャブラリが必要です。その後、各ドキュメントについて、ベクトルの長さがボキャブラリのサイズと同じゼロのベクトルが作成されます。ドキュメント内の各出現するk-gramについて、その位置をボキャブラリ内で特定し、該当するドキュメントベクトルの位置に「1」を配置します。ドキュメント内で同じk-gramが複数回出現しても、問題ありません。ベクトル内の値は常に1になります。

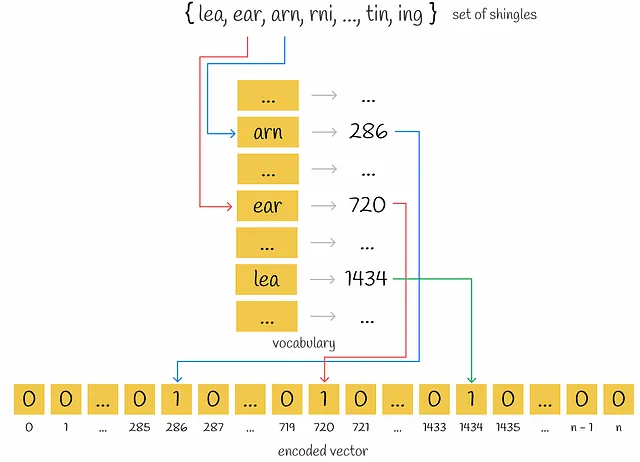
MinHashing

この段階では、初期テキストがベクトル化されました。ベクトルの類似性は、Jaccard指数を介して比較できます。2つのセットのJaccard指数は、両方のセットに共通の要素の数を、すべての要素の長さで割ったものと定義されます。

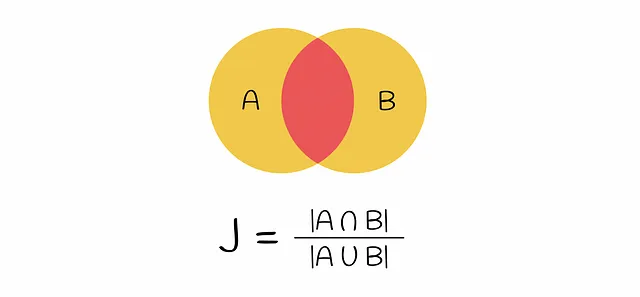
エンコードされたベクトルのペアを取ると、Jaccard指数の式での共通部分は、両方のベクトルに1を含む行の数（すなわち、k-gramが両方のベクトルに現れる）であり、和集合は、少なくとも1つの1を持つ行の数です（k-gramが少なくとも1つのベクトルに存在する）。

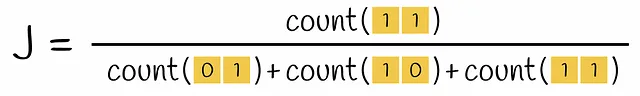
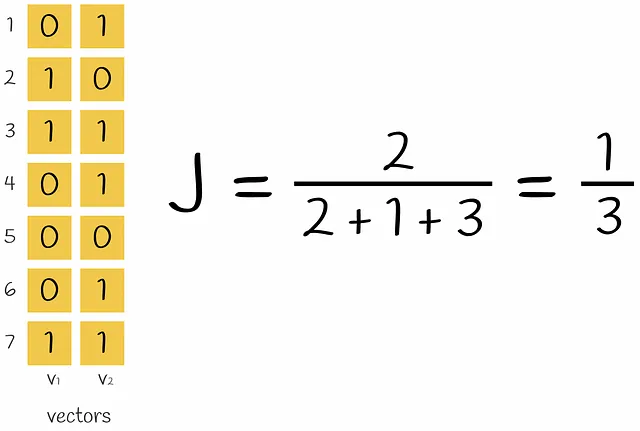
現在の問題は、エンコードされたベクトルのスパース性です。2つのone-hotエンコードされたベクトル間の類似性スコアを計算するには、多くの時間がかかります。それらを密な形式に変換すると、後で操作するのにより効率的になります。最終的に目標とするのは、これらのベクトルを小さな次元に変換し、その類似性に関する情報を保持する関数を設計することです。このような関数を構成する方法をMinHashingと呼びます。

MinHashingは、入力ベクトルのコンポーネントを置換し、最初のインデックスを返すハッシュ関数です。

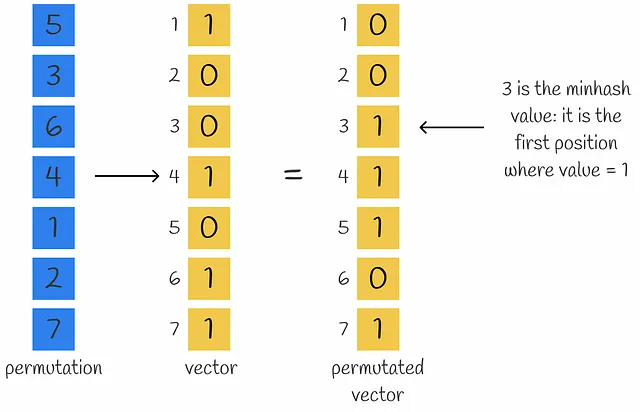
n個の数で構成されるベクトルの密な表現を得るには、n個のminhash関数を使用してn個のminhash値を取得し、signatureを形成します。

最初は明らかではないかもしれませんが、複数のminhash値を使用すると、ベクトル間のJaccard類似度を近似することができます。実際、使用されるminhash値が多ければ多いほど、近似度は高くなります。

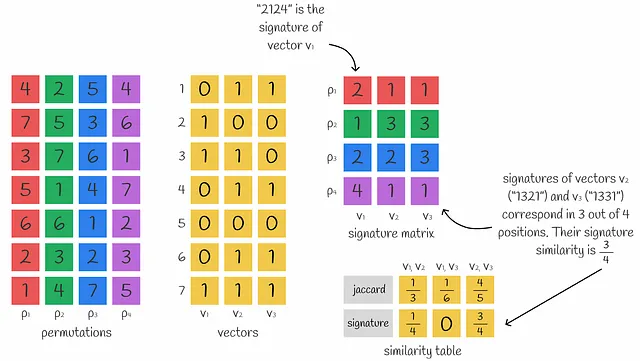
これは、ただの有用な観察です。実際には、背後に整理された定理があります。では、なぜsignatureを使用してJaccard指数を計算できるのかを理解しましょう。

定理の証明

あるベクトルのペアにおいて、01、10、および11のタイプの行のみが含まれていると仮定します。その後、これらのベクトルにランダムな置換を行います。すべての行に1が少なくとも1つ存在するため、ハッシュ値を計算する際には、対応するハッシュ値が1に等しいベクトルの最初の行で、少なくとも2つのハッシュ値計算プロセスのうちの1つが停止することになります。

2つ目のハッシュ値が最初の値と等しい確率はどの程度ですか？明らかに、2つ目のハッシュ値が1と等しい場合にのみそれが起こります。つまり、最初の行は11のタイプでなければなりません。順列がランダムに選択された場合、そのようなイベントの確率はP = count(11) / (count(01) + count(10) + count(11))に等しくなります。この式は、Jaccardインデックスの式とまったく同じです。したがって：

ランダムな行の順列に基づいて2つのバイナリベクトルの等しいハッシュ値を取得する確率は、Jaccardインデックスに等しい。

ただし、上記のステートメントを証明するにあたり、初期ベクトルに00のタイプの行が含まれていないと仮定しました。00のタイプの行は、Jaccardインデックスの値を変更しないことが明らかです。同様に、00のタイプの行を含めて同じハッシュ値を取得する確率も影響を受けません。たとえば、最初の並べ替えられた行が00の場合、minhashアルゴリズムはそれを無視して、行に少なくとも1つの1が存在するまで次の行に切り替えます。もちろん、00のタイプの行は、それらがない場合とは異なるハッシュ値を生成する可能性がありますが、同じハッシュ値を取得する確率は変わりません。

重要なステートメントを証明しました。しかし、同じminhash値を取得する確率をどのように推定できますか？明らかに、ベクトルのすべての可能な順列を生成して、すべてのminhash値を計算して、所望の確率を見つけることができます。明らかな理由から、これは効率的ではありません。サイズnのベクトルの可能な順列の数はn!に等しいためです。それにもかかわらず、確率は近似的に評価できます。多数のハッシュ関数を使用してその数のハッシュ値を生成するだけです。

2つのバイナリベクトルのJaccardインデックスは、それらのシグネチャの対応する値の数に近似します。

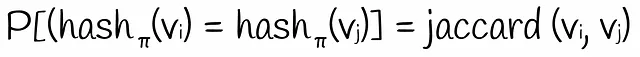
長いシグネチャを取ると、より正確な計算が得られることが簡単にわかります。

LSH関数

現時点では、類似性に関する情報を保持しつつ等しい長さの密なシグネチャに生のテキストを変換できます。ただし、実際には、このような密なシグネチャは通常、高次元になります。これらを直接比較するのは効率的ではありません。

長さが100のシグネチャを持つn = 10⁶のドキュメントを考えます。シグネチャの1つの数値が格納されるのに4バイトが必要であると仮定すると、全体のシグネチャには400バイトが必要です。n = 10⁶のドキュメントを保存するには、400 MBのスペースが必要です。これは現実的に実現可能です。ただし、ブルートフォースな方法で各ドキュメントを直接比較すると、おおよそ5 * 10¹¹の比較が必要になります。これは、nがさらに大きい場合には、特に多すぎます。

問題を回避するために、ハッシュテーブルを構築して検索パフォーマンスを高速化することができますが、2つのシグネチャが非常に似ており、1つの位置のみが異なる場合でも、異なるハッシュを持つ可能性があります（ベクトルの余りは異なる場合があります）。しかし、通常はそれらが同じバケットに含まれるようにしたいと思います。これがLSHの役割です。

LSHメカニズムは、少なくとも1つの対応する部分を持つ場合、ペアのシグネチャを同じバケットに配置する複数の部分から構成されるハッシュテーブルを構築します。

LSHは、署名行列を取り、等しいb部分で水平に分割したバンドと呼ばれるr行を含む部分に分割します。署名を単一のハッシュ関数に差し込む代わりに、シグネチャはb部分に分割され、それぞれのサブシグネチャは独立にハッシュ関数によって処理されます。その結果、各サブシグネチャは別々のバケットに入ります。

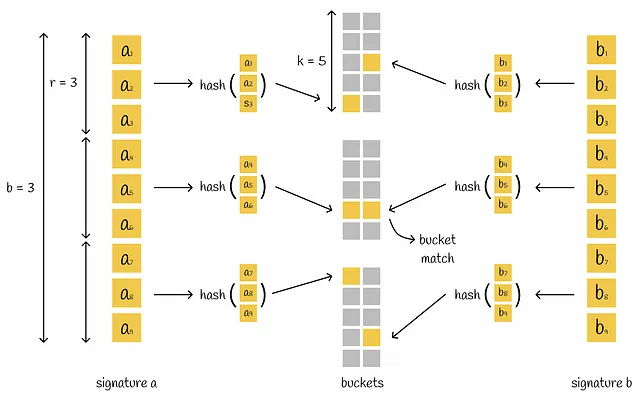
2つの異なるシグネチャの対応するサブベクトル間に少なくとも1つの衝突がある場合、シグネチャは候補と見なされます。見るとわかるように、この条件はより柔軟であり、ベクトルを候補とするには完全に等しくなる必要はありません。ただし、これにより偽陽性の数が増加します。異なるシグネチャのペアは、対応する部分が1つだけであっても、全体的には完全に異なる場合があります。問題に応じて、パラメータb、r、kを最適化することが常に良いでしょう。

エラーレート

LSHを使用すると、類似度がsの2つのシグネチャが、各バンドの行数rとバンド数bが与えられた場合に、候補として考慮される確率を推定できます。数段bと行rの数を見つけましょう。

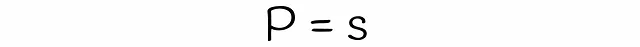
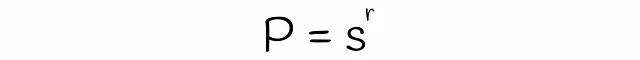
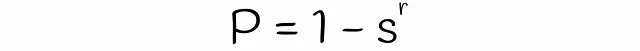
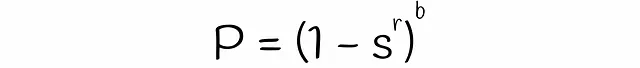
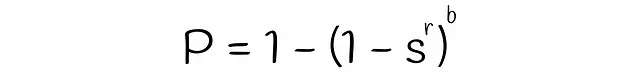
異なるサブベクトルが偶然同じバケットにハッシュされた場合の衝突は考慮されていないことに注意してください。そのため、シグネチャが候補である実際の確率はわずかに異なる場合があります。

例

私たちが剛体に適用した式をよりよく理解するために、簡単な例を考えてみましょう。7つの行を持つ5つのバンドに等しく分割された長さ35の2つのシグネチャを考えます。以下の表は、Jaccard類似性に基づく少なくとも1つの等しいバンドを持つ確率を表します。

2つの類似したシグネチャのJaccard類似度が80％である場合、93.8％の場合に対応するバンドがあります（真陽性）。残りの6.2％のシナリオでは、そのようなシグネチャのペアは偽陰性です。

ここで、2つの異なるシグネチャを取ります。例えば、彼らは20％しか似ていません。したがって、彼らは0.224％の場合にだけ偽陽性候補です。99.776％の場合、彼らは似たようなバンドを持っていないので、真陰性です。

視覚化

ここで、類似度sと2つのシグネチャが候補になる確率Pの間の接続を視覚化しましょう。通常、シグネチャの類似度が高いほど、シグネチャが候補になる確率が高くなるはずです。理想的には、以下のようになります。

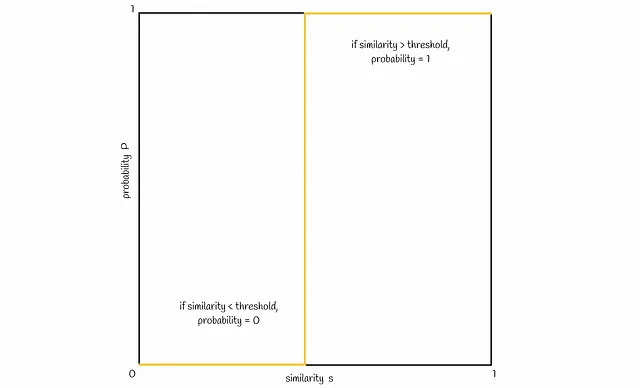
上記で得られた確率式に基づいて、典型的な直線は以下の図のようになります:

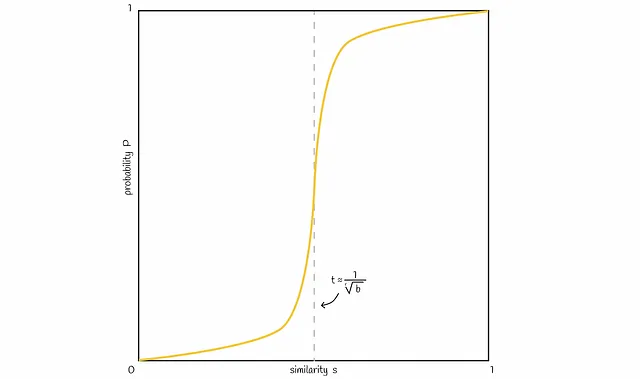
バンド数bを変化させることで、図内の線を左右にシフトすることができます。bを増やすと線は左に移動し、より多くのFPを引き起こし、減らすと右にシフトし、より多くのFNを引き起こします。問題に応じて、良いバランスを見つけることが重要です。

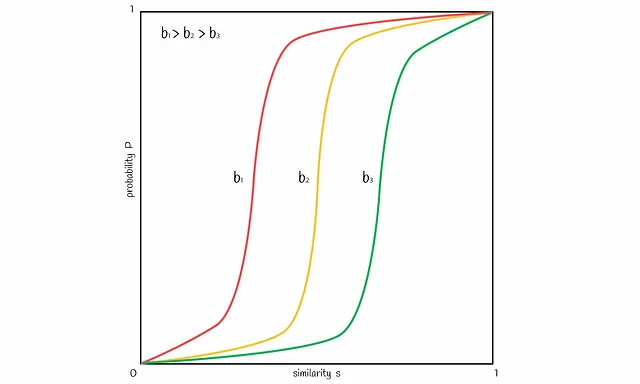
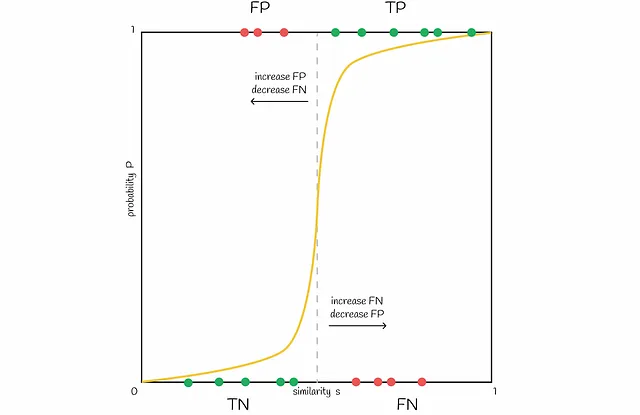
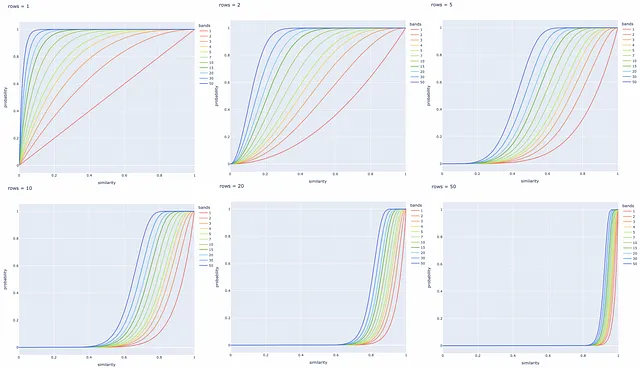
異なるバンド数と行数での実験

異なるbとrの値に対して以下にいくつかの直線プロットが作成されます。特定のタスクに基づいてこれらのパラメータを調整して、類似したドキュメントのペアをすべて取得し、異なるシグネチャを持つものを無視することが常に良いです。

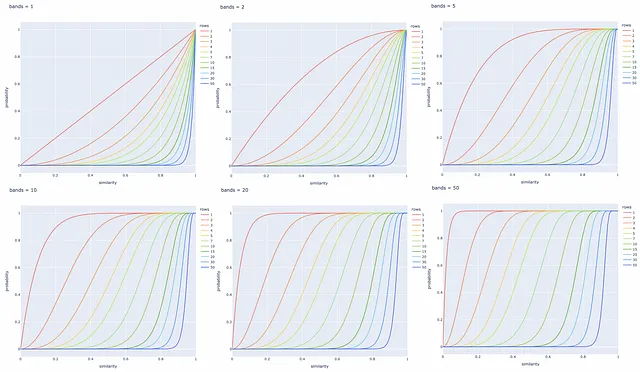
結論

LSH法のクラシックな実装を紹介しました。LSHは、低次元のシグネチャ表現と高速なハッシングメカニズムを使用して、候補の検索範囲を縮小することにより、検索速度を大幅に最適化します。同時に、これは検索精度の犠牲になりますが、実際には差はほとんど無視できます。

ただし、LSHは高次元データに対して脆弱です。より多くの次元は、良好な検索品質を維持するためにより長いシグネチャの長さとより多くの計算を必要とします。このような場合は、別のインデックスを使用することをお勧めします。

実際に、LSHの異なる実装が存在しますが、すべてが入力ベクトルをハッシュ値に変換して、類似性に関する情報を保持するという同じパラダイムに基づいています。基本的に、他のアルゴリズムはこれらのハッシュ値を取得する他の方法を定義するだけです。

ランダム投影法は、次の章で説明するLSH法の別の方法であり、類似性検索のためのLSHインデックスとしてFaissライブラリで実装されています。

リソース

• Locality Sensitive Hashing | Andrew Wylie | December 2, 2013
• Data Mining | Locality Sensitive Hashing | University of Szeged
• Faiss repository

すべての画像は、特に注記がない限り、著者によるものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!