「ルービックとマルコフ」

Rubik and Markov

ここでは、ルービックキューブを最適に解く確率を求めます

ルービックキューブは、巨大な状態空間とただ1つの解を持つ計画問題のプロトタイプです。まさに難解な問題です。ガイダンスがなければ（1秒に100回もフェイスを回せるとしても）、宇宙の寿命を費やしても成功しないかもしれません。それに関わるすべての要素は非常に大きな数に関連しているように思われます。

ここで計算する量はその例外です。これにより、困難な問題（および同様の計画問題）に対する簡単な視点が得られます。2つの要素、ランダムプロセスと最適ソルバーが必要です。最後のものは、任意の初期状態を与えられた場合に、最小の手数でキューブ（または類似の問題）を解くことができる（現実的または理想的な）デバイスです。以下の質問に完全に答えます：

解かれたキューブがN回のランダムな回転を行った場合、最適なソルバーがそれを元に正確にd手で解く確率p(d|N)は何ですか？

通常の状況では、誰かがキューブを解くように頼まれた場合、それは参照やラベルのないシャッフルされたキューブだけです。ここでは、シャッフルされた状態に関する1つの情報があります：それは解かれた状態からN回のランダムな動きを行った後に得られました。その情報は有用です！

• 文の補完のための言語モデル
• 2023年にディープラーニングのためのマルチGPUシステムを構築する方法
• 「言語モデルは自分自身のツールを作ることができるのか？」

なぜp(d|N)に興味があるのですか？

計算的には、異なる方法でキューブを解読することができます。ルービックプロジェクトの野心は、いくつかの状態を効率的に解くことから、可能な状態すべてを最適に解くことまでの範囲に及ぶかもしれません（これには有名な35CPU年がかかります）。キューブソルバーには、通常2つの要素が関与します。探索アルゴリズムとヒューリスティック関数です。これら2つを選択することで、アプローチの難易度、効率性、または計算的要求をパラメータ化します。

ヒューリスティック関数の領域では、つまり探索ガイダンスの領域では、常に新しいアイデアの余地があります。歴史的には、キューブのヒューリスティックは、解かれた位置に対するスクランブルされたキューブフェイスレットのマンハッタン距離の推定値の組み合わせでした。最近では、ヒューリスティックとしてニューラルネットが使用されました。

ニューラルネット＝ルービックキューブの新しいヒューリスティック

ニューラルネットの作業は単純です（分類器）：キューブの状態xとその状態の深さdが予測されます。状態の深さdは、その状態を最適に解くために必要な最小手数で定義されます。次のことに注意してください。任意の状態の深さを知っているデバイスを持っている場合、実際には最適なソルバーを持っています。なぜなら、常に深さがより低い状態を与える動きを選択できるからです。深さ= 0（解かれた状態）に到達するまで。

問題は、そのネットをトレーニングする方法です。具体的には、正確なトレーニングデータを取得する方法です。解かれた状態xの正確な深さを知る簡単な方法はありません。最適なソルバーを既に持っている場合を除いては。そして私たちには最適なソルバーがありません、または、計算コストの高いものを使用したくありません。ゼロから近似的かつ効率的な最適ソルバーを構築し、それに対して正確なトレーニングデータを取得したいのです：

training_data = (x , d).

言ったように、dの正確さは難しいですが、特定のシャッフルされた状態にいくつかの番号Nを関連付けることは簡単です：それは解かれた状態にN回のランダムな動きを加えて生成されたものです。その後

p(d|N)は、Nが与えられた場合のdを推定します。

p(d|N)は、そのトレーニングデータの正確さを向上させるために使用されます。前述の論文の著者たちは、最初のルービックキューブの深度分類ニューラルネットを構築しました。彼らのトレーニングデータは次の形式でした：

training_data = (x , N).

彼らはNとしてdを取りました。 その選択は、訓練中にベルマンのようなループを使用してラベルの正確性を動的に改善することによって補償されました。ここで計算される確率p(d|N)は、トレーニングデータの正確性の出発点をより良く提供します（解かれた状態をランダムに回転させたものを豊富に取得することによって得られました）。

ランダムウォークの視点

p(d|N)を計算することは、ランダムウォーカーがNステップ後にどれだけ遠くまでdになるかを尋ねることと同じです。正方形の格子ではなく、10の19乗のノード（キューブの状態）と同じ数のリンク（合法的な手順）を持つ巨大なルービックグラフを歩くことになります。ノードがその深さによって整理されるようなレイアウトを選ぶことで、解かれた状態が中央にあり、深さdの状態が中央から半径dの位置にあるような対称的なグラフになります。半径（深さ）の方向は非常に簡単な視点を提供します。

慣例

ここでは、3x3x3キューブのための四半回転メトリックを採用しています。移動は、時計回りまたは反時計回りの90度の面回転を含みます。このメトリックでは、12種類の移動が可能です。半回転メトリック（180度の面回転も1つの移動として含む）など、異なるメトリックを選んだ場合、p(d|N)の式は異なるものになります。

データ

p(d|N)を取得するには、何らかのドメイン知識を使用する必要がありますが、グラフ、パターンデータベース、群論といったものは扱いたくありません。もっと「基本的な」ものを使用します：

深さdにおけるキューブの状態の人口を含むリスト。

（2012年の「神の数」の論文の著者によって提供された）リストには、ある深さの状態がどれだけあるかが指定されておらず、Nに関する言及もありません。

# Depth population list# number of cubes' states at a depth d in the quarter-turn metric      D_d={# depth  number of states  0:     1,  1:     12,  2:     114,  3:     1068,  4:     10011,  5:     93840,  6:     878880,  7:     8221632,  8:     76843595,  9:     717789576,  10:    6701836858,  11:    62549615248,  12:    583570100997,  13:    5442351625028,  14:    50729620202582,  15:    472495678811004,  16:    4393570406220123,  17:    40648181519827392,  18:    368071526203620348,  19:    3000000000000000000,  # approximate  20:    14000000000000000000, # approximate  21:    19000000000000000000, # approximate  22:    7000000000000000000,  # approximate  23:    24000000000000000,    # approximate  24:    150000,               # approximate  25:    36,  26:    3,  27:    0}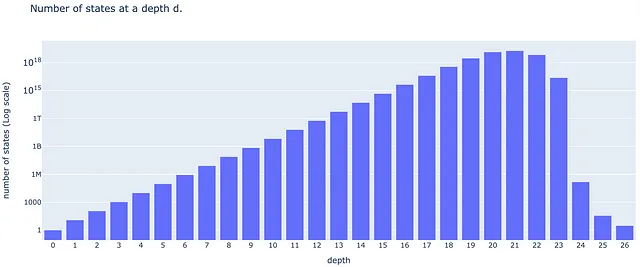

このリストに関するいくつかの観察：

まず、深さ26以上の状態は存在しません（四半回転メトリックにおける「神の数」は26です）。次に、リストは19から24のdに対しておおよその状態数を報告しています。後でこれに注意する必要があります。三番目に、対数スケールのグラフを作成すると、ほとんどの深さで線形な成長が見られます（終わりに近い深さを除く）。これは、状態の人口D(d)が指数関数的に成長していることを意味します。対数グラフの直線部分を直線にフィットさせることで、d = 3からd = 18の間の状態の人口が成長することを学びます。

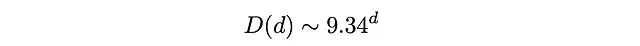
深さ3 < d < 18では、平均して、12の動作のうち9.34は解決状態から遠ざかり、2.66は近づくでしょう。

深さのクラスにおけるマルコフ過程

p(d|N)を見つけるために、深さのクラスをマルコフ過程のサイトとして想像します。説明しますね：

深さクラスdは、解決状態までの最小移動数がdであるすべてのキューブの状態の集合です。深さクラスdでランダムに状態を選び、ランダムな移動でランダムな面を回すと、確率p_dでクラスd + 1の状態を得るか、確率q_dでクラスd – 1の状態を得ることができます。四半回転メトリックでは、自己クラスの移動はありません。

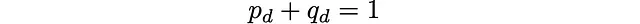
これはマルコフ過程を定義します。特定のサイトは深さクラス全体です。私たちの場合、隣接する深さクラスのみが1つのジャンプで接続されています。正確には、これは離散時間の誕生 – 死亡マルコフ連鎖です。サイトの数が有限であるため、連鎖も既約であり、エルゴード性を持ち、一意の定常分布が存在します。

各時刻におけるランダム移動の選択については、確率が均等に分布していると仮定します。これにより、深さクラス間のいくつかの遷移確率p_d, q_d（計算する必要があります）が誘導されます。ランダムな移動の数Nは、マルコフ過程の離散時間です。これも一次元のランダムウォーカーです。各サイト（深さクラス番号d）で、前に進む確率はp_dであり、後ろに進む確率はq_dです。この一次元の連鎖は、おおよそ言えば、ルービックのグラフの「放射状」の方向（深さ放射状レイアウトで構成されています）。

遷移行列

任意のマルコフ過程は、遷移行列Mにエンコードされます。 Mの（i,j）のエントリは、サイトiからサイトjへのジャンプの確率です。私たちの場合、次のエントリのみがゼロとは異なります：

ここでp_0 = 1: 深さクラス0（解決状態だけを含む）からは、深さクラス1にのみジャンプできます（クラス-1は存在しません）。また、q_26 = 1：深さクラス26からは、深さクラス25にのみジャンプできます（クラス27は存在しません）。同じ理由で、p_26またはq_0はありません。

定常分布

キューブをランダムに動かす行為を、一次元の深さクラスのランダムウォーカーが確率q_dとp_dで前後に跳ねることに対応させました。長い散歩の後に何が起こるのでしょうか？ある特定の場所をウォーカーが長い散歩の後に何回訪れるのでしょうか？現実世界では、ランダムなターンを経験するキューブが深さクラスを訪れる頻度はどれくらいでしょうか？

長い期間をかけて、そしてどの出発点であっても、ウォーカーが深さクラスdに滞在する時間は、その深さクラスの人口D(d)に比例します。これがここでの主なポイントです。

（正規化された）深さ人口リストD(d)は、深さクラスのマルコフ過程の定常分布を表すベクトルとして解釈する必要があります。

数学的には、D(d)はMの左固有ベクトルです。

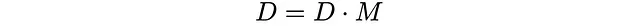
この行列方程式からは26個の線形方程式が得られ、そこからp_i’とq_iを得ることができます。

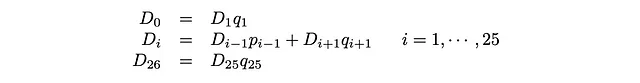
p_0 = q_26 = 1とすると、これを以下のように書き直すことができます。

これらは詳細なバランス方程式として知られています。定常サイト人口と跳躍確率の積であるフラックスは、両方向で同じです。解は次のようになります。

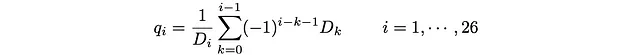
また、p_iはp_i + q_i = 1を使用して求められます。

深さクラスの人口に関するいくつかの条件

これらの解には興味深い点があります。確率であるため、q_iは次のような条件を満たす必要があります。

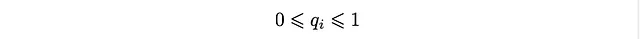
そして、分布D_kに対する以下の条件を導きます。

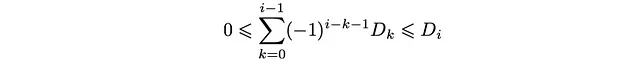
これは、深さ人口D_kが満たすべき不等式の連鎖です。具体的には、次のように整理することができます。

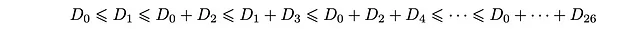
特に、最後の2つの不等式は次のようになります。

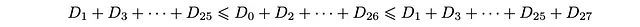
D_27 = 0であるため、下限と上限は等しくなります。したがって、次のようになります。

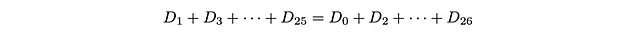
または：

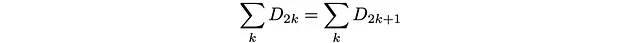
偶数番目のサイトの人口の合計は、奇数番目のサイトの人口の合計と等しくなければなりません！

これは、偶数と奇数のサイト間の詳細なバランスと見ることができます。すべての移動は常に異なる連続した深さクラスに行われます。どのジャンプも奇数の深さクラス（すべての奇数の深さクラスのクラス）から偶数の深さクラス（すべての偶数の深さクラスのクラス）に移動します。したがって、奇数から偶数のクラスへのジャンプは確率1で発生します（逆も同様です）。確率がどちらの方向でも1であるため、詳細バランスにより、それらの集団は等しくなければなりません。

同じ理由で、マルコフ過程は移動ごとに偶数と奇数のサイトを切り替える周期2の「定常分布」に到達します（離散時間N）。

データの問題

使用するデータのソースで報告されている深さ-人口D_dは、d = 19,20,21,22,23,24の場合においておおよその値です。したがって、これらの条件（不等式）をすべて満たす保証はありません。[0,1]の範囲外の確率q_iが得られることに驚かないでください（実際の場合です！）。特に、最後の条件（偶数-奇数の人口の均等性）を試して確認すると、大きな数値でオフになります！（更新：最後のノートを参照）

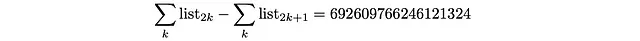
解決策

奇数クラスは人口が少ないようです（これは、著者がデータを報告する際に選んだ近似の結果です）。[0,1]の範囲の確率を得るために、最も人口が多い深さクラス21（最も少ない数値の追加を気付く深さクラス）の人口に前述の大きな数値を追加することを決定しました。この修正により、すべての得られた確率が正しいようです（つまり、不等式も満たされます）。

ジャンプの確率は次の通りです：

p_i = {1., 0.916667, 0.903509, 0.903558, 0.903606, 0.903602, 0.90352, 0.903415, 0.903342, 0.903292, 0.903254, 0.903221, 0.903189, 0.903153, 0.903108, 0.903038, 0.902885, 0.902409, 0.900342, 0.889537, 0.818371, 0.367158, 0.00342857, 6.24863*1e-12, 0.00022, 0.0833333}# iは0から25q_i = {0.0833333, 0.0964912, 0.0964419, 0.096394, 0.0963981, 0.0964796, 0.096585, 0.096658, 0.0967081, 0.0967456, 0.0967786, 0.0968113, 0.0968467, 0.0968917, 0.0969625, 0.0971149, 0.0975908, 0.0996581, 0.110463, 0.181629, 0.632842, 0.996571, 1., 0.99978, 0.916667, 1.}# iは1から26

ほとんどすべての最初のp_i（i = 21まで）は1.に近いです。これらは解かれた状態から離れる確率です。解かれた状態に近づく確率（q_i）は、iが21より大きい場合、ほぼ1です。これがキューブを解くのが難しい理由を明らかにします：ランダムウォーカー（またはキューブのランダムムーバー）は、深さクラス21の近くに「永遠に閉じ込められて」しまいます。

p(d|N)

​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​

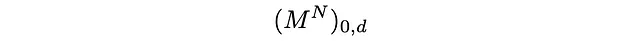
これが私たちが探していた確率です：

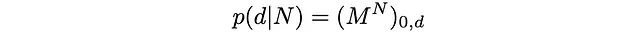
数値的には、p(d|N)はNとdが同じ偶奇性を持つ場合にのみゼロでないことがわかります（これはいくつかのルービックキューブの研究者によってよく知られています）。以下では、異なるNに対するいくつかのp(d|N)をプロットしています：

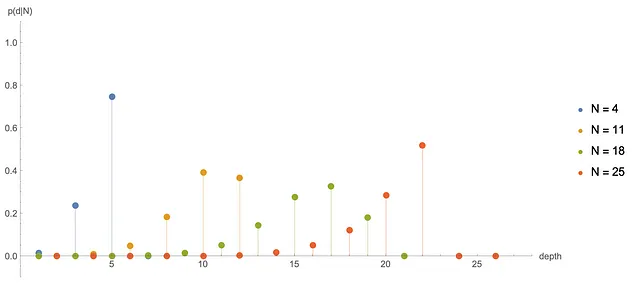
私たちは、N = 31または32の後に、p(d|N)が定常分布D(d)に非常に近いことを観察します（ただし、偶数と奇数のサイトの間を交互に切り替えます）。これは、キューブを本当にかき混ぜたと言うために必要な動きの回数に関する別の答えです。

ここで、私たちは逆問題を解決しました。定常分布から遷移確率を得ました。これは一般的なマルコフ過程では不可能です。特に、半回転メトリックでは、ここで説明した方法で半回転メトリックのp(d|N)を見つけることはできません。半回転メトリックは異なるのです。なぜなら、動きの定義により、同じ深さクラスにとどまることができるからです。これらの自己深さクラスのジャンプは、遷移行列の対角線上に追加の確率r_iを導入し、方程式よりも変数が多くなります。

最終コメント

ルービックキューブは計算上は35 CPU年の問題ですが、それについては解析的にまたはわずかな数値的な努力で記述できる側面が多くあります。ここで計算した確率はその一例です。私たちが言ったことは、より複雑なルービックキューブの類似品に簡単に一般化できます。クールな一般化は、より多くの次元に移ることです：S = 4次元、5次元、6次元などの次元のルービックキューブです。これらの場合、状態空間はSとともに指数関数的に成長します。つまり、マルコフ連鎖は望み通りの長さになるキューブがあります。言い換えれば、私たちは、次元Sに応じて状態の対数の対数である「神の数」がどれほど大きくなるかを説明するための特定の限界を取ることができます。

大きな「神の数」Gの限界では、確率p(d|N)は二項分布に近づくはずです。

なぜそうなるのかは、それがなぜそうであるかを見るのはあまり難しくありません。もしGが大きいなら、ほとんどのdに対してD_dの指数的な成長は非常に安定するでしょう。これは、大胆な、しかし過度に乱暴な推測です：

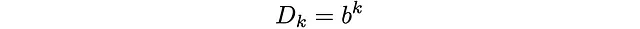
ただし、kが0とGから離れている場合には、1/(b+1)に近づくはずです。先ほど言ったように、S = 3Dの場合はb = 9.34です。より高いSの場合、bは増加するはずです（より多くの面は分岐係数bを増加させます）。これは、確率の次の値に変換されます：

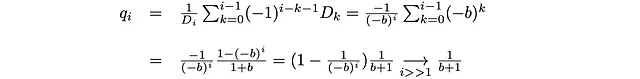
q_iは、原点から離れた場合（i>>1）および神の数（i<<G）に対して定数値1/(b+1)に近づきます。この範囲では、p_iも定数になります。ここで、3Dの場合のp_iとq_iの値は、i=3, …, 15,に対してほぼ一定であり、q_iはおおよそ1/(b+1)と等しいことがわかります（ただし、b = 9.34）。0 << i << Gの場合、我々は定数の確率で前進（p）と後退（q）を行う一次元のランダムウォーカーを持つことになります。この場合、ウォーカーの位置は二項分布に似た分布によって記述されます。

ランダムウォーカーがkステップ右に進む確率（成功率p）とN-kステップ左に進む確率（成功率q）を経てN回の試行後、Binomial(k,N,p)で表される確率が存在します。その後、Nステップ後の移動距離は次のようになります：

d = k – (N – k)

これにより、次のような解析的な推定値を求めることができます：

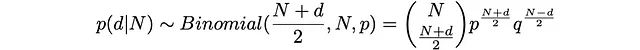
さらに、次のような興味深い事実があります：立方体の次元Sが増えると、分岐係数bが増加し、最も確率が高い深さdが実際にNに近づくということです。

更新ノート：この記事が公開された後、私は2012年の半回転メトリックにおける神の数が20であることを証明した論文の著者であるTomas RokickiとMorley Davidsonに、彼らの報告されたD(d)とそれを使用した負の確率について連絡を取りました。彼らは深さd = 19、…、24の人口の下限と上限を持つより正確なデータを共有してくれました。彼らのデータは、ここで得られた不等式とも、四半回転メトリックにおける偶数深さクラスの人口と奇数深さクラスの人口が等しいこととも互換性があります。この新しいデータを使用すると、ここで計算された確率には無視できる修正があります。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!