「RNNにおける誤差逆伝播法と勾配消失問題（パート2）」

RNNの誤差逆伝播法と勾配消失問題（パート2）

LSTMにおける勾配消失の解決方法

このシリーズの第1部では、RNNモデルでのバックプロパゲーションについて説明し、数式と数値を用いてRNNでの勾配消失問題を説明しました。この記事では、LSTMを使用して勾配消失問題を一部解決する方法を説明します。完全に解消されない場合や非常に長いシーケンスの場合でも、問題はまだ存在します。

動機

このシリーズの第1部で見たように、バニラRNNは隠れ状態に時間情報を格納します。新しい情報、つまりシーケンス内の新しいトークンが処理されるたびに、隠れ状態が更新されます。隠れ状態は各ステップで更新されるため、古い情報は上書きされ、ネットワークは過去に見たものを忘れてしまいます。これを避けるためには、別個のメモリと、新しい情報がある場合に何を書き込むか、将来に役立たない過去の情報を削除するためのメカニズムが必要です。LSTMはまさにそれを行います。LSTMは、長期的な情報を格納するメモリセルを追加し、過去の情報を忘れるためのゲートメカニズムを持っています。また、現在の入力から追加する情報を決定し、次の状態に渡す機能も持っています。

順方向伝播

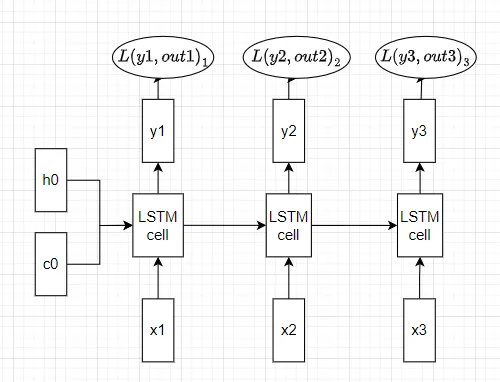
LSTMモデルでの時間に沿った順方向伝播の方法を見てみましょう。N個のトークンからなるシーケンスが与えられ、前のセルからメモリセルc(t-1)と隠れ状態h(t-1)を受け取ったと仮定します。時間ステップtで新しい入力情報をどうするかを決定するために、まず活性化を計算します。

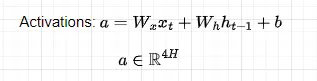
• 「このAI論文は、ChatGPTにペルソナを割り当てると、毒性が最大6倍に増加することを示しています」
• ドリームティーチャーというAIフレームワークに出会ってください：自己教師付きの特徴表現学習AIフレームワークであり、下流の画像バックボーンの事前トレーニングに生成ネットワークを利用します
• 「大規模な言語モデルを使用した生成型AI：実践トレーニング」

すべての重みは時間ステップ間で共有されることに注意してください。活性化行列は、4つの行列に分割され、それぞれの次元がHであることを適用し、最初の3つにはシグモイド活性化関数を、最後の行列にはtanh関数を適用してゲートを計算します。

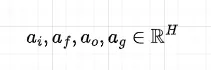
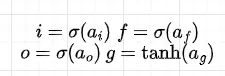
すべてのゲートが入力と前の隠れ状態の関数であることに注意してください。

最後に、次のステップに渡される現在のメモリセル状態c(t)と隠れ状態h(t)を計算します。

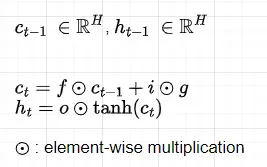
計算されたゲートの値は以下の機能を持ちます：

• ゲートf：前のメモリセルc(t-1)から忘れる情報。ゲートfはシグモイド活性化関数により0から1の間の値を含むため、要素ごとの乗算を行うと（c(t-1)とh(t-1)はベクトルであることを覚えておいてください）、fの値が0に等しいか0に近い場合、c(t-1)の情報はキャンセルまたは削減され、fの値が1に等しいか1に近い場合、情報はすべてまたはほぼすべて保持されます。
• ゲートg：前のメモリセルc(t-1)と組み合わされるメモリセル更新ベクトルとして解釈できます。他のゲートとは異なり、活性化関数a(g)にはtanh関数が適用され、出力は-1から1の値です。これにより、セルメモリの状態が増加または減少することが可能になります。シグモイド活性化関数がある場合、メモリセルの要素は決して減少しないためです。
• ゲートi：メモリセル更新ベクトル（ゲートg）から前のメモリセルc(t-1)に書き込む情報。
• ゲートo：新しい隠れ状態h(t)に含める情報。

これらのゲートは、図4に示されているように組み合わされて、新しいメモリセルc(t)と隠れた状態h(t)を計算するために使用されます。これらの新しいセルと隠れた状態は、同じプロセスを繰り返す次のLSTMセルに渡されます。このプロセスは以下の図で示すことができます：

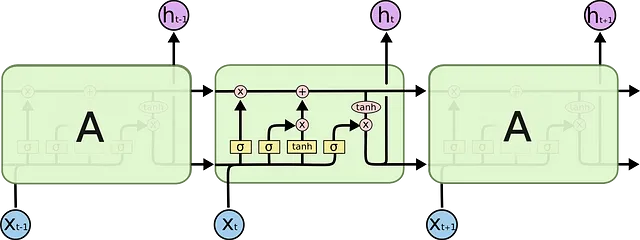
その後、各隠れた状態に対して、出力と損失を計算します：

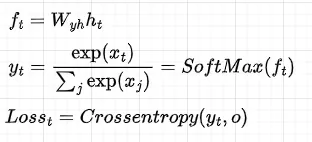
コードでは以下のようになります：

def softmax(x, axis=2):    p = np.exp(x - np.max(x, axis=axis,keepdims=True))    return p / np.sum(p, axis=axis, keepdims=True)def lstm_step_forward(x, prev_h, prev_c, Wx, Wh, b):    next_h, next_c, cache = None, None, None        h = x @ Wx + prev_h @ Wh + b    assert h.shape[-1] % 4 == 0    ai, af, ao, ag = np.array_split(h, 4, axis=-1)    i = sigmoid(ai)    f = sigmoid(af)    o = sigmoid(ao)    g = np.tanh(ag)    next_c = f * prev_c + i * g     next_h = o * np.tanh(next_c)        cache = (x, next_h, prev_h, prev_c, Wx, Wh, h, np.tanh(next_c), i, f, o ,g)    return next_h, next_c, cachenp.random.seed(232)# N - バッチサイズ# D - 埋め込み次元# V - 語彙サイズ# H - 隠れた次元# T - タイムステップN, D, T, H, V = 2, 5, 3, 4, 4x  = np.random.randn(N, T, D)h0 = np.random.randn(N, H)Wx = np.random.randn(D, H)Wh = np.random.randn(H, H)Wy = np.random.randn(H, V)b  = np.random.randn(H)y = np.random.randint(V, size=(N, T))mask = np.ones((N, T))all_cache = []h = np.zeros((N, T, H))    next_c = np.zeros((N, H))    for t in range(T):    xt = x[:, t , :]    if t == 0:        next_h, next_c, cache_s = lstm_step_forward(xt, h0, next_c, Wx, Wh, b)        all_cache.append(cache_s)    else:        next_h, next_c, cache_s = lstm_step_forward(xt, next_h, next_c, Wx, Wh, b)           all_cache.append(cache_s)    h[:, t, :] = next_h ft = h @ Wyout = softmax(ft)

バックプロパゲーション

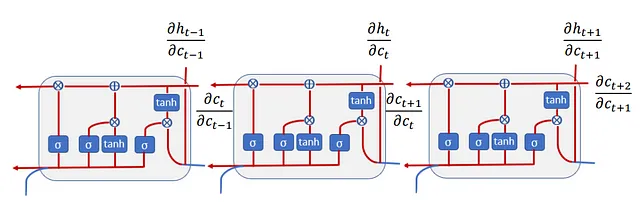
バックプロパゲーションの式は、通常のRNNの式よりも少し複雑です。このチュートリアルでは、Wxに関する勾配を導出し、その後でLSTMが消失勾配を処理する方法を示します。他のパラメータに関する導関数も同様に導出することができますが、読者の練習問題とします。ただし、コードにはすべての勾配に関する導関数が含まれており、コードに基づいて結果を確認することができます。損失に対する隠れた状態の導関数は、RNNと同じであり、そこでは何も変わりません：

他の単一コンポーネントに対する導関数を見つけましょう：

便宜上、dct/datとdht/datを分け、dht/dct dct/datの部分はdht/datとして直接書きます。また、行列形式で逆伝播を行うため、ゲートの導関数を次のように連結します：

dht/datの和は、前のセルに入る方向と隠れた状態に入る方向の2つがあるためです（図7を参照）。勾配の流れのロジックと同様に、dct/dc(t-1)の導関数は次のようになります：

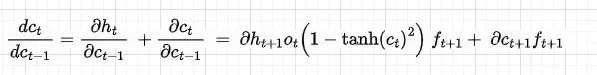
さて、Wxに関する全体の勾配を導出しましょう。これは、このシリーズのパート1で説明されているように、Wxに関する単一の損失の合計として与えられます：

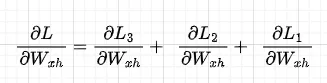
個々の損失に焦点を当てると、例えば、dL3/dWxでは、L3からWxに伝播するとき、すべての時間ステップの成分にWxが現れるため、これらの成分をすべて合計する必要があります。数学的な表記をやや乱用して、次のようなことをしています（Wx3 = Wx2 = Wx1を忘れないでください）：

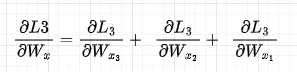
最初の成分は次のようになります。また、dht/dct dct/datをdht/datと置き換え、その導関数を直接使用します

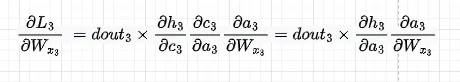
簡潔さのために、dL3/dWx2は省略し、直接第3成分に移ります。次のようになります：

前述のように、dht/dct dct/datをdht/datと置き換え、その導関数を直接使用します：

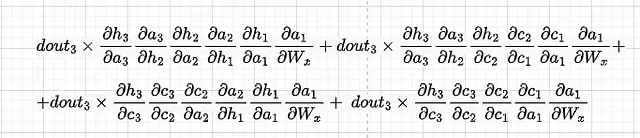
それらを合計すると、dL3/dWxの導関数が得られます。全体の損失に対するdWxの導関数を得るために、dL3/dWxにdL2/dWxとdL1/dWxを加える必要があります。

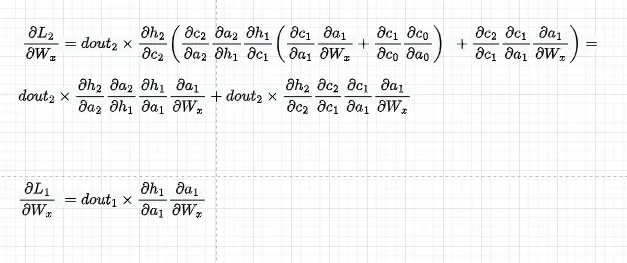
コード:

def lstm_forward(x, h0, Wx, Wh, b, next_c=None):    h, cache = None, None       cache = []    N, T, _ = x.shape    H = h0.shape[-1]    h = np.zeros((N, T, H))    if next_c is None:        next_c = np.zeros((N, H))    for t in range(x.shape[1]):        xt = x[:, t , :]        if t == 0:            next_h, next_c, cache_s = lstm_step_forward(xt, h0, next_c, Wx, Wh, b)            cache.append(cache_s)        else:            next_h, next_c, cache_s = lstm_step_forward(xt, next_h, next_c, Wx, Wh, b)               cache.append(cache_s)            h[:, t, :] = next_h     return h, cachedef dc_da(h, prev_c, next_c_t, i, f, o, g):    dgrad_c = np.zeros((h.shape[0], 4 * h.shape[1]))    dgrad_h = np.zeros((h.shape[0], 4 * h.shape[1]))    # assert dgrad.shape[1] % 4 == 0    H = dgrad.shape[1] // 4        # 2つのフロー（next_hとnext_c）からai、af、ao、agに対する勾配を計算    dnextc_dai = (i * (1-i)) * g    dnextc_daf = (f * (1-f)) * prev_c    dnextc_dao = 0    dnextc_dag = (1 - g**2) * i        dh_dc = o * (1 - next_c_t**2)    dnexth_dai = dh_dc * dnextc_dai    dnexth_daf = dh_dc * dnextc_daf    dnexth_dao = (o * (1-o) * next_c_t)    dnexth_dag = dh_dc * dnextc_dag    # 下流の勾配を便利に計算するために、これらを行列に結合する    dgrad_c[:, 0:H] = dnextc_dai     dgrad_c[:, H:2*H] = dnextc_daf     dgrad_c[:, 2*H:3*H] = dnextc_dao     dgrad_c[:, 3*H:4*H] = dnextc_dag         dgrad_h[:, 0:H] =  dnexth_dai    dgrad_h[:, H:2*H] = dnexth_daf    dgrad_h[:, 2*H:3*H] = dnexth_dao    dgrad_h[:, 3*H:4*H] = dnexth_dag    return dgrad_c, dgrad_hnp.random.seed(1)N, D, T, H = 1, 3, 3, 1x = np.random.randn(N, T, D)h0 = np.random.randn(N, H)Wx = np.random.randn(D, 4 * H)Wh = np.random.randn(H, 4 * H)b = np.random.randn(4 * H)out, cache = lstm_forward(x, h0, Wx, Wh, b)# 単純化のために、doutを定義する代わりに導出するdout = np.random.randn(*out.shape)    # dL3/dWvxdnext_c2 = np.zeros((h0.shape))dnext_h2 = dout[:, -1, :](x2, next_h, prev_h, prev_c, Wx, Wh, next_h, next_c_t2, i2, f2, o2 ,g2) = cache[2]dgrad_c2, dgrad_h2 = dc_da(h0, cache[2][3], cache[2][-5], cache[2][-4],  cache[2][-3], cache[2][-2], cache[2][-1]) dL3_dWx2 = x2.T @ (dgrad_h2 * dnext_h2 + dgrad_c2 * dnext_c2)print(dL3_dWx2)dnext_c1 = dnext_c2 * f2 + dnext_h2 * o2 * (1 - next_c_t2**2) * f2dnext_h1 = (dnext_h2 * dgrad_h2 +  dnext_c2 * dgrad_c2) @ Wh.T(x1, next_h, prev_h, prev_c, Wx, Wh, next_h, next_c_t1, i1, f1, o1 ,g1) = cache[1]dgrad_c1, dgrad_h1 = dc_da(h0, cache[1][3], cache[1][-5], cache[1][-4],  cache[1][-3], cache[1][-2], cache[1][-1])    dL3_dWx1 = x1.T @ (dnext_c1 * dgrad_c1 + dnext_h1 * dgrad_h1)print(dL3_dWx1)dnext_c0 = dnext_c1 * f1 + dnext_h1 * o1 * (1 - next_c_t1**2) * f1dnext_h0 = (dnext_h1 * dgrad_h1 + dnext_c1 * dgrad_c1) @ Wh.T(x0, next_h, prev_h, prev_c, Wx, Wh, next_h, next_c_t0, i0, f0, o0 ,g0) = cache[0]dgrad_c0, dgrad_h0 = dc_da(h0, cache[0][3], cache[0][-5], cache[0][-4],  cache[0][-3], cache[0][-2], cache[0][-1])    dL3_dWx0 = x0.T @ (dnext_c0 * dgrad_c0 + dnext_h0 * dgrad_h0)print(dL3_dWx0)

出力:

[[-0.02349287  0.00135057 -0.11156069 -0.05284914] [ 0.01024921 -0.00058921  0.04867045  0.02305643] [-0.00429567  0.00024695 -0.02039889 -0.00966347]][[-9.83990139e-03  6.78775168e-05 -1.10660923e-03  4.20773125e-04] [ 7.93641636e-03 -5.47469140e-05  8.92540613e-04 -3.39376441e-04] [-2.11067811e-02  1.45598602e-04 -2.37369846e-03  9.02566589e-04]][[-1.95768961e-05  0.00000000e+00  2.77411349e-05 -9.76467796e-03] [ 7.37299593e-06  0.00000000e+00 -1.04477887e-05  3.67754574e-03] [ 6.36561888e-06  0.00000000e+00 -9.02030083e-06  3.17508036e-03]]

losses_dWx = {i : {x_comp : 0 for x_comp in range(i)} for i in range(T)}dWx = np.zeros((D, 4 * H))dWh = np.zeros((H, 4 * H))db = np.zeros((4 * H, ))for idx in range(T-1, -1, -1):    print(f"損失 {idx + 1}")    dnext_c = np.zeros((h0.shape))    dnext_h =  dout[:, idx, :]    for j in range(idx, -1, -1):        (x, next_h, prev_h, prev_c, Wx, Wh, next_h, next_c_t, i, f, o ,g) = cache[j]                dgrad_c, dgrad_h = dc_da(h0, prev_c, next_c_t, i, f, o, g)                 dgrad = dnext_c * dgrad_c + dnext_h * dgrad_h        losses_dWx[idx][j] = x.T @ dgrad                dnext_c = dnext_c * f + dnext_h * o * (1 - next_c_t**2) * f        dnext_h = (dnext_h * dgrad_h +  dnext_c * dgrad_c) @ Wh.T        dnext_h = dgrad @ Wh.T          # 各損失のdWxおよび他のパラメータの勾配を累積する        dWx += x.T @ dgrad        dWh += prev_h.T @ dgrad        db += dgrad.sum(0)        print(f"成分 {j} - ", np.linalg.norm(losses_dWx[idx][j]))

LSTMにおける勾配消失

RNNの場合と同様に、各成分に対する損失L3の勾配を見てみましょう。

損失 3成分 0 - 0.010906688399113558成分 1 - 0.02478099846737857成分 2 - 0.13901933055672275

上記から、L3に最も近いX3が最も大きな更新を持つことがわかりますが、X1とX2はWx1の更新に寄与する量が少ないです。ただし、RNNの場合、この差はより大きくなります。実際、隠れ状態を通過する勾配は、RNNと同様に勾配消失の影響を受けます。たとえば、dL3/dW(x-1)においてWhの項 (dat/dh(t-1)) が依然として現れます。

しかし、入力と隠れ状態に依存するセルを通過する勾配にはWhの項ではなく、シグモイドの項が含まれます（Figure 3の忘却ゲートftの式を参照）。

dct/dc(t-1) = ftということを思い出してください。したがって、忘却ゲートが高い場合、つまり1に近い場合、勾配の消失はバニラRNNよりもはるかに遅い速度で発生しますが、すべての忘却ゲートが正確に1になるわけではないため、それは実際には発生しません。

結論

この記事の主なポイントは、バックプロパゲーションを導出することによって、LSTMは実際には勾配の消失に苦しんでいるが、セル状態のおかげでバニラRNNよりもはるかに低い速度でそれが起こることを理解することでした。これにより、勾配はWxの速度ではなく、忘却ゲートの速度で減衰します。エラーがあれば、コメントで教えてください。

参考文献

• https://web.stanford.edu/class/cs224n/slides/cs224n-2021-lecture06-fancy-rnn.pdf
• http://cs231n.stanford.edu/assignments.html

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!