Rとbrmsを用いた学校卒業者の結果のベイズ比較

Rとbrmsを用いたベイズ比較

ANOVA — ベイズスタイル

学校を卒業した後、私たちが何をしたいのかについては多くの議論があります。私たちは幼い頃から将来何になりたいか尋ねられ、その後13年間を大学前の教育で過ごします。公共政策では、政府、カトリック、独立した学校制度の違いについて、特に非政府学校の公的資金化やリソースの配分方法に関して多くの議論がされています。

学校のセクターによる学生の結果には実際には違いがあるのでしょうか？

オーストラリアのビクトリア州では、州政府が毎年卒業後の結果を評価するための調査を実施しています（On Track Survey）。このデータセット（CC BY 4.0で利用可能）は数年にわたって利用できますが、この記事の執筆時点で最新のものだけを見てみましょう（2021年）。

本記事では、Rパッケージbrmsを使用してベイズ分析手法を適用し、これらの質問に答えることを目指します。

• ユーロトリップの最適化：遺伝的アルゴリズムとGoogle Maps APIによる巡回セールスマン問題の解決
• 「データサイエンスブートキャンプの成功法：完全ガイド」
• ExcelのVBAを使用してプロジェクトの更新トラッカーを作成する

ライブラリとデータセットの読み込み

以下では必要なパッケージを読み込みます。データセットはワイドなレポート形式で提供されており、多くのセルが結合されています。Rはこれが好きではないので、いくつかのハードコーディングを行ってベクトルの名称を変更し、整形されたデータフレームを作成する必要があります。

library(tidyverse) #Tidyverseメタパッケージ
library(brms) #ベイズモデリングパッケージ
library(tidybayes) #ベイズモデルのためのTidyヘルパー関数と可視化ジオメトリ
library(readxl)df <- read_excel("DestinationData2022.xlsx",
sheet = "SCHOOL PUBLICATION TABLE 2022",
skip = 3)colnames(df) <- c('vcaa_code',
'school_name',
'sector',
'locality',
'total_completed_year12',
'on_track_consenters',
'respondants',
'bachelors',
'deferred',
'tafe',
'apprentice_trainee',
'employed',
'looking_for_work',
'other') df <- drop_na(df)

以下はデータセットの一部です。

データセットには14のフィールドがあります。

• VCAAコード — 各コードの管理ID
• 学校名
• セクター — G = 政府、C = カトリック、I = 独立
• 地域または郊外
• 高校卒業生の総数
• On Trackコンセンター
• 応答者
• その他の列は各結果の応答者の割合を表しています

横断的な研究の目的として、セクター別の結果の割合に興味がありますので、このワイドなデータフレームをロング形式に変換する必要があります。

df_long <- df |> mutate(across(5:14, ~ as.numeric(.x)), #数値フィールドを文字列から数値に変換
across(8:14, ~ .x/100 * respondants), #割合から件数を計算
across(8:14, ~ round(.x, 0)), #整数に丸める
respondants = bachelors + deferred + tafe + apprentice_trainee + employed + looking_for_work + other) |> #応答者の合計を再計算
filter(sector != 'A') |> #低ボリューム
select(sector, school_name, 7:14) |> pivot_longer(c(-1, -2, -3), names_to = 'outcome', values_to = 'proportion') |> mutate(proportion = proportion/respondants)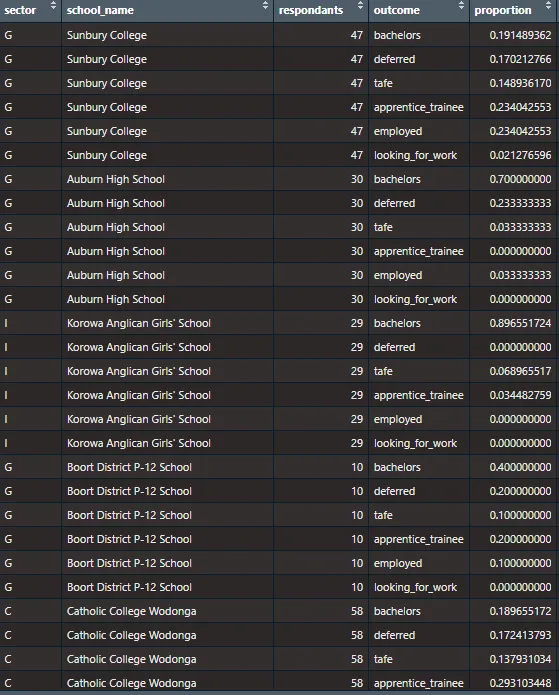

探索的データ分析

データセットを簡単に視覚化して要約しましょう。このデータセットには、政府セクターが157校、独立校が57校、カトリック校が50校がリストされています。

df |>   mutate(sector = fct_infreq(sector)) |>   ggplot(aes(sector)) +    geom_bar(aes(fill = sector)) +     geom_label(aes(label = after_stat(count)), stat = 'count', vjust = 1.5) +    labs(x = 'セクター', y = '数', title = 'セクター別学校数', fill = 'セクター') +    scale_fill_viridis_d(begin = 0.2, end = 0.8) +    theme_ggdist()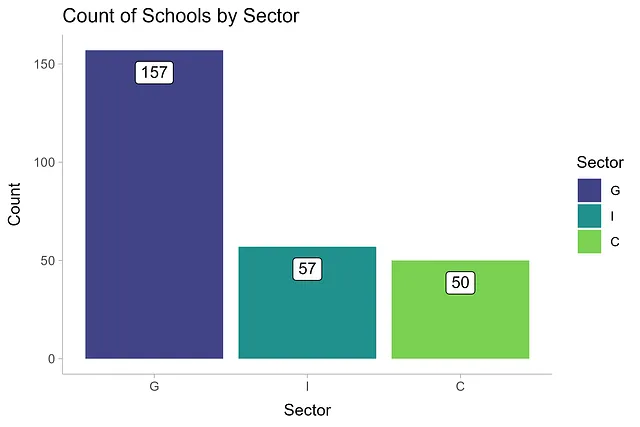

df_long |>   ggplot(aes(sector, proportion, fill = outcome)) +    geom_boxplot(alpha = 0.8) +    geom_point(position = position_dodge(width=0.75), alpha = 0.1, color = 'grey',  aes(group = outcome)) +    labs(x = 'セクター', y = '割合', fill = '結果', title = 'セクターと結果別の割合の箱ひげ図') +    scale_fill_viridis_d(begin = 0.2, end = 0.8) +    theme_ggdist()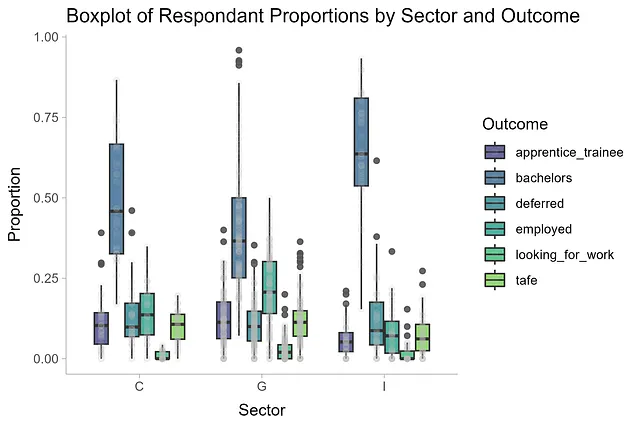

これらの分布は興味深い話をしています。学士の結果は、すべてのセクターにおいて最も変動が大きく、独立校が学部教育を選択する学生の割合の中央値が最も高いことがわかります。高校卒業後の雇用に進む学生の割合の中央値が最も高いのは、政府学校です。その他の結果はあまり変動しませんが、近々再検討します。

統計モデリング — Beta Likelihood Regression

私たちは学校ごとの学生の割合と高校卒業後の結果に焦点を当てています。ベータ尤度はこのような場合に最適です。Buerkner氏による素晴らしいパッケージであるbrmsを使用してベイズモデルを開発します。私たちの目標は、結果とセクターごとの割合の分布をモデル化することです。

ベータ回帰モデルは、μとφの2つのパラメータをモデル化します。μは平均割合を表し、φは精度（または分散）の尺度です。

最初のモデルは以下のように表されます。セクターと結果の間にすでに相互作用があることに注目してください。これはモデルが答えたい質問であり、これはANOVAモデルです。

モデルには、セクターと結果の各組み合わせごとに個別のベータ項を作成するように求めていますが、共通のφ項を持つか、同じ分散で異なる割合平均をモデル化します。これらの割合の50%がロジットスケールで(-3, 1)の間にあるか、割合で(0.01, 0.73)の間にあることを期待しています。これは十分に広いが事前情報をもとにした範囲です。グローバルなPhiの推定値は正の数なので、十分に広いガンマ分布を使用します。

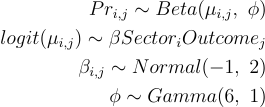
# セクターと結果の相互作用項を使用した割合のモデリング - ベータ - 共通のPhi項m3a <- brm(  proportion ~ sector:outcome + 0,   family = Beta,  data = df_long |> mutate(proportion = proportion + 0.01), # ベータ回帰は0の結果を扱えないため、ここでは微小な増分を追加してずれを修正しています  prior = c(prior(normal(-1, 2), class = 'b'),            prior(gamma(6, 1), class = 'phi')),  iter = 8000, warmup = 1000, cores = 4, chains = 4, seed = 246, save_pars = save_pars(all = T),  control = list(adapt_delta = 0.99, max_treedepth = 15)) |>   add_criterion(c('waic', 'loo'), moment_match = T)summary(m3a)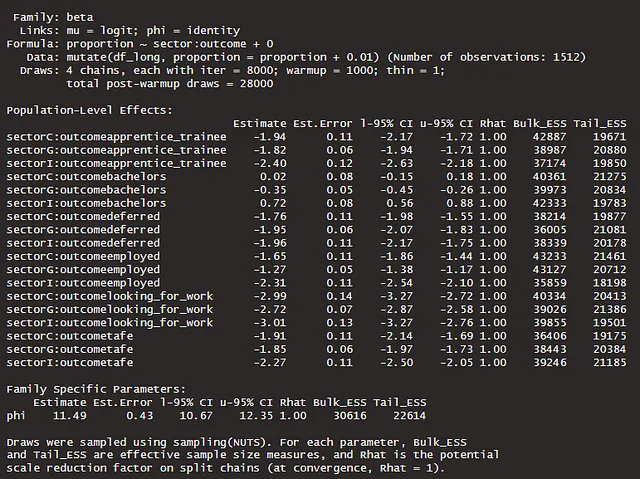

モデルのセットアップでは、すべての比率に1％の増加を追加しました — これはBeta回帰がゼロ値を処理しないためです。 ゼロ膨張ベータを使用してこれをモデル化しようとしましたが、収束には時間がかかりました。

同様に、プールされたphiなしでもモデルを作成できます。これは、上記の分布で観察されたことを考慮すると直感的に理解できます。各セクターとアウトカムの組み合わせにはばらつきがあります。 以下にモデルが定義されています。

m3b <- brm(  bf(proportion ~ sector:outcome + 0,     phi ~ sector:outcome + 0),  family = Beta,  data = df_long |> mutate(proportion = proportion + 0.01),  prior = c(prior(normal(-1, 2), class = 'b')),  iter = 8000, warmup = 1000, cores = 4, chains = 4, seed = 246, save_pars = save_pars(all = T),  control = list(adapt_delta = 0.99)) |>   add_criterion(c('waic', 'loo'), moment_match = T)summary(m3b)

モデル診断と比較

手に入れた2つのモデルを使用して、ベイジアンLOO推定値（elpd_loo）を使用して予測の精度を比較します。

comp <- loo_compare(m3a, m3b)print(comp, simplify = F)

簡単に言えば、期待されるログポイント単位のLOO値が高いほど、未知のデータに対する予測の精度が高くなります。これは、モデル間のモデルの精度の相対的な尺度を提供します。また、観測値とシミュレートされた値の比較による事後予測チェックを行うことで、これをさらに確認できます。私たちの場合、モデルm3bは観測データよりも優れたモデルです。

alt_df <- df_long |>   select(sector, outcome, proportion) |>   rename(value = proportion) |>   mutate(y = 'y',          draw = 99) |>   select(sector, outcome, draw, value, y)sim_df <- expand_grid(sector = c('C', 'I', 'G'),            outcome = unique(df_long$outcome)) |>   add_predicted_draws(m3b, ndraws = 1200) |>   rename(value = .prediction) |>   ungroup() |>   mutate(y = 'y_rep',         draw = rep(seq(from = 1, to = 50, length.out = 50), times = 504)) |>   select(sector, outcome, draw, value, y) |>   bind_rows(alt_df)sim_df |>   ggplot(aes(value, group = draw)) +    geom_density(aes(color = y)) +    facet_grid(outcome ~ sector, scales = 'free_y') +    scale_color_manual(name = '',                        values = c('y' = "darkblue",                                  'y_rep' = "grey")) +    theme_ggdist() +    labs(y = 'Density', x = 'y', title = 'セクターと結果ごとの観測および複製比率の分布')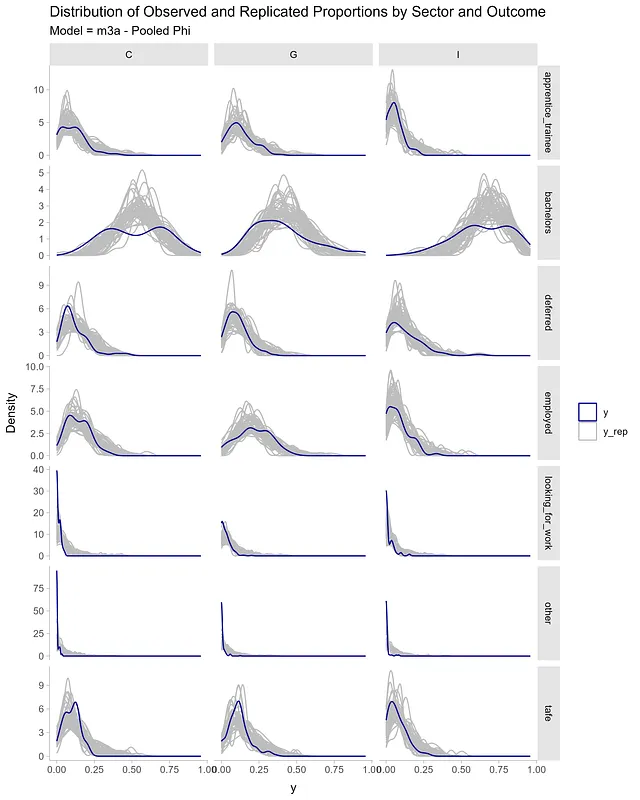

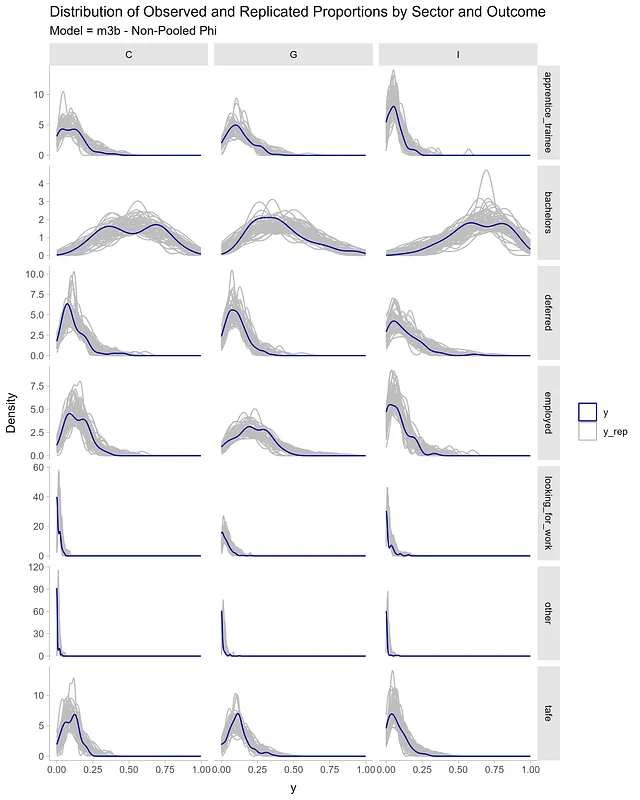
モデルm3bは非プールバリアンスまたはファイ項を持つため、セクターおよび結果ごとの比率分布の変動をより適切に捉えることができます。

ANOVA — ベイズスタイル

思い出してください、私たちの研究の目的は、セクター間やその差がある場合にどのような結果の違いがあるかを理解することです。頻度論的統計では、グループ間の平均値の差のアプローチであるANOVAを使用することがあります。このアプローチの弱点は、結果が推定値と信頼区間を提供するが、これらの推定値に関する不確実性や統計的に有意な平均値の差があるかどうかについての直感的でないp値がないということです。いいえ、お願いしません。

以下では、各セクターと結果の組み合わせに対して予測値のセットを生成し、その後、優れたtidybayes::compare_levels()関数を使用して重要な処理を行います。この関数は、各結果におけるセクター間の事後平均の差を計算します。簡潔さのために、’その他’の結果は除外しました。

new_df <- expand_grid(sector = c('I', 'G', 'C'),           outcome = c('apprentice_trainee', 'bachelors', 'deferred', 'employed', 'looking_for_work', 'tafe'))epred_draws(m3b, newdata = new_df) |>   compare_levels(.epred, by = sector, comparison = rlang::exprs(C - G, I - G, C - I)) |>     mutate(sector = fct_inorder(sector),         sector = fct_shift(sector, -1),          sector = fct_rev(sector))  |>   ggplot(aes(x = .epred, y = sector, fill = sector)) +      stat_halfeye() +      geom_vline(xintercept = 0, lty = 2) +       facet_wrap(~ outcome, scales = 'free_x') +      theme_ggdist() +      theme(legend.position = 'bottom') +      scale_fill_viridis_d(begin = 0.4, end = 0.8) +      labs(x = '比例の差', y = 'セクター', title = 'セクターおよび結果ごとの事後平均の差', fill = 'セクター')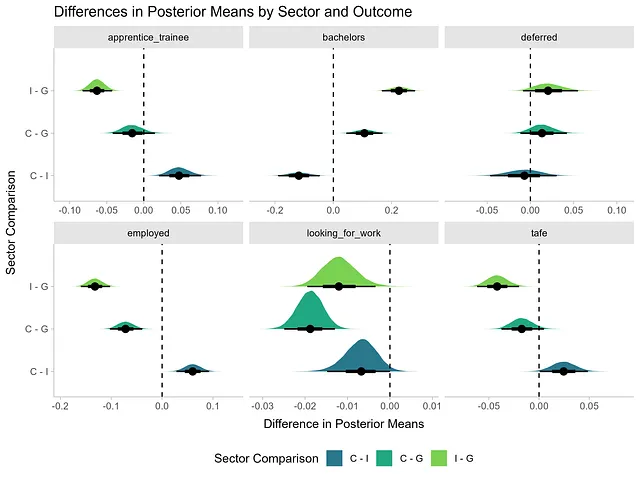

また、これらの分布をより簡単に解釈するために、すべてのセクターと結果の組み合わせについてきれいな表で要約し、89%の信頼区間を表示することもできます。

marg_gt <- epred_draws(m3b, newdata = new_df) |>   compare_levels(.epred, by = sector, comparison = rlang::exprs(C - G, I - G, C - I)) |>   median_qi(.width = .89) |>   mutate(across(where(is.numeric), ~round(.x, 3))) |>   select(-c(.point, .interval, .width)) |>   arrange(outcome, sector) |>   rename(diff_in_means = .epred,          Q5.5 = .lower,          Q94.5 = .upper) |>   group_by(outcome) |>   gt() |>   tab_header(title = 'セクターごとの結果によるマージナル分布') |>   #tab_stubhead(label = 'セクター比較') |>   fmt_percent() |>   gtExtras::gt_theme_pff()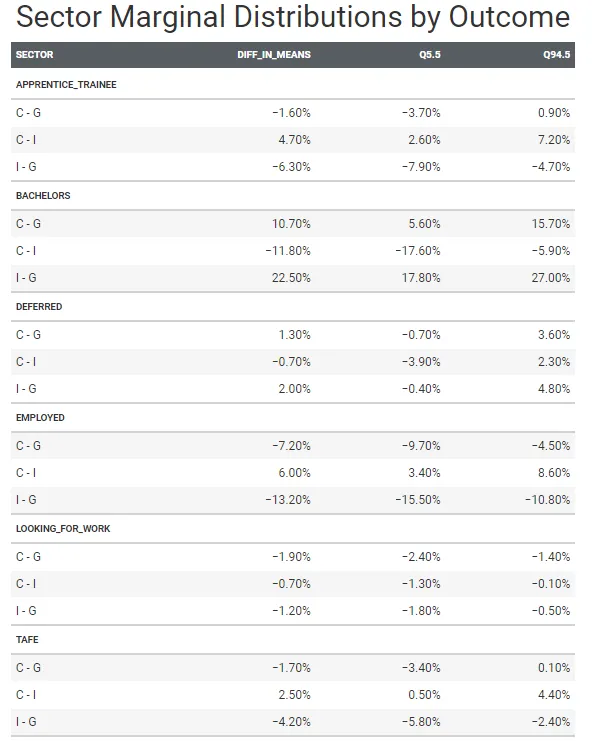

たとえば、公式なレポートで比較を要約する場合、次のように書くことがあります。

政府学校の学生は、VCE修了後に大学の学位を始める可能性がカトリック学校や私立学校の学生よりも低いです。

平均して、政府学校の学生の42.5%（39.5%から45.6%の間）、カトリック学校の学生の53.2%（47.7%から58.4%の間）、私立学校の学生の65%（60.1%から69.7%の間）が、12年生修了後に大学の教育を始めます。

カトリックと政府学生の大学の入学者数の違いは、5.6%から15.7%の間で平均10.7%である確率が89%です。さらに、私立と政府学生の大学の入学者数の違いは、17.8%から27%の間で平均22.5%です。

これらの違いは大きく、これらの違いがゼロでない可能性は100%です。

要約と結論

この記事では、ベイズモデリングを使用してベータ尤度関数を使って比例データをモデル化し、ベイズのANOVAを実行してセクター間の比例的な結果の違いを探索する方法を示しました。

これらの違いの因果関係の理解を作り出すことは目指していません。個々の学生の成績には、社会経済的背景、親の教育達成度、学校レベルでの影響、リソースなど、さまざまな要素が影響していると想像できます。公共政策の非常に複雑な領域であり、しばしばゼロサムの言葉遣いで混乱することがあります。

個人的には、私は家族の中で初めて大学教育に参加し、修了しました。私は中位の公立高校に通い、入学試験でかなり良い点数を取って第一希望校に入学しました。私の両親は教育を追求するように私を奨励し、16歳で学校を辞めることを選びました。この記事は、政府学校と非政府学校の違いが現実であることを示す証拠を提供していますが、本質的には記述的なものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!