「10000 DALL-Eのクレジットでは買えない、Pythonで創った生成アートの方法」

Pythonで生成アートを作る方法は、10000 DALL-Eのクレジットでは買えません

PythonとPillow: DALL-Eができないことをコードする方法

このブログ投稿では、Pythonプログラミング言語を使用して作成したいくつかの生成アートを紹介します。具体的には、PillowとTorchライブラリを利用しています。私の作品のインスピレーションは、オーストリアの音楽作曲家兼ビジュアルアーティスト、Roman Haubenstock-Ramatiの視覚的な構成から得られました。

2021年初頭、自宅のオフィスを飾るためにアートを購入したくてCatawikiを頻繁に閲覧していました。2021年初頭、CatawikiでHaubenstock-Ramatiの創作物に出会ったとき、そのパラメトリックアートの複雑さと美しさにすぐに魅了されました。私は自分のコーディングスキルで何か創造的なことをしたいと思っていたので、同様の出力を生成できるコードを開発することにインスピレーションを受けました。以下の画像は、Roman Haubenstock-Ramatiによって作成された作品の一例です。

Dall-E 2が2022年4月にリリースされた後、モデルを使用してHaubenstock-Ramatiの作品に似たアートを生成することを試みました。モデルにこれを依頼することは議論の余地があります。AIモデルがアーティストの作品に非常に類似した出力を生成できる能力については、オリジナル作品の著作権侵害とみなされる可能性があるという妥当な懸念があります。この議論はこのブログ投稿の範囲外ですが、私がDall-Eに与えたプロンプトは、Haubenstock-Ramatiの作品の正確なコピーを作成することや彼の作品を貶めることを意図していません。私が書いたコードも同様で、彼の作品のコピーを配布することを意図していません。単にPythonを使用して視覚的な幾何学的構成を作成する方法のデモンストレーションです。

• 「今日から使える5つの簡単なPythonの機能で、より良いコードを書き始めることができます」
• 「最高のAIプレゼンテーション生成ツール10選」
• 「倫理的かつ説明可能なAIのための重要なツール」

DALL-Eの出力は興味深いものでしたが、彼のオリジナル作品の本質を完全に捉えることはできませんでした。出力にはHaubenstock-Ramatiのアートに存在する正確な制約と複雑さが欠けていました。さまざまなプロンプトのバリエーションを試しましたが、望んだ結果には近づけませんでした。

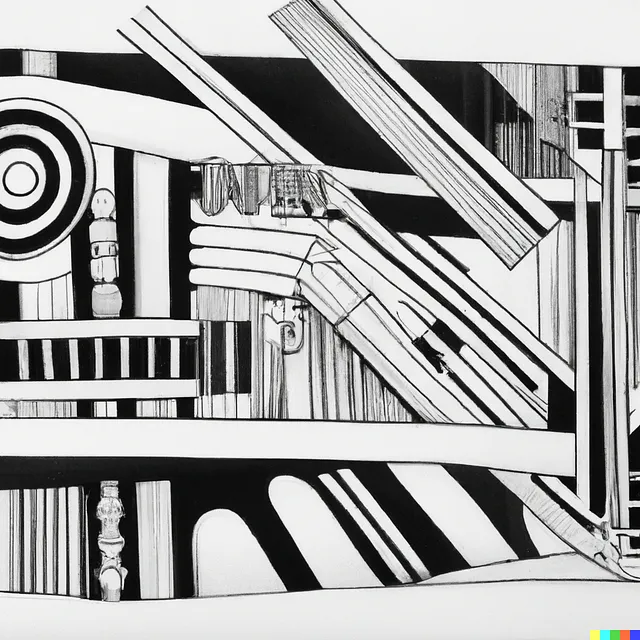
プロセスを簡略化する試みとして、Dall-Eに対して簡単なリクエストを行いました。「縦線を四角形に接続し、四角形に線で正方形を接続し、さらにもう一つの縦線で正方形を別の四角形に接続し、最後に縦線で四角形を円に接続してください」と。驚くべきことに、結果は予想外でした。プロンプトの単純さにもかかわらず、Dall-Eは形状間の意図した関係を理解するのに苦労し、予期しない結果を生み出しました。

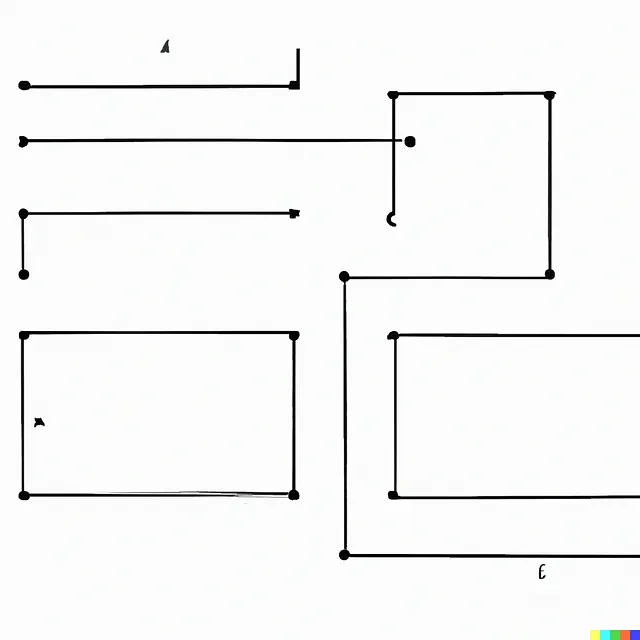
私には明らかになりました、Dall-Eには幾何学的に制約されたプロンプトを処理する能力がないことが、もっと簡単なプロンプトを試してみた結果、「2本の直交する線だけを表示する図を作成してください」というものも難しすぎるということがわかりました。

Dall-Eのこの能力の不足は私にとって驚きでしたが、Dall-Eの仕組みを考えると、それは驚くべきことではありません。Dall-Eは本質的にノイズのある過程であり、制約ベースの正確なプロンプトに最適化されていません。

次に、私が生成した画像を紹介し、このようなコーディング方法について詳しく説明します。

これらの画像はPythonとPillowを使用して作成され、機械学習は一切使用されていません。私のコードによって生成される画像は、Torchを介して導入された要素のランダム性を持っています。Torchは、その使いやすさと便利さのために利用した多目的のパッケージです。通常は機械学習（ML）に使用されるパッケージですが、これらの画像は機械学習（ML）を使用して作成されたものではありません。

画像の多様性がどこから来るのか気になるかもしれませんが、私は個人的に、私のコードが似たような雰囲気を持つが、よく見ると全く異なる画像を生成できることが大好きです。出力の多様性は、重要な特性でした。私のコードが生成する画像の分散は、ランダム変数の緻密な使用によるものです。確率論と統計学の領域では、ランダム変数はランダムな現象の結果として可能な値を取る変数です。

さて、私のコードによって生成された画像の生成プロセスを説明し、この生成プロセスが高レベルの視点からどのように見えるかをいくつかのPythonの例で示します。

生成プロセスは3つのステップに分けることができます。

• ステップ1：中心の部分が生成されます。これは、長方形、線、長方形、正方形、線、円をサンプリングすることによって行われます。これらは固定の位置に配置され、形状のサイズはランダム変数によって決定されます。
• ステップ2：3つのクラスタから、線と隣接するものがサンプリングされます。各クラスタには、さまざまな始点と終点を持つ複数の垂直線が配置されます。
• ステップ3：円と長方形がサンプリングされ、線のクラスタ内に描画されます。

ステップ1

私のコードでランダム変数の役割を理解するために、画像作成プロセスの最初のステップを考えてみましょう：縦長の長方形を形成することです。この長方形は、外見上はシンプルに見えるかもしれませんが、ランダム変数が活動している具体的な体現です。

長方形は、4つの主要な要素に分割できます：開始座標のxとy、および終了座標のxとyです。これらの点は、特定の分布から選択されたときにランダム変数に変換されます。しかし、これらの点の範囲、具体的には、それらがどの分布から来るかをどのように決定するのでしょうか？その答えは、統計学で最も一般的かつ重要な分布の1つである正規分布にあります。

2つのパラメータ（平均（μ）と標準偏差（σ））によって定義される正規分布は、画像生成プロセスにおいて重要な役割を果たします。平均μは分布の中心を示し、ランダム変数の値が集まるポイントとして機能します。標準偏差σは分布のばらつきの度合いを定量化します。これによってランダム変数が取り得る値の範囲が決まります。要するに、より大きな標準偏差は生成される画像の多様性を増大させます。

import torchcanvas_height = 1000canvas_width = 1500#異なる値を表示するためのループfor i in range(5):    #サンプリングするための正規分布の作成    start_y_dist = torch.distributions.Normal(canvas_height * 0.8, canvas_height * 0.05)    #分布からサンプリング    start_y = int(start_y_dist.sample())        #高さをサンプリングするための正規分布の作成    height_dist = torch.distributions.Normal(canvas_height * 0.2, canvas_height * 0.05)    height = int(height_dist.sample())    end_y = start_y + height    #start_xは中央に固定されるため    start_x = canvas_width // 2    width_dist = torch.distributions.Normal(height * 0.5, height * 0.1)    width = int(width_dist.sample())    end_x = start_x + width    print(f"start_x: {start_x}, end_x: {end_x}, start_y: {start_y}, end_y: {end_y}, width: {width}, height: {height}")

start_x: 750, end_x: 942, start_y: 795, end_y: 1101, width: 192, height: 306start_x: 750, end_x: 835, start_y: 838, end_y: 1023, width: 85, height: 185start_x: 750, end_x: 871, start_y: 861, end_y: 1061, width: 121, height: 200start_x: 750, end_x: 863, start_y: 728, end_y: 962, width: 113, height: 234start_x: 750, end_x: 853, start_y: 812, end_y: 986, width: 103, height: 174

正方形のサンプリングは、高さまたは幅のどちらかをサンプリングするだけで非常に似た結果になります。円のサンプリングは、半径のみをサンプリングすればより簡単です。

Pythonで長方形を描画することは、特にPillowライブラリを使用する場合は簡単なプロセスです。以下に、それを行う方法を示します。

from PIL import Image, ImageDraw# 白い背景の新しい画像を作成する# 長方形を描画するためのループfor i in range(5):    img = Image.new('RGB', (canvas_width, canvas_height), 'white')    draw = ImageDraw.Draw(img)    # サンプリングするための正規分布の作成    start_y_dist = torch.distributions.Normal(canvas_height * 0.8, canvas_height * 0.05)    start_y = int(start_y_dist.sample())    height_dist = torch.distributions.Normal(canvas_height * 0.2, canvas_height * 0.05)    height = int(height_dist.sample())    end_y = start_y + height    start_x = canvas_width // 2    width_dist = torch.distributions.Normal(height * 0.5, height * 0.1)    width = int(width_dist.sample())    end_x = start_x + width    # 長方形を描画する    draw.rectangle([(start_x, start_y), (end_x, end_y)], outline='black')    img.show()

ステップ2

これらの画像の垂直線の文脈では、以下の3つのランダム変数を考慮しています:

1. 線の始点のy座標（y_start）
2. 線の終点のy座標（y_end）
3. 線のx座標（x）

垂直線を扱っているため、線ごとにx座標は1つだけサンプリングする必要があります。線の幅は一定であり、キャンバスのサイズで制御されます。

線が交差しないようにするためには、追加の論理が必要でした。簡単さのために、それを無視しましょう。

以下は、Pythonでの例です。

import torchfrom PIL import Image, ImageDraw# キャンバスのサイズを設定するcanvas_size = 1000# 線の数num_lines = 10# 始点と終点のy座標、およびx座標の分布を作成するy_start_distribution = torch.distributions.Normal(canvas_size / 2, canvas_size / 4)y_end_distribution = torch.distributions.Normal(canvas_size / 2, canvas_size / 4)x_distribution = torch.distributions.Normal(canvas_size / 2, canvas_size / 4)# 各線に対して分布からサンプリングするy_start_points = y_start_distribution.sample((num_lines,))y_end_points = y_end_distribution.sample((num_lines,))x_points = x_distribution.sample((num_lines,))# 白いキャンバスを作成するimage = Image.new('RGB', (canvas_size, canvas_size), 'white')draw = ImageDraw.Draw(image)# 線を描画するfor i in range(num_lines):    draw.line([(x_points[i], y_start_points[i]), (x_points[i], y_end_points[i])], fill='black')# 画像を表示するimage.show()

ただし、これによって行のみが得られます。クラスタのもう一部分は、行の末尾にある円、これを隣接する円と呼びます。ランダム変数もそのプロセスを決定します。まず、隣接する円が存在するかどうかはベルヌーイ分布からサンプリングされ、形状の位置（左、中央、右）は一様分布からサンプリングされます。

円は半径という単一のパラメータで完全に定義することができます。行の長さを円の半径に影響を与える条件と考えることができます。これにより、円の半径（R）が行の長さ（L）に依存する条件付き確率モデルが形成されます。条件付きガウス分布を使用します。この分布の平均（μ）は行の長さの平方根の関数であり、標準偏差（σ）は定数です。

最初に、行の長さLが与えられた場合、半径Rは正規分布に従うと仮定します。これはR | L ~ N(μ(L), σ²)と表されます。ここで、Nは正規（ガウス）分布を意味し、σは標準偏差です。

しかし、これには小さな問題があります。正規分布には負の値をサンプリングする可能性が含まれています。この結果は物理的には不可能であり、半径は負になることはありません。

この問題を回避するために、半正規分布を使用することができます。この分布は正規分布と同様にスケールパラメータσによって定義されますが、重要なのは非負の値に制約されていることです。行の長さが与えられた場合、半径は半正規分布に従います：R | L ~ HN(σ)、ここでHNは半正規分布を示します。これにより、すべてのサンプルされた半径が非負であり、分布の平均が√(2L)であることを保証するために、σは希望する平均によってσ = √(2L) / √(2/π)と決定されます。

from PIL import Image, ImageDraw
import numpy as np
import torch

# 定義する行の長さL
L = 3000

# 半正規分布のための希望する平均を計算する
mu = np.sqrt(L * 2)

# 平均を与えるためのスケールパラメータを計算する
scale = mu / np.sqrt(2 / np.pi)

# 計算したスケールパラメータで半正規分布を作成する
dist = torch.distributions.HalfNormal(scale / 3)

# 複数の円をサンプリングして描画する
for _ in range(10):
    # 白い背景の新しいイメージを作成する
    img_size = (2000, 2000)
    img = Image.new('RGB', img_size, (255, 255, 255))
    draw = ImageDraw.Draw(img)

    # 円の中心を定義する
    start_x = img_size[0] // 2
    start_y = img_size[1] // 2

    # 分布から半径をサンプリングする
    r = int(dist.sample())
    print(f"サンプリングされた半径：{r}")

    # 円の境界ボックスを定義する
    bbox = [start_x - r, start_y - r, start_x + r, start_y + r]

    # イメージに円を描画する
    draw.ellipse(bbox, outline ='black', fill=(0, 0, 0))

    # イメージを表示する
    img.show()

ステップ3

ステップ3では、ステップ1とステップ2の要素を組み合わせます。ステップ1では、固定された位置に矩形をサンプリングして描画するタスクに取り組みました。ステップ2では、正規分布を使用してキャンバスの一部に直線を描画する方法を学びました。さらに、円をサンプリングして描画する方法についても学びました。

ステップ3に移行するにあたり、前のステップからの技術を再利用します。目標は、前にサンプリングした直線の周りに正方形と円を調和して配置することです。このタスクには再び正規分布が役立ちます。

直線のクラスタを作成するために使用したパラメータを再利用します。ただし、視覚的な魅力を高め、重なりを避けるために、平均（mu）と標準偏差の値にいくらかのノイズを導入します。

このステップでは、直線を配置する代わりにサンプルされた矩形と円を配置することが私たちのタスクです。これらの技術を試してみて、直線のクラスタに円や矩形を追加できるかどうかを試してみることをお勧めします。

このブログ投稿では、コードの基礎を解析して簡素化することで、その動作の深い理解を可能にしました。Dall-Eのような生成AIモデルが正確な制約に従うのは困難であることを示しました。

これらの画像を生成するためのコードを書くことは、私にとって素晴らしい経験でした。コードの1行ごとに画像が進化していくのを見るのはとても面白かったです。このブログ投稿が、アートとコーディングの交差点に興味を持っていただけたら嬉しいです。コーディングのスキルを使って想像力をコードで具現化してみてください。Dall-Eのクレジットを使い果たす必要はありません。創造の力はすぐそこにあります。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!