Pythonを使用して地理的な巡回セールスマン問題を解決する

Pythonで巡回セールスマン問題を解決する

pyconcordeを使用して実世界の経路問題の最適解を見つける

有名な巡回セールスマン問題（TSP）は、ノード（都市）の集合間の最適な経路を見つけ、出発地に戻ることに関するものです。簡単なように聞こえますが、ノードの数が多い場合には、n個の都市の順序の可能性の数はn!となり、これはたとえばわずか30の都市でも、チェックする必要がある旅行の数が265,252,859,812,191,058,636,308,480,000,000になることを意味します。大規模なTSPの問題は、パワフルなコンピュータでも、力ずくで解くことは現実的ではありません。

幸いにも、大規模なTSPを解くために計算が必要な量を劇的に減らすアルゴリズムがいくつか開発されています。そのようなソフトウェアの1つであるConcordeは、数十年前に学術界で使用するために開発されました。独立したソフトウェアとして使用するにはかなり技術的なものであり、専門家のみを対象としていますが、ConcordeのPythonラッパーであるpyconcordeが開発されました。Concordeで使用されるアルゴリズムの説明は、この記事の範囲外です。ただし、Pythonでこれらの問題とその解決策を再現するために必要なコードについては説明します。

実世界の地理的なTSP

実世界の地理的な巡回セールスマン問題を解決する方法はどのようなものでしょうか？実世界のポイントは上記の画像のような単純な2Dの線で接続されているわけではありません。代わりに、地理的な特徴はさまざまな可能な経路で接続され、その経路は歩行、自転車、自動車運転などに応じて変化します。

データサイエンティストやソフトウェアエンジニアが実世界のTSPを解決したい理由は、次のような使用例のいくつかです：

• 新しいAI研究がGPT4RoIを紹介します：地域テキストペアに基づくInstruction Tuning大規模言語モデル（LLM）によるビジョン言語モデル
• ペンシルバニア大学の研究者は、RNNベースのリザーバーコンピュータを設計およびプログラムするための代替AIアプローチを紹介しました
• 研究者たちは、ナノLEDの正確なアレイを育成しました

1. クーリエを雇用している会社は、各ドライバーの道路での時間を最小限に抑える都市内の最適なルートの計算方法が必要です。
2. ツアーオペレーターは、所定の時間内に一連の目的地を最短経路で接続する方法を見つける必要があります。
3. 廃棄物処理会社や地方自治体は、ピックアップができるだけ効率的に順序付けられるようにリソースを割り当てる必要があります。

実世界のTSPを解決するためには、routingpyライブラリを使用して、[経度、緯度]の地理的なポイント間の経路、距離（メートル単位）、時間（秒単位）を見つけることができます。この記事では、そのような問題に使用できる方法について説明します。

コーディングの手順

Pythonを使用して地理的なTSPを解決するためのガイドラインがここに概説されています。問題解決プロセスの大まかな構造は次の通りです：

1. [経度、緯度]のペアとしてn個の座標のリストを取得します。
2. ルーティングサービスを使用して、各座標間の実世界の所要時間の行列（n x n）を取得します。この行列は非対称です（AからBへの運転はBからAへの正確な逆ではありません）。
3. （n x n）行列を対称行列（2n x 2n）に変換します。
4. この行列をConcordeソルバーに供給して、座標の最適な順序を見つけます。
5. ルーティングサービスを使用して実世界の経路を作成します。
6. 結果を地図上で視覚化します。
7. オプションで最終経路のGPXファイルを作成します。

これらの手順は詳細に説明されます。

ステップ1：座標の取得

この例では、イギリスの79の都市間で車を運転する問題を考えます。以下にイギリスの都市の地図が青で表示されています。データサイエンティストは、さまざまな方法で座標を見つけることができます。必要に応じて、GoogleマップやGoogle Earthを使用して手動で見つけることもできます。

この例で使用されるコード構造とデータは、このGitHubリポジトリでも利用できます。

以下に、都市の座標を含むCSVファイル（リポジトリ内のgb_cities.csv）と、pandasを使用してそれをインポートするために必要なコードが示されています。

Place Name,Latitude,LongitudeAberdeen,57.149651,-2.099075Ayr,55.458565,-4.629179Basildon,51.572376,0.470009Bath,51.380001,-2.36Bedford,52.136436,-0.460739...

import pandas as pddf = pd.read_csv('gb_cities.csv')coordinates = df[['Longitude', 'Latitude']].valuesnames = df['Place Name'].values

ステップ2：ルーティングサービスを使用して所要時間行列を取得する

routingpyライブラリを介して利用可能な数多くのルーティングサービスがあります。GraphhopperのAPIには無料の利用枠があり、制限付きで使用することができます。routingpyを介して利用可能な他のルーターについてはドキュメントを参照してください。

import routingpy as rpimport numpy as npapi_key = # https://www.graphhopper.com/apiで無料のキーを取得します。api = rp.Graphhopper(api_key=api_key)matrix = api.matrix(locations=coordinates, profile='car')durations = np.matrix(matrix.durations)print(durations)

ここには、座標間のドライブ時間の79 x 79行列であるdurationsがあります：

matrix([[    0, 10902, 30375, ..., 23380, 25233, 19845],        [10901,     0, 23625, ..., 16458, 18312, 13095],        [30329, 23543,     0, ...,  8835,  9441, 12260],        ...,        [23397, 16446,  9007, ...,     0,  2789,  7924],        [25275, 18324,  9654, ...,  2857,     0,  9625],        [19857, 13071, 12340, ...,  8002,  9632,     0]])

都市間のドライブ時間は次のように決定できます：

1. 各行と列は都市に対応しています。アバディーンは最初の行と列、エアは2番目、バジルドンは3番目、以降です。
2. アバディーンからエアまでの時間を求めるには、1行目の2列目を見てください：10,902秒です。逆の時間（エアからアバディーンへ）は10,901秒です。
3. 一般的に、i番目の都市からj番目の都市への時間は、i番目の行とj番目の列の交差点にあります。

予想通り、行列には対角線上にゼロがあります。各ポイントは自分自身との距離または所要時間がゼロで結ばれています。また、行列は完全に対称ではありません。都市間のドライブ時間は、道路のレイアウトや交通の渋滞箇所が異なるため、逆方向では同一ではない可能性があります。ただし、おおよそ似ています。

ステップ3：非対称行列を対称行列に変換する

pyconcordeで最適な順序を生成するためにこの行列を使用する前に、行列を対称化する必要があります。非対称なTSPを対称なTSPに変換するための手法については、JonkerおよびVolgenant（1983）の論文「Transforming asymmetric into symmetric traveling salesman problems, Operations Research Letters, 2(4), 161–163」で説明されています。以下に、この変換の理論が続きます。必要な場合は、このセクションをスキップして地理的な非対称TSPを対称化するセクションまでスクロールしてください。

ジョンカー/ボルゲナント非対称から対称への変換

以下は3つのノードを持つ非対称TSPの可視化とその距離行列です。

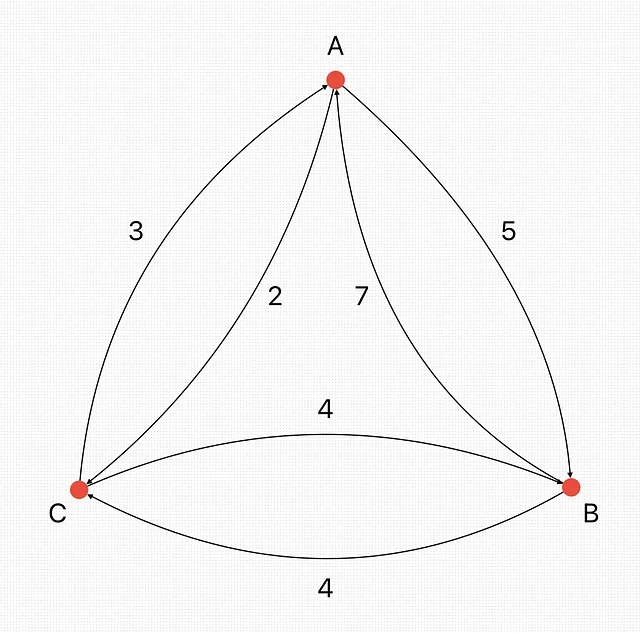
matrix([[0, 5, 2],        [7, 0, 4],        [3, 4, 0]])

以下はこの非対称TSPを対称TSPに変換するために使用される方法のスケッチです。

1. 新しいゴーストノードA’、B’、C’を作成します。AをA’、BをB’、CをC’と距離ゼロで接続します。
2. ノードを以下のように重みで接続します。AからBはA’からBに、BからAはB’からAになります。BからCはB’からCに、CからBはC’からBになります。CからAはC’からAに、AからCはA’からCになります。
3. 他のすべてのエッジの重みを無限大に設定し、アルゴリズムがそれらの間を移動しようとしないようにします。ただし、後でpyconcordeを使用する際には実用的ではないため、他の重みを最高の重みよりもはるかに高く設定します。この場合、99とします。

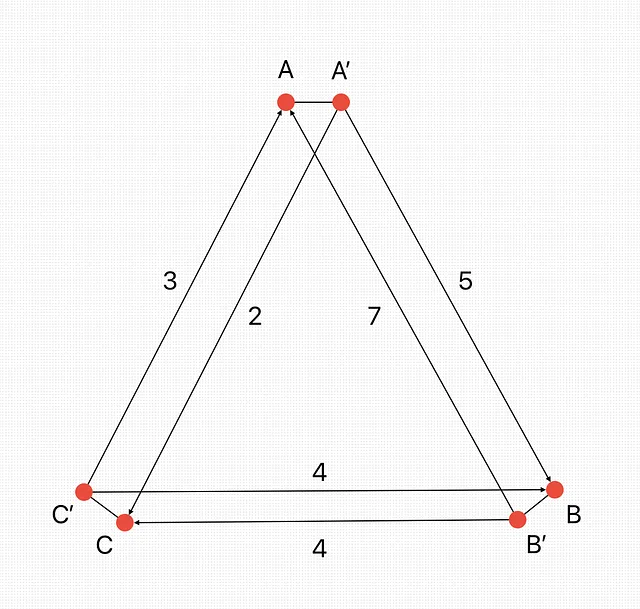
以下は結果の距離行列です。行列内のノードの順序は、A、B、C、A’、B’、C’です。

matrix([[ 0, 99, 99,  0,  7,  3],        [99,  0, 99,  5,  0,  4],        [99, 99,  0,  2,  4,  0],        [ 0,  5,  2,  0, 99, 99],        [ 7,  0,  4, 99,  0, 99],        [ 3,  4,  0, 99, 99,  0]])

対角線はゼロであり、行列は現在対称です。元の行列は、新しい行列の左下隅にあり、その転置は右上にあります。同時に、左上と右下の部分にはノード間の非常に高い重みが含まれています。

A、B、C（左上）はもはや互いに接続されていません（厳密には、実用上の目的のために無限の代わりに非常に高い重みで接続されています）。これは、どのアルゴリズムもこれらのノード間のパスを見つけようとしないことを意味します。同様に、A’、B’、C’（右下）も互いに接続されていません。代わりに、元の非対称ネットワークの方向性は、元のノードA、B、CとそのゴーストA’、B’、C’の重みによってここで表されます。

元の非対称問題の解と新しい対称TSPの解との間には一対一の対応関係があります：

• A — B — C — AはA — A’ — B — B’ — C — C’ — Aに対応します
• A — C — B — AはA — A’ — C — C’ — B — B’ — Aに対応します

それぞれの場合、ゴーストノードA’、B’、C’は元のノードA、B、Cと交互に配置され、各元のノードはその「パートナー」ゴーストノード（AはA’に隣接しているなど）に隣接しています。

地理的非対称TSPの変換

実用的な例に戻ります。非対称TSP行列を対称な行列に変換する関数を作成できます：

def symmetricize(m, high_int=None):        # high_intが指定されていない場合、最大値の10倍にします。    if high_int is None:        high_int = round(10*m.max())            m_bar = m.copy()    np.fill_diagonal(m_bar, 0)    u = np.matrix(np.ones(m.shape) * high_int)    np.fill_diagonal(u, 0)    m_symm_top = np.concatenate((u, np.transpose(m_bar)), axis=1)    m_symm_bottom = np.concatenate((m_bar, u), axis=1)    m_symm = np.concatenate((m_symm_top, m_symm_bottom), axis=0)        return m_symm.astype(int) # Concordeは整数の重みを必要とします

symmetricize(durations) は次の値を返します：

matrix([[     0, 461120, 461120, ...,  23397,  25275,  19857],        [461120,      0, 461120, ...,  16446,  18324,  13071],        [461120, 461120,      0, ...,   9007,   9654,  12340],        ...,        [ 23397,  16446,   9007, ...,      0, 461120, 461120],        [ 25275,  18324,   9654, ..., 461120,      0, 461120],        [ 19857,  13071,  12340, ..., 461120, 461120,      0]])

この 158 x 158 の行列には、durations のコピーが左下にあり、転置されたコピーが右上にあります。461,120 の高い値（durations の最大値の10倍）は、実際の目的においてはこの期間を持つノードが接続されていないことを意味します。

この行列は最適なパスを計算するために最終的に pyconcorde に供給されます。

ステップ4：Concordeソルバーの使用

pyconcordeのインストール

次のコマンドを実行してpyconcordeをインストールします（インストールはLinuxまたはMac OSで利用可能ですが、現在はWindowsでは利用できません）：

virtualenv venv                                  # 仮想環境を作成source venv/bin/activate                         # 仮想環境をアクティブ化git clone https://github.com/jvkersch/pyconcorde # gitリポジトリをクローンcd pyconcorde                                    # ディレクトリを移動pip install -e .                                 # pyconcordeをインストール

PythonでTSPを解く

これで、Pythonスクリプトでconcordeからインポートできます。

from concorde.problem import Problemfrom concorde.concorde import Concordedef solve_concorde(matrix):    problem = Problem.from_matrix(matrix)    solver = Concorde()    solution = solver.solve(problem)    print(f'Optimal tour: {solution.tour}')    return solution

対称的な期間の行列はsolve_concorde()に供給することができます。

durations_symm = symmetricize(durations)solution = solve_concorde(durations_symm)

以下はプリント出力です：

Optimal tour: [0, 79, 22, 101, 25, 104, 48, 127, 68, 147, 23, 102, 58, 137, 7, 86, 39, 118, 73, 152, 78, 157, 36, 115, 42, 121, 62, 141, 16, 95, 20, 99, 51, 130, 40, 119, 19, 98, 59, 138, 50, 129, 54, 133, 27, 106, 10, 89, 4, 83, 66, 145, 33, 112, 14, 93, 2, 81, 45, 124, 32, 111, 11, 90, 29, 108, 34, 113, 24, 103, 8, 87, 17, 96, 56, 135, 64, 143, 61, 140, 75, 154, 52, 131, 71, 150, 18, 97, 3, 82, 9, 88, 74, 153, 55, 134, 72, 151, 28, 107, 12, 91, 70, 149, 65, 144, 35, 114, 31, 110, 77, 156, 63, 142, 41, 120, 69, 148, 6, 85, 76, 155, 67, 146, 15, 94, 44, 123, 47, 126, 60, 139, 57, 136, 38, 117, 13, 92, 5, 84, 43, 122, 49, 128, 46, 125, 21, 100, 1, 80, 30, 109, 53, 132, 37, 116, 26, 105]

このソリューションでは、最適なツアーのノードの順序が示されています。このソリューションには、元のノード（0から78までの番号が付けられたノード）とそのパートナーゴーストノード（79から157）が交互に含まれていることに注意してください：

• 0は79とパートナーシップを組んでいます。
• 22は101とパートナーシップを組んでいます。
• 25は104とパートナーシップを組んでいます。など。

これは、ソリューションが正しく機能していることを示しています。

ステップ5：実世界のルートの作成

次のステップは、ソリューションの交互の要素（元の79の都市に対応するノード）を選び、それに応じて座標を順序付けることです。

# 交互の要素を選ぶ：これらは元のツアーに対応しますstour = solution.tour[::2]# 元の座標と名前を順序付けるcoords_ordered = [coordinates[i].tolist() for i in tour]names_ordered = [names[i] for i in tour]

names_orderedの最初の数つの都市名は次のとおりです（最適なツアーの都市の実際の順序）：

['アバディーン'、 'ダンディー'、 'エジンバラ'、 'ニューカッスル・アポン・タイン'、 'サンダーランド'、 'ダラム'、 ...]

最後に、最初の都市を戻して完全なループツアーを作成し、最終的なルートをGraphhopperの方向APIを使用して取得します。

# 完全なループのために最初の都市を追加するcoords_ordered_return = coords_ordered + [coords_ordered[0]]# 順序付けられたループの完全な運転手の指示を取得するための方向api.directions(locations=coords_ordered_return, profile='car')

ステップ6：マップ上での可視化

マップ上で最終的なルートを表示することで、結果に自信を持つことができるだけでなく、実用的な設定でソリューションを使用することもできます。次のコードは、HTMLに保存できるfoliumマップを表示します。

import foliumdef generate_map(coordinates, names, directions):    # foliumは緯度、経度が必要です    coordinates = [(y、x) for (x、y) in coordinates]    route_points = [(y、x) for (x、y) in directions.geometry]    lat_centre = np.mean([x for (x、y) in coordinates])    lon_centre = np.mean([y for (x、y) in coordinates])    centre = lat_centre、lon_centre    m = folium.Map(location=centre、zoom_start=1、zoom_control=False)    # ルートの線をプロットする    folium.PolyLine(route_points、color='red'、weight=2).add_to(m)        # 各ポイントをホバーのツールチップでプロットする      for i、(point、name) in enumerate(zip(coordinates、names)):        folium.CircleMarker(location=point、                      tooltip=f'{i}：{name}'、                      radius=2).add_to(m)    custom_tile_layer = folium.TileLayer(        tiles='http://{s}.basemaps.cartocdn.com/light_all/{z}/{x}/{y}.png'、        attr='CartoDB Positron'、        name='Positron'、        overlay=True、        control=True、        opacity=0.7  # グレーアウトのレベルを調整するために不透明度を調整する    )    custom_tile_layer.add_to(m)    folium.LayerControl().add_to(m)    sw = (np.min([x for (x、y) in coordinates])、np.min([y for (x、y) in coordinates]))    ne = (np.max([x for (x、y) in coordinates])、np.max([y for (x、y) in coordinates]))    m.fit_bounds([sw、ne])    return mgenerate_map(coords_ordered、names_ordered、directions).save('gb_cities.html')

結果はこの記事の上部に表示されています。ここをクリックしてインタラクティブなマップとして表示します。マップをズームインして詳細を表示し、個々の都市にホバーすると、ツアーのシーケンス番号が表示されます。以下は、最適なツアー上のリンカーンとチェスターフィールドの間を通るルートを示すマップの一部を拡大表示したものです。

ステップ7：オプション：GPXファイルの作成

計算された経路を実際にたどる必要がある場合、例えばGPS搭載のデバイス（携帯電話やカーナビゲーションシステムなど）で、GPXファイルを作成することができます。これは最適化問題の一部ではありませんが、経路をファイルに保存したい場合に利用できるオプションの追加ステップです。GPXファイルはdirections変数から作成されます：

def generate_gpx_file(directions, filename):    gpx_template = """<?xml version="1.0" encoding="UTF-8"?>    <gpx version="1.1" xmlns="http://www.topografix.com/GPX/1/1"        xmlns:xsi="http://www.w3.org/2001/XMLSchema-instance"        xsi:schemaLocation="http://www.topografix.com/GPX/1/1        http://www.topografix.com/GPX/1/1/gpx.xsd">        <trk>            <name>Track</name>            <trkseg>{}</trkseg>        </trk>    </gpx>    """    trkseg_template = """        <trkpt lat="{}" lon="{}"/>    """    trkseg_elements = ""    for point in directions.geometry:        trkseg_elements += trkseg_template.format(point[1], point[0])    gpx_data = gpx_template.format(trkseg_elements)    with open(filename, 'w') as file:        file.write(gpx_data)generate_gpx_file(directions, 'gb_cities.gpx')

この問題のGPXファイルはこちらからダウンロードできます。

結論

実世界の地理的な巡回セールスマン問題を解決するために、以下の要素を組み合わせる方法を見てきました：

1. routingpyライブラリからの方向と所要時間の行列。適切なprofile（交通手段）を指定します。
2. pyconcordeラッパーを介した効率的かつ強力なConcordeソルバーを使用して、最適な経路を提供します。
3. 地図を作成するためのfoliumを使用した可視化。

上記のドライブツアーは、79都市の巡回セールスマン問題に対する説得力のある解決策であり、Concordeソルバーによれば証明された「最適」です。ただし、実世界のデータを扱っているため、最終結果は入力に依存します。routingpyから得られる地点間所要時間の行列が実世界を適切に表していることを期待しています。実際には、地点間の徒歩、自転車、または車での所要時間は、時間帯や曜日によって異なります。これは使用した方法の制限です。最終結果に対してより自信を持つ方法の1つは、同じ方法を別のルーティングサービスで試すことです。各ルーティングサービス（Graphhopper、ORS、Valhallaなど）は、ここで説明したようなTSP問題に使用できる独自のAPIを持っており、さまざまなサービスの結果を比較することができます。

このような問題を解決する方法の現実世界の制限にもかかわらず、上記の手法は、できるだけ効率的に都市内を移動する必要がある営業担当者や配達員、または観光客が可能な限り多くの観光名所を巡るための良い出発点を提供します。結果をインタラクティブな地図上で視覚化し、ルートをGPXファイルとして保存することで、解決策はデータサイエンティストだけでなく、最終ユーザーにとっても有用です。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!