タイムシリーズ分析：PythonにおけるARIMAモデル

PythonでのARIMAモデルによるタイムシリーズ分析

時間系列分析は、時間系列の将来のポイントを予測するために広く使用されています。AutoRegressive Integrated Moving Average（ARIMA）モデルは、時間系列予測に広く使用され、最も人気のある手法の1つとされています。このチュートリアルでは、Pythonでの時間系列予測のためのARIMAモデルの構築と評価方法を学びます。

 

ARIMAモデルとは何ですか？

 

ARIMAモデルは、時間系列データの分析と予測に使用される統計モデルです。ARIMAアプローチは、時間系列で見られる標準的な構造に明示的に対応し、優れた時間系列予測を行うためのシンプルでパワフルな方法を提供します。

• 「MetaGPTと出会ってください：GPTをエンジニア、建築家、マネージャに変えるオープンソースAIフレームワーク」
• マルチモーダル医療AI
• 「AnyLocによる最新のビジュアル位置認識（VPR）の汎用方法について紹介します」

ARIMAは、AutoRegressive Integrated Moving Averageの略で、次の3つの要素を組み合わせています：

• 自己回帰（AR）：現在の観測値と過去の観測値との相関を利用するモデルです。過去の観測値の数は、ラグオーダーまたはpと呼ばれます。
• 積分（I）：生の観測値の差分を取ることで、時間系列を定常にします。差分の回数は、dと呼ばれます。
• 移動平均（MA）：現在の観測値と過去の観測値に適用された移動平均モデルの残差との関係を考慮します。移動平均窓のサイズは、オーダーまたはqと呼ばれます。

ARIMAモデルは、使用される具体的なモデルを指定するために整数値で置き換えられる記号ARIMA(p,d,q)で定義されます。

ARIMAモデルを採用する際の主な仮定：

• 時間系列は、基になるARIMAプロセスから生成されたものです。
• パラメータp、d、qは、生の観測値に基づいて適切に指定する必要があります。
• ARIMAモデルを適合させる前に、時間系列データを差分化して定常にする必要があります。
• モデルが適切に適合している場合、残差は無相関であり、正規分布に従うはずです。

要約すると、ARIMAモデルは、予測などの目的で時間系列データをモデリングするための構造化された設定可能な手法を提供します。次に、PythonでARIMAモデルを適合させる方法について見ていきます。

 

Pythonコードの例

 

このチュートリアルでは、KaggleからNetflixの株価データを使用して、ARIMAモデルを使用してNetflixの株価を予測します。 

 

データの読み込み

 

株価データセットを「日付」列をインデックスとして読み込みます。 

import pandas as pd


net_df = pd.read_csv("Netflix_stock_history.csv", index_col="Date", parse_dates=True)
net_df.head(3)

 

 

データの可視化

 

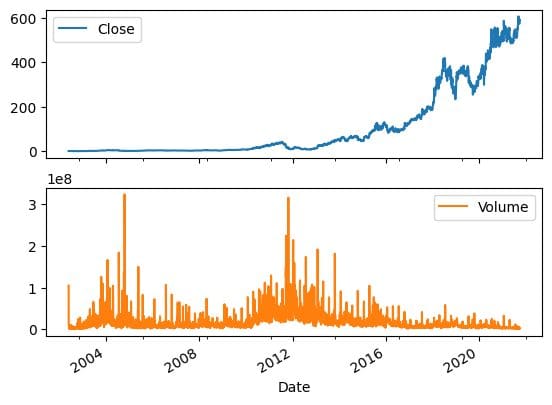
pandasの「plot」関数を使用して、株価と出来高の変化を時間の経過とともに可視化することができます。株価は指数関数的に増加していることがわかります。

net_df[["Close","Volume"]].plot(subplots=True, layout=(2,1));

 

 

ローリング予測ARIMAモデル

 

データセットはトレーニングセットとテストセットに分割され、ARIMAモデルをトレーニングしました。最初の予測が行われました。

一般的なARIMAモデルでは結果が悪く、フラットな線が生成されました。そのため、ローリング予測法を試すことにしました。 

注：コードの例はBOGDAN IVANYUKのノートブックの改変版です。

from statsmodels.tsa.arima.model import ARIMA
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math


train_data, test_data = net_df[0:int(len(net_df)*0.9)], net_df[int(len(net_df)*0.9):]


train_arima = train_data['Open']
test_arima = test_data['Open']


history = [x for x in train_arima]
y = test_arima
# make first prediction
predictions = list()
model = ARIMA(history, order=(1,1,0))
model_fit = model.fit()
yhat = model_fit.forecast()[0]
predictions.append(yhat)
history.append(y[0])

 

時間系列データを扱う際には、前の観測値に依存するため、ローリング予測がよく必要になります。これを行う一つの方法は、新しい観測値が受け取られるたびにモデルを再作成することです。

すべての観測値を追跡するために、historyというリストを手動で保持し、最初にトレーニングデータが含まれ、各反復ごとに新しい観測値が追加されます。このアプローチは、正確な予測モデルを得るのに役立ちます。

# ローリング予測
for i in range(1, len(y)):
    # 予測
    model = ARIMA(history, order=(1,1,0))
    model_fit = model.fit()
    yhat = model_fit.forecast()[0]
    # 逆変換された予測
    predictions.append(yhat)
    # 観測値
    obs = y[i]
    history.append(obs)

 

モデルの評価

 

ローリング予測ARIMAモデルは、シンプルな実装に比べて100%の改善を示し、印象的な結果をもたらしました。

# パフォーマンスレポート
mse = mean_squared_error(y, predictions)
print('MSE: '+str(mse))
mae = mean_absolute_error(y, predictions)
print('MAE: '+str(mae))
rmse = math.sqrt(mean_squared_error(y, predictions))
print('RMSE: '+str(rmse))

 

MSE: 116.89611817706545
MAE: 7.690948135967959
RMSE: 10.811850821069696

 

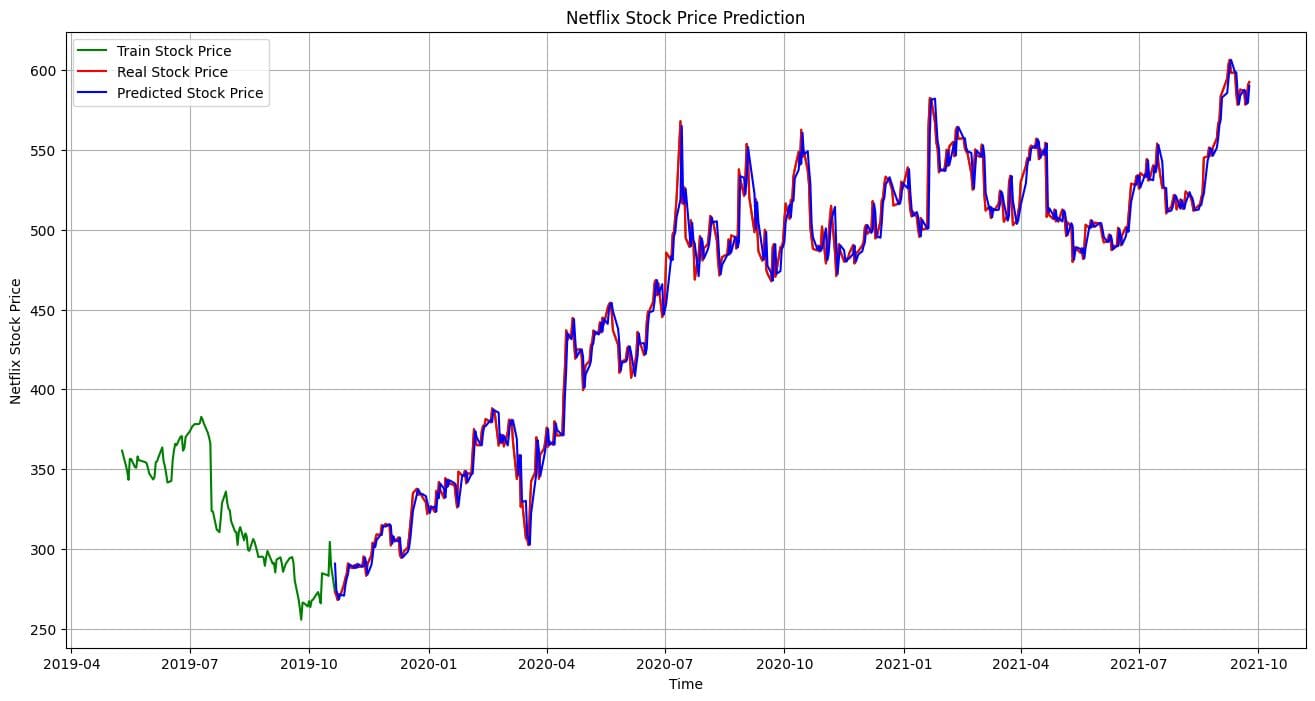
実際の結果と予測結果を視覚化して比較しましょう。明らかに、モデルは非常に正確な予測を行いました。

import matplotlib.pyplot as plt
plt.figure(figsize=(16,8))
plt.plot(net_df.index[-600:], net_df['Open'].tail(600), color='green', label = 'Train Stock Price')
plt.plot(test_data.index, y, color = 'red', label = 'Real Stock Price')
plt.plot(test_data.index, predictions, color = 'blue', label = 'Predicted Stock Price')
plt.title('Netflix Stock Price Prediction')
plt.xlabel('Time')
plt.ylabel('Netflix Stock Price')
plt.legend()
plt.grid(True)
plt.savefig('arima_model.pdf')
plt.show()

 

 

結論

 

この短いチュートリアルでは、ARIMAモデルの概要とPythonでの実装方法について説明しました。ARIMAアプローチは、前の観測値と過去の予測誤差に依存する時間系列データをモデル化する柔軟で構造化された方法を提供します。ARIMAモデルと時系列分析の包括的な分析に興味がある場合は、「Stock Market Forecasting Using Time Series Analysis」を参照することをお勧めします。Abid Ali Awan（@1abidaliawan）は、機械学習モデルの構築が大好きな認定データサイエンティストです。現在、コンテンツ作成と機械学習およびデータサイエンス技術に関する技術ブログの執筆に注力しています。Abidはテクノロジーマネジメントの修士号と通信工学の学士号を保持しています。彼のビジョンは、精神疾患で苦しむ学生向けにグラフニューラルネットワークを使用したAI製品を開発することです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!