「Pymcと統計モデルを記述するための言語の紹介」

Pymc and introduction to statistical modeling language.

前回の記事では、なぜほとんどのベイジアン推論の例がそれが何であるかを誤解しているかについて説明し、ベイジアン統計の初心者の間で共通の誤解を明らかにしました。つまり、ベイジアン統計の分野はベイズの定理の使用によってではなく、不確実性を特徴付けるための確率分布の使用によって定義されるということです。したがって、例えば、既に感染していることを絶対的な確信で知っている場合に、ある医療機器が病気を検出するのに95%の効果があると言われる代わりに、そのデバイスが24%、69%、または91%の効果しかなく、その数値がデバイスからの陽性テスト結果に基づいて感染する確率をどのように変えるかを考慮することができます。モデルでは点推定値（静的なTPRなど）を受け入れず、代わりに確率的なアプローチを選択することで、ベイジアンの確率の視点により忠実になります。

それでは、確率論についてのベイジアンの考え方を獲得するための学習の次のフェーズは、確率的な不確実性の特徴付けにベイジアンの統計モデルを構築することです。これを実現するための最良のツールの1つは、ベイジアン推論と確率的な機械学習モデルの構築に特化して構築されたPyMCのPythonパッケージです。

しかし、ベイジアンモデルの構築を始める前に、このモデルを形成するための言語（つまり、数学的表記法）を実践者に紹介する必要があります。モデルを構築するための言語を理解することは、2つの理由で実用的です：

理由1. 最初の理由は、科学者や研究者などの実践者が適用統計モデル表記法を使用してモデルを形成する方法を学ぶことが、PyMCで実行可能なコードを書く方法と直接関係していることです。モデル表記法を使用することで、統計モデラーは数行の表記でモデルに関する基本的な仮定を伝えることができます。モデルの特性を理解するためにhomoscedasticityのような複雑な単語を覚えることが必要な代わりに、表記法ははるかに簡単なコミュニケーション形式であると主張します。

• 「CHATGPTの内部機能について：AIに関する自分自身の疑問に対するすべての回答」
• 「ケーススタディ：ChatGPT Plusのコードインタプリタを使用してデータと話す」
• 「Pythonによる（バイオ）イメージ解析：Matplotlibを使用して顕微鏡画像を読み込み、ロードする」

理由2. もう1つの理由は、この言語が芸術史から天文学、保全生物学まで、すべての分野に広がっているということです（McElreath、2020）。モデルの記述の言語に慣れることで、科学的コミュニティ間で知識を理解し、伝える範囲を自然に拡大することになります（McElreath、2020）。

適用統計モデル表記法の一般的な紹介として、McElreath教授（2020）は、科学的な議論でモデルを記述し理解するための基礎としていくつかの原則を説明しています：

1. 実践者は、時には観測可能な変数と呼ばれる変数のセットを認識します。これらはデータと呼ばれます。a. 平均値など、データから得られる観測不可能な現象は、パラメータと定義されます。
2. 実践者は、各変数を他の変数に基づいて定義するか、確率分布に基づいて定義します。
3. 変数とその確率分布の組み合わせは、結合生成モデルを定義します。このモデルを使用して仮想的な観測をシミュレートし、実際の観測を分析することができます。

さて、モデル表記の世界の背後にある根拠があるので、おもちゃの例を使ってそれらをどのように使用するかを説明しましょう。あなたは野生でオスのバンクーバーアイランド沿岸オオカミ（Canis lupus crassodon）に出会う確率を量子化することに興味のある保全主義者です。

ちなみに、バンクーバーアイランド沿岸オオカミを例に使用する理由の1つは、最近別の亜種として発見され、分類されたためです。したがって、彼らに関するデータと情報は他のオオカミの亜種と比べて限られており、この亜種の特性に関する推定を行うことは興味深いです。データが限られているだけでなく、私たちの意見では、彼らは他のオオカミの亜種とは異なり、長距離を泳ぐことができ、自然食としてシーフードを取り入れるという非常にクールな動物です（Muñoz‐Fuentes et al.、2009）。より広い観点から見ると、動物の生態学と個体群統計に関する研究は、その動物の保護状況、個体群管理、およびその領域の広範な生態系内での役割の理解に関連する可能性があります。

私たちの例に戻ると、この単純な研究問いに基づいて、バンクーバーアイランド沿岸のオオカミの性比率を数量化する仮定を立て、モデルを構築することができます。まず、この思考実験の結果として起こり得る2つの結果しかないことを前提として、結果の分布が二項分布であると仮定することができます。バンクーバーアイランドを横断する旅の途中で、メスの沿岸オオカミに出会うか、オスに出会うかのいずれかです。実際に、以下のコードを使用して、50%の確率でどちらの二項結果が発生するかをシミュレートすることができます：

# 必要なライブラリのインポートimport arviz as azimport matplotlib.pyplot as pltimport numpy as npimport pandas as pdimport pymc as pmimport scipy.stats as statsaz.style.use("arviz-darkgrid")

x_binom = np.random.binomial(n=10, p=0.5, size=100)sns.histplot(x_binom, kde=True, discrete=True)plt.xlabel(“コインが表に出る回数（N=10）”)plt.ylabel(“サンプルの数”)plt.title('二項分布の可視化')

グラフからわかるように、コインを10回投げた結果に対して正規分布に近い近似値が得られます。x軸はコインが表に出た回数を表し、コードで100回実行した結果に対するy軸はx軸の結果が得られる頻度を示しています。つまり、この実験を100回繰り返すと、およそ30回の実験で10回のうち約5回が表に出る結果が得られます。上記のコードを実行するたびに、グラフの結果はわずかに異なることに注意してください。

また、沿岸オオカミの性比率モデルに別の仮定も取り入れましょう。ここでは、どちらの結果も等しい可能性で発生すると仮定します。二項分布では常にこのようなことが起こるわけではありませんので、デフォルトでこの仮定を行うべきではありません。すべての結果が等しい確率で発生する分布は一様分布と呼ばれます。これは、モデル内の可能な結果について事前の知識がないことを示す方法としてよく使用されます。ただし、十分な練習と経験を積むと、ベイズ派の実践者がモデルを構築する際に現象についてゼロの事前知識を持つことは稀であることがわかります。この分布もグラフで確認したい場合は、次のコードを使用して表示することができます：

x_uni = np.linspace(-.25, 1.25, 100)plt.plot(x_uni, stats.uniform.pdf(x_uni, 0, 1))plt.xlabel("事前確率（性比率）")plt.ylabel("比率の妥当性")plt.title("一様分布の可視化")

沿岸オオカミの性比率モデルの仮定を特定したら、適用統計モデル表記で形式化しましょう：

• M ~ Binomial(N, p): 最初の行は「遭遇するオスの数（M）は、サンプルサイズがNで事前確率がpで二項分布に従って分布する」と解釈することができます。この行は尤度関数を表し、ベイズの定理での証拠の確率P(E | H)、つまり観測された特定の結果の確率を表します。この場合、観測された結果は沿岸オオカミのサンプルデータの結果となります。
• p ~ Uniform(0, 1): 最後に、第2行は「事前確率P(H)は0から1まで一様に分布している」と解釈することができます。

~記号は「～として分布する」という意味で、左側のパラメータがその分布と確率的な関係を持つことを示します。つまり、確率的な関係を表す~記号を見ると、数学的な文の右側の出力が左側の変数（この場合はpまたはM）によって捉えられる分布であることを期待する必要があります。確率的な関係を表現することは、等号=記号を含む数式の出力が分布ではなく単一の数値であることを示す数学的な文とは対照的です。例えば、一般的に線形回帰によく見られるような、y = mx + bという数式の出力は分布ではなく、単一の数値です。

モデルをコードに変換する前に、私たちが必要とする最後のものは、観測のサンプルを生成して、私たちの尤度関数（P(E | H)）を作成することです。再度説明すると、これは与えられた出来事の結果を観測する確率を表しています。例えば、Muñoz-Fuentesと彼女の同僚（2009年）がバンクーバーアイランドの沿岸狼についての研究で取得したサンプルデータを使用すると、28匹のオスが15匹いることが分かります。この場合、私たちの尤度関数は、サンプルデータセットで遭遇した28匹の狼の中から15匹のオスに遭遇する確率として記述することができます。

変数が確立されたので、今度はPyMCを使用して、先ほど形式化したモデル表記を直接コードに組み込むことができます：

# Muñoz-Fuentesら（2009）の研究からサンプルデータセットを読み込む
wolf_samples = "https://raw.githubusercontent.com/vanislekahuna/Statistical-Rethinking-PyMC/main/Data/Vancouver-Island-wolf-samples.csv"
islandwolves_df = pd.read_csv(wolf_samples)
islandwolves_df

# データセット内のオスとメスの比率を決定する
print(f"バンクーバーアイランドの沿岸狼の性別の値の数え上げ：")
print(islandwolves_df["Sexb"].value_counts())

# モデルのサンプル観測を生成する
males = islandwolves_df["Sexb"].value_counts()["M"]
females = islandwolves_df["Sexb"].value_counts()["F"]
total_samples = males + females

### 私たちのPyMCモデル ###
with pm.Model() as wolf_ratio:
  # 事前値の可能な結果の一様分布
  priors = pm.Uniform("uniform_prior", lower=0, upper=1)
  # 一様分布の事前値とサンプルデータ（28匹のうち15匹がオス）から二項分布を生成
  n_males = pm.Binomial("sex_ratio", p=priors, observed=males, n=total_samples)
  # モデルからのサンプルを生成して事後分布を生成
  trace_wolves = pm.sample(1000, tune=1000)
######################

モデルが具現化されたので、もう迷い込んでしまって、最初にモデルを構築した目的を忘れてしまわないようにしましょう。モデルを構築する理由は、確率を定量化することです。分布の可能性においてオスの狼に出くわす確率を、その可能性のランキングに基づいて示すことです。別の言い方をすれば、私たちは、私たちが観測したサンプルデータに基づいて、母集団内のオスとメスの比率を表す事前分布（例：野生の狼のうち1%がオスである、2％、3％、100%まで）において、28匹のうち15匹のオスを観測する確率（尤度関数）に興味があります。ここでの最終結果は、私たちが観測したサンプルデータに基づいて最もあり得るオスとメスの比率を示す事後確率分布です。上記のコードでは、事後分布は`trace_wolves`オブジェクトにキャプチャされており、私たちが構築したモデルをサンプリングすることで結果の事後確率を生成します。気になるかもしれませんが、事後分布を生成するために使用されるサンプリング手法については、後の記事でカバーすることができます。PyMCはいくつかの選択肢を提供しており、それぞれが独自の深い穴になっています。

以下の左側のグラフは、事後分布の結果を可視化したもので、x軸は性別比率の事前確率分布を、y軸はその比率の妥当性を表しています：

az.plot_trace(trace_wolves)

そして、Bayesの定理の変数として構築した`wolf_ratio`モデルを構造化するのが役立つ場合は、次のようにすることができます：

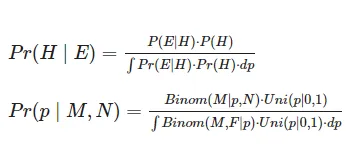
再度強調すると、ここでの目標は、分布内の各事前値に対するあり得る事後確率の分布を生成することです。最も確率の高い性別比率を見つけることを目指しているわけではありません。ただし、もし興味があるのであれば、PyMCの`find_map`関数を使用して、事後分布内で最も確率の高い事前値（つまり、最もあり得るオスとメスの比率）を求めることができます。

pm.find_MAP(model=wolf_ratio)

または、Arvizの `summary` 関数も使えます。これは、事後分布の最大事前確率（MAP）に加えて、分布の89%を含む最高密度区間（時には互換性区間とも呼ばれる）も表示します。

az.summary(trace_wolves, round_to=2, kind="stats", hdi_prob=0.89)

以上です。これで、ほとんどの学術研究で使用される統計モデル表記の基本的な紹介を終えました。そして、モデル表記を最初のPyMCモデルに統合しました。このモデルでは、バンクーバーアイランドの沿岸オオカミの雄の性比率について何も知らない場合の野生での遭遇の可能性をシミュレーションしました。モデル表記に慣れることは、PyMCを使用してより複雑なベイジアンモデルを構築するための堅固な基盤となります。このトピックに関するさらなるブログ記事を近い将来に公開する予定ですので、お楽しみに！

参考文献:

McElreath, R. (2020). Statistical Rethinking: A Bayesian Course with examples in R and Stan. Routledge.

Muñoz‐Fuentes, V., Darimont, C. T., Wayne, R. K., Paquet, P. C., & Leonard, J. A. (2009). Ecological factors drive differentiation in wolves from British Columbia. Journal of Biogeography, 36(8), 1516–1531. https://www.raincoast.org/files/publications/papers/Munoz_et_al_2009_JBiogeog.pdf

Muñoz-Fuentes, V., Darimont, C.T., Paquet, P.C., & Leonard, J.A. (2010). The genetic legacy of extirpation and re-colonization in Vancouver Island wolves. Conservation Genetics, 11, 547–556. https://digital.csic.es/bitstream/10261/58619/1/evol.pdf

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!