近接度とコミュニティ:PythonとNetworkXによるソーシャルネットワークの分析—Part 3
Proximity and Community Social Network Analysis with Python and NetworkX - Part 3
PythonとNetworkXを使って、社会ネットワーク分析におけるコミュニティと近接中心性について学ぼう
第2部では、Smashing PumpkinsとZwanのバンドメンバーの関係をグラフ化し、次数中心性や媒介中心性などのメトリックを用いて、異なるバンドのメンバー間の関係を調べました。同時に、ドメイン知識が結果の理解にどのように役立つかについても議論しました。
第3部では、近接中心性の基本的な概念とその計算方法について説明し、Billy Corganのネットワークを例にして、NetworkXを使用して近接中心性を計算する方法を実演します。
始める前に…
- Pythonの基本的な知識を持っていますか?持っていない場合は、こちらから始めてください。
- ノードやエッジなど、社会ネットワーク分析の基本的な概念について理解していますか?それでない場合は、こちらから始めてください。
- 次数中心性や媒介中心性に慣れていますか?そうでない場合は、こちらから始めてください。
近接中心性とコミュニティ
近接中心性
近接中心性は、社会ネットワーク分析における指標の1つで、ネットワーク内のすべてのノードとの最短経路距離を考慮して、ノードがどの程度近くにあるかを定量化するものです。
近接中心性は、ネットワーク内での情報やリソースの流れの効率性に焦点を当てています。つまり、近接中心性が高いノードは、ネットワーク内の他のノードにより早くかつ効率的に到達できるため、ネットワーク内の他のノードとの平均距離が短くなります。
ノードの近接中心性は、そのノードからネットワーク内のすべての他のノードまでの最短経路距離(SPD)の逆数として計算されます。
近接中心性 = 1 / (ノードからすべての他のノードへのSPDの合計)
値が高いほど、ネットワーク内での情報の流れの中心的で効率的な役割を果たしています。
近接中心性の計算方法
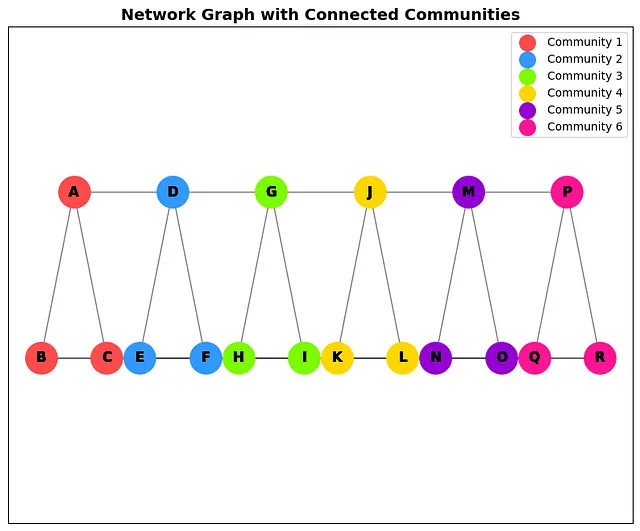
ここでは、8つのノードからなる単純なネットワークを使用して説明します。
- ノードAからすべての他のノードまでの最短経路距離(SPD)を計算します。例として、簡単な距離を使用します。実際には、幅優先探索やダイクストラのアルゴリズムなどの最短経路アルゴリズムを使用して計算されます。
2. ノードAからすべての他のノードまでの最短経路距離の合計を計算します。
3. 近接中心性の式を適用します。
近接中心性とコミュニティ
コミュニティは、グループ内のノードが、グループ外のノードと比較してより密に接続されているようなノードのグループとして考えることができます。コミュニティは、ネットワーク内の密集したサブグループやモジュールのアイデアを捉え、同じコミュニティ内のノードが互いに強いつながりを持っていることを特徴としています。コミュニティは、密な内部コネクションと比較的疎な外部コネクションの存在によって特徴づけられます。
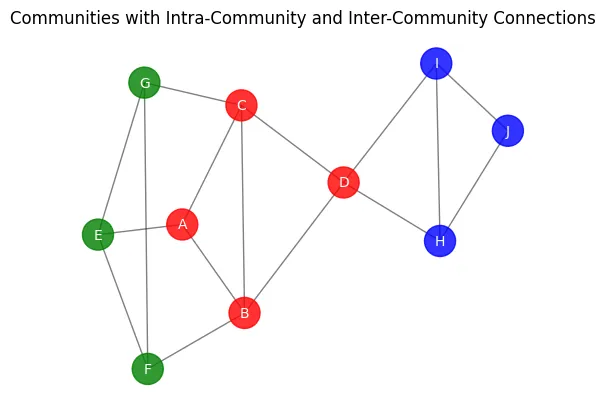
Smashing PumpkinsとZwanのメンバーを考えると、両バンドのメンバーが共有することで互いに繋がっていることが想像できます。これは、それぞれのバンド内のメンバー間の内部グループの連結性と、両バンド間の外部グループの連結性を示しています。
近接中心性は個々のノードの重要性と情報フローの効率性を測定する一方、コミュニティは密接な接続を持つ凝集サブグループを捕捉します。これらの両方が合わさって、情報フローのダイナミクスとネットワークの構成を理解するために貢献します。
近接中心性とコミュニティを使ってネットワークダイナミクスを解釈するためのいくつかの方法について議論しましょう。
- コミュニティ内の近接中心性
同じコミュニティに属するノードはしばしばコミュニティ内でより高い近接中心性値を持ちます。これは、コミュニティ内のノードが密接に接続されており、最短経路距離において迅速に到達できることを示しています。コミュニティ内でのより高い近接中心性は、サブグループ内の効率的な情報フローとコミュニケーションを反映しています。

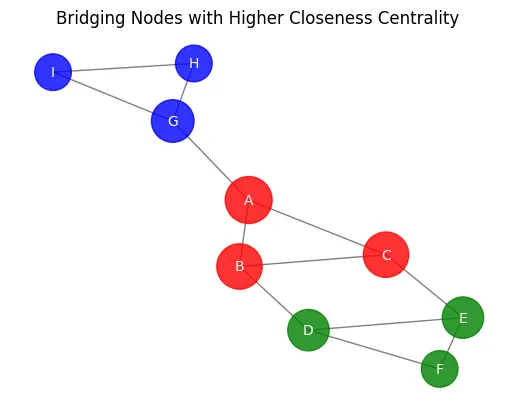
2. 近接中心性によるコミュニティの橋渡し
異なるコミュニティを接続するノード、またはコミュニティ間を橋渡しする役割を果たすノードは、個別のコミュニティ内のノードに比べてより高い近接中心性を持つ場合があります。これらのノードは、別々のコミュニティを接続し、それらの間のコミュニケーションと情報フローを促進する重要な役割を果たします。
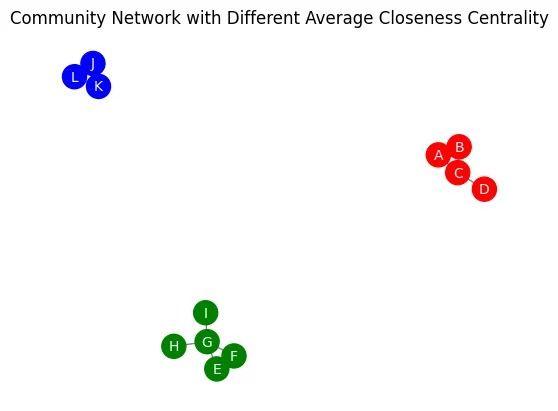
3. 近接中心性を用いたコミュニティレベルの分析
近接中心性は、ネットワーク内のコミュニティの重要性を分析するためにも使用できます。コミュニティ内のノードの近接中心性値を集計することで、コミュニティ内の情報フローの全体的な効率性を評価できます。平均近接中心性が高いコミュニティは、ネットワーク内で情報にアクセスし、それを発信する能力においてより中心的かつ影響力があると考えられます。
近接中心性は個々のノードの重要性と情報フローの効率性を測定する一方、コミュニティは密接な接続を持つ凝集サブグループを捕捉します。これらの両方が合わさって、情報フローのダイナミクスとネットワークの構成を理解するために貢献します。
Billy Corganの影響範囲を考慮する場合、近接中心性はSmashing PumpkinsやZwanのメンバーがBilly Corganのネットワーク内の他のミュージシャンに直接的にも間接的にもどのように影響を与えるかを示す洞察を提供することができます。私たちは、それぞれのバンドを説明するためにコミュニティの概念を使用できますが、両方のバンドの集約を説明するためにも使用できます。現実には、1990年代のオルタナティブロックミュージシャンのコミュニティは広大であり、ネットワークにさらにバンドを追加すると、より多くのコミュニティが現れます。

PythonでのNetworkXにおける近接中心性
- Part 2 で行ったように、各バンドのバンドメンバーのすべての組み合わせを生成する関数を作成します。
2. 次に、各バンドを定義し、関数を適用してタプルのリストを生成します。そして、リストを結合して、重複を除くためにリスト内包表記を使用します。
3. これでグラフを描画することができます。
次のようになるはずです:
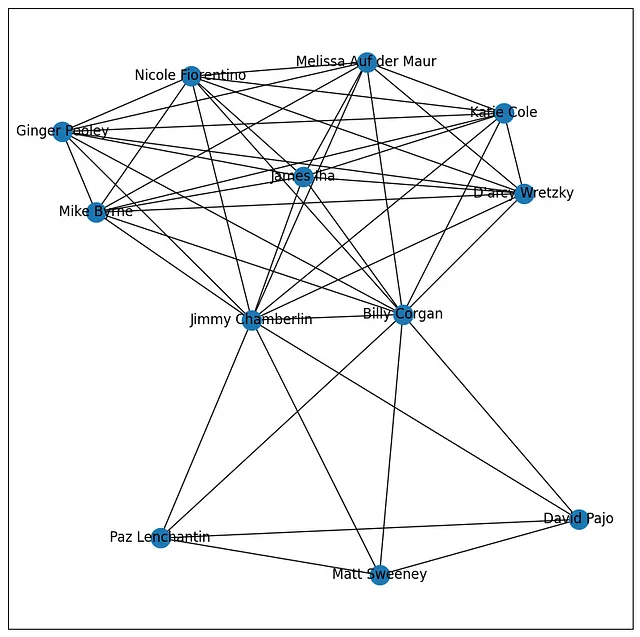
4. 最後に、中心性の近さを計算して値を分析しましょう。
出力は以下のようになります:
これらの値について何が言えるでしょうか?
- Billy CorganとJimmy Chamberlinは、最も中心的なメンバーであり、他のメンバーに迅速に到達するために最も適した中心性の近さ1.00を持っています。
- James Iha、Katie Cole、D’arcy Wretzky、Melissa Auf der Maur、Ginger Pooley、Mike Byrne、およびNicole Fiorentinoは、0.785714という同じ中心性の近さの値を持っています。これは、これらのメンバーが密接に関連しており、互いに迅速に到達できることを示しています。
- Paz Lenchantin、David Pajo、およびMatt Sweeneyは、0.611111というわずかに低い中心性の近さの値を持っています。これは、前のグループと比較して他のメンバーに到達するための中心的な存在ではない可能性があることを示していますが、ネットワーク内で比較的よく接続されていることを示しています。
まだ比較的単純なネットワークを扱っているため、これらの結果はBilly Corganのネットワークの次数中心性と媒介中心性を計算したときに学んだことを超えるものは示しません。第4部では、より多くのバンドやミュージシャンをネットワークに加えることで複雑さを増し、さらに魅力的なNetworkXグラフを作成するための高度なMatplotlibのテクニックを紹介します!
完全に注釈付きのPythonチュートリアルをご希望の場合は、私のGitHubをご覧ください!
👩🏻💻 Christine Egan | VoAGI | github | linkedin
VoAGIに私の紹介リンクで参加してください – Christine Egan
VoAGIのメンバーとして、お読みいただいた作家に対してメンバーシップ料金の一部が支払われ、すべてのストーリーに完全にアクセスできます…
VoAGI.com
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
