PIDコントローラの最適化：勾配降下法のアプローチ

PIDコントローラの最適化：勾配降下法

機械学習を用いてエンジニアリング最適化問題を解決する

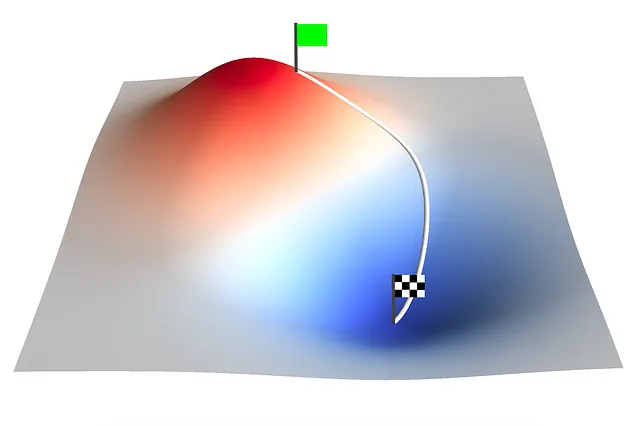
機械学習。ディープラーニング。AI。これらの技術を使う人々がますます増えています。これは、ChatGPT、Bardなどによって展開された大規模言語モデルの台頭によるものです。しかし、これらの技術の根本にある手法に詳しい人は比較的少ないです。

この記事では、機械学習で展開される基本的な手法の1つである勾配降下法アルゴリズムについて詳しく説明します。

勾配降下法をニューラルネットワークの観点から見るのではなく、クラシックなエンジニアリング最適化問題を解決するためのツールとしてアルゴリズムを調査します。

具体的には、勾配降下法を使用して、自動車のクルーズコントロールシステムのPID（比例積分微分）コントローラのゲインを調整します。

• あなたの製品の開発者学習のためのLLM（大規模言語モデル）
• 「WebAgentに会いましょう：DeepMindの新しいLLM、ウェブサイト上での指示に従ってタスクを完了する」
• 「2023年に知っておくべきすべての大規模言語モデル（LLM）」

このアプローチを取る動機は2つあります：

まず、ニューラルネットワークの重みとバイアスを最適化することは高次元の問題です。多くの要素があり、これらは勾配降下法による最適化問題の本質から注意を逸らすと思います。

さらに、後で見るように、勾配降下法はPIDコントローラのチューニング、ロボット工学の逆運動学、トポロジー最適化などのクラシックなエンジニアリング問題に適用すると強力なツールになります。私の意見では、勾配降下法は、より多くのエンジニアが理解し、利用できるべきツールです。

この記事を読むことで、PIDコントローラとは何か、勾配降下法アルゴリズムの動作原理、そしてクラシックなエンジニアリング最適化問題を解決するためにそれがどのように適用されるかを理解することができます。あなた自身の最適化の課題に勾配降下法を利用する意欲が湧くかもしれません。

この記事で使用されるすべてのコードは、こちらのGitHubで入手できます。

PIDコントローラとは何ですか？

PIDコントローラは、エンジニアリングや自動化システムで広く使用されるフィードバック制御機構です。目標設定値を維持するために、制御信号を連続的に調整し、目標設定値とシステムの測定出力（プロセス変数）との誤差に基づいています。

PIDコントローラは、製造業における温度制御、化学プラントにおける流量制御、HVACシステムにおける圧力制御など、さまざまな産業やドメインで幅広く使用されています。PIDコントローラは、ロボット工学において精密な位置決めやモーション制御、自動車システムにおけるスロットル制御、エンジン回転数制御、ABS（アンチロックブレーキシステム）にも使用されています。また、航空宇宙および航空の応用においても、航空機の自動操縦装置や姿勢制御システムなどに重要な役割を果たしています。

PIDコントローラは、比例項、積分項、微分項の3つの要素で構成されています。比例項は現在の誤差に対して直ちに応答し、積分項は過去の誤差を蓄積して修正し、微分項は将来の誤差の傾向を予測し対策を講じます。

PIDコントローラの制御ループは、上記のブロックダイアグラムに示されています。r(t)は目標設定値であり、y(t)はプロセス変数です。プロセス変数から目標設定値を引いて、誤差信号e(t)を得ます。

制御信号u(t)は比例項、積分項、微分項の合計です。制御信号はプロセスに入力され、これによってプロセス変数が更新されます。

PIDコントローラの制御信号u(t)

勾配降下法アルゴリズム

勾配降下法は、機械学習や数理最適化で一般的に使用される最適化アルゴリズムです。これは、与えられたコスト関数の最小値を見つけるために、パラメータをコスト関数の勾配に基づいて反復的に調整します。勾配は最も急な上昇方向を指し示すため、逆方向にステップを取ることで、アルゴリズムは徐々に最適解に収束していきます。

単一の勾配降下更新ステップは次のように定義されます：

勾配降下更新ステップ

ここで、aₙは入力パラメータのベクトルです。添字nはイテレーションを示します。f(aₙ)は多変数のコスト関数であり、∇f(a)はそのコスト関数の勾配です。∇f(aₙ)は最も急な上昇方向を表しているため、次のイテレーションでコスト関数を減らすためにaₙから引かれます。𝛾は学習率であり、各イテレーションでのステップサイズを決定します。

適切な𝛾の値を選択する必要があります。大きすぎると、各イテレーションでのステップが大きすぎて勾配降下アルゴリズムが収束しなくなります。小さすぎると、勾配降下アルゴリズムは計算コストが高く、収束するまでに長い時間がかかります。

勾配降下は、様々な分野や学問で応用されています。機械学習やディープラーニングでは、ニューラルネットワークのトレーニングやパラメータの最適化に使用される基本的な最適化アルゴリズムです。コスト関数の勾配に基づいてネットワークの重みとバイアスを反復的に更新することで、勾配降下はネットワークが学習し、性能を向上させることができます。

機械学習を超えて、勾配降下はエンジニアリング、物理学、経済学、およびその他の領域でさまざまな最適化問題に利用されています。パラメータ推定、システム同定、信号処理、画像再構成など、関数の最小値または最大値を見つける必要があるタスクにおいて、勾配降下は最適化問題の解決やモデルやシステムの改善に不可欠なツールです。勾配降下の汎用性と効果性により、さまざまな分野で最適化問題の解決やモデルやシステムの改善が可能となっています。

勾配降下を使用したPIDコントローラのゲインの最適化

PIDコントローラのチューニングにはいくつかの方法があります。これには手動チューニング法やZiegler-Nichols法などのヒューリスティックな方法があります。手動チューニング法は時間がかかる場合があり、最適な値を見つけるために複数の反復が必要になる場合があります。一方、Ziegler-Nichols法はしばしば攻撃的なゲインと大きなオーバーシュートをもたらすため、特定のアプリケーションには適していません。

ここでは、PIDコントローラの最適化に勾配降下法を適用します。ステップセットポイントに対して車のクルーズコントロールシステムの制御システムを最適化します。

コントローラの目的は、ペダル位置を制御して、最小のオーバーシュート、定常時間、および定常状態の誤差で車を設定速度まで加速することです。

車はペダル位置に比例した駆動力にさらされます。転がり抵抗と空気抵抗力は、駆動力とは逆方向に働きます。ペダル位置はPIDコントローラによって制御され、-50％から100％の範囲内に制限されます。ペダル位置が負の場合、車はブレーキをかけています。

PIDコントローラゲインのチューニング時にシステムのモデルを持つことは役立ちます。これにより、システムの応答をシミュレートすることができます。PythonでCarクラスを実装しました：

import numpy as npclass Car:    def __init__(self, mass, Crr, Cd, A, Fp):        self.mass = mass # [kg]        self.Crr = Crr # [-]        self.Cd = Cd # [-]        self.A = A # [m^2]        self.Fp = Fp # [N/%]        def get_acceleration(self, pedal, velocity):        # Constants        rho = 1.225 # [kg/m^3]        g = 9.81 # [m/s^2]        # Driving force        driving_force = self.Fp * pedal        # Rolling resistance force        rolling_resistance_force = self.Crr * (self.mass * g)        # Drag force        drag_force = 0.5 * rho * (velocity ** 2) * self.Cd * self.A        acceleration = (driving_force - rolling_resistance_force - drag_force) / self.mass        return acceleration        def simulate(self, nsteps, dt, velocity, setpoint, pid_controller):        pedal_s = np.zeros(nsteps)        velocity_s = np.zeros(nsteps)        time = np.zeros(nsteps)        velocity_s[0] = velocity        for i in range(nsteps - 1):            # Get pedal position [%]            pedal = pid_controller.compute(setpoint, velocity, dt)            pedal = np.clip(pedal, -50, 100)            pedal_s[i] = pedal            # Get acceleration            acceleration = self.get_acceleration(pedal, velocity)                        # Get velocity            velocity = velocity_s[i] + acceleration * dt            velocity_s[i+1] = velocity            time[i+1] = time[i] + dt                return pedal_s, velocity_s, time

クラスPIDControllerは以下のように実装されています：

class PIDController:    def __init__(self, Kp, Ki, Kd):        self.Kp = Kp        self.Ki = Ki        self.Kd = Kd        self.error_sum = 0        self.last_error = 0        def compute(self, setpoint, process_variable, dt):        error = setpoint - process_variable                # 比例項        P = self.Kp * error                # 積分項        self.error_sum += error * dt        I = self.Ki * self.error_sum                # 微分項        D = self.Kd * (error - self.last_error)        self.last_error = error                # PID 出力        output = P + I + D                return output

このオブジェクト指向のプログラミングアプローチを取ることで、勾配降下法を実行する際に異なる PID コントローラのゲインで複数のシミュレーションを設定して実行することが容易になります。

クラスGradientDescentは以下のように実装されています：

class GradientDescent:    def __init__(self, a, learning_rate, cost_function, a_min=None, a_max=None):        self.a = a        self.learning_rate = learning_rate        self.cost_function = cost_function        self.a_min = a_min        self.a_max = a_max        self.G = np.zeros([len(a), len(a)])        self.points = []        self.result = []        def grad(self, a):        h = 0.0000001        a_h = a + (np.eye(len(a)) * h)        cost_function_at_a = self.cost_function(a)        grad = []        for i in range(0, len(a)):            grad.append((self.cost_function(a_h[i]) - cost_function_at_a) / h)        grad = np.array(grad)        return grad        def update_a(self, learning_rate, grad):        if len(grad) == 1:            grad = grad[0]        self.a -= (learning_rate * grad)        if (self.a_min is not None) or (self.a_min is not None):            self.a = np.clip(self.a, self.a_min, self.a_max)        def update_G(self, grad):        self.G += np.outer(grad,grad.T)        def execute(self, iterations):        for i in range(0, iterations):            self.points.append(list(self.a))            self.result.append(self.cost_function(self.a))            grad = self.grad(self.a)            self.update_a(self.learning_rate, grad)        def execute_adagrad(self, iterations):        for i in range(0, iterations):            self.points.append(list(self.a))            self.result.append(self.cost_function(self.a))            grad = self.grad(self.a)            self.update_G(grad)            learning_rate = self.learning_rate * np.diag(self.G)**(-0.5)            self.update_a(learning_rate, grad)

アルゴリズムは、executeまたはexecute_adagradを呼び出すことで指定された回数のイテレーションで実行されます。 execute_adagradメソッドは、アダプティブ勾配降下法と呼ばれる勾配降下法の変形形式を実行します。

AdaGradは、疎なパラメータに対して学習率が増加し、より疎でないパラメータに対して学習率が減少するパラメータごとの学習率を持っています。学習率は、勾配の二乗の過去の合計に基づいて各イテレーションの後に更新されます。

AdaGradを使用して、車のクルーズコントロールシステムの PID コントローラのゲインを最適化します。アダグラッドを使用することで、勾配降下の更新方程式は次のようになります：

アダグラッド勾配降下の更新ステップ

次に、コスト関数を定義する必要があります。コスト関数は、入力パラメータのベクトルを入力とし、単一の数値であるコストを返す必要があります。車のクルーズコントロールの目的は、最小のオーバーシュート、収束時間、定常状態誤差で目標速度まで車を加速することです。この目的に基づいて、多くの方法でコスト関数を定義することができます。ここでは、時間にわたる誤差の絶対値の積分として定義します：

車のクルーズコントロールのコスト関数

コスト関数は積分であるため、誤差の絶対値曲線の下の面積として視覚化できます。グローバルな最小値に近づくにつれて、曲線の下の面積が減少することを期待しています。プログラム的には、コスト関数は次のように定義されます：

def car_cost_function(a):    # 車のパラメータ    mass = 1000.0  # 車の質量 [kg]    Cd = 0.2  # 空気抵抗係数 []    Crr = 0.02 # 転がり抵抗係数 []    A = 2.5 # 車の正面面積 [m^2]    Fp = 30 # % ペダル位置あたりの駆動力 [N/%]    # PIDコントローラのパラメータ    Kp = a[0]    Ki = a[1]    Kd = a[2]    # シミュレーションのパラメータ    dt = 0.1  # タイムステップ    total_time = 60.0  # 総シミュレーション時間    nsteps = int(total_time / dt)    initial_velocity = 0.0  # 車の初期速度 [m/s]    target_velocity = 20.0 # 車の目標速度 [m/s]    # CarとPIDControllerオブジェクトを定義    car = Car(mass, Crr, Cd, A, Fp)    pid_controller = PIDController(Kp, Ki, Kd)    # シミュレーションを実行    pedal_s, velocity_s, time = car.simulate(nsteps, dt, initial_velocity, target_velocity, pid_controller)    # コストを計算    cost = np.trapz(np.absolute(target_velocity - velocity_s), time)    return cost

コスト関数にはシミュレーションパラメータが含まれています。シミュレーションは60秒間実行されます。この時間内に、セットポイントを0 m/sから20 m/sにステップ変更した際のシステムの応答を観察します。時間の経過とともに誤差の大きさを積分し、各イテレーションでコストを計算します。

さて、残りのことは最適化を実行するだけです。初期値としてKp = 5.0、Ki = 1.0、Kd = 0.0を使用します。これらの値は、セットポイントに収束する過渡応答を持ち、オーバーシュートが発生します。この開始点から、学習率𝛾=0.1を使用して500回のイテレーションで勾配降下法アルゴリズムを実行します：

a = np.array([5.0, 1.0, 0.0])gradient_descent = GradientDescent(a, 0.1, car_cost_function, a_min=[0,0,0])gradient_descent.execute_adagrad(500)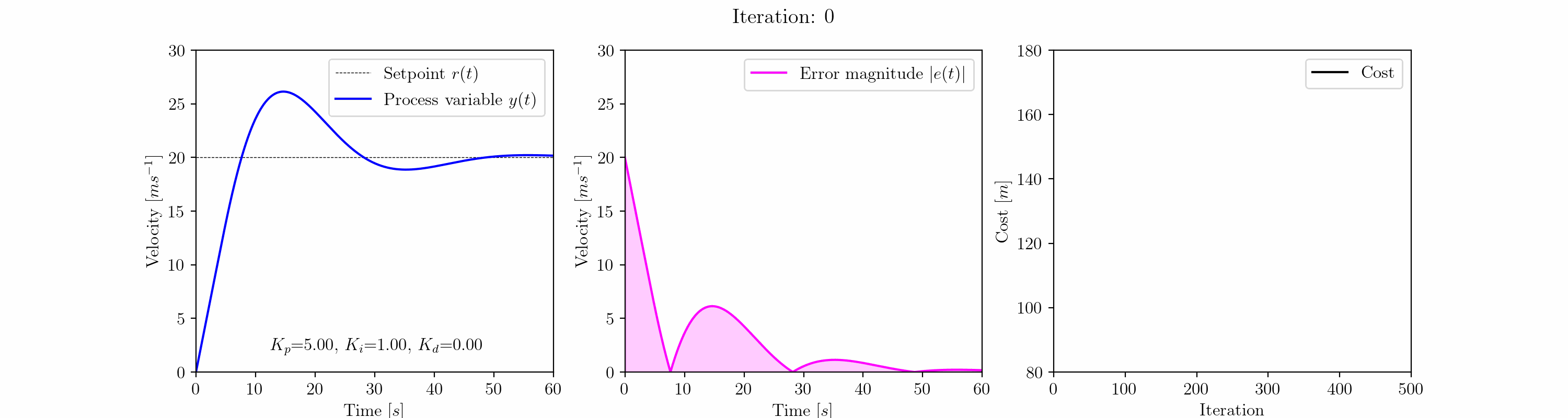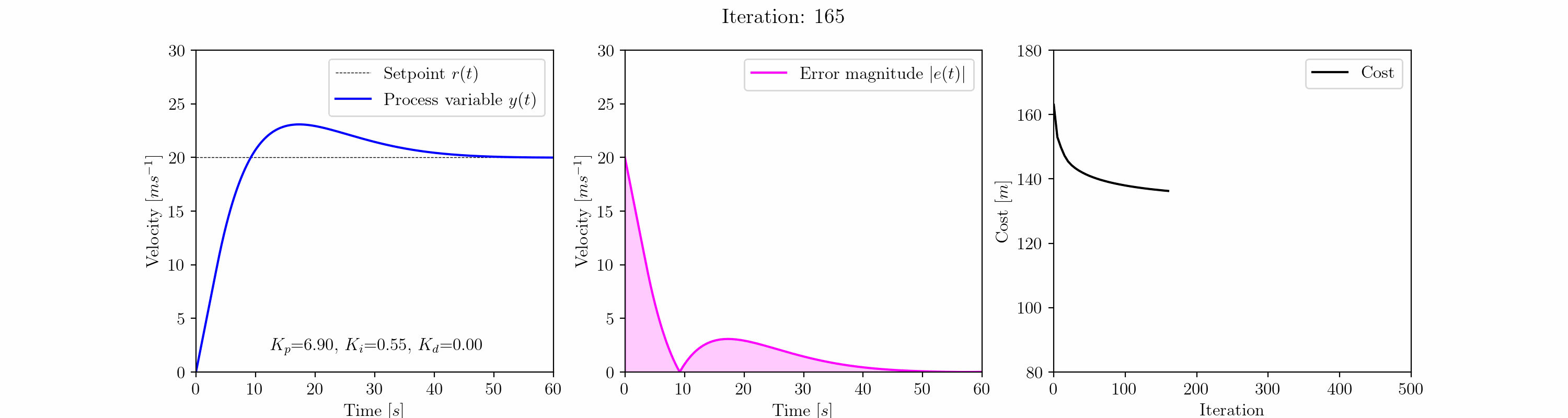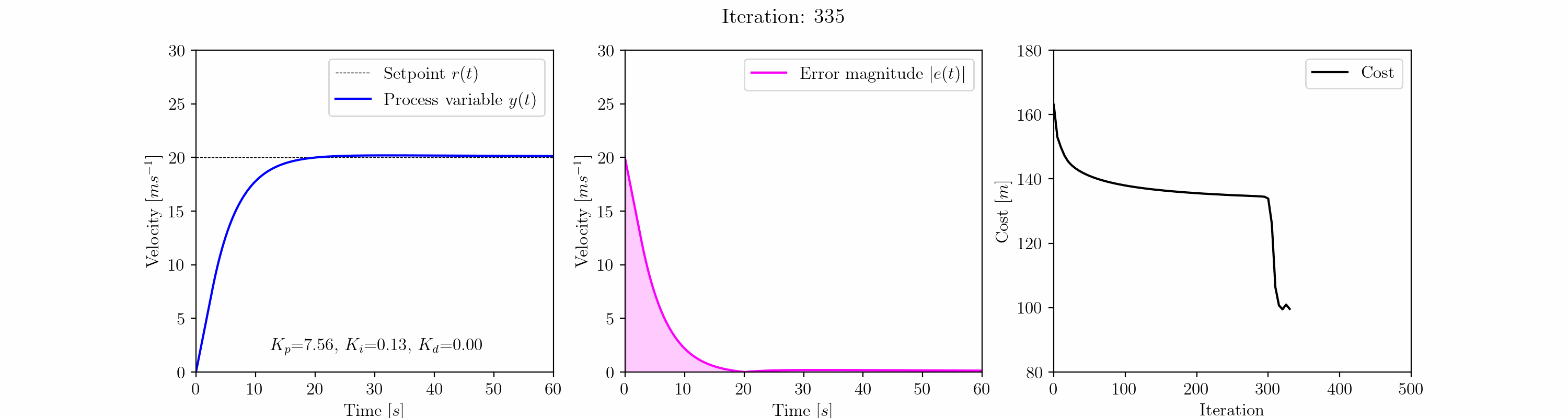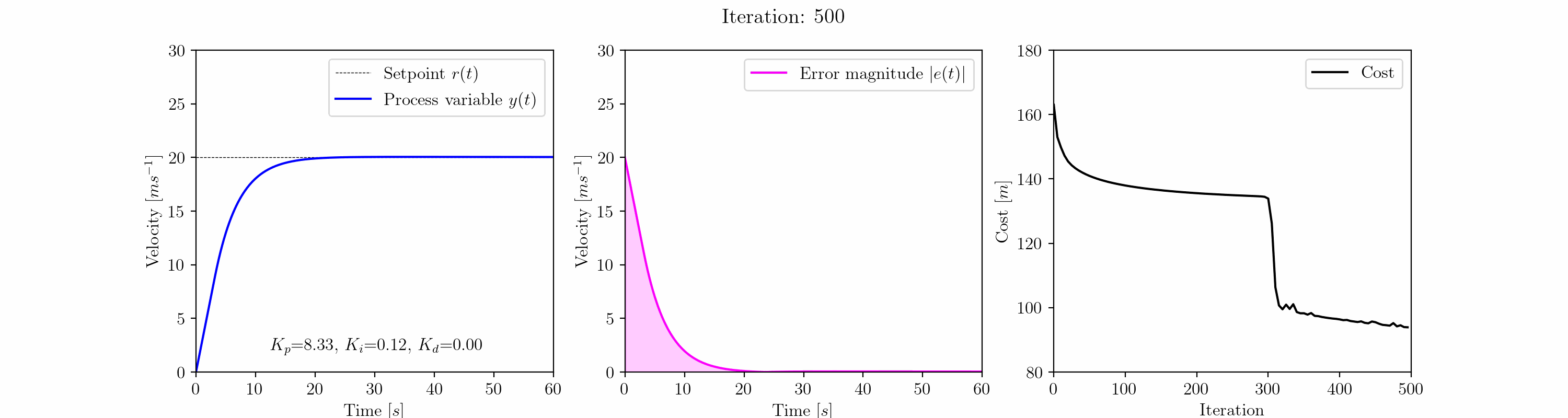

上記のアニメーションプロットは、勾配降下法アルゴリズムがPIDコントローラのKp、Ki、Kdゲインを調整する過程での車のクルーズコントロールのステップ応答の進化を示しています。

イテレーション25までに、勾配降下法アルゴリズムは振動応答を除去しています。このポイント以降、興味深いことが起こります。アルゴリズムは、Kpが6.0＜Kp＜7.5、Ki≈0.5、Kd=0.0の範囲で特徴付けられるオーバーシュート（約3 m/s）の局所最小値に入ります。この局所最小値はイテレーション300まで続きます。

イテレーション300以降、アルゴリズムは局所最小値から抜け出し、より満足のいく応答を得るためにグローバル最小値に近い応答を見つけます。この応答はオーバーシュートがゼロで、高速な収束時間を持ち、ほぼゼロの定常誤差で特徴付けられます。

500回のイテレーションで勾配降下法アルゴリズムを実行することで、最適化されたPIDコントローラのゲインであるKp = 8.33、Ki = 0.12、Kd = 0.00に到達します。

比例ゲインはまだ着実に上昇しています。さらに多くのイテレーションを実行することで（ここでは示されていません）、Kpが徐々に増加するにつれて、コスト関数のさらなる削減が可能であることがわかりますが、この効果はますます限定的になります。

まとめ

機械学習やディープラーニングの問題を解決するために広く使用されている手法を採用し、車のクルーズコントロールシステムのPIDコントローラのゲインを最適化しました。

Kp = 5.0、Ki = 1.0、Kd = 0.0という初期値を使用し、勾配降下法アルゴリズムのAdaGrad形式を適用することで、この低次元のシステムが最初に局所最小値に入り、最終的にはオーバーシュートがゼロで、高速な収束時間を持ち、ほぼゼロの定常誤差でより満足のいく応答を見つける様子を観察しました。

この記事では、勾配降下法が古典的なエンジニアリングの最適化問題に適用される際の強力なツールであることを見てきました。ここで示された例以外にも、勾配降下法はロボット工学の逆運動学、トポロジーオプティマイゼーションなど、他のエンジニアリングの問題の解決に利用することができます。

勾配降下法が適用できる最適化問題はありますか？コメントで教えてください。

この記事をお楽しみいただけましたか？

フォローして購読し、ネットワークで共有して、自分自身の最適化問題に勾配降下法を適用してみてください。

すべての画像は、特に記載がない限り、著者によるものです。

参考文献

Web

[1] GitHub（2023年）、pid_controller_gradient_descent

[2] Wikipedia（2023年）、Ziegler–Nichols method（2023年7月10日アクセス）

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!