ローゼンブラットのパーセプトロンによる分類

Perceptron classification by Rosenblatt

機械学習の「Hello World」

最近、私は機械学習の最も基本的な導入とは何かを考えていました。私は単純なタスク、例えば2値分類と、短い記事で説明できるほど十分に単純なアルゴリズムを求めていました。アルゴリズムにはある程度の歴史がある方が良いです。候補を見つけるのにあまり時間はかかりませんでした：パーセプトロンです。パーセプトロンは機械学習の始まりに連れて行ってくれます。それは60年以上前にFrank Rosenblattによって導入されました。パーセプトロンルールはニューロンのように、複数の入力特徴を取り、入力特徴ベクトルと乗算される重みをフィットさせることで、ニューロンが信号を出力するかどうか、または機械学習の分類コンテキストでは出力が0または1であるかどうかの決定を行います。パーセプトロンはおそらく最も単純な2値分類器であり、現在でも実際に使用される機械学習のユースケースは知られていません。しかし、ニューラルネットワークの道を開いた教育的および歴史的な価値があります。

この記事の目的はパーセプトロンを紹介し、単純な2値分類タスクで使用することです。パーセプトロンはscikit-learnで実装されていますが、それに頼らずにゼロから構築します。また、アルゴリズムがどのように決定境界を設定し、収束を覗くための可視化も作成します。パーセプトロンは、フィッティングプロセス中に同時に反復的に調整される重みとバイアス項からなる線形モデルです。ただし、連続的な損失関数は持っておらず、おそらく機械学習の歴史の中で直接の後継者であるアダプティブリニアニューロン（Adaline）アルゴリズムと同様に、シングルレイヤーニューラルネットワークです。パーセプトロンのフィッティングは単に誤分類サンプルの検出に依存し、誤分類サンプルが発生すると重みとバイアスが直ちに更新されます。エポックごとではなく、エポックごとに一度の更新（エポックはトレーニングセットを完全に通過すること）は必要ありません。したがって、アルゴリズムには最適化器さえ必要ありません。それはとてもシンプルでエレガントで美しいと言えるでしょう。それがどのように動作するか気になる方はお楽しみに！

パーセプトロンの理論

パーセプトロンは、他の線形モデルと同様に、各特徴量に対して重みのセットを使用し、予測を生成するために重みと特徴値の内積を計算し、バイアスを加えます。

• OpenAIとLangChainによるMLエンジニアリングとLLMOpsへの導入
• 「機械学習を利用した資産の健全性とグリッドの耐久性の向上」
• 「Amazon Rekognition、Amazon SageMaker基盤モデル、およびAmazon OpenSearch Serviceを使用した記事のための意味論的画像検索」

この線形関数の結果、またネット入力とも呼ばれるものは、パーセプトロンの場合は単純なステップ関数である活性化関数f(z)に供給されます。つまり、f(z)はz≥0の場合に1の値を取り、それ以外の場合は0を取ります。活性化関数の役割は、ネット入力を0と1の2つの値にマッピングすることです。基本的には、私たちが行ったことは、超平面を定義することです。超平面の同じ側にあるポイントは同じクラスに属します。重みは超平面に垂直なベクトルを定義し、つまり超平面の方向を定義し、バイアスは原点からの超平面の距離を定義します。フィッティングプロセスが開始されると、ランダムに方向が設定された超平面がランダムな距離で存在します。誤分類サンプルに出くわすたびに、超平面を少し押し動かし、その方向と位置を変えて、次のエポックでサンプルが超平面の右側にあるようにします。超平面をどれだけ押し動かすか、つまり学習率をどうするかは私たちが決めることができます。

通常、全てのサンプルをいくつかのエポック（回）にわたって通過する必要があります。全てのポイントが誤分類されていない、またはより正確に言えば進歩がなくなるまでです。各エポックでは、トレーニングセットのすべてのサンプルi = 1,.., nₛₐₘₚₗₑₛをループし、現在の重みとバイアスを使用してモデルが誤分類されているかどうかを調べ、誤分類されている場合は学習率ηを使用してすべての重みj=1,.., nfₑₐₜᵤᵣₑₛを更新します：

where

予測結果を示すハットを使用して更新します。

バイアスも次のように更新されます。

これらの操作を行う理由は概念的には簡単です。モデルがクラス0を予測した場合、正しいクラスが1であるとします。xⱼが正の場合、重みは増加し、ネット入力が増加します。xⱼが負の場合、重みは減少し、ネット入力が再び増加します（重みの符号に関係なく）。同様に、バイアスも増加し、ネット入力がさらに増加します。これらの変更により、次のエポックで誤分類されたサンプルの正しいクラスを予測する可能性が高くなります。モデルがクラス1を予測した場合、正しいクラスが0であるという論理も同様であり、唯一の違いはすべての符号が反転することです。

注意してみると、同じエポック内で重みとバイアスが複数回更新されることに気づくでしょう。誤分類されたサンプルごとに一度ずつ更新されます。各誤分類は、決定境界ハイパープレーンを再配置し、再方向付けして、次のエポックでサンプルが正しく予測されるようにします。

データの準備

2つのガウス分布からなる合成データセットを使用します。パーセプトロンは任意の次元の特徴量と共に使用できますが、この記事では視覚化を容易にするために2次元に制限します。

次の図を生成します。

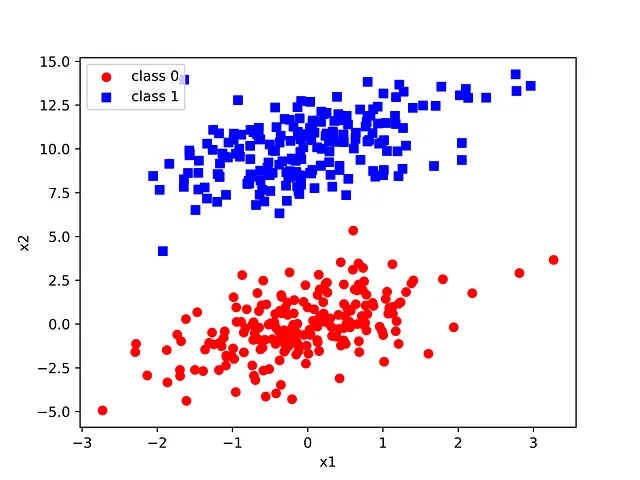
2つのガウス分布は、適切な平均値と共分散を選択することで意図的に引き伸ばされ、遠くに配置されています。後でこれに戻ります。

パーセプトロンの実装と使用

パーセプトロンの実装は以下のようになります。モデルを初期化し、フィットさせ、最後に予測を実行します。

初期化メソッドでは、学習率、最大反復回数、再現性のための乱数生成器のシードを設定します。fitメソッドでは、一様分布からサンプリングされた小さな数値で重みを設定するために乱数生成器が作成され、バイアスはゼロに初期化されます。それから、最大エポック回数のために反復します。各エポックでは、誤分類の数を数えることで収束を監視し、可能であれば早期終了します。誤分類されたサンプルごとに重みとバイアスを前述のセクションで説明したように更新します。誤分類の数がゼロの場合、改善の余地がないため、次のエポックの継続は不要です。predictメソッドは、重みと特徴量のドット積を計算し、バイアスを加え、ステップ関数を適用するだけです。

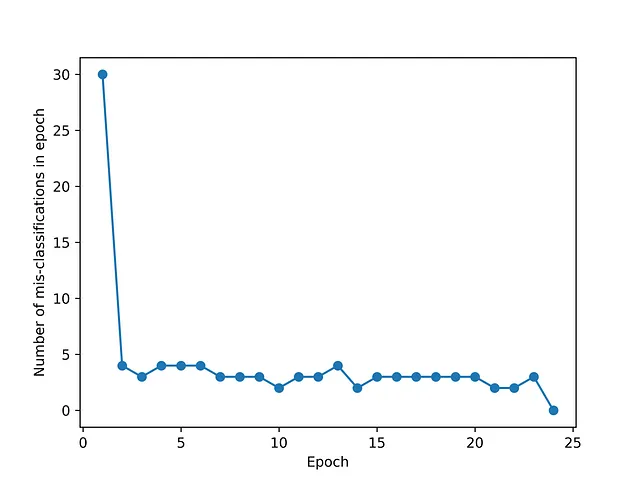
上記のパーセプトロンクラスを合成データセットで使用すると、収束は24エポックで達成され、指定された最大エポック数を使い果たす必要はありませんでした

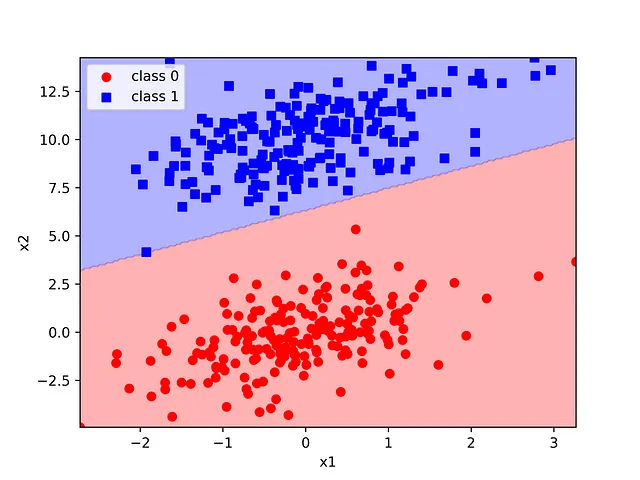
決定境界は、scikit-learnの決定境界ユーティリティ関数を使用して簡単に可視化できます。この関数を使用するには、トレーニングセットの特徴値範囲をスパンする200×200のポイントグリッドを生成します。基本的には、予測されたクラスによるコンタープロットを構築し、サンプルを散布図としてオーバーレイし、真のラベルを使用して色付けします。この方法は決定境界のプロット方法として非常に汎用的であり、任意の2次元の分類器で役立ちます。

2つの合成ガウス分布は、数行のコードでスクラッチから作成できるモデルを使用して完全に分離されました。この方法の単純さとエレガンスは、機械学習の優れた導入的かつ動機付けの例となります。

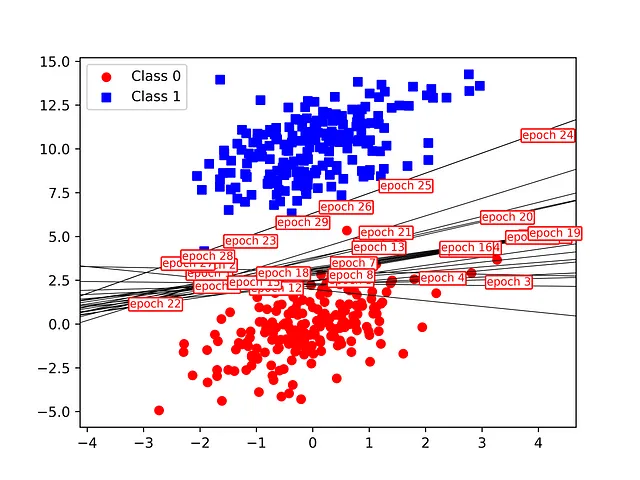
モデルのフィッティングプロセスを途中で停止することで、異なるエポックでの決定境界の進化を視覚化することもできます。これは、最大エポック数の増加するカットオフを使用してモデルをフィットすることで実現できます。すべての試行では、フィットされた（おそらく収束していない）モデルの重みとバイアスを使用し、決定境界を線としてプロットします。線はエポック番号で注釈が付けられます。これは、ウォームスタートを使用してより洗練された方法で実装される可能性がありますが、モデルのフィッティングは非常に速く、追加の複雑さはそれに値しません。

異なるエポックの決定境界の進化は、以下の図に示されています。最初に、少数のクラス0のサンプルが誤分類され、これにより決定境界線の傾きと切片が徐々に変化します。収束は24エポックで達成されたことが、上記の収束図と一致していることがわかります。決定境界がクラスを完全に分離するまでフィッティングが停止しますが、境界が周囲のサンプルにどれだけ近いかは関係ありません。

注意事項がいくつかあります。パーセプトロンの収束は確実ではなく、このために最大イテレーション数を設定することが重要です。実際に、線形分離可能なクラスに対しては数学的に収束が保証されることが証明されています。クラスが線形的に分離できない場合、重みとバイアスは最大イテレーション数に達するまで更新され続けます。これが、合成データセットでの2つのガウス分布がより離れた位置に移動された理由です。

もう1つの重要な注意点は、パーセプトロンには一意の解が存在しないということです。通常、線形分離可能なクラスを分離できる無数のハイパープレーンがあり、モデルはそれらの1つにランダムに収束します。これはまた、決定境界からの距離を測定することは確定的ではなく、したがってあまり有用ではないことを意味します。サポートベクターマシンはこの制限に対処しています。

パーセプトロンは基本的には単層のニューラルネットワークです。それがどのように機能するかを理解することは、非線形の問題に使用できる多層ニューラルネットワークとバックプロパゲーションアルゴリズムに飛ぶ前に役立ちます。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!