NumPyを使用したゼロからの線形回帰

NumPyを使った線形回帰

 

動機

 

線形回帰は機械学習における最も基本的なツールの一つです。データによくフィットする直線を見つけるために使用されます。単純な直線のパターンにのみ対応できるものの、その背後にある数学を理解することで、勾配降下法や損失最小化法についても理解することができます。これらは機械学習やディープラーニングのタスクで使用されるより複雑なモデルにおいて重要です。

• アリババグループによるこの論文では、FederatedScope-LLMという包括的なパッケージが紹介されていますこれは、フェデレーテッドラーニングでLLMを微調整するためのものです
• 「LangChain、Activeloop、そしてGPT-4を使用して、Redditのソースコードをリバースエンジニアリングするための分かりやすいガイド」
• コンテンツクリエーターに必要不可欠なChatGPTプラグイン

この記事では、NumPyを使用して線形回帰を基礎から構築します。Scikit-Learnなどの抽象的な実装ではなく、基礎から始めます。

 

データセット

 

Scikit-Learnのメソッドを使用して、ダミーデータセットを生成します。今のところ単一の変数のみを使用しますが、実装は任意の数の特徴量に対してトレーニングできる一般的なものとなります。

Scikit-Learnのmake_regressionメソッドは、ランダムな線形回帰のデータセットを生成し、ガウスノイズを追加してランダム性を持たせます。

X, y = datasets.make_regression(
        n_samples=500, n_features=1, noise=15, random_state=4)

 

500個のランダムな値を生成し、それぞれの値には1つの特徴量が対応しています。したがって、Xの形状は(500, 1)であり、500個の独立したXの値は、それぞれ対応するyの値を持っています。したがって、yの形状も(500, )です。

可視化すると、データセットは以下のようになります:

   

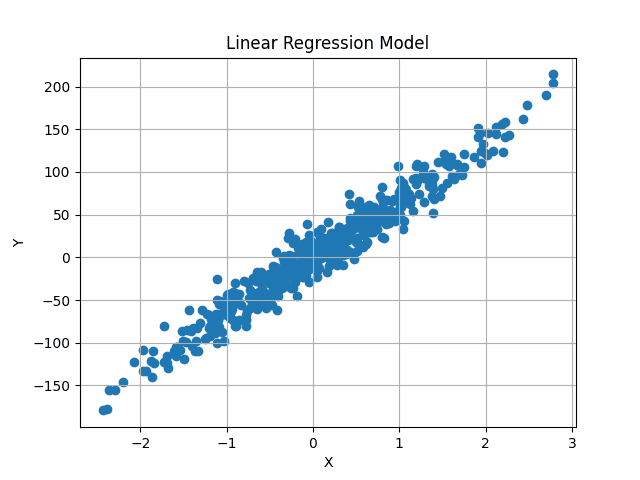
このデータの中心を通る最適な適合直線を見つけ、予測値と実際のy値の平均差を最小化することを目指します。

 

直感

 

線形直線の一般的な方程式は次のとおりです:

y = m*X + b

Xは数値で単一の値です。ここで、mとbは勾配とy切片（またはバイアス）を表します。これらは未知の値であり、これらの異なる値によって異なる直線が生成されます。機械学習では、Xはデータに依存し、yの値も同様です。 私たちはmとbのみを制御できるため、これらが私たちのモデルパラメータとなります。 この2つのパラメータの最適な値を見つけることを目指し、予測値と実際のy値の差を最小化する直線を生成します。

これは、Xが多次元の場合にも適用されます。その場合、mの数はデータの次元数と同じになります。たとえば、データに3つの異なる特徴量がある場合、3つの異なるm値（重みと呼ばれる）があります。

方程式は次のようになります:

y = w1*X1 + w2*X2 + w3*X3 + b

これは任意の数の特徴量に拡張できます。

しかし、バイアスと重みの最適な値をどのように知ることができるのでしょうか？実際には分かりません。しかし、勾配降下法を使用して反復的に最適な値を求めることができます。ランダムな値から始めて、複数のステップで少しずつ変更して最適な値に近づくまで繰り返します。

まずは、線形回帰を初期化し、最適化プロセスについて詳しく見ていきましょう。

 

線形回帰クラスの初期化

 

import numpy as np


class LinearRegression:
    def __init__(self, lr: int = 0.01, n_iters: int = 1000) -> None:
        self.lr = lr
        self.n_iters = n_iters
        self.weights = None
        self.bias = None

 

学習率と反復回数のハイパーパラメータを使用し、後で説明します。重みとバイアスは、データ内の入力特徴量の数に依存するため、現時点ではデータにアクセスできないため、Noneに設定されます。

 

フィットメソッド

 

フィットメソッドでは、データとそれに関連する値が提供されます。これらを使用して重みを初期化し、その後、モデルをトレーニングして最適な重みを見つけることができます。

def fit(self, X, y):
        num_samples, num_features = X.shape     # Xの形状[N、f]
        self.weights = np.random.rand(num_features)  # Wの形状[f、1]
        self.bias = 0

 

独立した特徴量Xは、形状が(num_samples、num_features)のNumPy配列です。この場合、Xの形状は(500、1)です。データの各行には対応するターゲット値がありますので、yも形状が(500、)または(num_samples)です。

この情報を抽出し、入力特徴量の数に基づいて重みをランダムに初期化します。したがって、重みも形状が(num_features、)のNumPy配列です。バイアスはゼロで初期化される単一の値です。

 

Y値の予測

 

上記で説明した直線の方程式を使用して予測されたy値を計算します。ただし、すべての値を合計するための反復的なアプローチではなく、より高速な計算のためにベクトル化アプローチを使用することができます。重みとXの値がNumPy配列であるため、行列の乗算を使用して予測を取得できます。

Xの形状は(num_samples、num_features)で、重みの形状は(num_features、)です。予測値は元のy値と一致する形状(num_samples、)であることを目指します。したがって、Xと重みを乗算するか、(num_samples、num_features) x (num_features、)を行って形状が(num_samples、)の予測値を得ることができます。

予測の最後にはバイアス値が加えられます。これは単一の行で簡単に実装できます。

# y_predの形状はN, 1にする必要があります
y_pred = np.dot(X, self.weights) + self.bias

 

ただし、これらの予測値は正しいですか？明らかに違います。重みとバイアスの初期値はランダムに設定されているため、予測値もランダムになります。

最適な値をどのように取得するのでしょうか？勾配降下法。

 

損失関数と勾配降下法

 

予測されたy値と目標のy値の両方を持っているため、両者の差を求めることができます。平均二乗誤差（MSE）は実数値の比較に使用されます。方程式は次のようになります:

   

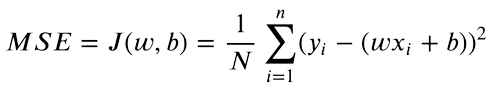
値の絶対的な差のみに興味があります。予測値が元の値よりも高い場合と低い場合は同じくらい悪いです。したがって、予測値と目標値の差を2乗し、負の差を正に変換します。さらに、これにより目標と予測の間の大きな差が罰則化され、より高い差の二乗が最終的な損失により多く貢献します。

予測が可能な限り元の目標に近づくために、この関数を最小化しようとします。損失関数は勾配がゼロの場所で最小になります。重みとバイアスの値のみを最適化できるため、MSE関数の重みとバイアスの値に対する偏微分を取ります。

   

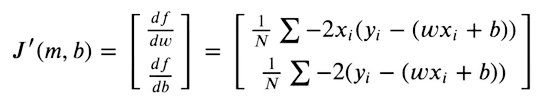
その後、勾配の値を利用して重みを最適化します。これには勾配降下法を使用します。

   

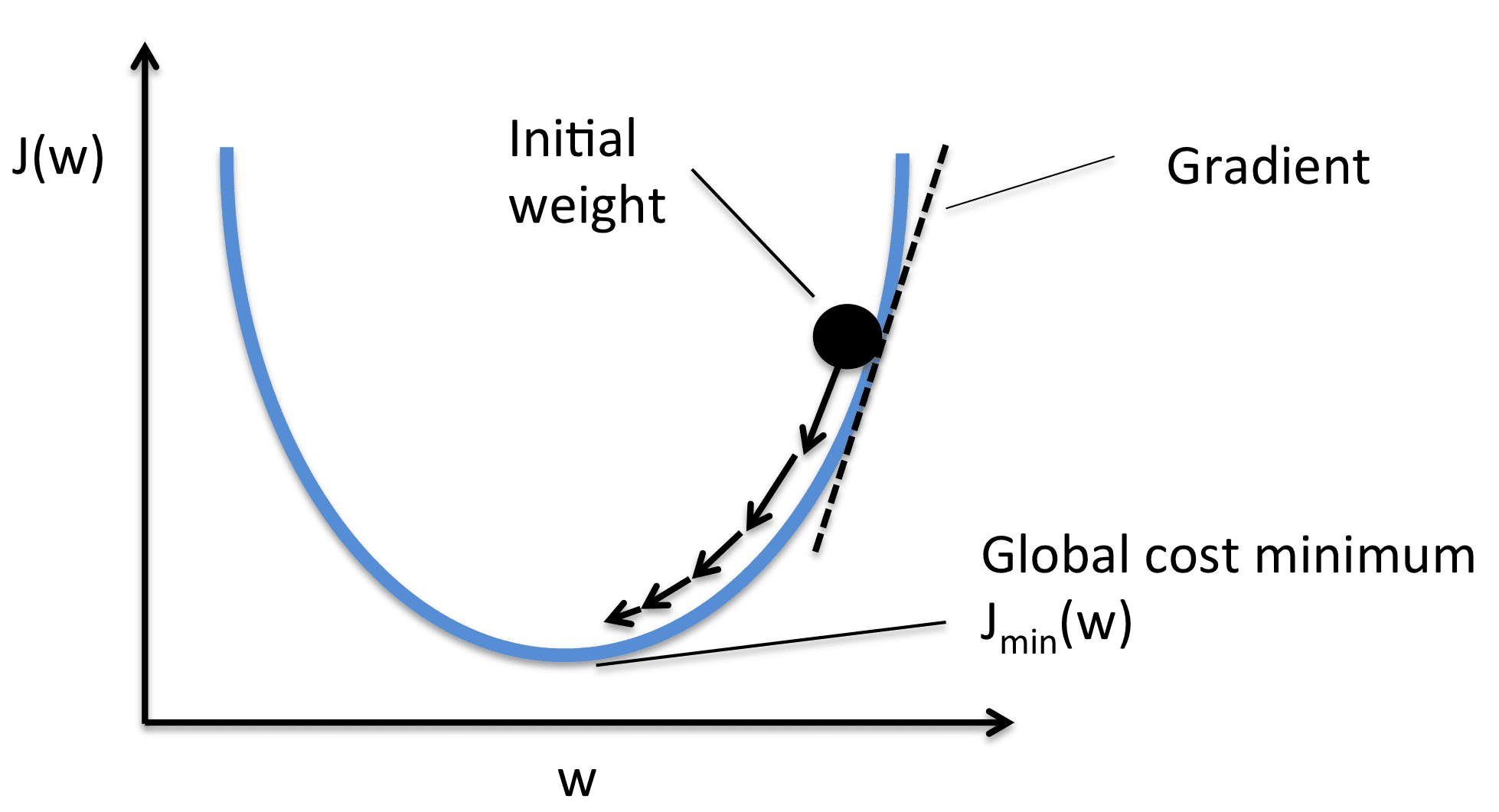
各重み値に関する勾配を取り、それらを勾配の反対側に移動させます。これにより、損失は最小値に向かって押されます。画像のように、勾配が正の場合は重みを減らします。これにより、J(W)または損失が最小値に向かいます。したがって、最適化の方程式は次のようになります:

   

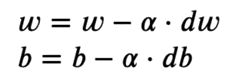
学習率（またはα）は画像に示されているような増分ステップを制御します。値をわずかに変更するだけで、最小値に向かうための安定した移動を行います。

 

実装

 

基本的な代数的操作を使用して導関数の方程式を簡略化すると、非常に簡単に実装できます。

   

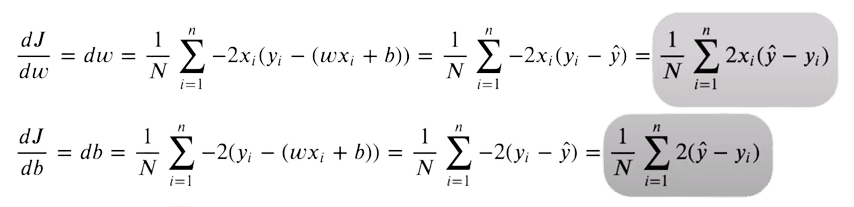
微分については、次の2行のコードを使用して実装します：

# X -> [ N, f ]
# y_pred -> [ N ]
# dw -> [ f ]
dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
db = (1 / num_samples) * np.sum(y_pred - y)

 

dwの形状は再び(num_features, )です。したがって、各重みに対して個別の微分値があります。それらは個別に最適化されます。dbには単一の値があります。

これらの値を最適化するために、基本的な減算を使用して勾配の逆方向に移動させます。

self.weights = self.weights - self.lr * dw
self.bias = self.bias - self.lr * db

 

これもまた、単一のステップのみです。ランダムに初期化された値にわずかな変更を加えるだけです。これらの手順を繰り返し実行して、最小値に収束します。

完全なループは次のとおりです：

for i in range(self.n_iters):

            # y_predの形状はN, 1である必要があります
            y_pred = np.dot(X, self.weights) + self.bias

            # X -> [N,f]
            # y_pred -> [N]
            # dw -> [f]
            dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
            db = (1 / num_samples) * np.sum(y_pred - y)

            self.weights = self.weights - self.lr * dw
            self.bias = self.bias - self.lr * db

 

予測

 

トレーニング中と同じ方法で予測します。ただし、現在は最適な重みとバイアスのセットがあります。予測値は元の値に近くなるはずです。

def predict(self, X):
        return np.dot(X, self.weights) + self.bias

 

結果

 

ランダムに初期化された重みとバイアスで、予測は次のようになりました：

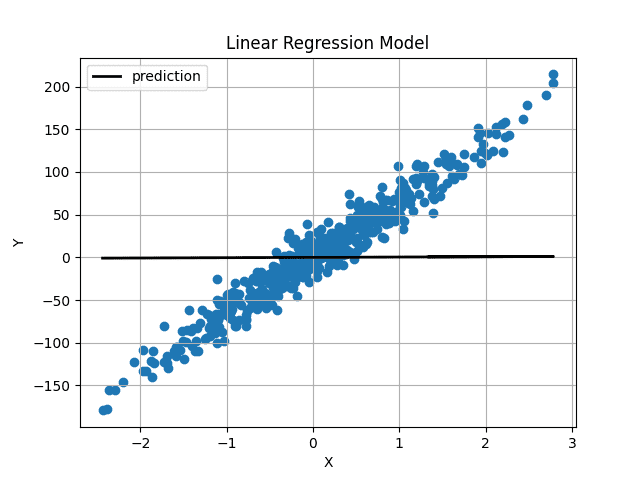  Image by Author   重みとバイアスは0に非常に近く初期化されているため、水平な直線が得られます。1000回の反復の後、以下のようになります：

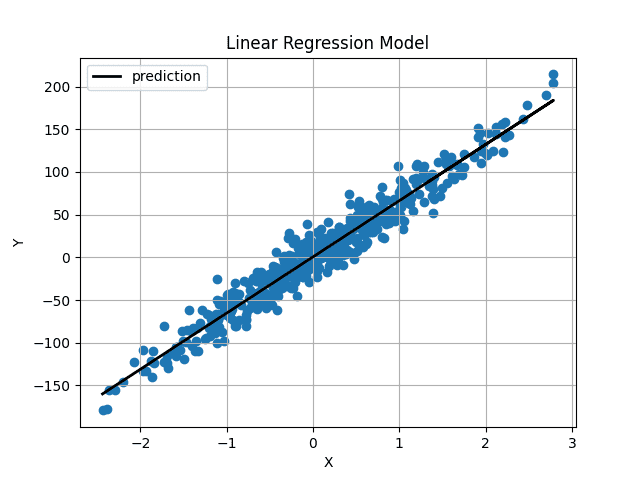  Image by Author  

予測された直線はデータの中心を通り、最適な適合直線のように見えます。 

 

結論

 

これで線形回帰をゼロから実装しました。完全なコードはGitHubでも利用できます。

import numpy as np


class LinearRegression:
    def __init__(self, lr: int = 0.01, n_iters: int = 1000) -> None:
        self.lr = lr
        self.n_iters = n_iters
        self.weights = None
        self.bias = None

    def fit(self, X, y):
        num_samples, num_features = X.shape     # Xの形状は[N, f]です
        self.weights = np.random.rand(num_features)  # Wの形状は[f, 1]です
        self.bias = 0

        for i in range(self.n_iters):

            # y_predの形状はN, 1である必要があります
            y_pred = np.dot(X, self.weights) + self.bias

            # X -> [N,f]
            # y_pred -> [N]
            # dw -> [f]
            dw = (1 / num_samples) * np.dot(X.T, y_pred - y)
            db = (1 / num_samples) * np.sum(y_pred - y)

            self.weights = self.weights - self.lr * dw
            self.bias = self.bias - self.lr * db

        return self

    def predict(self, X):
        return np.dot(X, self.weights) + self.bias

    Muhammad Arhamは、コンピュータビジョンと自然言語処理の分野で働くディープラーニングエンジニアです。彼はVyro.AIでグローバルなトップチャートに達したいくつかの生成AIアプリケーションの展開と最適化に取り組んできました。彼は知的システム向けの機械学習モデルの構築と最適化に興味を持ち、継続的な改善を信じています。  

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!