マルチアームバンディットを用いた動的価格設定:実践による学習
Multi-armed bandit for dynamic pricing Learning through practice
リアルワールドの使用事例に強化学習戦略を適用すると、特にダイナミックプライシングにおいて多くの驚きが明らかになることがあります
ダイナミックプライシング、強化学習、そしてマルチアームバンディット
意思決定の問題の広大な世界で、一つのジレンマが特に強化学習戦略によって所有されています:探索と活用の対立です。スロットマシン(別名「ワンアームバンディット」)が並ぶカジノに入ったと想像してください。各マシンは異なる、未知の報酬を支払います。最高の配当を持つマシンを見つけるために、各マシンを探索して遊ぶのか、それともジャックポットだと期待して一つのマシンに固執するのか。この比喩的なシナリオは、マルチアームバンディット(MAB)問題の基本を成しています。目標は、一連のプレイで報酬を最大化する戦略を見つけることです。探索は新しい洞察を提供しますが、活用は既に持っている情報を利用します。
さて、この原則を小売業のダイナミックプライシングに移します。新しい商品を持つECストアのオーナーであると仮定しましょう。最適な販売価格については確信がありません。収益を最大化する価格をどのように設定しますか?顧客の支払い意思を理解するために異なる価格を試すべきか、過去に好調だった価格を活用すべきか?ダイナミックプライシングは、見かけ上のMAB問題です。各時間ステップでは、各候補価格点はスロットマシンの「アーム」と見なされ、その価格から生成される収益が「報酬」となります。別の見方をすれば、ダイナミックプライシングの目的は、顧客の需要が異なる価格点にどのように反応するかを迅速かつ正確に測定することです。より簡単に言えば、顧客の行動を最もよく反映する需要曲線を特定することです。
この記事では、よく定義された(しかし直感的でない)需要曲線に対する4つのマルチアームバンディットアルゴリズムを探求します。そして、各アルゴリズムの主な強みと制限を分析し、パフォーマンスを評価するための主要な指標について探究します。
需要曲線のモデリング
伝統的に、経済学における需要曲線は、製品の価格と消費者が購入する数量との関係を説明しています。一般的に、価格が上昇すると需要は通常減少する傾向があるため、曲線は下方に傾斜します。人気のある製品であるスマートフォンやコンサートチケットなどを考えてみてください。価格が下げられると、より多くの人々が購入する傾向がありますが、価格が急上昇すると、熱心なファンでも二度考えるかもしれません。
しかし、私たちの文脈では、需要曲線を少し異なる方法でモデル化します:価格に対する確率を対比します。なぜなら、特にデジタル商品やサービスのダイナミックプライシングの場合、与えられた価格での販売の可能性を考える方が、正確な数量について推測するよりも意味があるからです。このような環境では、各価格試行は、成功(または購入)の確率の探索として見なすことができます。それは、与えられたテスト価格に依存する確率pを持つベルヌーイ確率変数として簡単にモデル化できます。
ここで特に興味深いことが起こります:直感的には、マルチアームバンディットアルゴリズムの課題は、購入確率が最も高い理想的な価格を見つけ出すことだと思われるかもしれませんが、それはそれほど単純ではありません。実際には、私たちの最終目標は収益(または利益)を最大化することです。これは、最も多くの人々が「購入」をクリックする価格を探しているわけではなく、関連する購入確率と乗算したときに最も高い期待収益をもたらす価格を探していることを意味します。例えば、収益が大きいが購入者が少ない高い価格を設定することができます。一方、非常に低い価格はより多くの購入者を引きつけるかもしれませんが、総収益は高い価格のシナリオよりも低いかもしれません。したがって、私たちの文脈では、「需要曲線」について話すことはやや異例です。私たちの目標曲線は、需要そのものではなく、主に購入確率を表します。
さて、数学に移りましょう。価格感度を扱う場合、特に消費者の行動は常に線形ではありません。線形モデルは、価格の増加ごとに需要が一定の減少を示唆するかもしれませんが、実際にはこの関係はより複雑で非線形です。この行動をモデル化する方法の一つは、この微妙な関係をより効果的に捉えることができるロジスティック関数を使用することです。私たちが選んだ需要曲線のモデルは次のようになります:
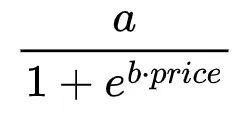
ここでは、aは購入の最大可能性を示し、bは価格変動に対する需要曲線の感度を調整します。bの値が高いほど、より急な曲線であり、価格が上がるにつれて購入確率がより急速に低下します。
任意の価格点に対して、関連する購入確率pを取得できます。次に、pをベルヌーイ乱数生成器に入力して、特定の価格提案に対する顧客の反応をシミュレートすることができます。言い換えれば、価格が与えられた場合、報酬関数を簡単にエミュレートできます。
次に、この関数を価格で乗算して、特定の価格点の期待収益を得ることができます:
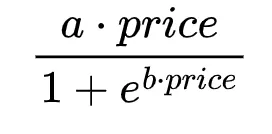
予想通り、この関数は最大確率に対応する場所で最大値に達しません。また、最大値に関連する価格はパラメータaの値に依存しませんが、最大期待収益は依存します。
微積分の知識を思い出すと、期待収益の導関数の式を導くこともできます(積の法則と連鎖律の組み合わせを使用する必要があります)。それはまさにリラックスできる練習ではありませんが、あまり難しいものではありません。以下は期待収益の導関数の解析的な表現です:
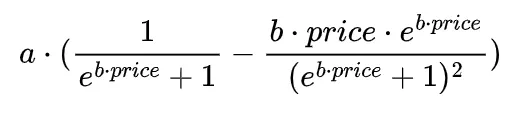
この導関数により、期待収益曲線を最大化する正確な価格を見つけることができます。言い換えれば、この特定の式を数値アルゴリズムと組み合わせて使用することで、期待収益を最大化する価格を簡単に決定することができます。
そして、これが必要なものです。aとbの値を固定することで、バンディットが見つける必要のある目標価格をすぐに知ることができます。これをPythonでコーディングするのは、わずか数行のコードの問題です:
私たちのユースケースでは、a = 2、b = 0.042と設定し、目標価格は約30.44で、最適確率は0.436です(→最適平均報酬は30.44 * 0.436 = 13.26)。この価格は一般的には明らかになっておらず、これが私たちのマルチアームバンディットアルゴリズムが探す価格です。
マルチアームバンディット戦略
目標を特定したので、パフォーマンス、強み、弱みをテストおよび分析するためのさまざまな戦略を探索する時が来ました。MABの文献にはいくつかのアルゴリズムが存在しますが、実世界のシナリオでは、4つの主要な戦略(およびそのバリエーション)が主にバックボーンを形成しています。このセクションでは、これらの戦略の概要を簡単に説明します。読者はそれらについて基本的な理解を持っていることを前提としていますが、より詳細な探求を希望する方には、記事の最後に参考文献が提供されています。各アルゴリズムを紹介した後、そのPython実装も示します。各アルゴリズムは固有の一連のパラメータを持っていますが、すべてのアルゴリズムは共通の重要な入力であるarm_avg_rewardベクトルを使用します。このベクトルは、現在の時刻tまでの各アーム(またはアクション/価格)から得られた平均報酬を示しています。この重要な入力は、すべてのアルゴリズムが次の価格設定についての情報を持った意思決定を行うのに役立ちます。
私が動的価格設定の問題に適用するアルゴリズムは次のとおりです:
グリーディ:この戦略は、最初の数回のプレイで最も多くのコインを与えたマシンに常に戻るようなものです。各マシンを少し試した後、最も良さそうなマシンに固執します。ただし、問題が発生する可能性があります。そのマシンが最初に運が良かっただけかもしれません。グリーディ戦略は、より良い選択肢を見逃すかもしれません。明るい面では、コードの実装は非常にシンプルです:
初期シナリオ(すべての報酬が0の場合)と通常のシナリオを区別することは重要です。通常、実装されているのは「else」の部分だけであり、すべての報酬が0の場合でも機能します。しかし、このアプローチは最初の要素にバイアスを持つ可能性があります。この見落としをすると、最適な報酬が最初のアームに関連付けられている場合に特にそのバイアスを支払うことになるかもしれません(はい、私もそうでした)。グリーディーなアプローチは通常、最も性能が低いものであり、パフォーマンスのベースラインとして主に使用されます。
ϵ-グリーディー:ε-グリーディー(イプシロン-グリーディー)アルゴリズムは、グリーディーなアプローチの主な欠点に対処するための修正です。これは、通常は小さな値である確率ε(イプシロン)を導入し、ランダムなアームを選択することで探索を促進します。確率1−εで、最も推定された報酬を持つアームを選択し、利用を促進します。ランダムな探索と既知の報酬の利用のバランスを取ることで、ε-グリーディー戦略は純粋なグリーディーな方法と比較して、より良い長期的なリターンを目指します。実装は簡単で、グリーディーのコードの上に追加の「if」文を配置するだけです。
UCB1(上限信頼区間):UCB1戦略は、新しい街で最高のレストランを見つけようとする好奇心旺盛な探検家のようなものです。彼らが楽しんだお気に入りの場所がある一方で、より良い場所を見つける可能性の魅力は日を追うごとに高まります。私たちの文脈では、UCB1は既知の価格ポイントの報酬と未知のものの不確実性を組み合わせます。数学的には、このバランスは、価格ポイントの平均報酬に、最後に試されてからどれくらい経過したかに基づく「不確実性ボーナス」を加えることで達成されます。このボーナスは次のように計算されます:
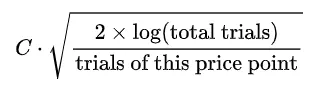
これは未試験価格に対する「成長する好奇心」を表しています。ハイパーパラメータCは、利用と探索のバランスを制御し、Cの値が高いほど、サンプリングされていないアームの探索が増えます。既知の報酬と好奇心ボーナスの組み合わせで常に最も高い価格を選択することにより、UCB1は既知のものに固執しつつ、未知のものにも進出し、最大の収益のための最適な価格ポイントを明らかにしようとします。このアプローチの正しい実装から始めますが、少し調整する必要があることもすぐにわかるでしょう。
トンプソンサンプリング:このベイズアプローチは、事後報酬分布に基づいて確率的にアームを選択することで、探索と利用のジレンマに対処します。これらの報酬が成功/失敗などの2値の結果を表すベルヌーイ分布に従う場合、トンプソンサンプリング(TS)は共役事前分布としてベータ分布を使用します(参考のためにこの表を参照してください)。各アームに対して非情報的なベータ(1,1)事前分布で初期化し、アルゴリズムは報酬を観測することで分布のパラメータを更新します。成功するとアルファパラメータが増加し、失敗するとベータが増加します。各プレイでは、TSは各アームの現在のベータ分布から抽出し、最も高いサンプル値を選択します。この方法論により、TSは収集された報酬に基づいて動的に調整し、不確実なアームの探索と報酬が得られることがわかっているアームの利用を巧みにバランスさせることができます。私たちの具体的なシナリオでは、基本的な報酬関数がベルヌーイ分布に従う(購入の場合は1、購入しない場合は0)が、実際の関心のある報酬は、この基本報酬と現在のテスト中の価格の積です。したがって、TSの実装にはわずかな変更が必要です(これにより、いくつかの驚きも導入されます)。
変更は実際には非常にシンプルです:事後推定から抽出されたサンプルは、それぞれの価格ポイントと乗算されます(行3)。この変更により、意図される平均収益に基づいて意思決定が行われるため、最も高い購入確率に焦点を当てることから移行します。
結果を評価する方法は?
この時点で、動的価格設定の文脈で4つのアルゴリズムのパフォーマンスを比較するシミュレーションを構築するためのすべての主要な要素を収集したので、自分自身に問いかける必要があります:具体的には何を測定するのでしょうか?選択するメトリックは重要であり、アルゴリズムの実装を比較および改善するプロセスを導く役割を果たします。この試みでは、次の3つの主要な指標に焦点を当てています:
- 後悔:このメトリックは、選択されたアクションによって得られた報酬と最良のアクションによって得られた報酬との差を測定します。数学的には、時間tにおける後悔は次のようになります:後悔(t)=最適報酬(t)−実際の報酬(t)。時間の経過とともに蓄積される後悔は、最適なシナリオに比べてアルゴリズムのパフォーマンスを明確に示すため、累積報酬よりも好まれます。理想的には、後悔値が0に近い場合、最適な意思決定に近いことを示します。
- 反応性:このメトリックは、アルゴリズムが目標の平均報酬にどれだけ速く近づくかを測定します。基本的には、アルゴリズムの適応性と学習効率の尺度です。アルゴリズムが望ましい平均報酬を迅速に達成できるほど、より反応性が高くなり、最適な価格ポイントへの迅速な調整を意味します。私たちの場合、目標報酬は最適な平均報酬の95%であり、13.26です。ただし、初期のステップでは高い変動性が見られる場合があります。たとえば、幸運な初期の選択により、低い確率のアームが高い価格に関連付けられた成功をもたらし、すぐにしきい値を達成することができます。そのような変動のため、私はより厳密な反応性の定義を採用しました:初期の100ステップを除いて、10
シミュレーションの実行
MABアルゴリズムの評価は、その結果の高度に確率的な性質により困難を伴います。これは、数量の決定に固有のランダム性により、結果が実行ごとに大きく異なる可能性があることを意味します。堅牢な評価のためには、対象のシミュレーションを複数回実行し、各シミュレーションから結果とメトリクスを蓄積し、その平均値を計算することが最も効果的なアプローチです。
最初のステップは、意思決定プロセスをシミュレートする関数を作成することです。この関数は、以下の画像で表されるフィードバックループを実装します。
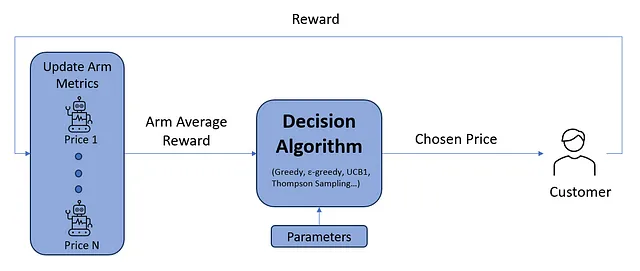
これがシミュレーションループの実装です:
この関数への入力は次のとおりです:
prices: テストしたい候補価格のリスト(基本的には「アーム」と呼ばれます)。nstep: シミュレーションの合計ステップ数。strategy: 次の価格に関する意思決定を行うためにテストするアルゴリズム。
最後に、外側のループのためのコードを書く必要があります。このループでは、対象の戦略ごとに
run_simulationを複数回呼び出し、各実行からの結果を収集し集計し、その結果を表示します。分析には、以下の設定パラメータを使用します:
prices: 価格候補 → [20, 30, 40, 50, 60]nstep: 各シミュレーションの時間ステップ数 → 10000nepoch: シミュレーションの実行回数 → 1000
さらに、価格候補を設定することで、関連する購入確率を迅速に取得できます。これらの確率は、(おおよそ) [0.60, 0.44, 0.31, 0.22, 0.15] です。
結果
シミュレーションを実行した後、いくつかの結果を確認できるようになりました。まず、累積リグレットのプロットから始めましょう:
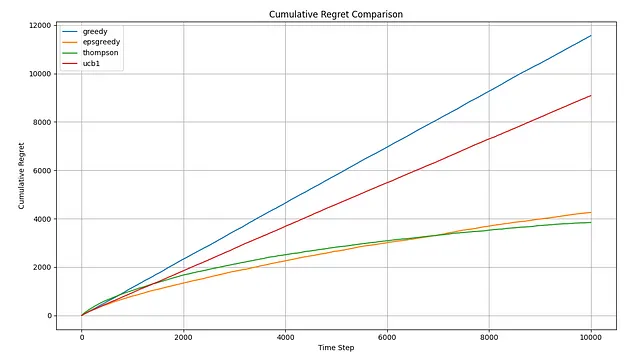
グラフからわかるように、平均累積リグレットの点でTSが勝者ですが、ε-greedyを上回るには約7,500ステップかかります。一方、UCB1は明らかな敗者です。基本的な構成では、貪欲なアプローチとほぼ同等のパフォーマンスを発揮します(後で詳しく説明します)。他の利用可能なメトリクスを探索することで、結果をより良く理解しましょう。4つの場合すべてで、リアクティビティは非常に大きな標準偏差を示しているため、外れ値に強く耐性を持つ中央値に焦点を当てます。
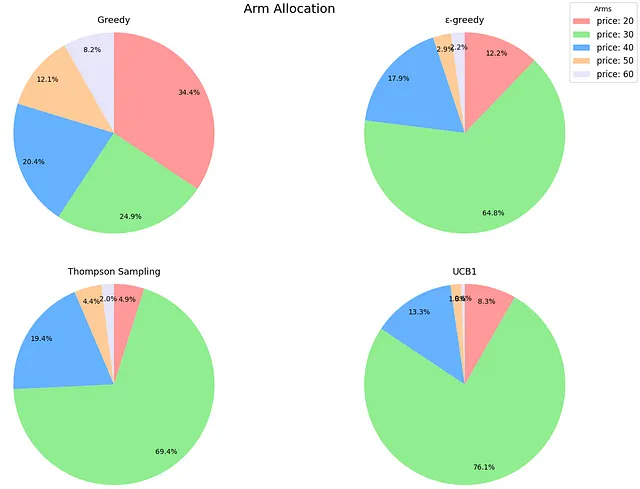
プロットからの初期の観察結果は、平均値ではTSがε-greedyを上回る一方、中央値ではわずかに遅れていることです。ただし、その標準偏差は小さいです。特に興味深いのは、リアクティビティの棒グラフで、TSが迅速な平均報酬の達成に苦労していることが示されています。最初は直感に反していましたが、このシナリオでのTSのメカニズムが問題を明確にしました。先ほど述べたように、TSは購入確率を推定します。しかし、決定はこれらの確率と価格の積に基づいて行われます。実際の確率(つまり、[0.60、0.44、0.31、0.22、0.15])を知っていることにより、TSが積極的にナビゲートしている期待報酬を計算することができます:[12.06、13.25、12.56、10.90、8.93]。本質的には、基になる確率がかなり異なるにもかかわらず、期待される収益値はその視点から比較的近いです、特に最適価格に近い場合です。これは、TSがこの文脈で最適なアームを識別するためにより多くの時間を要することを意味します。TSは最も優れたアルゴリズムであり続けます(シミュレーションを延長すれば、その中央値はε-greedyのそれを下回るようになります)、しかし、このコンテキストでは最良の戦略を特定するためにより長い期間を要します。以下は、アームの割り当ての円グラフで、TSとε-greedyが最良のアーム(価格=30)を非常にうまく識別し、シミュレーション中にそれをほとんどの時間使用していることが示されています。
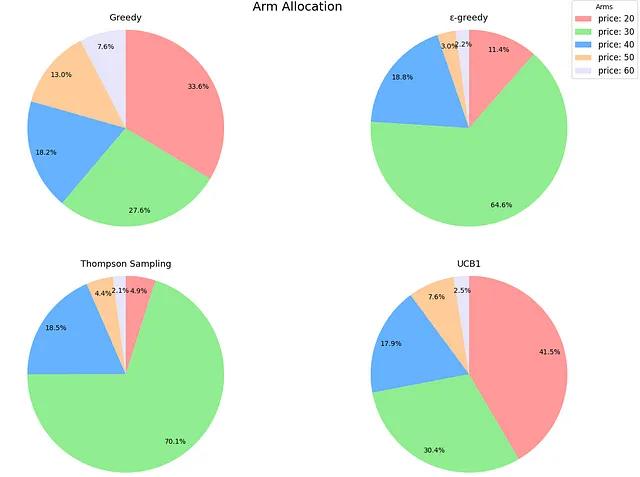
さて、UCB1に戻りましょう。後悔と反応性は、UCB1が基本的に完全な探索的アルゴリズムとして機能していることを確認しています。平均報酬のレベルを早く得る一方で、後悔が大きく、結果の変動性が高いです。アームの割り当てを見てみると、それはさらに明確になります。UCB1は、期待される報酬が高い3つのアーム(価格20、30、40)に重点を置いているため、グリーディなアプローチよりわずかに賢いですが、実質的には全く探索しません。
ハイパーパラメータのチューニングを導入します。探索と利用のバランスを取る重みCの最適な値を決定する必要があることは明らかです。最初のステップは、UCB1のコードを修正することです。
この更新されたコードでは、ハイパーパラメータCで重み付けされた「不確実性ボーナス」を追加する前に平均報酬を正規化するオプションを組み込んでいます。これは、最適なハイパーパラメータの一貫した検索範囲(0.5〜1.5など)を許すためのものです。この正規化を行わないと、同様の結果を得ることはできますが、検索間隔は毎回取り扱う値の範囲に基づいて調整する必要があります。最適なCの値を見つけるための退屈な作業は省略しますが、グリッドサーチを通じて簡単に決定できます。最適な値は0.7であることがわかりました。さあ、シミュレーションをやり直して結果を調べてみましょう。
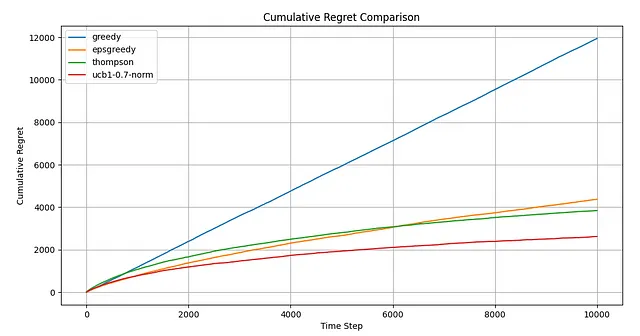
これはかなりの展開ですね。今や、UCB1が明らかに最も優れたアルゴリズムです。反応性の面でも、前のスコアと比べてわずかに悪化しているだけです。
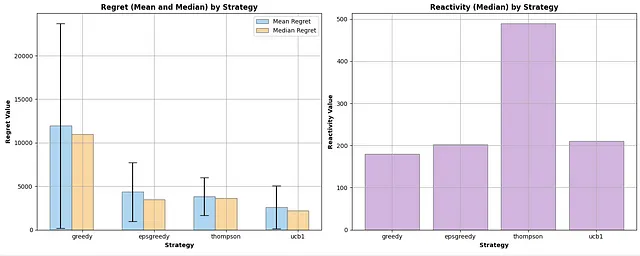
さらに、アームの割り当ての観点から見ると、UCB1が間違いなくリーダーになりました。
学んだことと次のステップ
- 理論 vs. 経験: 新しいトピックに取り組む際には、本に基づいた学習から始めることは必須の第一歩です。しかし、なる早く実践的な経験に身を置くことで、情報を知識に変換するスピードが速くなります。アルゴリズムを実際のユースケースに適用する際に遭遇するニュアンス、微妙さ、そしてコーナーケースは、読んだデータサイエンスの本以上の洞察を提供します。
- メトリクスとベンチマークを知る: 何をしているのかを測定できなければ、改善することはできません。どのメトリクスを使用するかを理解せずに実装を開始しないでください。後悔曲線のみを考慮した場合、「UCB1は機能しない」と結論づける可能性があります。特にアームの割り当てなどの他のメトリクスを評価することで、アルゴリズムが十分に探索していないことが明らかになりました。
- ワンサイズがすべてに合うわけではない: UCB1が分析で最も優れた選択肢として浮上したとしても、それは動的価格設定の課題に対する普遍的な解決策であることを意味しません。このシナリオでは、最適な値がわかっているため、チューニングは簡単でした。現実では、状況はそんなに明確ではありません。UCB1アルゴリズムの探索要素をテストして調整するための十分なドメイン知識や手段を持っていますか?もしかしたら、即座の結果を約束する信頼できる効果的なオプションであるε-greedyの方に傾くかもしれません。または、1時間に1万回製品を展示する賑やかな電子商取引プラットフォームを運営しており、Thompson Samplingが最大の累積報酬を最終的に達成すると確信して、忍耐強くなりたいかもしれません。そう、人生は簡単ではありません。
最後に、この分析が困難に見えた場合、残念ながら、これは非常に単純化された状況を既に表しています。現実世界の動的価格設定では、価格と購入確率は真空中に存在するのではなく、常に変化する環境に存在し、さまざまな要素に影響を受けます。たとえば、購入確率が年間を通じて、すべての顧客のデモグラフィックや地域全体で一貫している可能性は非常に低いです。言い換えれば、価格の最適な決定を最適化するためには、顧客の文脈を考慮する必要があります。この考慮は、次の記事の焦点となります。次の記事では、顧客情報を統合し、コンテキスト依存のバンディットアルゴリズムについて詳しく説明します。お楽しみに!
参考文献
- https://www.amazon.it/Reinforcement-Learning-Introduction-Richard-Sutton/dp/0262039249
- https://www.geeksforgeeks.org/epsilon-greedy-algorithm-in-reinforcement-learning/
- https://towardsdatascience.com/multi-armed-bandits-upper-confidence-bound-algorithms-with-python-code-a977728f0e2d
- https://towardsdatascience.com/thompson-sampling-fc28817eacb8
- https://www.youtube.com/watch?v=e3L4VocZnnQ
- https://www.youtube.com/watch?v=e3L4VocZnnQ
- https://www.youtube.com/watch?v=Zgwfw3bzSmQ&t=2s
この記事はお楽しみいただけましたでしょうか?AI、NLP、機械学習、データ分析の応用に興味がある場合、他の私の作品もお楽しみいただけるかと思います。私の目標は、これらの変革的な技術を実践的なシナリオで示す具体的な記事を作成することです。もし同じような方であれば、最新の記事についてはVoAGIでフォローしてください。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
- 「ビジョン・ランゲージの交差点でのブレイクスルー:オールシーイングプロジェクトの発表」
- 「大規模言語モデルのパディング — Llama 2を用いた例」
- 「オーディオソース分離のマスターキー:AudioSepを紹介して、あなたが説明するものを分離します」
- 「RBIは、規制監督のためにAIを活用するために、マッキンゼーとアクセンチュアと提携します」
- このAIの論文では、非英語の言語で事前学習されたLLMsを強化するために、言語間で意味の整合性を構築することを提案しています
- 「ステレオタイプやディスインフォメーションに対抗するAIヘイトスピーチ検出」
- 「Mozilla Common Voiceにおける音声言語認識 — 音声変換」





