「価格最適化の技術を習得する — データサイエンスのソリューション」
Mastering Price Optimization Technology - Data Science Solutions
リテールで価格最適化のための実世界のデータサイエンスソリューションの秘密を解き放つ

目次:
1. 概要 2. 弾力性モデリング 3. 最適化
1. 概要
価格はビジネスの世界において非常に重要な役割を果たしています。売上と利益のバランスをとることは、どのビジネスにおいても成功するために非常に重要です。それをデータサイエンスの方法でどのように実現できるのでしょうか?このセクションでは、価格最適化のための効果的なデータサイエンスソリューションの直感を構築し、その各コンポーネントの詳細とコードについて説明します。
注意:異なる種類の価格戦略が存在しますが、この記事では、価格変更履歴に十分なデータがある従来のビジネス/確立されたブランドの価格戦略に焦点を当てます。詳細に入る前に、基本的なアプローチを見てみましょう。
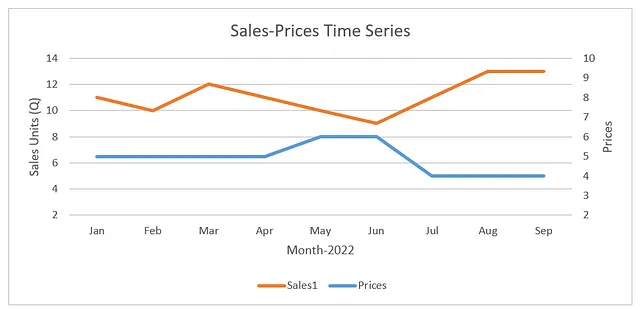
商品1の売上と価格をプロットしました。過去9か月間で2回の価格変更があり、明らかに売上への影響が見られます。価格が低いと売上が高くなります。では、過去の価格変更による売上への影響をどのように定量化し、将来の商品の最適価格を予測するのでしょうか。
Jan-Aprの興味深い観察結果として、価格は$5で固定されていましたが、売上の変動が観察されます。これは非常に正常なことで、実際の世界では季節性、休日、プロモーションイベント、マーケティング費用など、売上に影響を与える多くの外部要因が存在するからです。そのため、実際の売上ではなく、異なるモデルを使用して導出されるベースラインの売上をモデル化します。
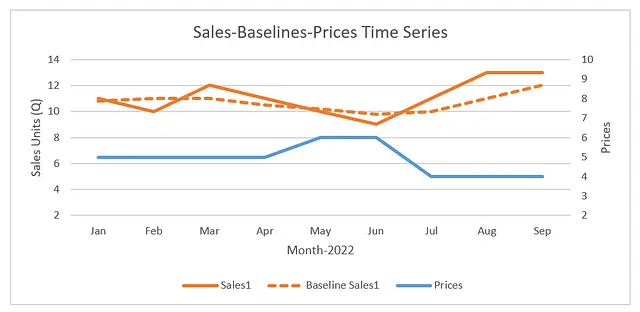
ベースラインの売上シリーズでは、売上のスムーズな傾向を観察できます。これは100%正確ですか?絶対にそうではありません!データサイエンスは、現実にどれだけ近づけることができるかについてのものです。では、プロセスに移りましょう。
例えば、Retailmartグループのさまざまな店舗の数千の商品の価格を提供するように雇われたとします。同じ商品の価格は異なる店舗ごとに異なる場合があります。会社は過去5年間のデータを提供しています。この問題を解決するためのアプローチはどうすればよいでしょうか?
価格メーターの例で理解しましょう。価格メーターがあり、最小値と最大値が固定され、ダイヤルはこれらの2つの極端な値の間で移動できるとします。現在の価格を指すようにダイヤルが指しているとします。私たちの目的は、利益を最大化できる位置でダイヤルを止めることです。
ダイヤルを右に動かすと(つまり、価格を上げると)、売上は減少し、利益は増加しますが、
- この減少を定量化できますか?はい、できます。それはアイテムの価格弾力性として知られています。簡単に言えば、価格の1%の変化に対する売上のパーセント変化を意味します。
- 実際の世界では、売上はしばしばプロモーションイベント、休日、割引などの影響を受けますが、価格を最適化するためにはこれらの外部要因の影響を除外し、ベースラインの売上を計算する必要があります。
- 価格の変化に対する売上の変化を定量化したら、ダイヤルをどこで止めるべきかを知る必要があります。これには、ほとんどの場合利益を最大化するという目的が必要です。利益 = 売上 * 利益率なので、利益が最大になる位置で止める必要があります。数学的には、値が範囲内で移動できる非線形最適化の概念です。
- ビジネスルールは重要です。最終的な推奨価格がこれらのルールに準拠していることを確認する必要があります。
これが、与えられた店舗の各商品の正しい価格を導くために私たちが取る主要な手順です。これらの手順をもう少し詳しく見てみましょう。
1. ベースライン販売/ベースユニット
この手順は、後続の手順のためのプレステップです。述べたように、私たちは価格の変化による売上への影響をモデル化したいと考えています。理想的なシナリオでは、売上は価格の影響のみを受けることが望ましいですが、現実世界では常にそうではありません。
したがって、理想的なシナリオの売上をシミュレートしたいのですが、以下の方程式を用いた時系列モデルを使用して行います。
売上 ~ 関数[ベースライン販売 + (プロモーション効果) + (休日効果) + (その他の効果)]
なお、売上に影響を与える外部要因の実データを持っていない場合もあります。そのような場合には、ダミー変数を使用してそのような要因を考慮することができます。たとえば、ある月に売上が急増するが価格は変わらない場合、その月には1を持つ簡単なダミー変数を導入し、他の月には0を持たせることができます。
2. 価格弾力性
価格弾力性とは、特定の店舗のアイテムの価格の変化に対する売上の%変化を指します。
例として、ミルクとABC緑茶の2つの製品を考えてみましょう。どちらが高い価格弾力性を持つと思いますか?
ミルクは、高い競争力を持つ日常的な必需品であり、広範な需要があるため、高い価格弾力性を示します。価格のわずかな変化でも売上に大きな影響を与えることがあります。一方、ABC緑茶は限られた数の店舗でしか入手できないため、価格弾力性は低いです。ABC緑茶の価格のわずかな変化は売上に大きな影響を与えることはないでしょう。
これをどのようにモデル化するのでしょうか?
ベースライン販売 ~ 関数[価格 + トレンド]
価格変数の係数を価格弾力性として使用します。トレンド変数は、価格の変化ではなく、長期的なトレンドによる売上増加を考慮するために使用されます。価格弾力性の計算の詳細については、以下の価格弾力性セクションでさらに詳しく説明します。
3. 境界内の非線形最適化
この手順では、ダイヤルをどこで停止すべきかの答えを得ます。
まず、目的関数を定義します — 利益の最大化
次に、価格メーターの開始点と終了点を定義します。これにより、価格のLBとUBが定義されます。
既にベースライン販売と価格弾力性を計算しており、これらは価格への売上の感度を定量化しています。これらのすべての入力を非線形最適化関数に入力し、最適化された価格を得ます。
非常に簡単に言えば、アルゴリズムは境界内の異なる価格ポイントを試し、私たちの場合は利益という目的関数の値を確認します。目的関数の最大値を得る価格ポイントに戻ってきます。 (線形最適化では、勾配降下法がどのように機能するかを視覚化してください)。最適化された価格の計算の詳細については、以下の最適化セクションでさらに詳しく説明します。
4. ビジネスルール
では、最適化された価格を直接店舗に実装できるでしょうか?
いいえ、では現在は何が残っているのでしょうか?ビジネスルールの遵守は、どんなビジネスにとっても最も重要な要件の一つです。
ただし、価格設定にはどのようなルールがあるのでしょうか。
- 最後の数字のルール — 製品を$1000ではなく$999または$995で価格設定することは一般的な慣行です。そのような理由がいくつかあるため、最終的な推奨価格がこれに適合するかどうかを確認する必要があります。
- 製品のギャップルール — 1パックのMaggiの価格が4パックのMaggiよりも高くなることはありますか?いいえ、ありません。パックのサイズが増えると、単位あたりのコストは下がるか、少なくとも同じになることがよくあります。
これらは、ビジネスが適用したいいくつかのビジネスルールの例です。最終的な推奨価格を得るために、最適化された価格に対していくつかの後処理の手順を行います。
全体のプロセスについて理解しているので、詳細とコーディングについて掘り下げる時間です。
2. 弾力性モデリング
このセクションでは、複数の店舗で数千のアイテムの最適な価格を導出するためにこの概念をどのように使用できるかを理解します。例えば、過去3年間カリフォルニアの店舗で販売されているスナックアイテムYochipsの価格弾力性を決定する必要があるとしましょう。まずは価格弾力性の定義を見てみましょう:
価格弾力性とは、価格の1%の変化に対する売上のパーセンテージ変化と定義されます。
さて、Yochipsのようなアイテムの価格弾力性を計算するためにどのアルゴリズムを使用できるか気になるかもしれません。
経済書にある一定の価格弾力性モデルの詳細を見て、それをデータサイエンスのアルゴリズムに関連付けることができるか見てみましょう。
需要関数の乗法形式は次のようになります:
Yi = α*Xi (ここでyは売上/需要を表し、xは価格を表します)
両辺に対数を取ると
log(Yᵢ) = log(α*Xᵢ^β)
log(Yᵢ) = log(α) + β*log(Xᵢ) ……….Eq(1)
log(α)はβ₀として切片と考えることができます
log(Yᵢ) = β₀ + β₁*log(Xᵢ) ………….Eq(2)
さて、両辺を微分すると
δY/Y = β₁*δX/X
左側の項はYの%変化を表し、売上の%変化を表します。右側の項は価格の%変化を表します。ここで
%価格の変化 = 1%の場合、δX/X = 1
δY/Y = β₁
これは売上の%変化がβ₁であり、それが私たちの弾力性です。
さて、もし気づいているかもしれませんが、式2は対数売上を対数価格に回帰させる回帰式であり、対数価格の係数が価格弾力性です。
やった!弾力性の計算が回帰モデルのトレーニングと同じくらい簡単であることがわかりました。
ただし、もう1つ注意点があります。需要関数の式にはいくつかの仮定があり、そのうちの1つは売上は価格の影響のみを受けるというものですが、現実の世界では通常そうではありません。プロモーション、休日、イベントなど、売上に影響を与える要因は一般的に複数あります。では解決策は何でしょうか、これらの追加イベントの影響を除外できる売上の成分を計算する必要があります。
はっきりさせるべき一つのことは、基本売上は単位売上ではなくドル売上を指すということです。したがって、式2では実際の単位売上ではなく基本単位に対して価格を回帰させる必要があります。では、実際の単位売上から基本単位をどのように導出できるのでしょうか?
以下は、時系列の売上単位と販売価格の週別プロットが表示されています:
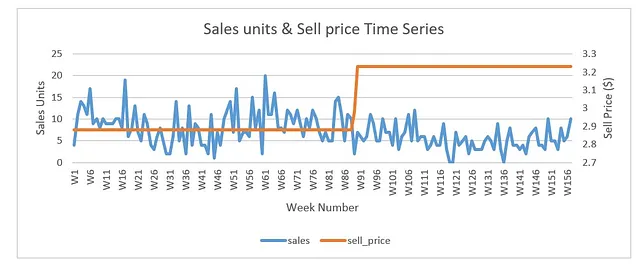
上記のプロットでパターンを見ることができますか?売上単位の系列には多くの変動があるため、判断するのは難しいです。これらの変動は休日、プロモーション、イベント、FIFAワールドカップなど、複数の要因によるものです。価格変動の影響を分離するために、これらの追加要素の影響を除外した売上を計算する必要があります。
Prophetモデルを使用することで、時系列を分解し、トレンド成分(基本売上)を抽出することができます。この技術を適用することで、価格変動の長期的な影響を他の短期的な要素から分離することができます。以下に、何について話しているのか見てみましょう:
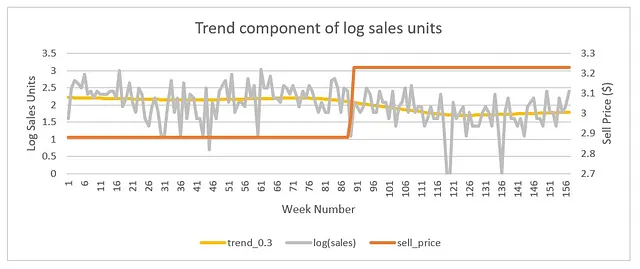
上記のプロットでは、元の対数売上単位(灰色)を対数基本単位(黄色の線のプロット)に分解しました。
以下のコードは、時系列を分解し、基本売上となるトレンド成分を取得する方法を示しています:
# 入力を定義する
timestamp_var = "week_ending_sunday"
baseline_dep_var = "ln_sales"
changepoint_prior_scale_value = 0.3
list_ind_vars_baseline = ['event_type_1_Cultural', 'event_type_1_National', 'event_type_1_Religious', 'event_type_1_Sporting']
# データの準備
closetdf_item_store = df_item_store.rename(columns={timestamp_var: 'ds', baseline_dep_var: 'y'})
df_item_store['ds'] = pd.to_datetime(df_item_store['ds'])
# モデルの初期化と学習
model = Prophet(changepoint_prior_scale=changepoint_prior_scale_value) #デフォルトのchangepoint_prior_scale = 0.05
# モデルに回帰変数を追加
for regressor in list_ind_vars_baseline:
model.add_regressor(regressor)
model.fit(df_item_store)
# 現在の時系列データのみを分解するため、モデリングに使用した予測データを使用する
# 予測を行い、レベルの成分を抽出する
forecast = model.predict(df_item_store)
level_component = forecast['trend']以下は定義する必要のある入力です:
- changepoint_prior_scale_value — これはトレンドの滑らかさを制御します。詳細については、Prophetモデルのドキュメントを参照してください。
- list_ind_vars_baseline — これには、祭り、スポーツイベント、文化イベントなど、売上に影響を与えた他のイベントが含まれます。
changepoint_prior_scale_valueがトレンドに与える影響を以下の画像で確認できます。値が小さい場合はほぼ直線になり、値が大きい場合はトレンドが滑らかではありません。
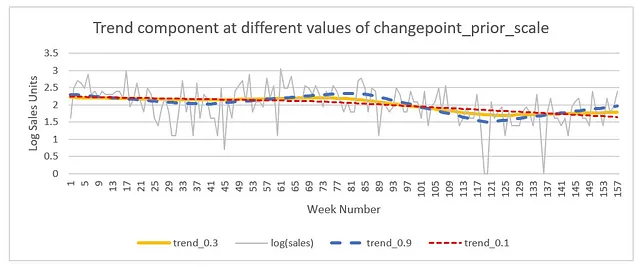
このコードはシンプルです。最初に、「ln_sales」という変数を「y」として、「week」という変数を「ds」として名前を変更して、Prophetモデルの前提条件を満たします。次に、Prophetモデルを初期化し、「changepoint_prior_scale」パラメーターを指定します。その後、モデルに追加のイベントおよび祝日の変数を組み込みます。最後に、モデルをトレーニングしたデータセットを使用して予測を生成し、トレンド成分を抽出します。
素晴らしいです。ベースユニットのシリーズができたので、ベースユニット(すでに対数スケールになっているため、log_base_unitsシリーズを分解しました)とlog(price)の間に線形回帰モデルを適合させることができます。以下は式です:
log(ベースユニット) = 切片 + 弾力性*log(価格)
上記の式を使用して、弾力性の値を計算できます。実際には、すべてのシリーズがモデル化に適しているわけではないため、さまざまなアイテムの予期しない弾力性の値が予想されることがあります。では、解決策は何でしょうか?弾力性の値に制約を設けた回帰をなんとか実行できれば良いのですが、どのように実装すれば良いのでしょうか?最適化関数を使用します。
最適化のためには、以下の基本的な要件があります:
- 目的関数 — 最小化/最大化しようとする方程式です。私たちの場合、線形回帰の損失関数MSE(予測-実際 => [切片 + 弾力性*ln_price – 実際]²)になります。
- パラメーターの初期値。私たちの場合、切片と弾力性です。最初は任意のランダムな値を使用できます。
- パラメーターの境界。切片と弾力性の両方に対する最小値と最大値です。
- 最適化アルゴリズム。これはライブラリに依存しますが、デフォルト値を使用すれば正しい結果が得られます。
では、以下にコードを示します:
# 最適化アルゴリズムにフィードするための行列の準備
x = df_item_store_model
x["intercept"] = 1
x = x[["intercept", "ln_sell_price", "ln_base_sales"]].values.T
# x_t = x.T
actuals = x[2]
from scipy.optimize import minimize
# 最小化する目的関数を定義
def objective(x0):
return sum(((x[0]*x0[0] + x[1]*x0[1]) - actuals)**2) # (切片*1 + 弾力性*(ln_sell_price) - ln_base_sales)^2
# 初期推測値を定義
x0 = [1, -1]
# 変数の境界を定義
bounds = ((None, None), (-3, -0.5))
# SLSQP最適化アルゴリズムを使用して目的関数を最小化
result = minimize(objective, x0, bounds=bounds, method='L-BFGS-B')
# 最適化結果を出力
print(result)
# アイテムの価格弾力性をデータフレームに保存
price_elasticity = result.x[1]
df_item_store_model["price_elasticity"] = result.x[1]初期パラメータの値を、切片の値を1、弾力性の値を-1と定義していることに注意してください。切片には上下限が定義されていませんが、弾力性には(-3、-0.5)の上下限が定義されています。これが、回帰を最適化関数を通じて実行している主な理由です。最適化を実行した後、価格弾力性の最適化されたパラメータ値を保存します。やった!価格弾力性を計算しました!
したがって、私たちのカリフォルニア店のYochipsの価格弾力性は-1.28です。
他のシリーズの価格弾力性も見てみましょう:
低価格弾力性:価格上昇による売上のほとんど変化がありません。価格弾力性が-0.5のアイテムのプロットが以下に示されています。
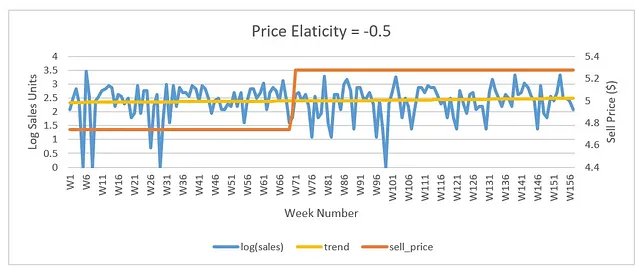
VoAGI価格弾力性:価格上昇による売上の中程度の減少があります。価格弾力性が-1.28のアイテムのプロットが以下に示されています。
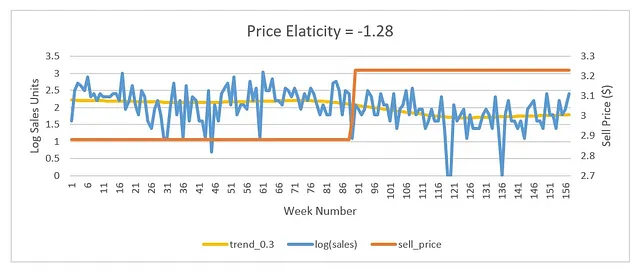
高価格弾力性:価格上昇による売上の大幅な減少があります。価格弾力性が-2.5のアイテムのプロットが以下に示されています。

同じアプローチを使用して、すべてのアイテムの価格弾力性を計算できます。次の記事では、これらの弾力性の値を活用して各アイテムの最適化された価格を決定する方法について調査します。
3. 最適化
前のセクションでは、カリフォルニア店のYochipsの価格弾力性をすでに求めました。しかし、それは店長の役に立たないので、Yochipsの価格をどのように変更すれば収益を最大化できるかを知りたいのです。この記事では、価格の最適化手法について理解します。
しかし、その前に、店長にいくつかの質問をしなければなりません。
Q: 価格の最適化時に考慮すべき最小価格変更と最大価格変更の制限はありますか?
店長との話し合いに基づいて、価格の減少は20%を超えてはならず、価格の上昇も20%に制限されることが分かりました。
Yochipsの現在の価格は3.23ドルですが、最適化された価格は2.58ドルから3.876ドルの間であることが分かりました。しかし、最適な価格をどのように導出すればよいのでしょうか?
しかし、収益を最大化するために価格を最適化する必要があります。ただし、価格の変更に伴い、総売上数量も変化します。上記の式を再度書き直し、最適化価格での総売上数量を最適化数量と呼ぶことができます:
最適化収益 = 総売上数量 * (最適化価格)
収益を最大化するために価格を最適化する必要があります。ただし、価格の変更によっても総売上数量は変わります。上記の式を再度書き直し、最適化価格での総売上数量を最適化数量と呼ぶことができます:
最適化収益 = 最適化数量 * (最適化価格)……………(式1)
すでに知っているように、-
弾力性 = 売上数量の%変化 / 価格の%変化
したがって、-
最適化数量 = ベース数量 + 最適化価格での数量の変化
ここで、ベース数量は現在の価格での総売上数量を指します(2.58ドル)
最適化数量 = (ベース数量 + (ベース数量 * 価格弾力性 * (最適化価格と通常価格の変化率) ………. (式2)
式2を式1に代入しましょう
最適化収益 = (ベース数量 + (ベース数量 * 価格弾力性 * (最適化価格と通常価格の変化率) * (最適化価格) …….. (式3)
最適化収益 = (ベース数量 + (ベース数量 * 価格弾力性 * [(最適化価格 – 現在の価格) / 現在の価格]] * (最適化価格)…………..式4)
以下は最適化方程式(eq4)の主要なパラメータです:
基本単位 = 現在の価格での平均売上単位数。
価格弾力性 = 項目の価格弾力性の計算値
現在の価格 = 最新の販売価格
素晴らしい!最適化方程式では、最適化された価格以外のすべての変数のデータがあります。したがって、収益を最大化する最適化された価格を計算するためにどのアルゴリズムを使用できますか? 単純に最適化アルゴリズムを使用できます。
最適化に必要な重要なコンポーネントは次のとおりです:
- 最小化/最大化する目的関数:既にeq(4)で定義された最適化された収益を最大化する目的関数を定義しています。
- 範囲:店舗マネージャーによって定義されたように、最適化された価格が現在の価格から20%以上変化しないようにする必要があります。したがって、下限 = 現在の価格(1–0.2)および上限 = 現在の価格(1+0.2)です。
- 最適化アルゴリズム:最適化を実装するために、PythonのScipy.optimizeライブラリを使用します。
コードを見てみましょう:
# 最新の6週間の基本販売の平均を取る
df_item_store_optimization["rank"] = df_item_store_optimization["ds"].rank(ascending=False)
# 最新の6週間のデータを抽出し、idごとにbase_salesの平均を計算する
database_sales_df = df_item_store_optimization.loc[df_item_store_optimization["rank"] <= 6].groupby("id")["base_sales"].mean().reset_index()
df_item_store_optimization_input.rename(columns = {"base_sales":"base_units"}, inplace=True)
# 売価の最小値と最大値の範囲を導出する
df_item_store_optimization_input["LB_price"] = df_item_store_optimization_input["sell_price"] - (0.2*df_item_store_optimization_input["sell_price"])
df_item_store_optimization_input["UB_price"] = df_item_store_optimization_input["sell_price"] + (0.2*df_item_store_optimization_input["sell_price"])上記のコードは、最適化のためのデータ準備を支援しています。まず、基本単位を計算しています。これは、最新の6週間のbase_sales(分解された時系列のトレンド成分)の平均です。上記のセクションでbase_salesを計算する方法については既に説明しました。
次に、LB_priceとUB_priceを定義し、それぞれ現在の販売価格から20%減算および増加させます。
次に、最適化を実行するためのコードを定義しましょう。
from scipy.optimize import minimize
# 最小化する目的関数を定義
def objective(opti_price):
df_item_store_optimization_input["opti_price"] = opti_price
df_item_store_optimization_input["optimized_units"] = df_item_store_optimization_input["base_units"] + (df_item_store_optimization_input["base_units"]*\ ((df_item_store_optimization_input["opti_price"]/df_item_store_optimization_input["sell_price"]) - 1)*\ (df_item_store_optimization_input["price_elasticity"]))
df_item_store_optimization_input["optimized_revenue"] = df_item_store_optimization_input["optimized_units"]*df_item_store_optimization_input["opti_price"]
return -sum(df_item_store_optimization_input["optimized_revenue"])
# 初期推測値を定義
opti_price = df_item_store_optimization_input["sell_price"][0]
# 変数の範囲を定義
bounds = ((df_item_store_optimization_input["LB_price"][0], df_item_store_optimization_input["UB_price"][0]),)
# 最適化アルゴリズムを使用して目的関数を最小化
result = minimize(objective, opti_price, bounds=bounds)
# 最適化結果を表示
print(result)上記のコードは最適化された価格を得ます。目的関数のなかでなぜ最適化された収益の負の値を定義しているか推測できますか?-(-1)は1です。私たちは目的関数を最小化しているため、最適化された収益の負の符号を使用すると、最適化された収益を最大化することになります。
さらに、opti_price変数を任意のランダム値で初期化することができますが、収束を早めるために現在の売価で初期化しています。boundsでは、上記のコードで作成したLBおよびUBを定義しています。
やったー!Yochipsの最適化された価格を見つけました。これをカリフォルニア店のマネージャーに提案する準備ができました。

私たちの推奨は、Yochipsの価格を10.2%引き下げて$2.9にすることです。これにより、最大の収益が得られます。
これは価格最適化アプローチの最後のステップであり、全体的なアプローチは非常に強力であり、すべての店舗の各アイテムに最適化された価格を返すのに役立つことができます。
上記のアプローチの制約の1つは、価格変動の履歴が十分でないアイテムの場合です。その場合、他の技術を使用しますが、そのアイテムの割合が少ない場合は、カテゴリーレベルの平均価格弾力性を使用することができます。
この記事がお楽しみいただければ幸いです!
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
