マルコフとビネメ・シェビシェフの不等式

Markov and Chebyshev's inequalities

2つの境界の意味と、それらの発見に繋がった驚くべき連続した出来事についての詳細な調査

宇宙が何かを単純にできないと言うことは、あまりありません。どれだけ賢くても、どれだけ豪華な財源があっても、どの宇宙の隅にいようとも関係ありません。宇宙が「不可能」と言った時、その道は二つではありません。科学において、そのような不可能性は、いくつかの数量の値に制約を課すことで表現されることがよくあります。有名な例としては、アルベルト・アインシュタインが1905年に発見したことがあります。それは、宇宙の真空中に光子を放すと、それを追い越すことができないということです。これまでに、数百ものそのような制約や境界が発見され、証明されています。それらは、現実の性質を囲むフェンスを形成しています。

マルコフとビネイメ・チェビシェフの不等式は、ランダムな出来事がどれだけ頻繁に発生するかについて、自然が制限を設けるという私たちの認識を深く形作っています。

マルコフの不等式の発見と証明は、優れたロシアの数学者で情熱的な信念を持つアンドレイ・アンドレーエヴィッチ・マルコフ（1856年-1922年）によって行われました。

ビネイメ・チェビシェフの不等式の功績は、二人に帰属しています。確率論の巨人であり、マルコフの教師でもあるパフヌティ・レヴォヴィッチ・チェビシェフ（1821年-1894年）と、チェビシェフのフランス人の同僚で友人であるイレネ・ジュール・ビネイメ（1796年-1878年）です。

• 「監督のギレルモ・デル・トロとティム・バートンはAIについて異なる見解を持っています」
• エンテラソリューションズの創設者兼CEO、スティーブン・デアンジェリス- インタビューシリーズ
• 「ランバード効果と聴覚障害への役立ち方」

これらの不等式の発見には、特にビネイメ・チェビシェフの不等式には、驚くべき歴史が関連しており、単に数学を説明するだけでは不十分です。私はこれらの背景を明らかにしようとします。そしてそれをすることで、不等式の基礎となる数学を説明するための文脈を設定します。

まずはマルコフの不等式から始め、マルコフの不等式にいくつかの簡単な変数の置換を行うことでビネイメ・チェビシェフの不等式が生じることを示します。さらに、もう一組の変数の置換を行うことで、ビネイメ・チェビシェフの不等式から「大数の弱法則」（WLLN）の証明を得るためのボーナスがあります。

マルコフの不等式

マルコフと言えば、「マルコフ連鎖」、「マルコフ過程」、「マルコフモデル」が思い浮かびます。厳密には、マルコフ連鎖はA. A. マルコフが創造したものです。しかし、マルコフの数学への貢献は、マルコフ連鎖と確率論をはるかに超えています。マルコフは、数論、連分数、微積分、統計のさまざまなアイデアについて、広範な研究を行いました。ちなみに、マルコフは、博士の指導教官であるP. L. チェビシェフが主に西欧、特にフランスの出版物で多くを発表していたのとは対照的に、主にロシア語のジャーナルで発表していました。

1900年、マルコフがキャリアの絶頂にいた可能性が高い時期に、彼は「確率の計算」という題名の画期的な本を出版しました。

この本は4版とドイツ語版がありました。マルコフは1913年に意図的に自身の本の第3版を出版しました。それは大数の弱法則（WLLN）の200周年を祝うためでした。第3版にはWLLNに関する大量の素材があります。しかし、補題に隠されているのは、マルコフの証明が統計科学の分野において非常に中心的な法則であり、WLLN自体の証明の出発点としてよく使用されることがわかりました。

マルコフが示したのは次のことです：

任意の非負の確率変数Xを想像してください。 Xは、朝の起床時間などのありふれたものから、銀河の星の数のような巨大なものまでを表すことができます。 Xは離散的または連続的な値を持つことができます。 Xは任意の種類の確率分布を持つことができます。つまり、Xは任意の非負のランダムな現象を表すことができます。さて、Xの範囲内で値を選択してください。この値を「a」とします。「自然は、選んだ値 ‘a’ 以上の値 X を観測する確率に上限を課す」とマルコフは示しました。そして、この上限は ‘a’ が大きくなるにつれて縮小します。選んだ値 ‘a’ が大きければ大きいほど、値 ‘a’ を超える値 ‘b’ を観測する確率は低くなります。言い換えれば、自然は外れ値を嫌います。

説明するために、次のプロットをご覧ください。これは、アメリカ合衆国の上位20州の郡の一人当たりの個人所得の頻度分布を示しています。

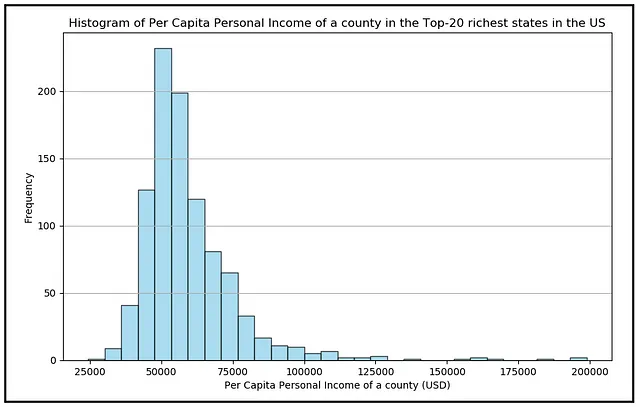
ここで、ランダム変数Xはランダムに選ばれた郡の一人当たりの所得です。

さて、一人当たりの所得に対するある閾値 ‘a’ で作業しましょう。次のイメージパネルでは、赤い領域はX ≥ a を表し、a = $50000、$70000、$80000です。

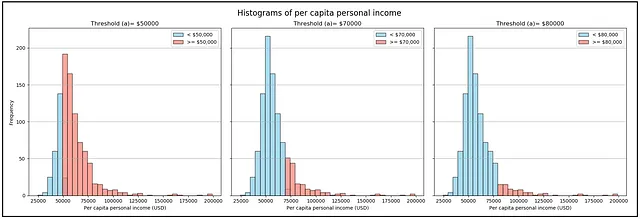
確率 P(X ≥ a) は、赤い領域の面積をヒストグラムの総面積で割ったものです。この確率 P(X ≥ a) は、’a’ が増加するにつれて減少することが容易にわかります。これは ‘a’ の逆数に関係しています。マルコフの定理は、この確率に逆数に関連する上限を課します。そして、この関係はXの分布に関係なく成り立ちます。

しかし、それだけではありません。

同じ不等式の一環として、マルコフはまた、Xの平均値がX ≥ a を観測する確率に直接的な影響を与えることも示しました。つまり、Xの平均値が大きいほど、この確率の上限も高くなり、逆もまた成り立ちます。言い換えれば、Xの確率の集積がXの範囲の上側にシフトすると、P(X ≥ a) の上限も増加します。逆に、Xの確率の集積が下側にシフトして「下重い」状態になると、Xの大きな値を観測する確率は減少します。

これらの中には、日常の常識のように思えるものもありますが、マルコフの素晴らしさは、’a’、P(X>=a)、およびXの平均（期待値とも呼ばれる）であるE(X)の間に数学的に正確な関係を確立することにあります。彼は次のように示しました：

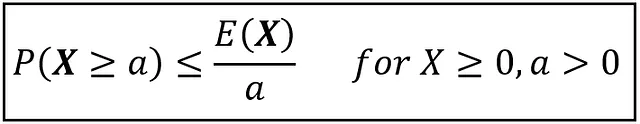
マルコフの不等式の証明

マルコフの不等式を証明する方法はいくつかありますが、私はXが離散的であるか連続的であるかに関係なく機能する単純な技術を説明します。ただし、Xは非負である必要があります。

前述のとおり、興味があるしきい値 ‘a’ で作業します。

次に、0 ≤ X < a の場合はI = 0、X ≥ a の場合はI = 1となるランダム変数Iを定義します。統計用語では、Iはインジケータ変数と呼ばれます。

X ≥ a の場合を考えて、両辺にIを掛けます：

XI ≥ aI

X ≥ a の場合、I = 1 です。したがって、XI = X です。

したがって、

X ≥ aI は、I = 1 の場合に成り立ちます（この結果を覚えておきましょう）。

Xは非負であるため、0 ≤ X であり、ある正の ‘a’ に対して、X は ‘a’ より小さいか、 ‘a’ 以上である場合があります。すでにXが ‘a’ 以上の場合を考慮しました。したがって、0 ≤ X < a の場合を考慮しましょう。

I の定義によれば、X < a の場合、I = 0 です。

したがって、aI = a0 = 0 です。

Xは非負であることが仮定されているため、すなわち X > 0 かつ aI = 0 のため、X ≥ aI です。

したがって、I = 1 の場合でも I = 0 の場合でも、aI <= X です。

この不等式の両辺に期待値演算子 E(.) を適用しましょう：

E(aI) <= E(X)

定数 ‘a’ を取り出します：

aE(I) <= E(X)

E(I) について考えましょう。ランダム変数 I は、X < a および X≥ a に対応する 0 と 1 の2つの値しか取ることができません。各イベントに関連する確率は、それぞれ P(X < a) および P(X >= a) です。したがって、

E(I) = 0P(X < a) + 1P(X >= a) = P(X >= a)

この結果を aE(I) <= E(X) に代入すると、次のようになります：

aP(X >= a) <= E(X)

そして：

P(X >= a) <= E(X)/a、これはマルコフが証明した不等式です。

ビエナイム・チェビシェフの不等式

ビエナイム・チェビシェフの不等式は、確率変数の平均から値「a」だけ離れた値を観測する確率が、マルコフの不等式と同様に制約されていることを述べています。言い換えると、自然は確率 P(|X — E(X)| >= a) に上限を課しています。この上限は a² に反比例し、X の平均からのばらつき（分散）に直接比例します。数式的には、ビエナイム・チェビシェフの不等式は以下のように表されます：

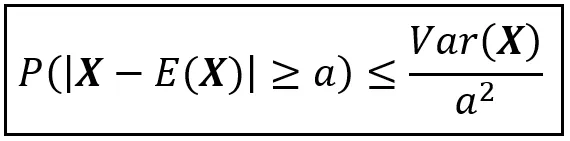
マルコフの不等式と同様に、ビエナイム・チェビシェフの不等式の素晴らしさは、X の確率分布について何の仮定もしないことにあります。 X は正規分布、指数分布、またはガンマ分布としても構いません。 X は牛の影の形状で分布していても構いません。ビエナイム・チェビシェフの確率上限は堅固に成り立ちます。

ビエナイム・チェビシェフの不等式の歴史的な逸話

ビエナイム・チェビシェフの不等式の発見には興味深い歴史があります。まず、この不等式においてジュール・ビエナイムの名前がチェビシェフの名前よりも前に来る理由があります。

1853年、フランスの数学者イレネー＝ジュール・ビエナイムは、フランス科学アカデミーの論文集で最も重要な論文の一つを発表しました。ビエナイムの論文は表面的にはラプラスの最小二乗法の扱いについてでしたが、その中で彼はビエナイム・チェビシェフの不等式を述べ、証明しました（当時はチェビシェフの名前はまだ関係していませんでした）。しかし、ビエナイムは謙虚な性格からくる注意散漫さのために、自身の発見の重要性を十分に認識せず、それはほぼ無視されたままでした。そして、もしパフヌティ・リヴォヴィチ・チェビシェフが足の筋肉が萎縮して生まれていなかったら、確率論における最も重要な成果の一つが埋もれたままになっていたかもしれません。

ビエナイムがフランス財務省の公務員として足場を固めていた1821年の初夏、ペテルブルクから南に100マイル離れた村で、25歳のビエナイムの元にパフヌティ・リヴォヴィチ・チェビシェフが生まれました。チェビシェフは9人兄弟の一人で、幼少期から機械工学と数学の両方に卓越した才能を示しました。チェビシェフの父は軍人で、1812年のナポレオンによるロシア侵攻の際にナポレオンを撃退しました。歴史の奇妙な皮肉の一つとして、わずか2年後、ナポレオンの撤退後の混乱した状況で、ジュール・ビエナイムはナポレオンを支援し、パリに進撃してきたロシア、オーストリア、プロイセン軍を撃退することになります。もちろん、ナポレオンはパリを守ることに完全に失敗し、エルバ島に追放されました。

このすべての歴史は、パフヌティ・ラヴォヴィッチの誕生よりもはるかに前に展開されました。しかし、彼の軍人の家系と家族の伝統を考えれば、先天的な筋萎縮した足がなければ、P. L. チェビシェフはおそらく兄弟のいく人かと一緒にツァールの軍隊に入隊し、確率の歴史はまったく異なる方向を取っていたかもしれません。しかし、チェビシェフの数学への入門や後にロシアの学界への入門は、彼のビネメの紹介に対する唯一の触媒ではありませんでした。そして、それによって彼はビネメ-チェビシェフの不等式への貢献を支持しました。

子供の頃、チェビシェフはフランス語で自宅学習をしました。キャリア初期に彼は、自国外で彼の仕事が読まれるようになるために、19世紀の数学研究の世界の首都であるパリで知られる必要があると気づいたようです。

チェビシェフは、フランスや他の西欧の首都に頻繁に旅行し、彼の80の論文のほぼ半分を西欧のジャーナルで発表しました。その多くは、フランスの数学者ジョゼフ・リウヴィルが編集するJournal des Mathématiques Pures et Appliquées（純粋応用数学ジャーナル）に掲載されました。1852年のヨーロッパツアー中に、チェビシェフはビネメと出会いました。この相互に利益のある友情は、チェビシェフに多くのヨーロッパの科学者や出版社へのアクセスを与え、またビネメ自身の数学への貢献をフランスとロシアの主要な雑誌で当然のように宣伝しました。

もちろん、重要な作品の1つは、ビネメが1853年に彼の名前を冠する不等式を発見したことです。これがこの不等式の研究に戻るということになります。

実際にビネメが1853年の論文で証明したのは次のことです。

平均と分散がそれぞれμとσ²である値の集団からサイズNの無作為抽出サンプルを作成するとします。サンプル平均X_barを作成します。ちなみに、サンプル平均X_barは、それ自体がμとσ²/Nである期待値と分散を持つランダム変数であることが示されます。頭をかいているなら、安心してください。すぐにサンプル平均の期待値と分散の導出方法を示します。一方、話題に戻ると、ビネメが示したのは次のことです。

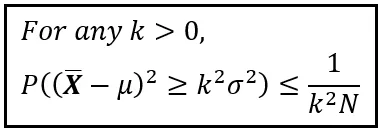
さて、おそらく気になるのは、チェビシェフがビネメの発見と密接に関わり、この不等式にチェビシェフの名前が付けられるようになるのはいつなのかということです。

実は、ビネメが不等式を発表してから14年後、チェビシェフはビネメの発見に完全に無知のまま、ジョセフ・リウヴィルのジャーナルの1867年号にこの不等式の異なるバージョンを発表しました。念頭に置いておいてください、これはGoogleやCiteSeer、電話の前の時代です。したがって、当時の科学者が「以前の研究」について完全に認識していなかったと言うことは、問題のスケールをほのめかすに過ぎません。

1874年に発表された論文で、シェビシェフはこの不等式の発見を完全にビネメに帰属しています：

「私のノート『平均値について』に記載されているベルヌーイの法則の単純かつ厳密な証明は、ただの一つの結果に過ぎず、容易に導かれる結果です。それはM.ビネメの方法から直接導かれるものであり、彼自身が確率の定理を証明したものであり、そこからベルヌーイの法則が直ちに導かれます」

その後の数年間、シェビシェフの不等式（正確にはビネメ-シェビシェフの不等式）は、期待値E(X)と有限の分散Var(X)を持つ任意の確率変数Xに単純に適用されるバージョンとして知られるようになりました。

ビネメ-シェビシェフの不等式は、任意の正の「a」に対して、確率P(|X – E(X)| ≥ a)が以下のように制約されることを述べています：

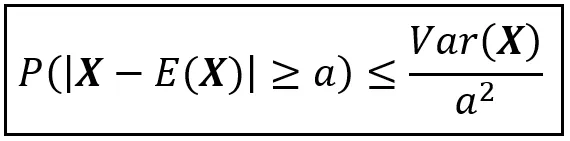
ビネメ-シェビシェフの不等式の証明

マルコフの不等式（彼の名前を冠した）は、1913年の彼の著書「確率論の微积分」で証明され、ビネメ-シェビシェフの不等式の証明によく使われます。マルコフの不等式を出発点として、結果を証明することは簡単です。以下のように証明します：

平均E(X)を持つ確率変数Xを考えましょう。ここで、別の確率変数Z = (X – E(X))²を定義しましょう。二乗項により、Zは非負であることが保証され、Zにマルコフの不等式を適用することができます。ここで、Zと呼ぶしきい値の値をa²とします。観測されたZの値がa²以上になる確率はP(Z ≥ a²)です。マルコフの不等式をZとa²に適用すると、次のようになります：

上記の式から始めると、次のようにビネメ-シェビシェフの不等式を導くことができます：

式（3）はビネメ-シェビシェフの不等式（または単にシェビシェフの不等式）です。

任意のしきい値「a」ではなく、標準偏差σに基づいて「a」を表すことが便利です：

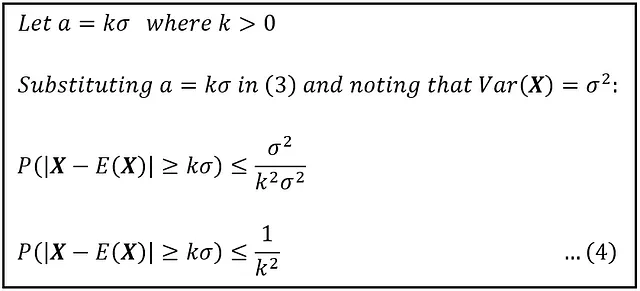
上記の証明は、1853年の彼の著書で示されたBienayméのオリジナルの結果の証明への直接の道も開いています。具体的には以下の通りです：

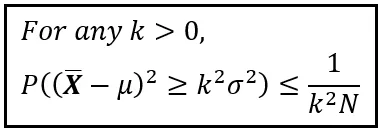
式（2）から始めて、Xを標本平均X_barに、a²をk²σ²に置き換えることで、Bienayméの1853年頃の結果に至ります：

式（4）と（4a）は興味深い結果を示しています。それらは、平均から少なくともk個の標準偏差離れた観測値に出くわす確率が上限であり、この上限はk²に反比例すると言っています。

言い換えると、平均値から数個の標準偏差離れた値に出くわすことは非常に少ないということです。

このように表現すると、Bienaymé–Chebyshevの不等式は、「あまりにも良いと思えるものは、おそらくそうではない」ということわざや、科学者の永遠のお気に入りである「非常な主張には非常な証拠が必要」といったことわざに数学的な根拠を与えています。

この不等式の動作を説明するために、以下のデータセットを考えてみましょう。これはシカゴ地域の1月1日の平均日温のデータセットで、1924年から2023年までの100の観測値が含まれています：

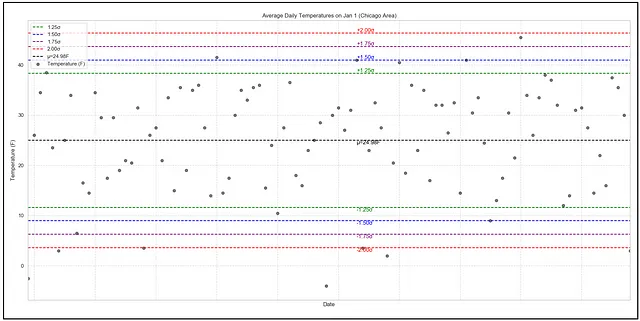
プラットのプロットの中央にある黒い点線の水平線は、24.98°Fの標本平均を示しています。色付きの水平線は、データサンプルの標準偏差の1.25倍、1.5倍、1.75倍、および2倍の温度値を示しています。これらの標準偏差の範囲内に、ほとんどの温度値が存在することがわかります。

Bienaymé–Chebyshevの不等式を適用することで、ランダムに選択された年の1月1日の観測された平均気温Xにおける確率P(|X – E(X)| ≥ kσ)の上限を求めることができます。ここで、E(X) = 24.98°F、σ = 10.67682°F、k = 1、1.25、1.5、1.75、および2.0です。以下の表は、これらの確率の上限を1/k²の列に示しています：

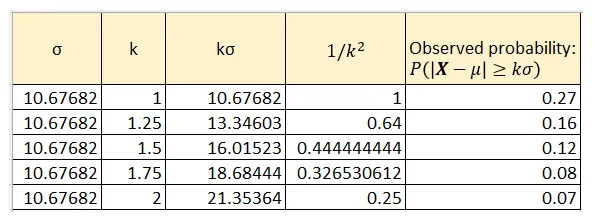
表の最後の列は、データサンプルにおけるそのような偏差の実際の確率を示しています。データサンプルで観測された実際の値は、Bienaymé–Chebyshevの不等式によって生成された確率の範囲内に快適に収まっています。

おそらく気づいたかもしれませんが、Bienaymé–Chebyshevの不等式によって生成される確率の範囲は非常に広いです。たとえば、k=1の場合（これは平均から1標準偏差以内にあるイベントに対応します）、不等式は確率の上限を1/1² = 1.0、つまり100%と計算します。これにより、この特定の範囲は実際にはほとんど役に立たなくなります。

ただし、k>1のすべての値に対して、この不等式は非常に有用です。その有用性は、ランダム変数の分布に特定の形状を仮定しないことにもあります。実際には、さらに適用範囲が広がります。マルコフの不等式では、ランダム現象が厳密に非負の観測値を生成する必要がありますが、Bienaymé–Chebyshevの不等式はXについてそのような仮定をしません。

Bienaymé–Chebyshevの不等式は、Weak Law of Large Numbersの一番簡単な証明も提供してくれます。実際、1913年にマルコフはこの不等式を使用して確率論の本でWLLNの証明を示しました。そして、多くの教科書で現在も使用されているのは本質的に同じ証明です。

大数の法則（およびその証明）

理論上無限に大きい集団からランダムにサンプルを収集するとしましょう。サンプルサイズをNとします。このランダムサンプルには、サンプル平均X_barがあります。サンプルサイズNが無限大に近づくにつれて、サンプル平均の誤差の確率が任意の正の許容値ϵよりも大きくなる確率がゼロに収束するというのがWLLNです。許容値ϵをどれだけ小さく選んでも構いません。サンプルサイズNが無限大に近づくと、P(|X_bar – μ| >= ϵ)はゼロに近づきます。

WLLNは、数学の巨人であるヤコブ・ベルヌーイをはじめ、ド・モワブル、ラプラス、ラクロワ、ポワソン、そして私たちの友人であるBienayméとChebyshevなど、300年以上にわたる発見の豊かな歴史を持っています。そして、Bienaymé–Chebyshevの不等式のおかげで、WLLNの証明は丘を駆け下る水のような簡単さで進行します。

大数の法則の証明

統計学の多くのことと同様に、証明は理論上無限に大きな集団からNのサンプルを引くことから始めます。このサンプルをX1、X2、X3、…、XNとします。これは、N個の変数、つまりN個のスロットのセットとして考えると便利で、サンプルが引かれるたびに集団からランダムに選択された値でそれぞれが埋められると考えることができます。したがって、X1、X2、X3、…、XNそれ自体がランダム変数です。さらに、X1、X2、X3、…、XNはお互いに独立であり、同一の分布（i.i.d.）を持つランダム変数です。

任意のランダムに選ばれたサンプルに対して、サンプル平均X_barは次のように計算できます：

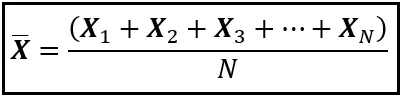
別のランダムサンプルを抽出すると、別のサンプル平均が得られ、3番目のサンプルを抽出すると、また別のサンプル平均が得られるため、サンプル平均X_barは、それ自体が平均と分散を持つランダム変数です。X_barの平均を計算しましょう。

また、サンプル平均の分散も計算しましょう。

さて、Bienaymé–Chebyshevの不等式をサンプル平均X_barに適用しましょう:

統計科学の領域において、WLLNとしても知られるこの驚くべき結果の証明が、これほどまでに驚くほど単純なものであるという事実は、自然の中の不条理の一つであり、人はただ驚嘆するばかりです。いずれにせよ、それがあります。

マルコフ不等式とBienaymé–Chebyshevの不等式、および大数の弱法則を合わせると、統計科学の大部分が確実に立脚している基盤が形成されます。例えば、統計モデル（またはニューラルネットモデル）をトレーニングする場合、トレーニングアルゴリズムはWLLNを遵守する必要があります。そうでない場合、係数の推定値は真の母集団の値に収束することが保証されません。そして、それはトレーニングテクニックを基本的に無用なものにします。WLLNはまた、もう1つの重要な結果である「中心極限定理」の証明にも使用されます。そして、それが私の次の記事の主題です。

参考文献と著作権

論文

Bienaymé, I.J. (1853) Considérations à l’appui de la découverte de Laplace sur la loi de probabilité dans la méthode des moindres carrés,” (“Considerations in support of Laplace’s discovery on the law of probability in the method of least squares.”) C.R. Acad. Sci., Paris 37 309–324. Also published in “Journal de Mathématiques Pures et Appliquées” (“Journal of Pure and Applied Mathematics”), Liouville, (2) 12 158–176. (1867)

Gely P. Basharin, Amy N. Langville, Valeriy A. Naumov, “The life and work of A.A. Markov”, Linear Algebra and its Applications, Volume 386, 2004, Pages 3–26, ISSN 0024–3795, https://doi.org/10.1016/j.laa.2003.12.041.

Bru, Bernard, François Jongmans, and Eugene Seneta. “I.J. Bienaymé: Family Information and Proof of the Criticality Theorem.” International Statistical Review / Revue Internationale de Statistique 60, no. 2 (1992): 177–83. https://doi.org/10.2307/1403648.

Eugene Seneta “A Tricentenary history of the Law of Large Numbers,” Bernoulli, Bernoulli 19(4), 1088–1121, (September 2013)

データセット

米国経済分析局「公共ドメインライセンスによる郡、都市圏、およびその他の地域の個人所得」。

全米気象局「公共ドメインライセンスによるシカゴ地域のオンライン天気データ」。

画像

この記事のすべての画像は、CC-BY-NC-SAの下でサチン・デートによる著作権があります。ただし、画像の下に異なる出典と著作権が記載されている場合を除きます。

読んでいただきありがとうございます！この記事が気に入った場合は、回帰分析と時系列分析に関するヒント、方法、およびプログラミングアドバイスを受け取るためにフォローしてください。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!