マーケティング予算の最適化方法

'Marketing budget optimization methods'

努力したマーケティングミックスモデルのトレーニングの成果を収穫する時が来ました！

マーケティングミックスモデルは、異なるマーケティングチャネルが売上に与える影響を理解するための強力なツールです。マーケターはマーケティングミックスモデルを構築することにより、各チャネルが全体の売上に与える貢献度を定量化し、その情報を活用して予算配分を最適化することができます。

これまでに、マーケティングミックスモデルの構築に関してはシリーズ全体を書いてきましたが、これらのモデルを使用してメディア支出を最適化する方法についての記事はまだ書いていませんでした。今日はあなたのラッキーデーです！なぜなら、この記事ではそれを具体的に紹介します。

マーケティングミックスモデリングが初めての方は、私の導入記事から始めることができます:

Pythonによるマーケティングミックスモデリングの導入

どの広告費が本当に売上を牽引しているのか？

towardsdatascience.com

• レオナルド・ダ・ヴィンチ：天才の心の内部
• ChatGPT CLI コマンドラインインターフェースをChatGPTに変換する
• Pythonを使用したMann-Kendall傾向検定

前提条件

何かを最適化する前に、まずモデルを構築する必要があります。できるだけ早く本記事のメインセクションに移るために、それを素早く行います。

データ

まず、いくつかのデータを読み込みましょう。私は古い記事と同じデータセットを使用します。

import pandas as pdfrom sklearn.model_selection import cross_val_score, TimeSeriesSplitdata = pd.read_csv(    'https://raw.githubusercontent.com/Garve/datasets/4576d323bf2b66c906d5130d686245ad205505cf/mmm.csv',    parse_dates=['Date'],    index_col='Date')X = data.drop(columns=['Sales'])y = data['Sales']

データセットは次のようになります:

このテーブルの背後にあるロジックは次のとおりです: ある製品を販売している会社で働いていると想像してください。週ごとの製品の売上をSales列で確認できます。これらの売上を増やすために、TV、Radio、Banner広告にお金を使います。そして、広告費や曜日、月、製品価格、天候などの制御変数を使って売上をモデル化したいのです。

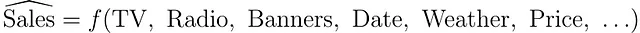
モデル

XGBoostやディープニューラルネットワークなどの複雑なモデルを構築すると、解釈や最適化が難しくなります。代わりに、理解しやすく最適化も可能な一般化加法モデルを構築するための確立された方法に頼ることにします。以下のように行います:

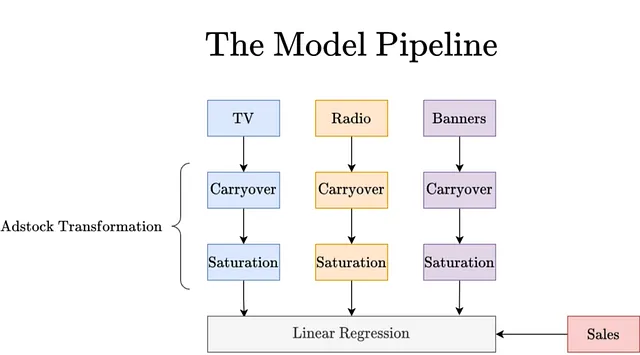
キャリーオーバーと飽和ブロックは直感的な特徴変換です:

• キャリーオーバーは、時刻tでのメディア支出がt + 1、t + 2、…の売上にまだ影響を与える可能性があることをモデル化します。または、時刻tで観測された売上も、時刻t – 1、t – 2、…の支出によって影響を受ける可能性があることもモデル化します。
• 飽和は、収益の減少率をモデル化します。例えば、あるチャネルへの支出を0 €から100,000 €に増やすと大きな影響がありますが、それを1,000,000,000 €から1,000,100,000 €に変更しても影響がなくなります。

注意：グラフィックでは、制御変数は省略されています。これは最適化には必要ないためです。私たちはメディアチャネルに投資する金額のように、それらを変更することはできません。唯一変更できる制御変数は価格ですが、ここでは一定と仮定し、実際にはメディア支出を最適化したいと考えています。

したがって、モデルは以下の形をしています

まだ定義されていないsaturationとcarryoverという関数を持っています。例えば、以下のように仮定しましょう

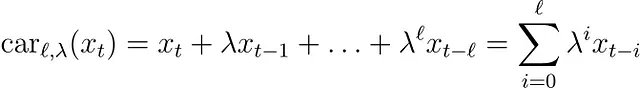
および

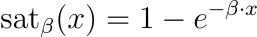
ここで、βは飽和係数、λは持ち越し強度、ℓは持ち越し長さです。

これらのパラメータは、ハイパーパラメータとして扱うか、ベイジアンメソッドを使用して通常の学習可能なパラメータとして扱うことで学習できます。マーケティングミックスモデリングに関する私の最後の記事では、これらのパラメータをどのように取得するか詳しく説明しましたので、ここではこれ以上詳しく触れません。

代わりに、これらの数値を持っていると仮定し、最適化されたメディア予算配分計画を作成したいと考えましょう。

メディア予算の最適化

以前のマーケティングミックスモデリングの試みにより、次のパラメータが残りました：

N = 200 # 観測回数# 以前のマーケティングミックスモデリングで得られたこれらのパラメータtv_coef = 10000       # αtv_lags = 4           # ℓtv_carryover = 0.5    # λtv_saturation = 0.002 # βradio_coef = 8000radio_lags = 2radio_carryover = 0.2radio_saturation = 0.0001banners_coef = 14000banners_lags = 0banners_carryover = 0.2banners_saturation = 0.001

これらのパラメータを使用して、numpyを使用してマーケティングミックスモデルを再構築します。

しかし、なぜですか？すでにscikit-learnやPyMCを使用してモデルを構築しました！これを再利用できませんか？

いい質問です！事前にトレーニングされたモデルを使用し、販売を最大化するメディア支出を見つけるような一般的な最適化アルゴリズムに渡すことができます。ただし、これはブラックボックス最適化と呼ばれ、グローバル最適値を見つける代わりにローカル最適値にはまりやすいという問題があります。

ブラックボックス最適化の別の問題は、アルゴリズムには通常、良い（しかし最適ではないかもしれない）解を見つけるために試行錯誤しなければならないさまざまなパラメータがあることです。そのため、この種の最適化は、科学よりもむしろ芸術と言われることがあります。

凸性のお助け

問題を凸最適化問題として定式化できれば、cvxpyなどのライブラリを使用して最適なメディア予算配分を見つけることが保証されます。私はすでに他の最適化問題を解決するためにこのライブラリを使用しました。

凸最適化メソッドを使用するためには、モデルが凸または凹でなければなりません。モデルの前にマイナス符号を付けることで、モデルを凸にすることができます。

例えば、私たちのモデルが y = x² であれば、それは最小化しやすい凹関数です。y = 100 – x² は最大化しやすい凹モデルです。

詳細には触れませんが、私たちのモデルは実際には凹関数です！私たちが作成したモデルであるキャリーオーバーサチュレーションモデルでは、飽和関数の2階導関数が負であれば、モデルは凹です。

ただし、Adbudgや他の典型的なS字型関数など、他の飽和関数を使用する場合は、凹でも凸でもないため、最適化がより困難になります。

さて、理論はここまでにしましょう。ただ今は、私たちのモデルが凹であることを覚えておいてください。これは素晴らしいことです。なぜなら、最大の売上をもたらす予算配分、つまりグローバルオプティマムが見つかるからです。

Numpyでのモデルの再実装

まず、キャリーオーバーエフェクトを処理するいくつかの行列を定義しましょう。

import numpy as np
tv_carryover_matrix = sum([np.diag(tv_carryover**i*np.ones(N-i), k=-i) for i in range(tv_lags)])
radio_carryover_matrix = sum([np.diag(radio_carryover**i*np.ones(N-i), k=-i) for i in range(radio_lags)])
banners_carryover_matrix = np.eye(N)

これは理解するのが難しいと思いますので、これらの行列の一つを見てみましょう。

これは強度が0.2で長さが1のキャリーオーバーを実装しています。これを支出ベクトルと掛け算すると、そのことがわかります。

これでキャリーオーバーが終わったので、次に飽和の処理に進みましょう。これは単純な exp の式であり、問題ありません。

次のように書けます：

sales = (    tv_coef * np.sum(1 - np.exp(-tv_saturation * tv_carryover_matrix @ data["TV"]))     + radio_coef * np.sum(1 - np.exp(-radio_saturation * radio_carryover_matrix @ data["Radio"]))     + banners_coef * np.sum(1 - np.exp(-banners_saturation * banners_carryover_matrix @ data["Banners"])))

これにより、コントロール変数を無視して、私たちのマーケティングの努力からの売上の合計が得られます。この数値は3,584,648.73 €で、私たちはメディア支出を変更してこれを増やしたいと思っています！ネタバレ：数値は約150万ユーロ増えて5,054,070.21 €になります。素晴らしい！数値を変更するだけで、これだけの成果を上げることができます。

CVXPYでのモデルの再実装

さて、cvxpyを使用して最適解にたどり着く準備が整いました。まず、変数を定義します。チャネルごとに1つずつ、さらに各タイムステップごとに1つずつ変数を定義しますので、合計で3 * N = 3 * 200 = 600の変数があります。

何もない場合、最適解はすべての変数を無限大に設定することになりますので、いくつかの制約が必要です。変数はすべて

1. 非負であること、および
2. これらの600の変数の合計が過去に使った予算以下であること

次に、numpy関数を使用して実装したモデルを最適化したいのですが、そのためには通常、npの代わりにcpを使用して書く必要があります。以前のキャリーオーバーマトリックスを再利用することさえできます！

import cvxpy as cp
original_total_spends = data[["TV", "Radio", "Banners"]].sum().sum()
# 最適化する変数を宣言します。チャネルごとにN=200個
tv = cp.Variable(N)
radio = cp.Variable(N)
banners = cp.Variable(N)
# 制約条件、正の予算と上限付きの合計予算
constraints = [
    tv >= 0,
    radio >= 0,
    banners >= 0,
    cp.sum(tv + radio + banners) <= original_total_spends,
]
# cvxpyの形式、モデルはnumpyバージョンと同様です
problem = cp.Problem(
    cp.Maximize(
        tv_coef * cp.sum(1 - cp.exp(-tv_saturation * tv_carryover_matrix @ tv)) \
        + radio_coef * cp.sum(1 - cp.exp(-radio_saturation * radio_carryover_matrix @ radio)) \
        + banners_coef * cp.sum(1 - cp.exp(-banners_saturation * banners_carryover_matrix @ banners))
    ), # numpyモデルと同様に、全売上の合計
    constraints)

これで最大化問題を非常に短時間で解くことができます。

problem.solve()
# 出力：
# 5054070.207463957

素晴らしい！最適な予算はtv.value, radio.value, banners.valueを使用して取得できます。各週の各チャネルの予算はほぼ一定であることがわかりますが、これは予想ほど興味深くないかもしれません。しかし、最適なものは最適なので、受け入れます。

過去に360万ユーロではなく500万ユーロを得ることができました。これは知っているという点では良いことですが、今は無価値であり、ビジネスを不安にさせるだけかもしれません。ただし、このロジックを使用して将来のマーケティング予算を最適化することもできます！

さらなる制約条件

これで、基本的な予算最適化ツールを持っています！さらに、ビジネスから来るかもしれないさらなる制約条件をモデル化することもできます。例えば、ビジネスが合計のラジオ予算が非常に高いと考えているかもしれません：

sum(radio.value)# 出力: 524290.3686626207 (= 524,290.37 €)

ビジネスは、これを30万ユーロ未満にしたいと言っていますが、これはモデルが知ることができない戦略的な理由です。問題ありません、制約条件に追加しましょう！

constraints = [
    tv >= 0,
    radio >= 0,
    banners >= 0,
    cp.sum(tv + radio + banners) <= original_total_spends,
    cp.sum(radio) <= 300000 # 新しい制約条件
]

これで制約条件を追加しました。最適化を再実行すると、少し減少した最適化された売上が4,990,178.80€となります。しかし、ラジオ予算の合計を確認すると

sum(radio.value)# 出力: 299999.9992275703

ビジネスの制約条件が守られていることがわかります。さらに、以下のような制約条件を追加することもできます。

• 2つのチャネルの合計がある数値より小さいか大きい場合、または
• 一部の週ではメディアの支出を許可しない場合

いくつかの合計と等式または不等式を使用してモデル化するだけです。

結論

この記事では、まずマーケティングミックスモデルの数式を復習しました。これは、モデルを再実装するために必要でした。幸いにも、私たちのモデルは簡単で解釈可能なので、これは全く問題ありませんでした。

実際、私たちのモデルにはもう一つ素晴らしい特性がありました。それは凸であるということです！この場合、売上の最大値は一意に定義されており、凸最適化を通じてそれに到達することができました。非凸または非凸関数の最適化は一般的に困難であり、多くのハイパーパラメータの調整を必要とする芸術的な側面があります。それが私たちがこの方法を選ばなかった理由です。

壮大なフィナーレとして、私たちはメディア予算の最適化を行いました！それは待ち望んでいたことです。私たちはさらに、いくつかのチャネルに最小または最大の予算配分が必要な制約をモデルに組み込む方法も見てきました。このアプローチを使用すると、将来のメディア予算の割り当てを最適化することができます。

私たちが話していないもう一つの最適化は、特定の最小の売上額を達成したいという制約の下で、メディア予算を最小化することです。つまり、目標を達成するためにできるだけ少ないお金を使います。これはあなた自身でも簡単に実装できます！対照的に、以前は持っている全てのお金を使い、可能な限り多くの販売をしました。

皆さんが今日新しい、興味深い、そして価値あるものを学んでいただけたことを願っています。読んでくださりありがとうございます！

最後に、もし

1. 私が機械学習についてもっと書くのをサポートしたい場合や
2. VoAGIのサブスクリプションを取得する予定がある場合は、

なぜこのリンクを経由して やらないのでしょうか ？それは私をとても助けることになります！ 😊

透明性を持って言うと、あなたの価格は変わりませんが、サブスクリプション料金の約半分が直接私に支払われます。

サポートを検討していただける場合は、本当にありがとうございます！

ご質問がありましたら、LinkedInでご連絡ください！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!