類似検索、パート7 LSHの組み合わせ

LSHの組み合わせ

組み合わせによるLSH関数の探索を深掘りし、より信頼性のある検索を確保する

類似性検索は、与えられたクエリに対して、データベース内のすべてのドキュメントの中からそれに最も類似したドキュメントを見つけることを目的とする問題です。

はじめに

データサイエンスでは、類似性検索はNLPの領域や検索エンジン、レコメンデーションシステムなどで頻繁に使用され、クエリに対して最も関連性の高いドキュメントやアイテムを取得する必要があります。大量のデータの中で検索性能を向上させるためのさまざまな方法が存在します。

この記事シリーズの前回の2つのパートでは、LSH（局所センシティブハッシング）について詳しく見てきました。LSHは、入力ベクトルを低次元のハッシュ値に変換しながら、それらの類似性に関する情報を保持するアルゴリズムです。特に、異なる距離指標に適した2つのアルゴリズムをすでに見てきました。

• 相互に接続された複数ページのStreamlitアプリを作成する方法
• 「データガバナンスチームを改善するための4つの革命的な方法」
• 「Pandas：データをワンホットエンコードする方法」

類似性検索、パート5：局所センシティブハッシング（LSH）

類似性情報をハッシュ関数に組み込む方法を調査する

towardsdatascience.com

クラシックなLSHアルゴリズムは、ベクトルのJaccard指数に関する情報を反映したシグネチャを構築します。

類似性検索、パート6：LSHフォレストによるランダムプロジェクション

データをハッシュ化し、ランダムなハイパープレーンを構築することで類似性を反映させる方法を理解する

towardsdatascience.com

ランダムプロジェクションの方法は、ベクトルのコサイン類似度を保持するハイパープレーンのフォレストを構築します。

実際に、LSHアルゴリズムは他の距離指標に対しても存在します。それぞれのメソッドには独自の部分がありますが、それぞれに共通する概念や式が多く存在します。将来的に新しいメソッドを学習するための学習プロセスを容易にするために、基本的なLSHスキームを単純に組み合わせるだけでより複雑なLSHスキームを構築できるようにします。

ボーナスとして、最後にユークリッド距離をLSHに組み込む方法についても見てみましょう。

注意：この記事シリーズのパート5とパート6については、すでに読んでいることが前提とされています。もしまだ読んでいない場合は、まずそれらを読むことを強くおすすめします。

注意：コサイン距離は形式的には範囲[0, 2]で定義されています。簡単のために、[0, 1]の範囲にマッピングします。ここで、0と1はそれぞれ最も低い類似度と最も高い類似度を示します。

形式的なLSHの定義

距離指標dが与えられた場合、Hが(d₁, d₂, p₁, p₂)-sensitive LSH関数と呼ばれる場合、ランダムに選ばれたオブジェクトxとyに対して、以下の条件が満たされる：

• もし d(x, y) ≤ d₁ ならば、p(H(x) = H(y)) ≥ p₁ つまり、確率p₁以上で H(x) = H(y) となる。
• もし d(x, y) ≥ d₂ ならば、p(H(x) = H(y)) ≤ p₂ つまり、確率p₂以下で H(x) = H(y) となる。

これらの文が何を意味するのかを理解しましょう。2つのベクトルが類似している場合、それらの間の距離は低くなります。基本的に、最初の文は、それらを同じバケットにハッシュする確率がある一定の閾値以上であることを確認します。これにより、いくつかの誤検知が排除されます。つまり、2つのベクトル間の距離がd₁よりも大きい場合、それらが同じバケットにハッシュされる確率は常にp₁よりも小さくなります。逆に、2つのベクトルが類似していない場合で、それらの間の距離がd₂よりも大きい場合、同じバケットに現れる確率は上限p₂です。

上記の文に基づいて、通常、システム内の次の文が満たされることを期待します：

• p₁はできるだけ1に近くなるようにし、偽陰性の数を減らします。
• p₂はできるだけ0に近くなるようにし、偽陽性の数を減らします。
• d₁とd₂の間のギャップをできるだけ小さくし、データの確率的な推定ができない間隔を減らします。

時には、上記の文は距離dの代わりに類似度sの用語を使用して紹介されます：

類似度メトリックsが与えられた場合、ランダムに選択されたオブジェクトxとyに対して、以下の条件を満たすとき、Hは(s₁、s₂、p₁、p₂)-感度LSH関数と呼ばれます：

• s(x, y) ≥ s₁の場合、p(H(x) = H(y)) ≥ p₁、つまりH(x) = H(y)となる確率は少なくともp₁です。
• s(x, y) ≤ s₂の場合、p(H(x) = H(y)) ≤ p₂、つまりH(x) = H(y)となる確率は最大でp₂です。

注：この記事では、(d₁、d₂、p₁、p₂)および(s₁、s₂、p₁、p₂)の両方の表記が使用されます。テキストの表記に使用される文字に基づいて、距離dまたは類似度sが示されているかが明確になります。デフォルトでは、表記(d₁、d₂、p₁、p₂)が使用されます。

LSHの例

より明確にするために、次の文を証明しましょう：

距離メトリックsがJaccard指数の場合、Hは(0.6、0.6、0.4、0.4)-感度LSH関数です。基本的には、以下の等価な文が証明されなければなりません：

• d(x, y) ≤ 0.6の場合、p(H(x) = H(y)) ≥ 0.4
• d(x, y) ≥ 0.6の場合、p(H(x) = H(y)) ≤ 0.4

この記事シリーズの第5部で、2つのバイナリベクトルの等しいハッシュ値を取得する確率は、Jaccard類似度と等しいことを知っています。したがって、2つのベクトルが40%以上類似している場合、等しいハッシュ値を取得する確率も少なくとも40%以上であることが保証されます。一方、40%以上のJaccard類似度は、最大で60%のJaccard指数と等価です。結果として、最初の文が証明されます。2番目の文についても同様の考察ができます。

この例は次の定理に一般化できます：

定理。dがJaccard指数の場合、Hは(d₁、d₂、1-d₁、1-d₂)-LSH関数の族です。

同様に、パート6で得られた結果に基づいて、別の定理を証明することが可能です:

定理。sがコサイン類似度で（-1から1の間であるならば）、Hは(s₁、s₂、1 – arccos(s₁) / 180、1 – arccos(d₂) / 180)のLSH関数のファミリーです。

LSH関数の結合

前のパートで学んだLSHの有用な概念について言及しましょう:

• パート5のminhashingに戻ると、すべてのベクトルはいくつかのバンドに分割され、それぞれのバンドには一致する行のセットが含まれていました。ベクトルのペアが候補として考慮されるためには、少なくとも1つのバンドで、ベクトルのすべての行が等しい必要があります。
• パート6のランダムプロジェクションに関しては、初期のベクトルを分離しないランダムプロジェクションがすべて存在する場合にのみ、2つのベクトルが候補として考慮されました。

これら2つのアプローチは、裏側に類似したパラダイムを持っています。両方のアプローチでは、ベクトルのペアが候補として考慮されるのは、n回の構成のうち少なくとも1回、ベクトルがすべてのk回で同じハッシュ値を持つ場合のみです。ブール代数の表記では、次のように書くことができます:

この例に基づいて、ハッシュ関数の集合を集約するための論理演算子ORとANDを紹介しましょう。そして、それらが2つのベクトルが候補である確率と誤りの偽陰性と偽陽性の割合にどのように影響するかを推定します。

AND演算子

n個の独立したLSH関数H₁、H₂、… Hₙが与えられた場合、AND演算子は2つのベクトルを候補のペアとして考慮するのは、両方のベクトルのn個の対応するハッシュ値がすべて等しい場合のみです。それ以外の場合、ベクトルは候補として考慮されません。

2つの非常に異なるベクトルのハッシュ値がAND演算子によって集約される場合、使用されるハッシュ関数の数の増加に伴い、それらが候補である確率は減少します。したがって、偽陽性の数は減少します。

同時に、似たような2つのベクトルが偶然に異なるハッシュ値のペアになる可能性があります。そのため、そのようなベクトルはアルゴリズムによって類似とは見なされません。この側面は、偽陰性の割合が高くなります。

定理。r個の独立した(s₁、s₂、p₁、p₂)-感度LSH関数を考える。これらのr個のLSH関数をAND演算子で組み合わせると、パラメータが次のような新しいLSH関数が得られます:

全てのイベントが発生する確率を推定するために、複数の独立したイベントの確率の積を使用する確率の公式を使用して、この主張を簡単に証明することができます。

OR演算子

n個の独立したLSH関数H₁、H₂、… Hₙが与えられた場合、OR演算子は2つのベクトルを候補のペアとして考慮するのは、両方のベクトルのn個の対応するハッシュ値のうち少なくとも1つが等しい場合のみです。それ以外の場合、ベクトルは候補として考慮されません。

AND演算子とは逆に、OR演算子は2つのベクトルが候補である確率を増加させます。任意のベクトルのペアに対して、対応するハッシュ値の少なくとも1つの等号が十分です。そのため、ORの集約は偽陰性の数を減少させ、偽陽性の数を増加させます。

定理。b個の独立した(d₁、d₂、p₁、p₂)-ファミリーLSH関数を考える。これらのb個のLSH関数をAND演算子で組み合わせると、パラメータが次のような新しいLSH関数が得られます:

この定理を証明することはしません。なぜなら、この記事シリーズのパート5で得られた類似の確率式が説明されているからです。

組み合わせ

ANDとORの操作を持つことで、偽陽性率と偽陰性率をより制御するためにそれらをさまざまな方法で組み合わせることができます。ANDコンビネータによって使用されるr個のLSH関数と、ORコンビネータによって使用されるb個のLSH関数を想像してみましょう。これらの基本的なコンビネータを使用して、2つの異なる組み合わせを構築することができます。

2つ前の記事で説明されたアルゴリズムはAND-ORの組み合わせを使用しています。実際、ANDとORの操作を基にしたより複雑な組み合わせを構築することも可能です。

組み合わせの例

ANDとORの組み合わせがどのようにパフォーマンスを大幅に向上させるかを理解するために、例を研究しましょう。パラメータb=4およびr=8を持つOR-ANDの組み合わせを想定してみましょう。上記の対応する式に基づいて、組み合わせ後の2つのベクトルが候補である初期確率がどのように変化するかを推定することができます。

たとえば、2つのベクトル間の類似度の特定の値に対して、単一のLSH関数が40％の場合に同じバケットにハッシュされるとすると、OR-ANDの組み合わせ後では32.9％の場合にハッシュされるようになります。

組み合わせについて特別な点があるかを理解するために、(0.4, 1.7, 0.8, 0.2)-sensitive LSH関数を考えてみましょう。OR-AND変換後、LSH関数は(0.4, 1.7, 0.0148, 0.987)-sensitive形式に変換されます。

本質的には、最初に2つのベクトルが非常に類似しており、距離が0.4未満である場合、それらは80％のケースで候補と見なされます。しかし、組み合わせが適用されると、それらは98.7％のシナリオで候補となり、誤りの少ないネガティブエラーが発生します！

同様に、2つのベクトルがお互いに非常に異なり、距離が1.7よりも大きい場合、それらは現在、1.48％のケースでのみ候補と見なされます（以前の20％と比較して）。これにより、偽陽性エラーの頻度が13.5倍減少します！これは非常に大きな改善です！

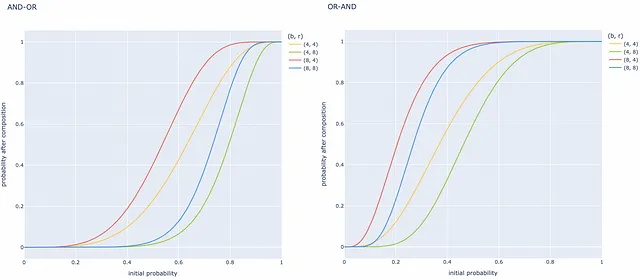
一般的には、(d₁, d₂, p₁, p₂)-sensitive LSH関数を持つことで、(d₁, d₂, p’₁, p’₂)の形式に変換することができます。ここで、p’₁は1に近く、p’₂は0に近くなります。1に近づくためには、通常、より多くの組み合わせを使用する必要があります。

他の距離メトリックに対するLSH

Jaccard指数やコサイン距離の情報を保持するために使用されるLSHスキームについてはすでに詳しく調査しました。次に自然に浮かぶのは、他の距離メトリックに対してLSHアルゴリズムを使用できるかどうかです。残念ながら、ほとんどのメトリックには対応するLSHアルゴリズムが存在しません。

ただし、機械学習でよく使用されるメトリックの1つであるユークリッド距離にはLSHスキーマが存在します。頻繁に使用されるため、ユークリッド距離のハッシュ値を取得する方法を研究します。上記で導入した理論的な表記を使用して、このメトリックに対する重要なLSHの特性を証明します。

ユークリッド距離のためのLSH

ユークリッド空間における点のハッシュ化メカニズムは、ランダムな直線上に射影することを含みます。アルゴリズムは以下を仮定します。

• 2つの点が比較的近い場合、それらの射影も近いはずです。
• 2つの点が遠い場合、それらの射影も遠いはずです。

2つの射影がどれだけ近いかを測るために、直線をいくつかの等しいセグメント（バケット）に分割することができます。各直線セグメントは特定のハッシュ値に対応しています。2つの点が同じ直線セグメントに射影される場合、それらは同じハッシュ値を持ちます。それ以外の場合、ハッシュ値は異なります。

この方法は初めは頑健に見えるかもしれませんが、依然として互いに遠い点を同じセグメントに射影することがあります。特に、2つの点を結ぶ直線が初期射影直線にほぼ垂直な場合に起こります。

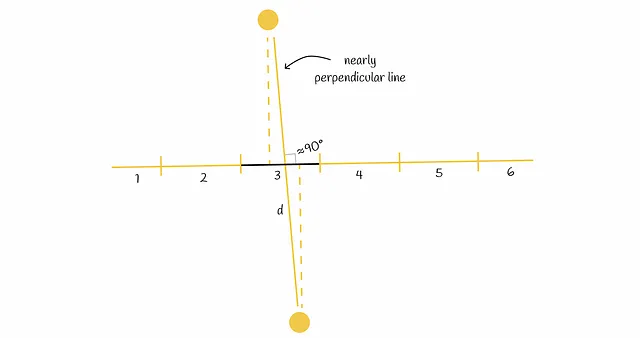
エラーレートを減らすためには、上記で議論されたランダム射影直線の組合せを使用することを強くお勧めします。

ユークリッド空間において単一の直線セグメントの長さがaである場合、Hは(a / 2, 2a, ½, ⅓)-sensitive LSH関数であることを幾何学的に証明することが可能です。

結論

この章では、一般的なLSH記法に関する知識を蓄積し、組合せ操作を形式的に導入することでエラーレートを大幅に削減することができました。LSHは機械学習メトリクスの一部にしか存在しないことに注意する価値がありますが、少なくともユークリッド距離、コサイン距離、ジャカード指数などの最も人気のあるメトリクスには存在します。ベクトル間の類似性を測る別のメトリクスを扱う場合には、別の類似性検索手法を選択することが推奨されます。

この記事で紹介された文の形式的な証明については、以下のノートで見つけることができます。

リソース

• 局所性鋭敏ハッシング | ビッグデータアナリティクスの講義ノート | Nimrah Mustafa
• コサイン距離 | Wikipedia

すべての画像は、特に記載がない限り、著者によるものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!