「ロジスティック回帰：直感と実装」

Logistic Regression Intuition and Implementation

ロジスティック回帰アルゴリズムの数学とNumpyを使った実装について

はじめに

ロジスティック回帰は、2つの異なるデータ属性の間の決定境界を学習することができる基本的な二値分類アルゴリズムです。この記事では、分類モデルの理論的な側面を理解し、Pythonを使用して実装します。

直感

データセット

ロジスティック回帰は教師あり学習アルゴリズムなので、データの特徴属性とそれに対応するラベルがあります。特徴は独立変数であり、Xで表され、1次元配列で表されます。クラスラベルはyで表され、0または1です。したがって、ロジスティック回帰は二値分類アルゴリズムです。

データにd個の特徴がある場合:

• このAI論文は、拡散モデル内のコンセプトニューロンを分析および識別するための、コーンと呼ばれる新しい勾配ベースの手法を提案しています
• 「圧縮が必要ですか？」
• 「CLAMPに会ってください：推論時に新しい実験に適応できる分子活性予測のための新しいAIツール」

コスト関数

線形回帰と同様に、特徴属性に関連する重みとバイアス値があります。

私たちの目標は、重みとバイアスの最適な値を見つけて、データによりよくフィットさせることです。

各特徴属性には重み値が、単一のバイアス値が関連付けられています。

これらの値をランダムに初期化し、勾配降下法を使用して最適化します。トレーニング中に、重みと特徴の内積を取り、バイアス項を追加します。

しかし、ターゲットラベルが0と1であるため、必要な範囲内に値を押し込む非線形シグモイド関数gを使用します。

プロットされたシグモイド関数は次のようになります:

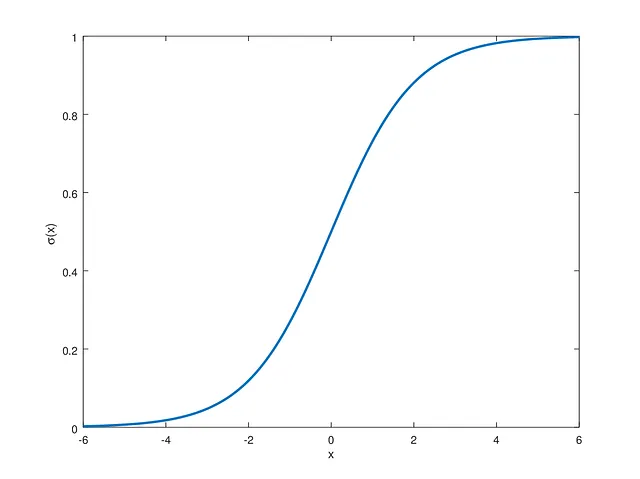
ロジスティック回帰は、シグモイド関数に渡される値が正の場合に正のラベルに、負の場合に負のラベルになるように重みとバイアスを学習することを目指しています。

ロジスティック回帰で値を予測するために、予測をシグモイド関数に渡します。したがって、予測関数は次のようになります:

モデルから予測を取得したので、それらを元のターゲットラベルと比較することができます。予測間のエラーは、バイナリクロスエントロピー損失を使用して計算されます。損失関数は次のようになります:

ここで、yは元のターゲットラベルであり、pは[0,1]の範囲内の予測値です。損失関数は、予測値を実際のターゲットラベルに近づけることを目指しています。ラベルが0であり、モデルが0を予測する場合、損失は0です。同様に、予測されたラベルが1である場合も損失は0です。それ以外の場合、モデルはこれらの値に収束しようとします。

勾配降下法

コスト関数を使用して、重みとバイアスに関する微分を得ます。連鎖律と数学的な導出を使用して、導関数は次のようになります:

重みとバイアスを更新するために使用できるスカラー値を取得します。

これにより、損失勾配に対して値が更新され、複数の反復を経ることで重みとバイアスの最適な値に徐々に収束します。

推論時には、重みとバイアスの値を使用して予測することができます。

実装

上記の数式を使用して、ロジスティック回帰モデルをコーディングし、いくつかのベンチマークデータセットで性能を評価します。

まず、クラスとパラメータを初期化します。

class LogisticRegression():    def __init__(            self,            learning_rate:float=0.001,            n_iters:int=10000        ) -> None:        self.n_iters = n_iters        self.lr = learning_rate                self.weights = None        self.bias = None

最適化される重みとバイアスの値が必要なので、ここでオブジェクト属性として初期化します。ただし、ここではデータによってサイズが決まるため、一旦Noneに設定します。学習率と反復回数は、パフォーマンスを調整するためのハイパーパラメータです。

トレーニング

def fit(        self,        X : np.ndarray,         y : np.ndarray    ):        n_samples, n_features = X.shape                # Initialize Weights and Bias with Random Values        # Size of Weights matirx is based on the number of data features        # Bias is a scalar value        self.weights = np.random.rand(n_features)        self.bias = 0                for iteration in range(self.n_iters):                        # Get predictions from Model            linear_pred = np.dot(X, self.weights) + self.bias            predictions = sigmoid(linear_pred)                        loss = predictions - y                        # Gradient Descent based on Loss            dw = (1 / n_samples) * np.dot(X.T, loss)            db = (1 / n_samples) * np.sum(loss)                    # Update Model Parameters            self.weights = self.weights - self.lr * dw            self.bias = self.bias - self.lr * db

トレーニング関数は、重みとバイアスの値を初期化します。その後、データセットを複数回反復して、これらの値を収束に向かって最適化し、損失が最小化されるようにします。

上記の方程式に基づいて、シグモイド関数は以下のように実装されます：

def sigmoid(x):    return 1 / (1 + np.exp(-x))

次に、この関数を使用して次のように予測を生成します：

linear_pred = np.dot(X, self.weights) + self.biaspredictions = sigmoid(linear_pred)

これらの値に対して損失を計算し、重みを最適化します：

loss = predictions - y            # Gradient Descent based on Lossdw = (1 / n_samples) * np.dot(X.T, loss)db = (1 / n_samples) * np.sum(loss)# Update Model Parametersself.weights = self.weights - self.lr * dwself.bias = self.bias - self.lr * db

推論

def predict(        self,        X : np.ndarray,        threshold:float=0.5    ):        linear_pred = np.dot(X, self.weights) + self.bias        predictions = sigmoid(linear_pred)                # Convert to 0 or 1 Label         y_pred = [0 if y <= threshold else 1 for y in predictions]                return y_pred

トレーニング中にデータをフィットさせた後、学習した重みとバイアスを使用して同様に予測を生成できます。モデルの出力は、シグモイド関数に従って範囲[0, 1]になります。その後、0.5などのしきい値を使用します。この確率以上の値は正のラベルとしてタグ付けされ、このしきい値未満の値は負のラベルとしてタグ付けされます。

完全なコード

import numpy as npdef sigmoid(x):    return 1 / (1 + np.exp(-x))class LogisticRegression():    def __init__(            self,            learning_rate:float=0.001,            n_iters:int=10000        ) -> None:        self.n_iters = n_iters        self.lr = learning_rate                self.weights = None        self.bias = None        def fit(        self,        X : np.ndarray,         y : np.ndarray    ):        n_samples, n_features = X.shape                # Initialize Weights and Bias with Random Values        # Size of Weights matirx is based on the number of data features        # Bias is a scalar value        self.weights = np.random.rand(n_features)        self.bias = 0                for iteration in range(self.n_iters):                        # Get predictions from Model            linear_pred = np.dot(X, self.weights) + self.bias            predictions = sigmoid(linear_pred)                        loss = predictions - y                        # Gradient Descent based on Loss            dw = (1 / n_samples) * np.dot(X.T, loss)            db = (1 / n_samples) * np.sum(loss)                    # Update Model Parameters            self.weights = self.weights - self.lr * dw            self.bias = self.bias - self.lr * db                def predict(        self,        X : np.ndarray,        threshold:float=0.5    ):        linear_pred = np.dot(X, self.weights) + self.bias        predictions = sigmoid(linear_pred)                # Convert to 0 or 1 Label         y_pred = [0 if y <= threshold else 1 for y in predictions]                return y_pred

評価

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer
from sklearn.metrics import accuracy_score
from model import LogisticRegression

if __name__ == "__main__":
    data = load_breast_cancer()
    X, y = data.data, data.target
    
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=True)
    
    model = LogisticRegression()
    model.fit(X_train, y_train)
    
    y_pred = model.predict(X_test)
    score = accuracy_score(y_pred, y_test)
    
    print(score)

上記のスクリプトを使用して、ロジスティック回帰モデルをテストすることができます。トレーニングにはScikit-Learnから提供される乳がんデータセットを使用します。予測結果と元のラベルを比較することができます。

いくつかのハイパーパラメータを注意深く調整することで、90%以上の正解率を得ることができました。

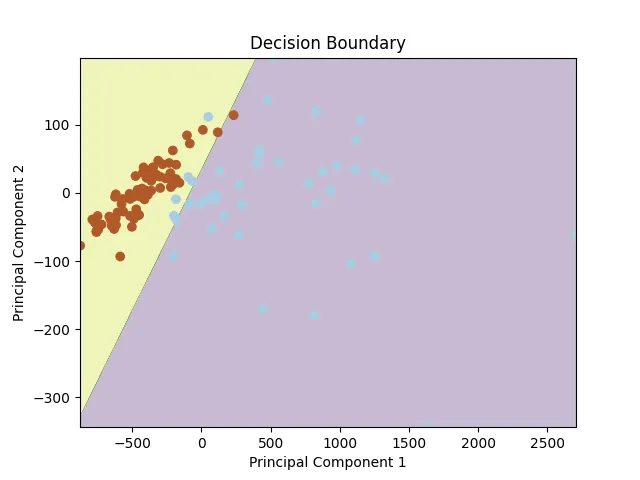
PCAなどの異なる次元削減技術を使用して、決定境界を視覚化することができます。特徴量を2次元に削減した後、以下のような決定境界が得られます。

結論

まとめると、この記事ではロジスティック回帰の数学的な直感を探求し、NumPyを使用した実装を示しました。ロジスティック回帰は、シグモイド関数と勾配降下法を利用して、2値分類のための最適な決定境界を見つけるための貴重な分類アルゴリズムです。

コードと実装については、このGitHubリポジトリを参照してください。ディープラーニングアーキテクチャや研究の最新情報については、私のフォローをお願いします。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!