物理情報を組み込んだDeepONetによるオペレータ学習 ゼロから実装しましょう

Let's implement operator learning from scratch using DeepONet with incorporated physical information.

DeepONets、物理情報を組み込んだニューラルネットワーク、および物理情報を組み込んだDeepONetsの詳細について

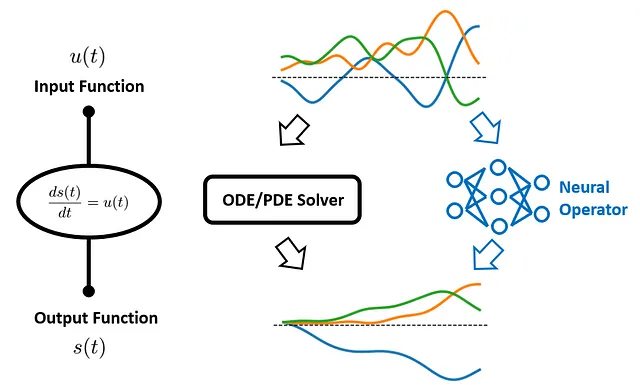
普通微分方程式（ODE）および偏微分方程式（PDE）は、物理学や生物学から経済学や気候科学まで、科学と工学の多くの分野で骨幹を成すものです。これらは、連続的に変化する量を時間と空間にわたって捉えるために使用される基本的なツールです。

しかし、これらの方程式の特徴的な点の1つは、単一の値だけでなく関数を入力として受け取ることです。たとえば、建物の地震による振動を予測する場合を考えてみましょう。地面の揺れは時間とともに変化するため、建物の運動を記述する微分方程式への入力として機能する関数で表すことができます。同様に、コンサートホールで伝播する音波の場合、楽器によって生成される音波は時間とともに音量とピッチが変化する入力関数となります。これらの変化する入力関数は、結果として得られる出力関数、つまり建物の振動やホール内の音響場に基本的な影響を与えます。

従来、これらのODE/PDEは有限差分法や有限要素法などの数値ソルバーを使用して対処されてきました。しかし、この方法にはボトルネックがあります。新しい入力関数ごとに、ソルバーを再実行する必要があります。このプロセスは計算量が多く、特に複雑なシステムや高次元の入力に対しては遅いです。

この課題に対処するために、2019年にLuらによって新しいフレームワークが導入されました：Deep Operator Network（DeepONet）。DeepONetは、入力関数を出力関数にマッピングするオペレータを学習することを目指しています。つまり、数値ソルバーを再実行することなく、任意の入力関数に対するこれらのODE/PDEの出力を予測することを学習します。

• OpenAIのモデレーションAPIを使用してコンテンツのモデレーションを強化する
• 50以上の機械学習面接（インタビュアーとして）から学んだこと
• 最初のマシンアンラーニングチャレンジを発表します

しかし、DeepONetは強力ですが、データ駆動型の手法が直面する一般的な問題を引き継いでいます。ガバニング方程式に内包される既知の物理法則と予測の整合性をどのように保証できるでしょうか？

それには物理情報を組み込んだ学習が登場します。

物理情報を組み込んだ学習は、複雑な物理システムのモデリングと理解を向上させるために、物理原理とデータサイエンスを組み合わせた急速に発展している機械学習の一分野です。これには、ドメイン固有の知識と物理法則を活用して学習プロセスをガイドし、機械学習モデルの正確性、汎化性、解釈性を向上させることが含まれます。

このフレームワークの下で、2021年にWangらはDeepONetの新しいバリアントを導入しました：物理情報を組み込んだDeepONet。この革新的なアプローチは、DeepONetの基盤を活用しながら、学習プロセスに物理法則の理解を組み込んでいます。もはやモデルにデータから学習するだけではありません。数世紀にわたる科学的研究から導かれた原則でモデルをガイドしています。

これは非常に有望なアプローチのようです！しかし、実際にはどのように実装すればよいのでしょうか？今日はそれを詳しく探ってみましょう 🤗

このブログでは、物理情報を組み込んだDeepONetの理論について説明し、ゼロから実装する方法を説明します。また、開発したモデルを実際に使用し、ハンズオンのケーススタディを通じてそのパワーを実証します。

さあ、始めましょう！

目次 · 1. ケーススタディ · 2. 物理情報を組み込んだDeepONet ∘ 2.1 DeepONetの概要 ∘ 2.2 物理情報を組み込んだニューラルネットワーク（PINNs） ∘ 2.3 物理情報を組み込んだDeepONet · 3. 物理情報を組み込んだDeepONetの実装 ∘ 3.1 アーキテクチャの定義 ∘ 3.2 ODE損失の定義 ∘ 3.3 勾配降下法のステップの定義 · 4. データの生成と組織化 ∘ 4.1 u(·)プロファイルの生成 ∘ 4.2 データセットの生成 ∘ 4.3 データセットの組織化 · 5. 物理情報を組み込んだDeepONetのトレーニング · 6. 結果の議論 · 7. 要点 · 参考文献

1. ケーススタディ

具体的な例で議論を展開しましょう。このブログでは、Wang et al.のオリジナル論文で考慮された最初のケーススタディを再現します。すなわち、次の常微分方程式（ODE）によって記述される初期値問題です：

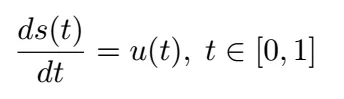
初期条件 s(0) = 0 であるとします。

この方程式では、u( t ) は時間によって変化する入力関数であり、s( t ) は時間 t におけるシステムの状態で、予測したいものです。物理的なシナリオでは、u( t ) はシステムに加えられた力を表し、s( t ) はコンテキストに応じて変位や速度などのシステムの応答を表すかもしれません。ここでの目標は、強制項 u( t ) と ODE の解 s( t ) のマッピングを学習することです。

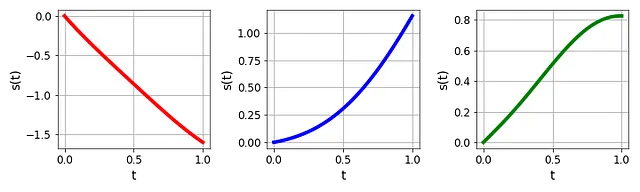
オイラー法やルンゲ・クッタ法などの従来の数値計算法は、この方程式を効果的に解くことができます。しかし、強制項 u( t ) は次の図に示すように、さまざまなプロファイルを持つことに注意してください：

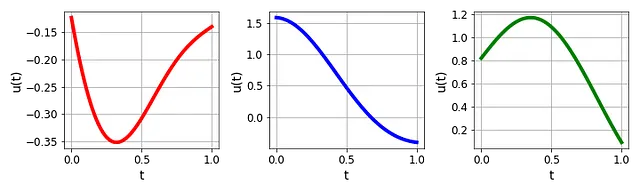
そのため、u( t ) が変化するたびに、対応する s( t ) を再計算する必要があります（図3参照）。これは計算負荷が大きく非効率的な場合があります。

では、このような問題をより効率的に解決するにはどうすればよいでしょうか？

2. 物理情報のある DeepONet

前述のように、物理情報のある DeepONet は、私たちの目標の問題に有望な解決策を提供します。このセクションでは、その基本的な概念を理解しやすく解説します。

まず、元の DeepONet の基本原理について説明します。それに続いて、物理情報を持つニューラルネットワークの概念と、それが問題解決のテーブルにもたらす追加の次元について探求します。最後に、これら二つのアイデアをシームレスに統合して物理情報のある DeepONet を構築する方法を示します。

2.1 DeepONet の概要

DeepONet（Deep Operator Network）は、ディープラーニングの新たなフロンティアを代表します。従来の機械学習方法が一連の入力値を出力値にマップするのに対し、DeepONet は関数全体を他の関数にマッピングするように設計されています。これにより、機能的な入力と出力が自然に関与する問題において、DeepONet は特に強力です。では、具体的にどのようにその目標を達成するのでしょうか？

我々が象徴的に達成したいことを数式で表すと：

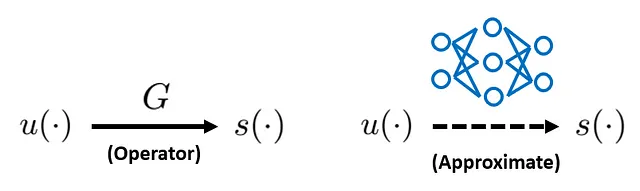
左側には、入力関数 u(·) から出力関数 s(·) へのオペレータ G があります。右側では、ニューラルネットワークを使ってオペレータ G を近似したいと考えています。この目標を達成できれば、訓練されたニューラルネットワークを使って任意の u(·) に対して s(·) の高速な計算が行えるようになります。

現在のケーススタディでは、入力関数 u(·) と出力関数 s(·) は時間座標 t を唯一の引数として取ります。したがって、構築するニューラルネットワークの「入力」と「出力」は次のようになる必要があります：

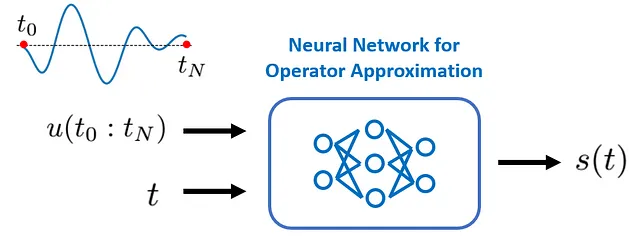
基本的に、私たちのニューラルネットワークは、u( t ) の全プロファイルを最初の入力として受け入れ、特定の時間インスタンス t を2番目の入力として受け入れる必要があります。その後、時間インスタンス t で評価される目標出力関数 s(·)、つまり s( t ) を出力する必要があります。

このセットアップをよりよく理解するために、s( t ) の値は、まず s(·) のプロファイルに依存し、そのプロファイルは u(·) に依存し、さらに s(·) が評価される時間インスタンスに依存することに気付きます。これが時間座標 t が入力に含まれる必要がある理由でもあります。

現時点でクリアする必要がある2つの質問があります：まず、連続した u(·) のプロファイルをネットワークにどのように入力すればよいですか？そして、2つの入力、つまり t と u(·) をどのように連結すればよいですか？

1️⃣ 連続した u(·) のプロファイルをどのように入力すればよいですか？

実際には、直接連続したプロファイル u(·) を入力する必要はありません。具体的には、十分な数の場所で u(·) の値を評価し、それらの離散的な u(·) の値をニューラルネットワークに送信するだけです：

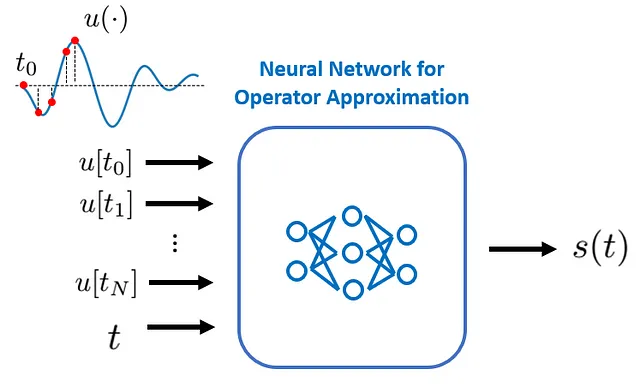
これらの場所は、元の DeepONet 論文では「センサー」と呼ばれています。

2️⃣ 入力 t と u(·) をどのように連結すればよいですか？

一見すると、それらを入力層で直接連結したいと思うかもしれません。しかし、この素朴なアプローチは、使用できるニューラルネットワークの種類に制約を加えるだけでなく、実際の予測精度も劣化させることがわかります。しかし、より良い方法があります。DeepONet を紹介しましょう。

要するに、DeepONet は演算子学習を行うための新しいネットワークアーキテクチャを提案しました：それは2つの主要なコンポーネントで構成されています：ブランチネットワーク と トランクネットワーク 。ブランチネットワークは離散的な関数値を入力として受け取り、それらを特徴ベクトルに変換します。一方、トランクネットワークは座標（現在のケーススタディでは座標はただの t です。PDEの場合は時間座標と空間座標の両方が含まれます）を受け取り、同じ次元の特徴ベクトルに変換します。これらの2つの特徴ベクトルはドット積によって結合され、その結果が入力座標で評価される s(·) の予測として使用されます。

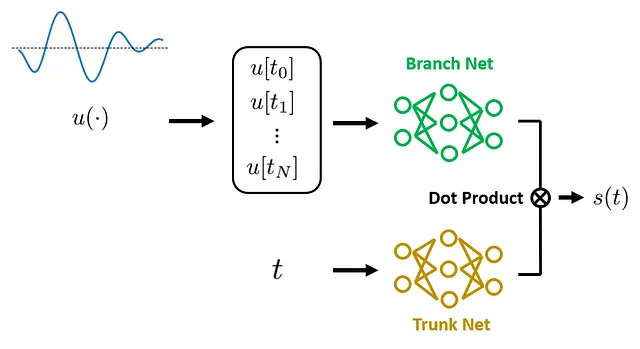
DeepONetの元の論文では、著者はこの「分割統治」戦略について述べており、これは「枝」と「幹」という別々のネットワークで具体化されています。これは、演算子学習のために特に強力な帰納的バイアスを導入するための普遍的な近似定理に触発されたものです。これがDeepONetを効果的な解決策にする鍵となっています。

DeepONetの理論的な基礎についてもっと知りたい場合は、元の論文の付録Aを参照してください。

DeepONetの主な強みの一つは、効率性です。トレーニング後、新しい入力関数の出力関数をリアルタイムで推論することができます。追加のトレーニングは必要ありません。ただし、新しい入力関数がトレーニング時の入力関数の範囲内にある限りです。これにより、DeepONetはリアルタイム推論を必要とするアプリケーションで強力なツールとなります。

DeepONetのもう一つの注目すべき強みは、その柔軟性と多様性です。幹と枝のネットワークの最も一般的な選択肢は完全に接続された層ですが、DeepONetフレームワークでは、高度なアーキテクチャのカスタマイズが可能です。入力関数u(·)と座標の特性に応じて、CNN、RNNなどさまざまなニューラルネットワークアーキテクチャを使用することもできます。この適応性により、DeepONetは非常に多目的なツールとなります。

ただし、これらの強みにもかかわらず、DeepONetの制限も顕著です。純粋なデータ駆動型の手法であるため、DeepONetは予測が事前知識や物理システムを記述する支配方程式に従うことを保証することはできません。その結果、DeepONetは特にトレーニングデータの分布外にある入力関数、つまり分布外（OOD）の入力に直面した場合にはうまく一般化しない場合があります。その一般的な対策は、単にトレーニング用の大量のデータを用意することですが、これは常に実践的ではなく、特にデータの収集が費用や時間がかかる科学やエンジニアリングの分野では実現が難しい場合もあります。

では、これらの制限にどのように対処すべきでしょうか？物理情報学習、具体的には物理情報学習ニューラルネットワーク（PINNs）について話しましょう。

2.2 物理情報学習ニューラルネットワーク（PINNs）

従来の機械学習モデルでは、基礎となるパターンを学習するために主にデータに頼っています。しかし、多くの科学やエンジニアリングの分野では、動的システムに関する事前知識として支配方程式（ODE/PDE）が利用可能であり、観測データ以外の情報源となり得ます。この追加の知識源を正しく組み込むことで、モデルの性能と一般化能力を改善することができます。これが物理情報学習の重要性です。

物理情報学習とニューラルネットワークの概念を組み合わせると、物理情報学習ニューラルネットワーク（PINNs）というものになります。

PINNsは、データにフィットするだけでなく、微分方程式によって記述される既知の物理法則も尊重するようにネットワークをトレーニングするタイプのニューラルネットワークです。これは、支配微分方程式の違反度を測定するODE/PDEロスを導入することで実現されます。このように、物理法則をネットワークのトレーニングプロセスに注入し、物理的に情報を与えます。

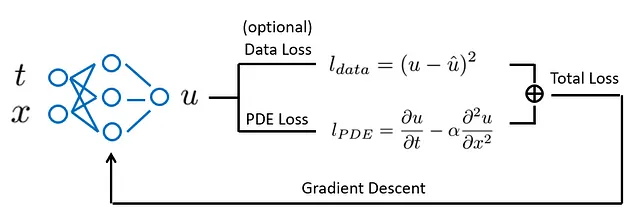
PINNsは多くのアプリケーションで効果的であることが証明されていますが、制限もあります。PINNsは通常、特定の入力パラメータ（境界条件や初期条件、外部強制など）のためにトレーニングされます。したがって、入力パラメータが変更されるたびにPINNを再トレーニングする必要があります。したがって、異なる動作条件でのリアルタイム推論には特に効果的ではありません。

さて、変動する入力パラメータを扱うために特に設計された手法をまだ覚えていますか？そうです、それはDeepONetです！物理情報学習のアイデアをDeepONetと組み合わせる時が来ました。

2.3 物理情報を組み込んだDeepONet

物理情報を組み込んだDeepONetの主なアイデアは、DeepONetとPINNの両方の強みを組み合わせることです。DeepONetと同様に、物理情報を組み込んだDeepONetは関数を入力として受け取り、関数を出力として生成することができます。これにより、再学習の必要なく新しい入力関数のリアルタイム推論が非常に効率的に行えます。

一方、PINNと同様に、物理情報を組み込んだDeepONetは既知の物理法則を学習プロセスに取り込みます。これらの法則は、トレーニング中の損失関数に追加の制約として導入されます。このアプローチにより、モデルは限られたまたはノイズのあるデータを扱う場合でも物理的に整合性のある予測を行うことができます。

この統合をどのように実現するのでしょうか？PINNと同様に、モデルの予測が既知の微分方程式にどれだけ適合しているかを測定するための追加の損失を追加します。この損失関数を最適化することで、モデルはデータに整合し（トレーニング中に計測データが提供された場合）、物理的に整合した予測を行うことを学習します。

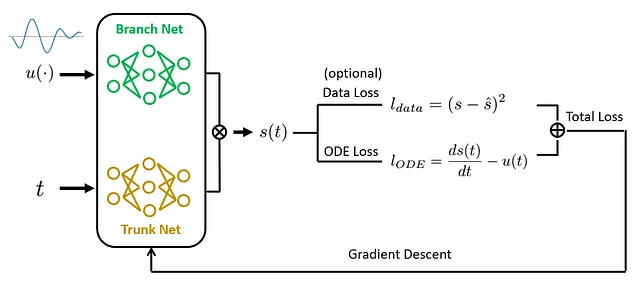
要約すると、物理情報を組み込んだDeepONetは、DeepONetの効率性と物理情報を組み込んだ学習の精度の両方の利点を組み合わせた強力なツールです。リアルタイム推論と物理的な整合性の両方が重要な分野で複雑な問題を解決する有望なアプローチを示しています。

次のセクションでは、ケーススタディに取り組み、理論を実際のコードに変換していきます。

3. 物理情報を組み込んだDeepONetの実装

このセクションでは、対象のケーススタディに対応する物理情報を組み込んだDeepONetモデルの定義方法について説明します。TensorFlowで実装します。まず、必要なライブラリをインポートしましょう：

import numpy as npimport matplotlib.pyplot as pltimport tensorflow as tffrom tensorflow import kerastf.random.set_seed(42)

3.1 アーキテクチャの定義

前述のように、物理情報を組み込んだDeepONetは元のDeepONetと同じアーキテクチャを共有しています。以下の関数はDeepONetのアーキテクチャを定義します：

def create_model(mean, var, verbose=False):    """全結合ブランチとトランク層を持つDeepONetの定義。        Args:    ----    mean: 辞書、入力の平均値    var: 辞書、入力の分散値    verbose: ブール値、モデルの概要を表示するかどうかを示す        Outputs:    --------    model: DeepONetモデル    """        # ブランチネット    branch_input = tf.keras.Input(shape=(len(mean['forcing'])), name="forcing")    branch = tf.keras.layers.Normalization(mean=mean['forcing'], variance=var['forcing'])(branch_input)    for i in range(3):        branch = tf.keras.layers.Dense(50, activation="tanh")(branch)        # トランクネット    trunk_input = tf.keras.Input(shape=(len(mean['time'])), name="time")    trunk = tf.keras.layers.Normalization(mean=mean['time'], variance=var['time'])(trunk_input)       for i in range(3):        trunk = tf.keras.layers.Dense(50, activation="tanh")(trunk)        # ブランチとトランクネットの内積を計算    dot_product = tf.reduce_sum(tf.multiply(branch, trunk), axis=1, keepdims=True)        # バイアスを追加    output = BiasLayer()(dot_product)        # モデルを作成    model = tf.keras.models.Model(inputs=[branch_input, trunk_input], outputs=output)        if verbose:        model.summary()            return model   

上記のコードでは：

1. トランクとブランチのネットワークは、3つの隠れ層を持つ全結合ネットワークであると仮定しています。各層には50個のニューロンがあり、tanh活性化関数が使用されています。このアーキテクチャは予備的なテストに基づいて選ばれたものであり、この問題の良い出発点となるはずです。ただし、他のアーキテクチャ（例：CNN、RNNなど）や他のレイヤーのハイパーパラメータに置き換えることも簡単です。
2. トランクとブランチのネットワークの出力は、内積によってマージされます。元のDeepONetの論文で示唆されているように、予測精度を向上させるためにバイアス項を追加します。 BiasLayer()は、その目標を達成するためにカスタム定義されたクラスです：

class BiasLayer(tf.keras.layers.Layer):    
    def build(self, input_shape):
        self.bias = self.add_weight(shape=(1,), 
                                    initializer=tf.keras.initializers.Zeros(), 
                                    trainable=True)    
    def call(self, inputs):
        return inputs + self.bias

3.2 ODE損失の定義

次に、ODE損失を計算する関数を定義します。ターゲットのODEは次のようになります：

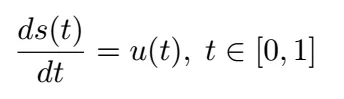
したがって、関数を次のように定義できます：

@tf.functiondef ODE_residual_calculator(t, u, u_t, model):
    """ODEの残差計算。
    Args:
    ----
    t: 時間座標
    u: 離散的な時間座標で評価された入力関数
    u_t: tで評価された入力関数
    model: DeepONetモデル

    Outputs:
    --------
    ODE_residual: 支配するODEの残差
    """
    with tf.GradientTape() as tape:
        tape.watch(t)
        s = model({"forcing": u, "time": t})
        # 勾配の計算
        ds_dt = tape.gradient(s, t)
        # ODEの残差
        ODE_residual = ds_dt - u_t
        return ODE_residual

上記のコードでは：

1. tf.GradientTape()を使用して、s(·)のtに関する勾配を計算しました。TensorFlowでは、tf.GradientTape()はコンテキストマネージャとして使用され、テープのコンテキスト内で実行されたすべての操作がテープに記録されます。ここでは、明示的に変数tを監視するようにしました。その結果、TensorFlowは自動的にtに関わるすべての操作を追跡します。この場合、DeepONetモデルの正順の実行です。その後、テープのgradient()メソッドを使用して、s(·)のtに関する勾配を計算します。
2. 入力引数にu_tを追加しました。これは、tで評価された入力関数u(·)の値を示します。これは、ターゲットODEの右辺の項であり、ODEの残差損失の計算に必要です。
3. 通常のPython関数をTensorFlowグラフに変換するために、@tf.functionデコレータを使用しました。これは、勾配の計算が非常に高コストであり、グラフモードで実行することで計算を大幅に高速化できるため便利です。

3.3 勾配降下法ステップの定義

次に、トータル損失関数をコンパイルし、ネットワークモデルパラメータに対するトータル損失の勾配を計算する関数を定義します：

@tf.functiondef train_step(X, X_init, IC_weight, ODE_weight, model):
    """ネットワークモデルパラメータに対するトータル損失の勾配を計算する。
    Args:
    ----
    X: ODE残差を評価するためのトレーニングデータセット
    X_init: 初期条件を評価するためのトレーニングデータセット
    IC_weight: 初期条件の損失の重み
    ODE_weight: ODEの損失の重み
    model: DeepONetモデル

    Outputs:
    --------
    ODE_loss: 計算されたODE損失
    IC_loss: 計算された初期条件の損失
    total_loss: ODE損失と初期条件の損失の加重和
    gradients: ネットワークモデルパラメータに対するトータル損失の勾配
    """
    with tf.GradientTape() as tape:
        tape.watch(model.trainable_weights)
        # 初期条件の予測
        y_pred_IC = model({"forcing": X_init[:, 1:-1], "time": X_init[:, :1]})
        # 方程式の残差
        ODE_residual = ODE_residual_calculator(t=X[:, :1], u=X[:, 1:-1], u_t=X[:, -1:], model=model)
        # 損失の計算
        IC_loss = tf.reduce_mean(keras.losses.mean_squared_error(0, y_pred_IC))
        ODE_loss = tf.reduce_mean(tf.square(ODE_residual))
        # トータル損失
        total_loss = IC_loss*IC_weight + ODE_loss*ODE_weight
    gradients = tape.gradient(total_loss, model.trainable_variables)
    return ODE_loss, IC_loss, total_loss, gradients

上記のコードでは：

1. 初期条件の損失IC_lossとODE残差の損失ODE_lossの2つの損失項を考慮しています。 IC_lossは、モデル予測のs( t = 0)と既知の初期値0を比較して計算され、ODE_lossは、先に定義したODE_residual_calculator関数を呼び出して計算されます。データの損失も計算してトータル損失に追加できますが、測定されたs( t )の値が利用可能である場合に限ります（上記のコードでは実装されていません）。
2. 一般的に、トータル損失はIC_lossとODE_lossの加重和です。重みは、トレーニングプロセス中に個々の損失項にどれだけの重点や優先度を与えるかを制御します。このケーススタディでは、IC_weightとODE_weightを共に1に設定するだけで十分です。
3. ODE_lossの計算方法と同様に、勾配を計算するためにtf.GradientTape()をコンテキストマネージャとして使用しました。ただし、ここでは、ネットワークモデルパラメータに対するトータル損失の勾配を計算しています。これは、勾配降下法を実行するために必要です。

進む前に、これまでに開発した内容を簡単にまとめましょう：

1️⃣ create_model() 関数を使用して DeepONet モデルを初期化できます。

2️⃣ ODE_residual_calculator 関数を使用して、モデルの予測が支配する ODE にどれだけ適合しているかを評価するための ODE の残差を計算できます。

3️⃣ train_step を使用して、ネットワークモデルパラメータに関する総損失とその勾配を計算できます。

準備作業は半分終わりました🚀 次のセクションでは、データの生成とデータの整理の問題（上記のコードでの奇妙なX[:, :1]）について説明します。その後、モデルをトレーニングしてパフォーマンスを確認することができます。

4. データの生成と整理

このセクションでは、物理情報を持つ DeepONet モデルのトレーニングのために、合成データの生成方法と整理方法について説明します。

4.1 u(·) プロファイルの生成

トレーニング、検証、およびテストに使用するデータは合成的に生成されます。このアプローチの理論的根拠は二つあります：便利であるだけでなく、データの特性を完全に制御することができます。

今回のケーススタディでは、入力関数 u(·) をゼロ平均のガウス過程を使用して、放射基底関数（RBF）カーネルで生成します。

ガウス過程は、機械学習で一般的に使用される強力な数学的フレームワークです。RBFカーネルは、入力点間の類似性を捉えるための人気のある選択肢です。ガウス過程内でRBFカーネルを使用することで、生成された合成データは滑らかで連続的なパターンを示すようになります。これはさまざまなアプリケーションで望ましいことが多いです。Gaussian Processについて詳しくは、以前のブログをご覧ください。

scikit-learnでは、これをわずか数行のコードで実現できます：

from sklearn.gaussian_process import GaussianProcessRegressorfrom sklearn.gaussian_process.kernels import RBFdef create_samples(length_scale, sample_num):    """u(·)の合成データを作成        Args:    ----    length_scale: float, RNFカーネルの長さスケール    sample_num: 生成するu(·)プロファイルの数        Outputs:    --------    u_sample: 生成されたu(·)プロファイル    """    # 与えられた長さスケールでカーネルを定義    kernel = RBF(length_scale)    # ガウス過程回帰器を作成    gp = GaussianProcessRegressor(kernel=kernel)    # コロケーションポイントの場所    X_sample = np.linspace(0, 1, 100).reshape(-1, 1)         # サンプルを作成    u_sample = np.zeros((sample_num, 100))    for i in range(sample_num):        # 事前に直接サンプリング        n = np.random.randint(0, 10000)        u_sample[i, :] = gp.sample_y(X_sample, random_state=n).flatten()              return u_sample

上記のコードでは：

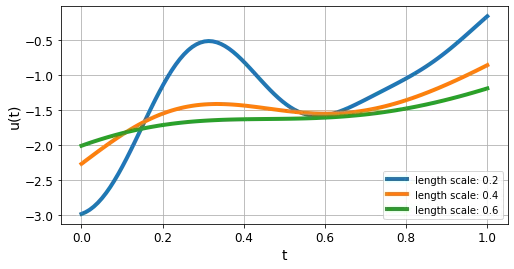
1. length_scale を使用して生成される関数の形状を制御します。RBFカーネルの場合、図11は異なるカーネルの長さスケールに対するu(·)プロフィールを示しています。
2. DeepONet にフィードする前に、u(·) を離散化する必要があることを思い出してください。これは、興味のある時間領域内に一様に分布した100個のポイントを割り当てる X_sample 変数を指定することで行われます。
3. scikit-learnでは、GaussianProcessRegressor オブジェクトは、指定された長さスケールのカーネルを使用してガウス過程からランダムサンプルを抽出するための sample_y メソッドを公開しています。注意点として、GaussianProcessRegressor オブジェクトを使用する前に .fit() を呼び出さなかったことに注意してください。これは、通常の scikit-learn の回帰器とは異なり、GaussianProcessRegressor が提供した 厳密な length_scale を使用するためです。もし .fit() を呼び出すと、length_scale は他の値に最適化され、与えられたデータによりよく適合するようになります。
4. 出力の u_sample は、sample_num * 100 の次元を持つ行列です。各行の u_sample は、100個の離散値からなる u(·) の1つのプロファイルを表します。

4.2 データセットの生成

u(·)プロファイルを生成したので、DeepONetモデルにフィードできるようにデータセットを整理する方法に焦点を当てましょう。

前のセクションで開発したDeepONetモデルでは、次の3つの入力が必要です：

1. 時間座標tは、0から1までのスカラーです（一時的なバッチサイズは考慮しません）。
2. u(·)のプロファイルは、0から1までの事前定義された固定時間座標で評価されたu(·)値から成るベクトルです。
3. u(t)の値は、再びスカラーです。このu(t)の値は、時間座標tでODE損失を計算するために使用されます。

したがって、次のように単一のサンプルを定式化できます：

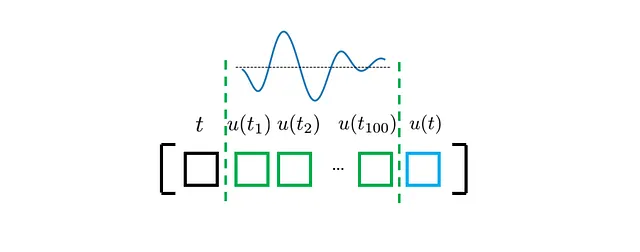
もちろん、各u(·)プロファイル（上図の緑で表示されています）について、ODE損失を評価するために複数のt（および対応するu(t)）を考慮する必要があります。理論的には、tは考慮される時間領域（このケーススタディでは0から1まで）で任意の値を取ることができます。ただし、事前に定義された時間座標でu(·)プロファイルが離散化されている場所でのtのみを考慮します。その結果、更新されたデータセットは次のようになります：

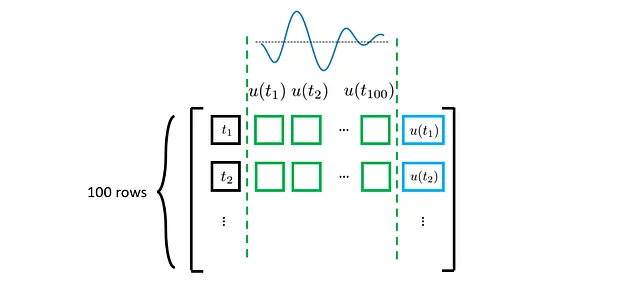
上記の議論では、単一のu(·)プロファイルのみを考慮しています。すべてのu(·)プロファイルを考慮すると、最終的なデータセットは次のようになります：

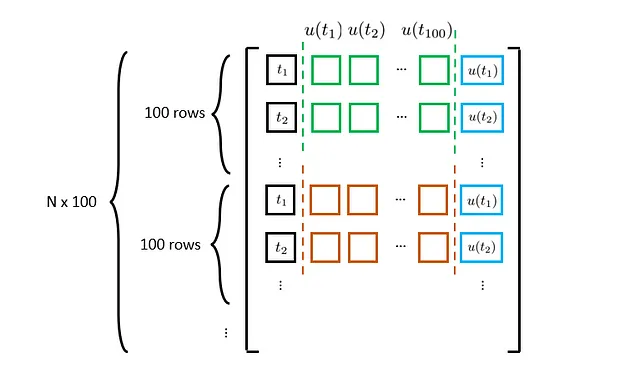
Nはu(·)プロファイルの数を表します。これを考慮に入れて、いくつかのコードを見てみましょう：

from tqdm import tqdmfrom scipy.integrate import solve_ivpdef generate_dataset(N, length_scale, ODE_solve=False):    """物理情報付きDeepONetトレーニングのためのデータセットを生成します。        Args:    ----    N: int, u(·)プロファイルの数    length_scale: float, RNFカーネルの長さスケール    ODE_solve: boolean, 対応するs(·)を計算するかどうかを示します。        Outputs:    --------    X: t、u(·)プロファイル、およびu(t)のデータセット    y: 対応するODEソリューションs(·)のデータセット    """        # ランダムフィールドの作成    random_field = create_samples(length_scale, N)        # データセットのコンパイル    X = np.zeros((N*100, 100+2))    y = np.zeros((N*100, 1))    for i in tqdm(range(N)):        u = np.tile(random_field[i, :], (100, 1))        t = np.linspace(0, 1, 100).reshape(-1, 1)        # tで評価されたu(·)        u_t = np.diag(u).reshape(-1, 1)        # 全体の行列の更新        X[i*100:(i+1)*100, :] = np.concatenate((t, u, u_t), axis=1)        # ODEの解決        if ODE_solve:            sol = solve_ivp(lambda var_t, var_s: np.interp(var_t, t.flatten(), random_field[i, :]),                             t_span=[0, 1], y0=[0], t_eval=t.flatten(), method='RK45')            y[i*100:(i+1)*100, :] = sol.y[0].reshape(-1, 1)            return X, y

上記のコードでは、与えられたu（·）プロファイルに対して対応するs（·）を計算する1つのオプションを追加します。トレーニングではs（·）の値を使用しませんが、モデルのパフォーマンスをテストするためにそれらが必要です。s（·）の計算は、特に初期値問題を解くために設計されたSciPyのODEソルバであるscipy.integrate.solve_ivpを使用して実現されます。

次に、トレーニング、検証、テストデータセットを生成します。このケーススタディでは、u（·）プロファイルを生成し、物理情報を持つDeepONetをトレーニングするために長さスケール0.4を使用します。

# トレーニングデータセットの作成
N_train = 2000
length_scale_train = 0.4
X_train, y_train = generate_dataset(N_train, length_scale_train)

# 検証データセットの作成
N_val = 100
length_scale_test = 0.4
X_val, y_val = generate_dataset(N_val, length_scale_test)

# テストデータセットの作成
N_test = 100
length_scale_test = 0.4
X_test, y_test = generate_dataset(N_test, length_scale_test, ODE_solve=True)

4.3 データセットの組織化

最後に、NumPy配列をTensorFlowデータセットオブジェクトに変換してデータの取り込みを容易にします。

# バッチサイズの決定
ini_batch_size = int(2000/100)
col_batch_size = 2000

# データセットオブジェクトの作成（初期条件）
X_train_ini = tf.convert_to_tensor(X_train[X_train[:, 0]==0], dtype=tf.float32)
ini_ds = tf.data.Dataset.from_tensor_slices((X_train_ini))
ini_ds = ini_ds.shuffle(5000).batch(ini_batch_size)

# データセットオブジェクトの作成（補完点）
X_train = tf.convert_to_tensor(X_train, dtype=tf.float32)
train_ds = tf.data.Dataset.from_tensor_slices((X_train))
train_ds = train_ds.shuffle(100000).batch(col_batch_size)

# スケーリング
mean = {
    'forcing': np.mean(X_train[:, 1:-1], axis=0),
    'time': np.mean(X_train[:, :1], axis=0)
}
var = {
    'forcing': np.var(X_train[:, 1:-1], axis=0),
    'time': np.var(X_train[:, :1], axis=0)
}

上記のコードでは、2つの異なるデータセット（train_dsはODE損失を評価するため、ini_dsは初期条件の損失を評価するため）を作成します。また、tとu（·）の平均値と分散値も事前に計算しています。これらの値は、入力を標準化するために使用されます。

これでデータの生成と組織化が完了しました。次に、モデルのトレーニングを開始し、パフォーマンスを確認します。

5. 物理情報を持つDeepONetのトレーニング

まず、損失の進化を追跡するためのカスタムクラスを作成します：

from collections import defaultdict

class LossTracking:
    def __init__(self):
        self.mean_total_loss = keras.metrics.Mean()
        self.mean_IC_loss = keras.metrics.Mean()
        self.mean_ODE_loss = keras.metrics.Mean()
        self.loss_history = defaultdict(list)
        
    def update(self, total_loss, IC_loss, ODE_loss):
        self.mean_total_loss(total_loss)
        self.mean_IC_loss(IC_loss)
        self.mean_ODE_loss(ODE_loss)
        
    def reset(self):
        self.mean_total_loss.reset_states()
        self.mean_IC_loss.reset_states()
        self.mean_ODE_loss.reset_states()
        
    def print(self):
        print(f"IC={self.mean_IC_loss.result().numpy():.4e}, \              
              ODE={self.mean_ODE_loss.result().numpy():.4e}, \              
              total_loss={self.mean_total_loss.result().numpy():.4e}")
              
    def history(self):
        self.loss_history['total_loss'].append(self.mean_total_loss.result().numpy())
        self.loss_history['IC_loss'].append(self.mean_IC_loss.result().numpy())
        self.loss_history['ODE_loss'].append(self.mean_ODE_loss.result().numpy())

次に、メインのトレーニング/検証ロジックを定義します：

# トレーニングの設定
n_epochs = 300
IC_weight = tf.constant(1.0, dtype=tf.float32)
ODE_weight = tf.constant(1.0, dtype=tf.float32)
loss_tracker = LossTracking()
val_loss_hist = []

# オプティマイザの設定
optimizer = keras.optimizers.Adam(learning_rate=1e-3)

# PINNモデルのインスタンス化
PI_DeepONet = create_model(mean, var)
PI_DeepONet.compile(optimizer=optimizer)

# コールバックの設定
callbacks = [
    keras.callbacks.ReduceLROnPlateau(factor=0.5, patience=30),
    tf.keras.callbacks.ModelCheckpoint('NN_model.h5', monitor='val_loss', save_best_only=True)
]
callbacks = tf.keras.callbacks.CallbackList(_callbacks, add_history=False, model=PI_DeepONet)

# トレーニングプロセスの開始
for epoch in range(1, n_epochs + 1):
    print(f"Epoch {epoch}:")
    for X_init, X in zip(ini_ds, train_ds):
        # 勾配の計算
        ODE_loss, IC_loss, total_loss, gradients = train_step(X, X_init, 
                                                              IC_weight, ODE_weight,
                                                              PI_DeepONet)
        # 勾配降下
        PI_DeepONet.optimizer.apply_gradients(zip(gradients, PI_DeepONet.trainable_variables))
        
        # 損失の追跡
        loss_tracker.update(total_loss, IC_loss, ODE_loss)
        
    # 損失のサマリー
    loss_tracker.history()
    loss_tracker.print()
    loss_tracker.reset()
    
    ####### 検証
    val_res = ODE_residual_calculator(X_val[:, :1], X_val[:, 1:-1], X_val[:, -1:], PI_DeepONet)
    val_ODE = tf.cast(tf.reduce_mean(tf.square(val_res)), tf.float32)
    
    X_val_ini = X_val[X_val[:, 0]==0]
    pred_ini_valid = PI_DeepONet.predict({"forcing": X_val_ini[:, 1:-1], "time": X_val_ini[:, :1]}, batch_size=12800)
    val_IC = tf.reduce_mean(keras.losses.mean_squared_error(0, pred_ini_valid))
    
    print(f"val_IC: {val_IC.numpy():.4e}, val_ODE: {val_ODE.numpy():.4e}, lr: {PI_DeepONet.optimizer.lr.numpy():.2e}")
    
    # エポックの終了時のコールバック
    callbacks.on_epoch_end(epoch, logs={'val_loss': val_IC+val_ODE})
    val_loss_hist.append(val_IC+val_ODE)
    
    # データセットの再シャッフル
    ini_ds = tf.data.Dataset.from_tensor_slices((X_train_ini))
    ini_ds = ini_ds.shuffle(5000).batch(ini_batch_size)
    train_ds = tf.data.Dataset.from_tensor_slices((X_train))
    train_ds = train_ds.shuffle(100000).batch(col_batch_size)

これはかなり長いコードの塊ですが、すでに重要な部分をすべてカバーしているため、自己説明的であるはずです。

トレーニングのパフォーマンスを視覚化するために、損失の収束曲線をプロットできます:

# 履歴fig、ax = plt.subplots(1, 3, figsize=(12, 4))ax[0].plot(range(n_epochs), loss_tracker.loss_history['IC_loss'])ax[1].plot(range(n_epochs), loss_tracker.loss_history['ODE_loss'])ax[2].plot(range(n_epochs), val_loss_hist)ax[0].set_title('IC Loss')ax[1].set_title('ODE Loss')ax[2].set_title('Val Loss')for axs in ax:    axs.set_yscale('log')

トレーニングの結果は次のようになります:

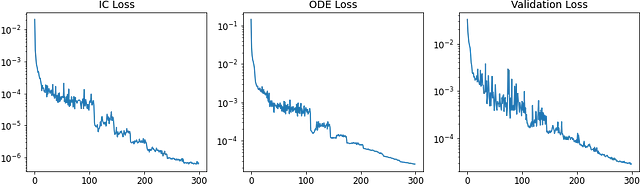
さらに、トレーニング中に特定のターゲットs(·)の予測精度がどのように進化するかも見ることができます:

トレーニングの初めには、モデルの予測と真の値との間に明らかな乖離が見られます。しかし、トレーニングの終わりには、予測されたs(·)が真の値に収束していることがわかります。これは、私たちの物理学に基づいたDeepONetが適切に学習していることを示しています。

6. 結果の議論

トレーニングが完了したら、保存された重みを再ロードしてパフォーマンスを評価することができます。

ここでは、テストデータセットからランダムに3つのu(·)プロファイルを選び、物理学に基づいたDeepONetによって予測された対応するs(·)と数値ODEソルバによって計算されたs(·)を比較します。予測と真の値はほとんど区別がつきません。

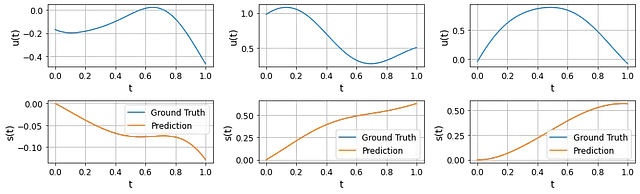
これらの結果は非常に驚くべきものです。なぜなら、DeepONetのトレーニングにおいてs(·)の観測データ（初期条件を除く）を使用していないからです。これは、支配的なODE自体が正確な予測をするための十分な「監督」信号を提供していることを示しています。

評価するもう一つの興味深いことは、いわゆる「分布外」予測能力です。DeepONetのトレーニング時に支配方程式を強制したため、トレーニングu(·)の分布外にあるu(·)プロファイルに対しても、トレーニングされた物理学に基づいたDeepONetがまだまともな予測を行えることが期待されます。

それをテストするために、異なる長さスケールでu(·)プロファイルを生成することができます。次の結果は、長さスケール0.6で生成された3つのu(·)プロファイルと予測されたs(·)を示しています。これらの結果はかなり素晴らしいですが、物理学に基づいたDeepONetは長さスケール0.4でトレーニングされています。

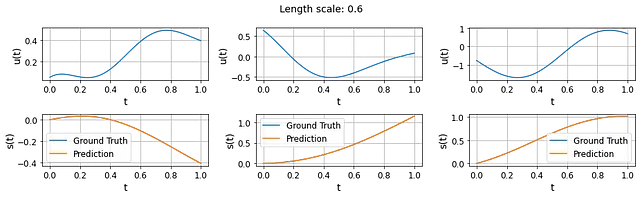
ただし、長さスケールを0.2に縮小し続けると、明らかな乖離が現れ始めることに注意する必要があります。これは、トレーニングされた物理学に基づいたDeepONetの一般化能力には限界があることを示しています。

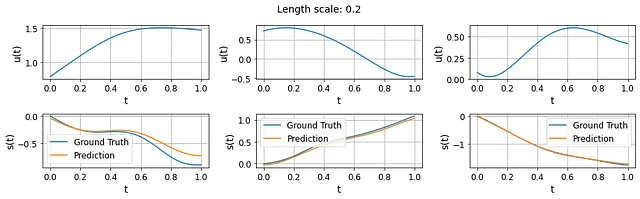
一般的に、より小さい長さスケールは、訓練に使用されるu(·)プロファイルとはかなり異なる、より複雑なu(·)プロファイルにつながります。これは、訓練されたモデルが小さい長さスケールの領域で正確な予測をするのに課題を抱えた理由となる可能性があります。

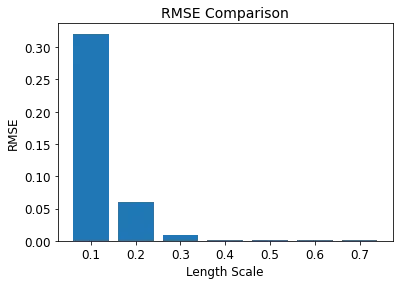
全体的に言えば、開発された物理情報DeepONetは、ODEの制約条件のみを与えられた場合でも、システムのダイナミクスを適切に学習し、入力関数から出力関数へのマッピングを行うことができます。さらに、物理情報DeepONetは「分布外」の予測を処理する能力を一定程度持っており、支配するODEと一致するようにモデルを訓練することがモデルの汎化能力を向上させることを示しています。

7. 要点

物理情報DeepONetの探求は長い道のりを経てきました。DeepONetと物理情報学習の基本的な概念を理解し、コードの実装を通じてその実際の動作を見ることから、微分方程式を解くこの強力な方法について多くをカバーしました。

以下はいくつかの主な要点です：

1️⃣ DeepONetは、枝とトランクのネットワークの新しいアーキテクチャにより、演算子の学習を行うための強力なフレームワークです。

2️⃣ 物理情報学習は、動力学系の支配微分方程式を学習プロセスに明示的に組み込むことで、モデルの解釈可能性と汎化能力の向上の可能性を持っています。

3️⃣ 物理情報DeepONetは、DeepONetと物理情報学習の長所を組み合わせたものであり、関連する支配方程式に従いながら機能的なマッピングを学習するための有望なツールとして位置づけられます。

物理情報DeepONetへの深い探求をお楽しみいただけたでしょうか。次は、物理情報DeepONetを用いた逆問題の解決に向けてギアを切り替えます。お楽しみに🤗

こちらで完全なコードを含む関連ノートブックを見つけることができます 💻

参考文献

[1] Lu et al., DeepONet: Learning nonlinear operators for identifying differential equations based on the universal approximation theorem of operators. arXiv, 2019.

[2] Wang et al., Learning the solution operator of parametric partial differential equations with physics-informed DeepOnets. arXiv, 2021.

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!