データサイエンスによる在庫最適化:Pythonによるハンズオンチュートリアル
'Inventory Optimization through Data Science' 'Pythonによるハンズオンチュートリアル' translates to 'Hands-on Tutorial with Python' The condensed translation is 'Inventory Optimization through Data Science Hands-on Tutorial with Python
パート1: 在庫最適化のためのマルコフプロセスの実装についての優しい紹介。

イントロ
在庫最適化はトリッキーなパズルのようなものです。広範な問題として、様々な領域で発生し、自分の店舗のために何個の商品を注文すべきかを考えることに関わります。
例えば、自転車店のオーナーが販売用に新しい自転車を注文するとします。しかし、ここにはトリッキーな状況があります。店舗に対して自転車を多く注文すると、自転車の保守と保管に費用がかかりすぎます。一方、自転車を少なく注文すると、顧客の需要に対応できなくなり、利益と評判の損失になります。
彼女が必要なのは、在庫の長期的な利益を確保するために、毎日の最適な注文量についての最適な「戦略」です。
したがって、この問題の文脈において、プログラミング、データ、モデリングの知識を持つデータサイエンティストは、この最適な「戦略」を見つける上で重要な役割を果たすことができます。しかし、その目標(その問いに答えるための)を達成するためには、いくつかの基礎的な知識が必要です。具体的には以下の基本的な理解が必要です:
- マルコフプロセス
- マルコフ報酬プロセス
- およびマルコフ決定過程
- 最後に、これらの3つの概念を組み合わせ、
- 動的計画法と
- 強化学習と結びつけます
上記の最適な「戦略」に到達するために。このブログでは、Pythonで「マルコフプロセス」を理解し、モデル化することを目指します。これは次のステップの基礎となります。
在庫最適化:既製の機械学習モデルで解決できるのでしょうか?
正直に言うと、私はこのブログを「フラストレーションから」書きました。オンラインのリソースで在庫最適化がどのようにモデル化され、解決されているかを見たかったのです。私は博士号で在庫最適化に取り組んだことがあり、(私のトピックが順次意思決定に関するものであるため)いくつかの研究や論文を読み、適切なモデリング手法を見つけることができました。
ポイントは、「在庫最適化」タイプの問題は動的な問題であり、現在の状態(在庫状況)に応じて適応し、適応的なポリシーを持つ必要があるということです。
在庫最適化は、静的な解析手法で対処できる静的な問題ではなく、既製の機械学習/深層学習モデルを使用して解決できるものではありません。毎日の意思決定を動的に適応させるために、その構成要素を理解し、モデル化する必要がある動的なプロセスです。
マルコフプロセス
アナリティクスのプロフェッショナル(データサイエンティスト、アナリストなど)であれば、時間にインデックスされ、不確かな経路に従うプロセスを扱うことがよくあります。例えば、エネルギー会社で働くデータサイエンティストを考えてみましょう。彼女の仕事は、商品価格の不確かな経路を追跡することです。
商品価格(例えば石油)は時間ステップt=0,1,2,⋯で経路をたどります。これは時間によってインデックスされた不確かなプロセスです。しかし、分析を行うためには、プロセスを内部的に表現する必要があります。
状態
状態は、不確かなプロセスを内部的に表現するためのツールと考えてください。先ほどの石油価格の例に戻りましょう。今日の石油価格が100ドルだとします。その情報をS_0=100と表現することができます。そして、明日の価格は異なる値になり、S_1として表現できます。このようなシーケンスが続きます S_0, S_1, S_2. このプロセスは、ランダムな状態St∈Sのシーケンスです。時間t=0,1,2,3,.. におけるプロセスは以下のように表現できます:

マルコフ特性
ここでは、この短いブログでマルコフプロセスについて話したいと思います。プロセスがマルコフ特性を持つ場合、状態の遷移は次のような特性を持っていると言います。

この方程式は、簡単な言葉でどういう意味を持つのでしょうか?
天候の簡単な例を考えてみましょう。一日には「晴れ」「雨」「雪」の3つの天候条件が考えられるとします。そうすると、今日が「晴れ」の場合、
- 明日も「晴れ」になる確率は70%です。
- 明日は「雨」になる確率は20%です。
- 明日の天候が「雪」になる確率は10%です。
この天候の例では、明日の天候条件の確率は「今日」だけに依存しているため、天候の履歴は「関係ない」と言えます。今日の天候が晴れ(St=「晴れ」)である限り、明日の天候がP(S_{t+1}=「晴れ」)=0.7、P(S_{t+1}=「雨」)=0.2、P(S_{t+1}=「雪」)=0.1の確率で起こると言えます。
マルコフプロセスをより理解するために、簡単な現実世界の例を見てみましょう。ここでは、自転車店の在庫管理についての例を取り上げ、Pythonのコーディングにも触れていきます。
自転車店の在庫管理の簡単な例
自転車店の例に戻ります。自転車の在庫を保持できる容量が限られている(最大5台)と想定してください。
毎日、いくつかの顧客が店舗から自転車を購入しに来ます。今日(水曜日)は店舗に自転車が3台あります。しかし、明日(木曜日)は店舗に需要があることを知っています。つまり、いくつかの自転車が売れることを意味します。明日の顧客の数はわからないため、明日の自転車の需要は不確定です。このプロセスをより正確にモデル化し、在庫の状態がどのように変化し、進化するかをモデル化する必要があります。¹
問題の説明
このブログでは、主にマルコフプロセスに焦点を当てています。つまり、このブログでは(仮定して)固定のポリシー(この場合は毎日何台の自転車を注文するか)があるとします。この例のマルコフプロセスをモデル化するためには、まずこの問題をフレーム化する必要があります(状態は何ですか?)。次に、状態の遷移モデルを構築する必要があります。
状態(プロセスの内部表現)は、次の2つの要素で表すことができます:
- α:店舗にすでにある自転車の数
- β:前日に注文し、明日の朝到着する予定の自転車の数(これらの自転車はトラックに積まれています)
24時間サイクルのシーケンス
この自転車店の24時間サイクルのイベントのシーケンスは次のとおりです:
- 午後6時:状態S_t:(α,β)を観測します
- 午後6時:新しい自転車を注文し、max(C−(α+β),0)となります
- 午前6時:36時間前に注文した自転車が到着します
- 午前8時:店舗を開店します
- 午前8時から午後6時まで:一日中の需要iを経験します(ポアソン分布を使用してモデル化されます)
- 午後6時:店舗を閉店します
以下の図は、このシーケンスを視覚化しています:

上記の説明と同様に、St=(αt+βt)はこの確率過程の内部表現であり、マルコフプロセスでは、この確率過程がどのように進化するかをモデル化したいと考えています。
在庫の24時間シーケンスを示す例
例を挙げましょう。デビッドは自転車店のオーナーです。水曜日の午後6時には店舗に自転車が2台あり、月曜日の午後6時に注文した自転車が1台あります。彼の状態は次のようになります:

したがって、水曜日の午後8時の状態はS=(α=2,β=1)です。その後、毎日、非負の整数のランダムな需要が発生し、需要はポアソン分布に従ってモデル化されます(ポアソンパラメータλ∈R>)。i台の自転車の需要(i=0,1,2⋯)は次の確率で発生します:

この分布を可視化して、λ=2を選んだ場合の異なる需要の確率を見ることができます。
# import matplotlib and some desired stylingimport matplotlib.pyplot as plt%matplotlib inlineplt.style.use("ggplot")plt.rcParams["figure.figsize"] = [10, 6]# need numpy to do some numeric calculationimport numpy as np# poisson is used to find pdf of Poisson distribution from scipy.stats import poisson
x_values = np.arange(0,10)# pdf Poisson distri with lambda = 1pdf_x_values = poisson.pmf(k=x_values,mu=2)plt.bar(x_values, pdf_x_values, edgecolor='black')plt.xticks(np.arange(0, 10, step=1))plt.xlabel("顧客の需要")plt.ylabel("顧客の需要の確率")plt.title("λ=1の顧客の需要の確率分布")plt.savefig("fig/poisson_lambda_2.png", dpi=300)plt.show()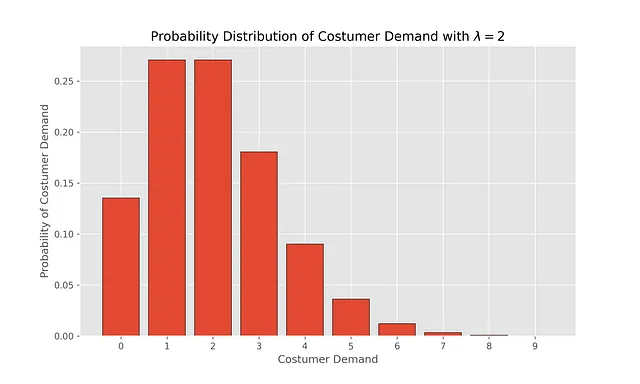
マルコフ過程の確率遷移の構築
ここで、状態St=(α,β)の初期理解があるので、この問題の不確実性を導入する顧客の需要(i)についての確率遷移を構築することができます。それについてのコーディングを行いますが、まずは簡単な言葉で説明しましょう。
この問題の確率遷移には、ケース1とケース2の2つの場合があります。
- ケース1)
需要iがその日の在庫合計よりも小さい場合、初期在庫=α+β
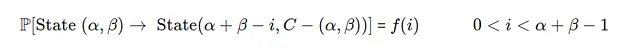
- ケース2)
需要iがその日の在庫合計よりも大きい場合、初期在庫=α+β
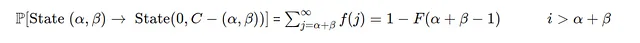
ポアソン分布のCDFである F(α+β−1) です。
この問題の背景を理解した後、Pythonコードを書いてさらに理解していきましょう。このPythonコードの重要な側面は、マルコフ過程の遷移を保存するためのデータ構造を設計することです。そのために、私はデータ構造を辞書として設計し、「MarkovProcessDict」と呼んでいます。この辞書のキーは現在の状態に対応し、値(辞書で表される)は次の状態とそれぞれの次の状態に関連する確率です。これはデータ構造MarkovProcessDictの例です:
from typing import DictMarkovProcessDict = {"Current State A":{"Next State 1, from A": "Probability of Next State 1, from A", "Next State 2, from A": "Probability of Next State 2, from A"}, "Current State B":{"Next State 1, from B": "Probability of Next State 1, from B", "Next State 2, from B": "Probability of Next State 2, from B" }}MarkovProcessDict
データ構造MarkovProcessDictの意味を解説しましょう。例えば、初期状態は「Current State A」であり、次の2つの状態に移行することができます:
- 1) 「Next State 1, from A」、確率は「Probability of Next State 1, from A」
- 2) 「Next State 2, from A」、確率は「Probability of Next State 2, from A」
ハンズオンコーディング
前述のプロセスの2つの異なるケースを考えて、MarkovProcessDictデータ構造を構築するためのコードを書きましょう。
MarkovProcessDict: Dict[tuple, Dict[tuple, float]] = {}user_capacity = 2user_poisson_lambda = 2.0
# 実行する可能性のあるすべての状態を考慮するためのループ# この自転車店を運営する上で直面する可能性のある状態for alpha in range(user_capacity+1): for beta in range(user_capacity + 1 - alpha): # これがSt、現在の状態です state = (alpha, beta) # これが初期在庫、AM8時点で持っている自転車の総数 initial_inventory = alpha + beta # beta1は次の状態のbetaであり、 #現在の状態に関係なく(意思決定方針が一定であるため) beta1 = user_capacity - initial_inventory # 可能な需要のリスト for i in range(initial_inventory +1): # 初期需要が需要を満たせる場合 if i <= (initial_inventory-1): # 特定の需要が発生する確率 transition_prob = poisson.pmf(i,user_poisson_lambda) # データにすでに状態が定義されている場合 if state in MarkovProcessDict: MarkovProcessDict[state][(initial_inventory - i, beta1)]= transition_prob else: MarkovProcessDict[state] = {(initial_inventory - i, beta1):transition_prob } # 初期需要が需要を満たせない場合 else: # 需要が満たされない確率 transition_prob = 1- poisson.cdf(initial_inventory -1, user_poisson_lambda) if state in MarkovProcessDict: MarkovProcessDict[state][(0, beta1)]= transition_prob else: MarkovProcessDict[state] = {(0, beta1 ):transition_prob }上記のコードでは、forループがすべての可能な状態の組み合わせを繰り返し、各状態(St)が次の状態(S_{t+1})に「transition_prob」の確率で移動します。以下のコードでシステムのダイナミクスを表示することができます:
or (state, value) in MarkovProcessDict.items(): print("現在の状態は: {}".format(state)) for (next_state, trans_prob) in value.items(): print("次の状態は {} で確率は {:.2f} です".format(next_state, trans_prob))
最終データ構造の可視化
これらのダイナミクスを理解する方法の1つは、graphvizのPythonパッケージを使用することです。ここでは、各ノードが現在の状態を表し、エッジはその状態から別の状態に移動する確率を示します。
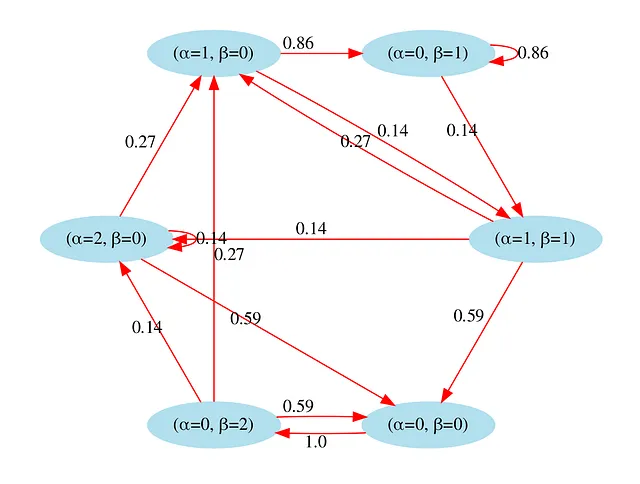
# パッケージのインポートimport graphviz # graphvizの初期構造を定義し、色を薄い青、塗りつぶしスタイルにするd = graphviz.Digraph(node_attr={'color': 'lightblue2', 'style': 'filled'}, )d.attr(size='10,10')d.attr(layout = "circo")for s, v in MarkovProcessDict.items(): for s1, p in v.items(): # s[0]とs[1]でalphaとbetaを表す d.edge("(\u03B1={}, \u03B2={})".format(s[0],s[1]), # pを現在の状態から新しい状態への移動確率として表す "(\u03B1={}, \u03B2={})".format(s1[0],s1[1]), label=str(round(p,2)), color="red") print(d)
以下のプロットでは、この遷移のグラフィックスを視覚化しました。例えば、状態St = (α=1,β=0)(左上の円)である場合、次の状態がS(t+1):(α=0,β=1)になる確率は86%であり、次の状態がS(t+1):(α=1,β=1)になる確率は14%です。
最終的なメモ
- 在庫最適化は静的な最適化問題ではなく、各時間ステージでの不確実性を考慮して最良の決定を行うために適応的なポリシーが必要となる連続的な意思決定です。
- このブログでは、在庫プロセス(状態とマルコフプロセスを使用)を追跡し、Pythonのコーディングを通じてプロセスのダイナミクスを視覚化する数学モデルを構築しました。
- このブログは、在庫最適化問題の対処方法の基礎を築き、次のステップではマルコフ報酬とマルコフ決定プロセスに取り組む予定です。
[1] この例について詳しくは「Financeにおける強化学習の基礎」をご覧ください。ただし、このブログでは理解しやすくするためにPythonコードを書き直しました。
ここまで読んでいただきありがとうございます!
この記事がPythonを使用した在庫最適化について理解しやすいチュートリアルとなっていることを願っています。
在庫最適化とマルコフプロセスについて学ぶのにこの記事が役立ったと思われる場合は、👏をクリックしてフォローしてください!
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
