強化学習 価値反復の簡単な入門

Introduction to Value Iteration in Reinforcement Learning

強化学習の基礎を学び、単純な例題に価値反復を適用する方法を学びましょう

価値反復（Value Iteration、VI）は、典型的には強化学習（Reinforcement Learning、RL）の学習経路で最初に紹介されるアルゴリズムの一つです。このアルゴリズムの基礎的な特性は、RLの最も基本的な側面のいくつかを導入しており、より複雑なRLアルゴリズムに進む前にVIをマスターすることが重要です。しかし、理解するのは難しいかもしれません。

この記事は、VIへの理解を容易にすることを目的としており、RLの分野に新しい読者を想定しています。さあ、始めましょう。

すでにRLの基礎を知っていますか？ → 価値反復の使用方法へスキップ。

• Fast.AIディープラーニングコースからの7つの教訓
• Google AIは、TPUを使用して流体の流れを計算するための新しいTensorFlowシミュレーションフレームワークを導入しました
• アデプトAIラボは、Persimmon-8Bという強力なフルパーミッシブライセンスの言語モデルをオープンソース化しました

RLの基礎

まずは教科書の定義から始めましょう。その後、簡単な例を使って解説します。

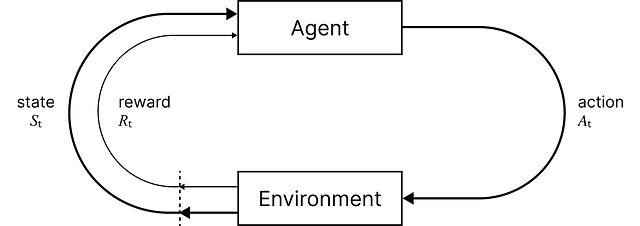
RLは、教師あり学習と教師なし学習と並んで、3つの主要な機械学習のパラダイムの一つです。RLは単一のアルゴリズムではなく、エージェントが環境と相互作用しながら学習し、意思決定を行うためのさまざまな技術と手法を包括するフレームワークです。

RLでは、エージェントがさまざまなアクションを取ることによって環境と相互作用します。エージェントは、それらのアクションが望ましい状態につながる場合に報酬を受け取り、そうでない場合に罰せられます。エージェントの目標は、報酬を最大化するための戦略であるポリシーを学習することです。この試行錯誤のプロセスにより、エージェントの行動ポリシーが洗練され、新しい、未知の環境において最適または近似最適な行動を取ることができるようになります。

Richard S. SuttonとAndrew G. Bartoによる書籍「An Introduction to Reinforcement Learning」は、RLの理解を深めるために最も優れた書籍とされています.. しかも無料で入手できます！

例題を定義しましょう

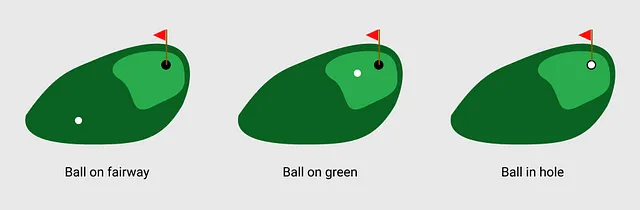
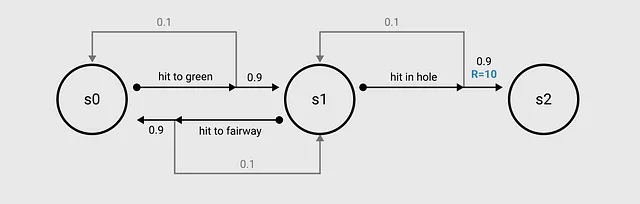
この画像は、ゴルフを最も単純な形で表しています。私たちは、ゴルフの目標が明確に定義されているため、これを使用します – ボールを穴に入れることです。

私たちの例では、ゴルフボールは3つの位置のいずれかに存在します：フェアウェイ上、グリーン上、またはホール内です。私たちはフェアウェイから始めて、各ショットでホールに近づくことを目指します。

RLでは、これらの位置は環境の状態として参照されます。状態は、現在の環境（ゴルフコース）のスナップショットであり、ボールの位置も記録されていると考えることができます。

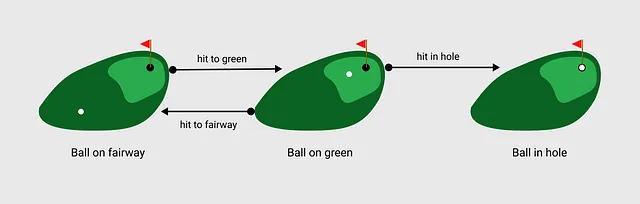
私たちのゲームでは、エージェントはフェアウェイ上のボールからショットを打ちます。 エージェントは単にアクションを行う主体を指します。私たちのゲームには3つの利用可能なアクションがあります：フェアウェイに打つ、グリーンに打つ、ホールに打つ。

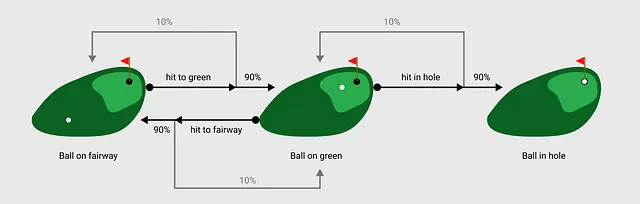
もちろん、ショットを打つとボールが思い通りに行かないこともあります。そのため、アクションと状態をいくつかの確率重み付けで関連付ける遷移関数を導入します。

例えば、フェアウェイからショットを打ち、まだフェアウェイにいる場合に、グリーンを逃すことがあります。RLの文脈で言えば、ボールがフェアウェイ上にある状態で「グリーンに打つ」というアクションを取った場合、ボールがグリーン上に入る確率は90%であり、ボールが再びフェアウェイ上に入る確率は10%です。

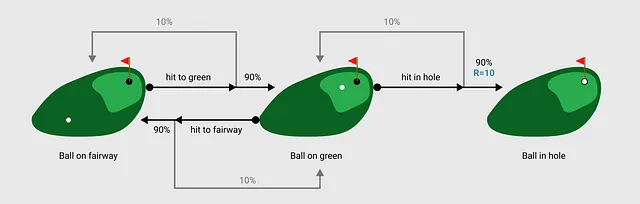
エージェントがアクションを実行するたびに、それを「ステップ」として環境を経由します。実行したアクションに基づいて、エージェントは新しい状態と「報酬」を観測します。報酬関数は、エージェントを正しい方向に推進するためのインセンティブメカニズムです。言い換えると、報酬関数はエージェントの望ましい行動を形成するために設計されます。簡単化されたゴルフの例では、ボールが穴に入った場合に報酬10を提供します。

環境ダイナミクス（遷移関数と報酬関数）の設計は簡単な課題ではありません。環境が解決しようとしている問題を正確に表していない場合、エージェントは正しい問題の正しい解に基づいた方策を学習します。ここではそのような設計要素については触れませんが、それについては言及する価値があります。

マルコフ決定過程

エージェントが理解するために問題を表現するには、それをマルコフ決定過程（MDP）として形式化する必要があります。

MDPは、問題を構造化された方法で記述する数学モデルです。エージェントの環境との相互作用を、連続的な意思決定プロセス（つまり、一つのアクションの後に別のアクションが続く）として表現します。

MDPには以下の要素が含まれます（ここでは数学的な表記を短くするためにいくつかの記述を追加します）：

• 有限の状態の集合 s ∈ S。
• 有限のアクションの集合 a ∈ A。
• 現在の状態 s、現在のアクション a のもとで次の状態 s′ に到達する確率を返す遷移関数 T(s′∣s,a)。
• 現在の状態 s、アクション a を取った後の次の状態 s′ に到達した場合のスカラー報酬を返す報酬関数 R(s,a,s′)。

もし状態間の遷移に不確実性やランダム性がある場合（つまり、同じ状態で同じアクションを二度実行しても異なる結果になる可能性がある場合）、これを「確率的」MDPと呼びます。また、遷移や報酬が完全に予測可能な「決定論的」MDPを作成することもできます。つまり、エージェントが特定の状態でアクションを実行した場合、アクションと結果の次の状態と報酬の間に一対一の対応関係があることを意味します。

MDPとして可視化されたゴルフの問題は、先に描かれた画像とほぼ同じです。省略のために S = {s1, s2, s3} を使用します。

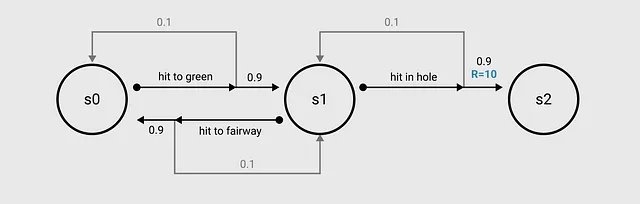
MDPの使用は、環境で次に何が起こるかが現在の状態とアクションに依存し、以前に起こったことには依存しないと仮定しています。これを「マルコフ特性」と呼び、RLでは計算の複雑さを減らすために重要です。後で詳しく説明します。

バリュー反復とは何か？

バリュー反復（VI）は、ゴルフの例のように、MDPのすべてのコンポーネントについて完全な知識を持っているRLの問題を解決するために使用されるアルゴリズムです。各状態にいる「バリュー」の推定値を反復的に改善することによって機能します。これは、異なる利用可能なアクションを取るときに、直近の報酬と将来の報酬を考慮します。これらの値はバリューテーブルを使用して追跡され、各ステップで更新されます。最終的に、この改善の連続の過程が収束し、与えられた環境で最良の意思決定を行うための状態→アクションの最適な方針を生成します。

VIは、大きな問題を小さなサブ問題に分割する動的計画法の概念を活用しています。VIでは、ベルマン方程式を使用して、各状態の値の推定値を反復的に更新するプロセスをガイドし、隣接する状態の値に関連する再帰的な関係を提供します。

これは今のところあまり意味をなしません。VIを学ぶ最も簡単な方法は、ステップバイステップで分解することです。

価値反復アルゴリズムはどのように機能しますか？

以下の画像はアルゴリズムのステップを示しています。見かけよりも簡単ですので、ご安心ください。

まず、トレーニングのためにいくつかのパラメータを定義する必要があります。

• Theta θは収束のための閾値を表します。θに達したら、トレーニングループを終了しポリシーを生成できます。これは、作成するポリシーが十分に正確であることを確認するための方法です。トレーニングを早すぎるタイミングで停止すると、最適なアクションを学ぶことができない場合があります。
• Gamma γは割引率を表します。これは、エージェントが将来の報酬を即時の報酬と比較してどれだけ重視するかを決定する値です。割引率が高い（1に近い）ほど、エージェントは長期的な報酬をより重視します。一方、割引率が低い（0に近い）ほど、即時の報酬をより重視します。

割引率をよりよく理解するために、RLエージェントがチェスをプレイしていると考えてみましょう。次の手で相手のクイーンを取る機会があるとしましょう。これにより即時の大きな報酬が得られます。しかし、同時に、より小さな価値のある駒を犠牲にすることで、将来的な優位性を作り出し、将来的にはチェックメイトとさらなる報酬を得る可能性があります。割引率は、この決定をバランスするのに役立ちます。

(1) 初期化: パラメータが定義されたので、すべての状態の値関数 V(s) を初期化します。通常、すべての状態に対して値を0（または他の任意の定数）に設定します。値関数は、各状態の値を追跡するテーブルと考えることができます。

(2) 外側のループ: これですべてが準備できましたので、値を更新する反復プロセスを開始できます。収束基準（Δ < θ）が満たされるまで外側のループを繰り返します。

外側のループの各パスでは、Δ = 0とします。Delta Δ は、すべての状態での値推定の変化を表すために使用され、この変化Δが指定された閾値θ以下になるまでアルゴリズムは反復を続けます。

(3) 内側のループ: 各状態sに対して、以下の操作を行います。

• 変数vにその状態の現在の値V(s)を設定します。これは値テーブルから取得されます（最初のパスではv = V(s) = 0となります）。
• ベルマン方程式を使用してV(s)を更新します。
• Δを更新します（後で戻ってきます）。

ベルマン方程式

このアルゴリズムのこの行は最も重要です。この行では、ループで参照している現在の状態の値を更新する必要があります。この値は、その特定の状態から利用可能なすべてのアクションを考慮して計算されます（1ステップ先の予測）。各アクションを実行すると、一連の可能な次の状態s′とそれに対応する報酬rが得られます。

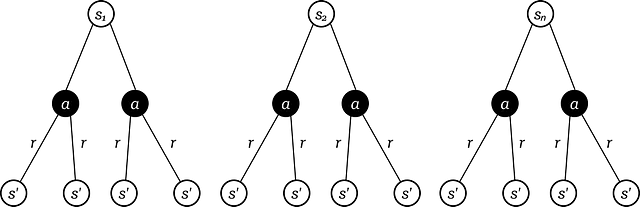
したがって、それぞれの次の状態s′と対応する報酬rに対して、p(s′, r|s, a)[r + γV(s′)]を実行します。これを分解してみましょう：

• p(s′, r|s, a)は、状態sで行動aを取り、次の状態s′に到達する確率です（これは遷移関数です）
• [r + γV(s′)]は、次の状態s′に到達する際の報酬r（報酬関数から取得）+ 次の状態s′の価値V(s′)に対する割引率γを掛けたもの（価値テーブルから取得）です
• これらの2つの部分p(s′, r|s, a) * [r + γV(s′)]を掛け算します

これは1つの次の状態s′（ツリーの3番目のレベル）の計算ですが、aを取った後のすべての可能な次の状態s′に対してこれを繰り返す必要があります。

これを行った後、先ほど得られたすべての結果を合計しますΣₛ′, ᵣ p(s′, r|s, a) * [r + γV(s′)]。そして、この操作をツリーの2番目のレベルである各行動aに対して繰り返します。

これらの手順が完了すると、内部ループで見ている現在の状態sに関連付けられた各行動aに値が割り当てられます。最大値を使用してこれを選択し、その状態に対する新しい値として設定しますV(s)←maxₐ Σₛ′, ᵣ p(s′, r|s, a) * [r + γV(s′)]。

これは、このプロセスが1つの状態s（ツリーの最初のレベル）に対してのみ適用されることを忘れないでください。

もしもこれをプログラムで実装する場合、ツリーの各レベルごとに3つのforループが必要です：

(3) 内部ループ（続き）：内部ループの次のパスに移る前に、現在のΔの値とこの状態の前の値vと新しく計算したこの状態の値V(s)の差を比較します。これら2つのうち大きい方の値をΔ ← max(Δ,| v – V(s)|)として更新します。これは収束までの距離を追跡するのに役立ちます。

これで内部ループの1回が完了します。(3)の手順をS内のすべてのsに対して実行し、内部ループを抜けて収束条件のチェックΔ < θを行います。この条件が満たされた場合、外部ループを抜けます。そうでなければ、(2)の手順に戻ります。

(4) 方策の抽出：この時点で、おそらく外部ループを複数回実行して収束するまでです。つまり、価値テーブルは各状態の最終的な値（つまり、「各状態での良さ」）を表すように更新されます。これに基づいて方策を抽出できます。

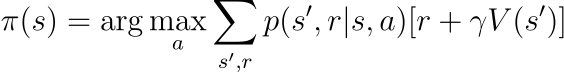
方策πは基本的には状態 → 行動のマッピングであり、各状態に対して期待される報酬を最大化する行動を選択します。これを計算するために、前と同じプロセスを実行しますが、maxₐではなく、argmaxₐを使用して最良の値を与える行動aを取得します。

それでおしまいです！

ポリシーイテレーションは、別の動的計画法のアルゴリズムです。VIと似ていますが、現在の価値関数に基づいてポリシーを貪欲に改善し、ポリシーのパフォーマンスを収束するまで評価する点で異なります。より少ない反復回数を必要とする一方、より多くの計算を必要とします。

価値反復を使って例題を解く

ゴルフのMDPを解くために、例題を使ってVIがさらに理解しやすくなるはずですので、ゴルフのMDPの解を求めましょう。

まず、標準的な値を使用してモデルパラメータを定義します：

γ = 0.9 // 割引率θ = 0.01 // 収束の閾値

次に、Sの状態に対して値テーブルを0で初期化します：

// 値テーブルV(s0) = 0V(s1) = 0V(s2) = 0

そして外側のループを開始します：

Δ = 0

そして、Sの各状態に対して内側のループを3回実行します：

// Bellman更新則// V(s) ← maxₐ Σₛ′, ᵣ p(s′, r|s, a) * [r + γV(s′)]//******************* 状態 s0 *******************//v = 0// ここでは1つのアクションのみを見ていますが、他のアクションは不可能であり、したがって0になりますV(s0) = max[T(s0 | s0, グリーンへの打球) * (R(s0, グリーンへの打球, s0) + γ * V(s0)) +            T(s1 | s0, グリーンへの打球) * (R(s0, グリーンへの打球, s1) + γ * V(s1))]V(s0) = max[0.1 * (0 + 0.9 * 0) +             0.9 * (0 + 0.9 * 0)]V(s0) = max[0] = 0// Delta更新則// Δ ← max(Δ,| v - V(s)|)Δ = max[Δ, |v - v(s0)|] = max[0, |0 - 0|] = 0//******************* 状態 s1 *******************//v = 0// ここでは2つのアクションが可能ですV(s1) = max[T(s0 | s1, フェアウェイへの打球) * (R(s1, フェアウェイへの打球, s0) + γ * V(s0)) +             T(s1 | s1, フェアウェイへの打球) * (R(s1, フェアウェイへの打球, s1) + γ * V(s1)),            T(s1 | s1, 穴への打球) * (R(s1, 穴への打球, s1) + γ * V(s1)) +             T(s2 | s1, 穴への打球) * (R(s1, 穴への打球, s2) + γ * V(s2))]V(s1) = max[0.9 * (0 + 0.9 * 0) +             0.1 * (0 + 0.9 * 0),            0.1 * (0 + 0.9 * 0) +             0.9 * (10 + 0.9 * 0)]V(s1) = max[0, 9] = 9Δ = max[Δ, |v - v(s1)|] = max[0, |0 - 9|] = 9//******************* 状態 s2 *******************//// 終端状態でアクションは不可能です

これにより、値テーブルが以下のように更新されます：

V(s0) = 0V(s1) = 9V(s2) = 0

終端状態s2については心配する必要はありません。ここではアクションが不可能です。

そして、内側のループを抜けて外側のループを続け、以下の収束チェックを実行します：

Δ < θ = 9 < 0.01 = False

収束していないので、外側のループの二回目のイテレーションを行います:

Δ = 0

そして、更新された値テーブルを使用して内側のループをさらに3回繰り返します:

//******************* state s0 *******************//v = 0V(s0) = max[T(s0 | s0, hit to green) * (R(s0, hit to green, s0) + γ * V(s0)) +            T(s1 | s0, hit to green) * (R(s0, hit to green, s1) + γ * V(s1))]V(s0) = max[0.1 * (0 + 0.9 * 0) +             0.9 * (0 + 0.9 * 9)]V(s0) = max[7.29] = 7.29Δ = max[Δ, |v - v(s0)|] = max[0, |0 - 7.29|] = 7.29//******************* state s1 *******************//v = 9V(s1) = max[T(s0 | s1, hit to fairway) * (R(s1, hit to fairway, s0) + γ * V(s0)) +             T(s1 | s1, hit to fairway) * (R(s1, hit to fairway, s1) + γ * V(s1)),            T(s1 | s1, hit in hole) * (R(s1, hit in hole, s1) + γ * V(s1)) +             T(s2 | s1, hit in hole) * (R(s1, hit in hole, s2) + γ * V(s2))]V(s1) = max[0.9 * (0 + 0.9 * 7.29) +             0.1 * (0 + 0.9 * 9),            0.1 * (0 + 0.9 * 9) +             0.9 * (10 + 0.9 * 0)]V(s1) = max(6.7149, 9.81) = 9.81Δ = max[Δ, |v - v(s1)|] = max[7.29, |9 - 9.81|] = 7.29//******************* state s2 *******************//// 終了状態で、行動はなし

二回目のイテレーションの終わりに、値は以下の通りです:

V(s0) = 7.29V(s1) = 9.81V(s2) = 0

再度収束をチェックします:

Δ < θ = 7.29 < 0.01 = False

まだ収束していないので、Δ < θ となるまで上記のプロセスを続けます。すべての計算を表示する必要はありませんが、上記の2つはプロセスを理解するのに十分です。

6回のイテレーション後、方策が収束します。各イテレーションごとに値と収束率が変化するので、以下に示します:

Iteration   V(s0)        V(s1)        V(s2)        Δ             Converged1           0            9            0            9             False2           7.29         9.81         0            7.29          False3           8.6022       9.8829       0            1.3122        False4           8.779447     9.889461     0            0.177247      False5           8.80061364   9.89005149   0            0.02116664    False6           8.8029969345 9.8901046341 0            0.0023832945  True

今、方策を抽出できます:

// 方策抽出のルール// π(s) = argmaxₐ Σₛ′, ᵣ p(s′, r|s, a) * [r + γV(s′)]//******************* state s0 *******************//// s0から可能なアクションは1つだけわかっていますが、とりあえず行いますπ(s0) = argmax[T(s0 | s0, hit to green) * (R(s0, hit to green, s0) + γ * V(s0)) +            T(s1 | s0, hit to green) * (R(s0, hit to green, s1) + γ * V(s1))π(s0) = argmax[0.1 * (0 + 0.9 * 8.8029969345) +             0.9 * (0 + 0.9 * 9.8901046341)]π(s0) = argmax[8.80325447773]π(s0) = hit to green//******************* state s1 *******************//π(s1) = argmax[T(s0 | s1, hit to fairway) * (R(s1, hit to fairway, s0) + γ * V(s0)) +             T(s1 | s1, hit to fairway) * (R(s1, hit to fairway, s1) + γ * V(s1)),            T(s1 | s1, hit in hole) * (R(s1, hit in hole, s1) + γ * V(s1)) +             T(s2 | s1, hit in hole) * (R(s1, hit in hole, s2) + γ * V(s2))]V(s1) = max[0.9 * (0 + 0.9 * 8.8029969345) +             0.1 * (0 + 0.9 * 9.8901046341),            0.1 * (0 + 0.9 * 9.8901046341) +             0.9 * (10 + 0.9 * 0)]π(s1) = argmax[8.02053693401, 9.89010941707]π(s1) = hit in hole

最終的なポリシーは次のようになります：

π(s0) = グリーンに打つπ(s1) = 穴に打つπ(s2) = 終端状態（アクションなし）

したがって、エージェントがフェアウェイ上のボールの状態（s0）にある場合、最良のアクションはグリーンに打つです。これは唯一の利用可能なアクションであるため、非常に明白です。しかし、s1の場合、2つの可能なアクションがあるため、ポリシーは穴に打つと学習しました。これにより、学習済みのポリシーをゴルフをしたい他のエージェントに提供できます！

以上です！バリュー反復を使用して非常にシンプルなRL問題を解決しました。

動的計画法の制約事項

バリュー反復は、他の動的計画法アルゴリズムと同様に、制約事項があります。まず、バリュー反復は、MDPのダイナミクスに完全な知識があることを前提としています（これをモデルベースの強化学習と呼びます）。しかし、実世界の問題では、遷移確率がわからない場合がほとんどです。このような問題では、Q学習（モデルフリーの強化学習）などの他の手法を使用する必要があります。

さらに、より大きな問題では、状態とアクションの数が増えるにつれて、価値テーブルのサイズが指数関数的に増加します（将棋のすべての可能な状態を定義しようとすることを考えてみてください）。これにより、計算およびメモリの要件が急速にエスカレートし、高次元の問題にDPを適用することが困難になる「次元の呪い」の問題が生じます。

それにもかかわらず、VIはRLの基礎的な概念を学ぶ上で非常に役立ちます。これらの概念は、より複雑なアルゴリズムの基盤となる可能性があります。

お読みいただきありがとうございます！

この記事が強化学習と特にバリュー反復の理解に役立ったことを願っています。

もし新しいことを学んだ場合は、👏してフォローしてください！

特に記載がない限り、すべての画像は著者によって作成されたものです。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!