「オーディオ機械学習入門」

Introduction to Audio Machine Learning

私は現在、音声音声認識システムを開発しているため、それに関する基本的な知識を磨く必要がありました。この記事はその結果です。

オーディオの紹介

目次

1. 紹介

音 —

• 音は連続信号であり、無限の信号値を持っています
• デジタルデバイスは有限の配列を必要とするため、それらを離散値の系列に変換する必要があります
• 別名デジタル表現
• 音のパワー — エネルギーが転送される速度（ワット）
• 音の強度 — 面積当たりの音のパワー（ワット/㎡）

オーディオファイルフォーマット —

1. .wav
2. .flac（フリーロスレスオーディオコーデック）
3. .mp3

ファイルフォーマットは、オーディオ信号のデジタル表現を圧縮する方法によって区別されます

変換の手順 —

• マイクはアナログ信号をキャプチャします。
• 音波は次に電気信号に変換されます。
• この電気信号は、アナログ-デジタル変換器によってデジタル化されます。

サンプリング

• 信号の値を固定された時間ステップで計測するプロセスです
• 一度サンプリングされると、サンプルされた波形は離散形式になります

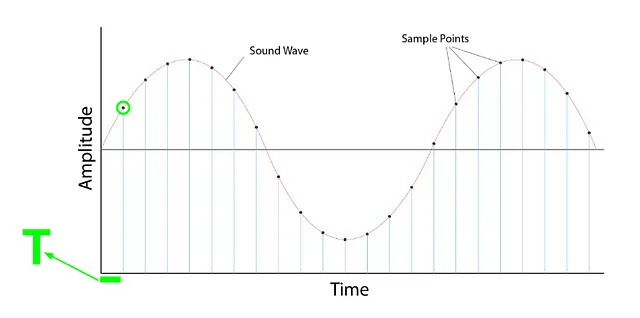
サンプリングレート/ サンプリング周波数

• 1秒あたりに取られるサンプル数
• 例：1秒あたりに1000サンプルが取られる場合、サンプリングレート（SR）= 1000
• 高いSR -> 高品質なオーディオ

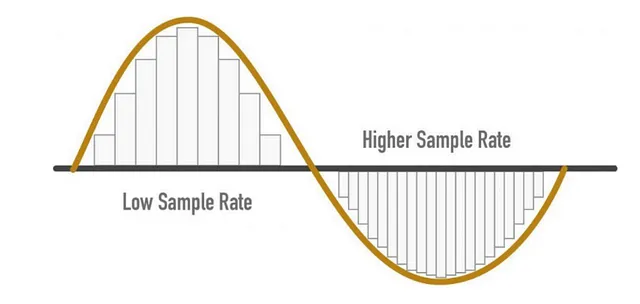
SRの考慮事項

• サンプリングレート=（信号からキャプチャできる最高周波数）* 2
• 人間の耳には聞こえる周波数が8KHzありますので、サンプリングレート（SR）は16KHzと言えます
• より高いSRは音声品質が向上するが、それを無限に増やす必要はない
• 必要なラインを超えると、情報は追加されず、計算コストだけが増える
• また、低いSRは情報の損失を引き起こす場合があります

覚えておくべきポイント —

• トレーニング中にすべてのオーディオサンプルは同じサンプリングレートを持つようにする
• 事前にトレーニングされたモデルを使用する場合、オーディオサンプルはトレーニングデータモデルのSRに一致するようにリサンプリングする必要があります
• 異なるSRのデータを使用すると、モデルはうまく一般化しない可能性があります

振幅 —

• 音は、人間が聞こえる周波数での気圧の変化によって作られます
• 振幅 — その瞬間の音圧レベルをdB（デシベル）で測定したもの
• 振幅は音量の尺度です

ビットの深さ —

• どれくらいの精度で値を表現できるかを示します
• ビットの深さが高ければ高いほど、デジタル表現が元の連続的な音波に近くなります
• 一般的なビットの深さの値は16ビットと24ビットです

量子化 —

最初に、音声は連続的な形であり、滑らかな波です。デジタルで保存するためには、小さなステップで保存する必要があります。そのために量子化を行います。

• 「Retroformer」をご紹介します：プラグインの回顧モデルを学習することで、大規模な言語エージェントの反復的な改善を実現する優れたAIフレームワーク
• 「集団行動のデコード：アクティブなベイズ推論が動物グループの自然な移動を支える方法」
• このAI論文では、これらの課題に対処しながらMoEsの利点を維持するために、完全に微分可能な疎なTransformerであるSoft MoEを提案しています

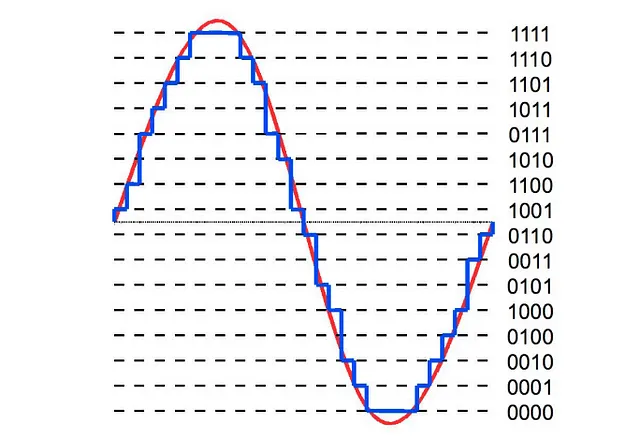
ビットの深さは、音声を表現するために必要なステップの数と言えます

• 16ビット音声は — 65536ステップが必要です
• 24ビット音声は — 16777216ステップが必要です
• この量子化はノイズを発生させます。そのため、高いビットの深さが好まれます
• ただし、このノイズは問題ありません
• 16ビットと24ビット音声はintサンプルに、32ビット音声は浮動小数点で保存されます
• モデルは浮動小数点を必要とするため、モデルをトレーニングする前にこの音声を浮動小数点に変換する必要があります

実装 —

#ライブラリを読み込むimport librosa

#librosa.load関数は、音声配列とサンプリングレートを返しますaudio、sampling_rate = librosa.load(librosa.ex('pistachio'))

import matplotlib.pyplot as pltplt.figure().set_figwidth(12)librosa.display.waveshow(audio,sr = sampling_rate)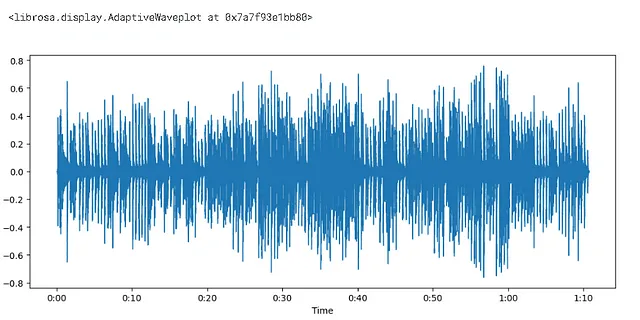

• 振幅はy軸に、時間はx軸にプロットされました
• 範囲は[-1.0,1.0] — 既に浮動小数点の数値です

print(len(audio))print(sampling_rate/1e3)>>1560384>>22.05

## 周波数スペクトルimport numpy as np#各離散値に焦点を当てる代わりに、最初の4096個の値を見てみましょうinput_data = audio[:4096]# DFT = 離散フーリエ変換# この周波数スペクトルはDFTを使用してプロットされますwindow = np.hanning(len(input_data))window>>array([0.00000000e+00, 5.88561497e-07, 2.35424460e-06, ...,       2.35424460e-06, 5.88561497e-07, 0.00000000e+00])

dft_input = input_data * window

figure = plt.figure(figsize = (15,5))plt.subplot(131)plt.plot(input_data)plt.title('input')plt.subplot(132)plt.plot(window)plt.title('hanning window')plt.subplot(133)plt.plot(dft_input)plt.title('dft_input')# 同様のプロットが各インスタンスごとに生成されます

離散周波数変換 = DFT

• 離散信号データがあると言ったら、私の意見に同意していただけますか？
• もし同意していただけるのであれば、それは今まで時間領域のデータを持っていたということであり、今は周波数領域に変換したいということです。DFTが助けてくれる理由です。

# DFT（離散フーリエ変換）を計算するdft = np.fft.rfft(dft_input)plt.plot(dft)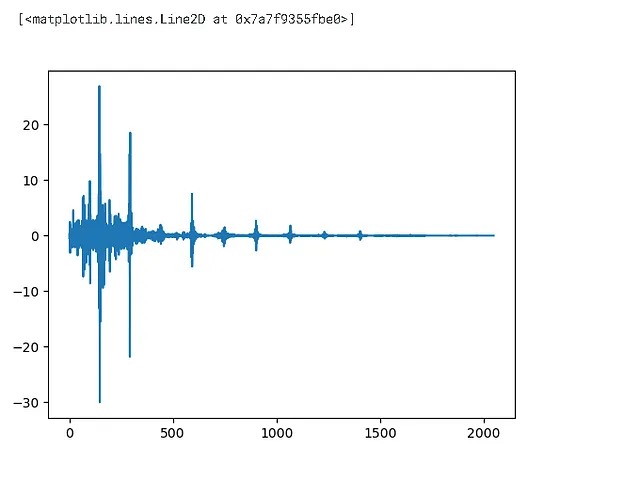

# 振幅振幅 = np.abs(dft)# dBに変換amplitude_dB = librosa.amplitude_to_db(amplitude,ref = np.max)# パワースペクトルを使用したい場合もあります -> A**2

なぜ絶対値を取るのですか？

振幅を取るときには、絶対値を適用しました。その理由は複素数

• フーリエ変換後の出力は複素形式であり、絶対値を取ることで大きさを得ることができました。

print(len(amplitude))print(len(dft_input))print(len(dft))>>2049>>4096>>2049

なぜ更新された配列は元の配列の半分+1なのですか？

純粋に実数入力の場合、DFTはエルミート対称であり、負の周波数成分は対応する正の周波数成分の複素共役であり、したがって負の周波数成分は冗長です。この関数では負の周波数成分を計算せず、変換された軸の長さはn//2 + 1です。[出典 – ドキュメント]

# 周波数frequency = librosa.fft_frequencies(n_fft=len(input_data),sr = sampling_rate)

plt.figure().set_figwidth(12)plt.plot(frequency, amplitude_dB)plt.xlabel("Frequency (Hz)")plt.ylabel("Amplitude (dB)")plt.xscale("log")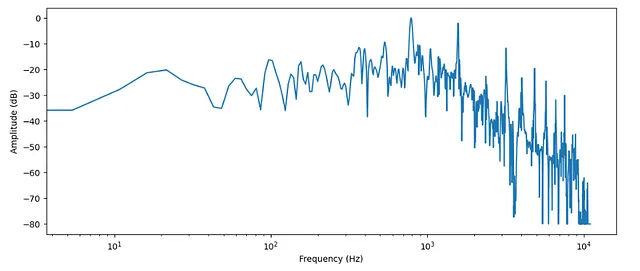

• 先に述べたように、時間領域 -> 周波数領域
• 周波数領域は通常、対数スケールでプロットされます

スペクトログラム —

• 周波数の変化を時間に対して表示します
• この変換を行うアルゴリズムは、ソフト=短時間フーリエ変換です

スペクトログラムの作成方法 —

• スペクトログラムは、周波数変換のスタックです。どのようにして作成するか見てみましょう
• 与えられたオーディオに対して、小さなセグメントを取り、その周波数スペクトルを見つけます。その後、それらを時間軸に沿って積み重ねるだけです。結果の図はスペクトログラムです
• librosa.stftはデフォルトで2048のセグメントに分割します

周波数スペクトル —

• ある瞬間の異なる周波数の振幅を表します。
• 周波数スペクトルは、特定の瞬間における信号の周波数成分を理解するためにより適しています。両方の表現は、信号の周波数領域の特性を理解するための有用なツールです。
• 振幅 vs. 周波数

スペクトログラム —

• 信号をセグメントに分割し、時間の経過に伴う周波数スペクトルをプロットすることで、周波数内容の変化を表します。
• スペクトログラムは、特にオーディオ信号や時系列データなどの時間変動する信号を分析および視覚化するために非常に有用です。異なる時間間隔で周波数成分がどのように変化するかを示しています。
• 周波数 vs. 時間

spectogram = librosa.stft(audio)
spectogram_to_dB = librosa.amplitude_to_db(np.abs(spectogram), ref=np.max)

plt.figure().set_figwidth(12)
librosa.display.specshow(spectogram_to_dB, x_axis="time", y_axis="hz")
plt.colorbar()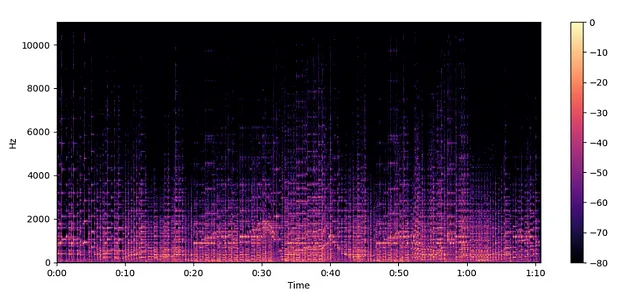

メルスペクトログラム —

• 異なる周波数スケールでのスペクトログラム。

進む前に、覚えておくべきことがあります。

• 低い周波数では、高い周波数よりも人間は音の変化に対してより敏感です。
• この感度は、周波数の増加と対数的に変化します。
• したがって、単純に言えば、メルスペクトログラムはスペクトログラムの圧縮バージョンです。

MelSpectogram = librosa.feature.melspectrogram(y=audio, sr=sampling_rate, n_mels=128, fmax=8000)
MelSpectogram_dB = librosa.power_to_db(MelSpectogram, ref=np.max)
plt.figure().set_figwidth(12)
librosa.display.specshow(MelSpectogram_dB, x_axis="time", y_axis="mel", sr=sampling_rate, fmax=8000)
plt.colorbar()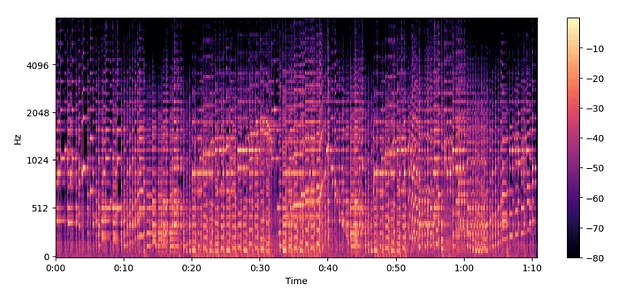

• 上記の例では、librosa.feature.melspectrogram() がパワースペクトログラムを作成するために使用され、librosa.power_to_db()が使用されています。

結論 —

メルスペクトログラムは通常のスペクトログラムよりも意味のある特徴を捉えるので、人気があります。

参考文献 —

Huggingface

個人のKaggleカーネル（練習用）

Socials —

LinkedIn

Kaggle

この記事が気に入ったら、拍手で感謝の気持ちを示すのを忘れないでください。次のノートブックでお会いしましょう、「オーディオデータの読み込みとストリーミング方法」を見ていきます。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!