「バイアス調整の力を明らかにする：不均衡なデータセットにおける予測精度の向上」

Improving Prediction Accuracy in Imbalanced Datasets Revealing the Power of Bias Adjustment

データサイエンスにおいて、クラスの不均衡を解消することは正確な予測にとって重要です。この記事では、クラスの不均衡に対応してモデルの正確性を向上させるためのバイアス調整について紹介します。バイアス調整が予測を最適化し、この課題を克服する方法について探求します。

イントロダクション

データサイエンスの領域では、不均衡なデータセットを効果的に管理することが正確な予測にとって重要です。不均衡なデータセットは、クラスの格差が大きい特徴を持ち、詐欺検出や疾病診断などの重要な文脈で、多数派のクラスを好むバイアスのかかったモデルを生み、少数派のクラスに対しては性能が低下する可能性があります。

この記事では、バイアス調整という実用的な解決策を紹介します。モデル内のバイアス項を微調整することで、バイアス調整はクラスの不均衡を打破し、多数派と少数派の両方のクラスに対する正確な予測能力を向上させます。記事では、二値分類と多クラス分類に対応したアルゴリズムを概説し、それらの基本原理について探求します。特に、アルゴリズムの説明と基本原理のセクションでは、私のアルゴリズム、過剰サンプリング、クラスの重みの調整の間に理論的な関連性を厳密に確立し、読者の理解を向上させます。

効果と理論的根拠を裏付けるために、シミュレーション研究ではバイアス調整と過剰サンプリングの関係を詳細に検討します。さらに、クレジットカード詐欺検出におけるバイアス調整の実装と具体的な利点を示すために実践的なアプリケーションを使用します。

• このAI研究は、パーソン再識別に適したデータ拡張手法であるStrip-Cutmixを提案しています
• データサイエンスのためのLinux VMをスーパーチャージングする：改善されたパフォーマンスのためのLinux VM RAMの強化ガイド
• 「Pythonベクトルデータベースとベクトルインデックス：LLMアプリの設計」

バイアス調整は、クラスの不均衡に対処するための予測モデリング結果を改善するための直接的で効果的な手段を提供します。この記事は、バイアス調整のメカニズム、原則、および現実世界での影響について包括的な理解を提供し、不均衡なデータセットにおけるモデルのパフォーマンスを向上させたいデータサイエンティストにとって貴重なツールです。

アルゴリズム

バイアス調整アルゴリズムは、二値分類と多クラス分類のタスクにおけるクラスの不均衡に対処する手法を紹介します。アルゴリズムは各エポックでバイアス項を再調整することにより、モデルが効果的に不均衡なデータセットを処理する能力を向上させます。バイアス項を調整することで、アルゴリズムは少数派クラスのインスタンスに敏感になり、分類の正確性を向上させます。

モデル f(x) と予測における役割

バイアス調整アルゴリズムの核心となるのは、f(x) という概念です。f(x) は、入力特徴 x と最終的な予測との間の重要な要素です。二値分類では、f(x) は入力を実数値に変換するマッピングとして機能し、確率解釈のためのシグモイド活性化と整合します。多クラス分類では、f(x) は f_k​(x) のセットの関数に変換され、各クラス k には独自の関数があり、ソフトマックス活性化と連動して動作します。この違いは、バイアス調整アルゴリズムで重要であり、f(x) を使用してバイアス項を調整し、クラスの不均衡に対する感度を微調整します。

アルゴリズムの概要

アルゴリズムの概念はシンプルです。各クラス k の f_k​(x) の平均を計算し、この平均を δk​ として表します。f_k​(x) から δk​ を減算することで、f_k​(x) − δk​ の期待値がすべてのクラス k に対して0になるようにします。その結果、モデルは各クラスが同様に発生する可能性があると予測します。このアプローチはアルゴリズムの論理的および数学的な基盤で裏付けられていることに留意することが重要です。これについては、この記事の後続のセクションで詳しく探求されます。

二値分類のためのアルゴリズム

予測のための利用: 予測を行うためには、アルゴリズムから最後に計算された δ の値を適用します。この δ の値はトレーニング中に行われた累積的な調整を反映し、予測時のシグモイド活性化関数における最終的なバイアス項の基礎となります。

多クラスのためのアルゴリズム

予測の利用：アルゴリズムのトレーニングプロセスの集大成として、最後に計算されたδkの値が得られます。このδkの値は、トレーニング中に入念に調整された累積バイアス項の調整をカプセル化しています。その重要性は、予測時のソフトマックス活性化関数の最終バイアス項の基本パラメータとしての役割にあります。

アルゴリズムの説明と基本原則

オーバーサンプリングからクラスの重み調整へ、クラスの重み調整から新しいアルゴリズムへ

このセクションでは、アルゴリズムの説明と基本原則について探求します。アルゴリズムの操作のメカニクスと理論的根拠を明らかにし、分類タスクにおけるクラスの不均衡に対処する効果についての洞察を提供します。

損失関数と不均衡

まず、アルゴリズムの核心である損失関数について探求します。初めの説明では、クラスの不均衡の問題を直接的には考慮しません。クラス1が観測の90％を占め、クラス0が残りの10％を構成するバイナリ分類問題を考えてみましょう。クラス1の観測値の集合をC1、クラス0の観測値の集合をC0とし、これを出発点とします。

クラスの不均衡を考慮しない場合、損失関数は次のようになります：

モデルの推定を追求するために、この損失関数を最小化しようとします：

不均衡の緩和：オーバーサンプリングとクラスの重み調整

しかし、私たちの努力の核心は、クラスの不均衡の問題に取り組むことにあります。この課題を克服するために、オーバーサンプリング技術を利用します。さまざまなオーバーサンプリング手法が存在しますが、シンプルなオーバーサンプリング、ランダムオーバーサンプリング、SMOTEなどに焦点を絞り、現在の明瞭さを持って説明します。

シンプルなオーバーサンプリング：私たちのアーセナルにおける基本的なアプローチはシンプルなオーバーサンプリングです。この手法では、少数クラスのインスタンスを多数クラスのサイズに合わせるために、少数クラスのインスタンスを8倍に複製します。この例では、少数クラスが10％、多数クラスが残りの90％を構成している場合、少数クラスの観測値を8倍に複製し、クラスの分布を均等化します。複製された観測値の集合をD0とし、この手順により損失関数が次のように変換されます：

これは深い洞察を示しています：シンプルなオーバーサンプリングの核心原理は、クラスの重み調整の概念にシームレスに対応していることがわかります。少数クラスを8倍に複製することは、実質的に少数クラスの重みを9倍に増やすことに相当します。重要なのは、オーバーサンプリングの技術が重み調整のメカニズムに対応していることです。

ランダムオーバーサンプリング：ランダムオーバーサンプリングについての短い考察は、同様の観察を補強します。ランダムオーバーサンプリングは、よりシンプルな相手と同様に、観測値の重みをランダムに調整することに相当します。

クラスの重み調整からバイアス調整へ

私たちのアプローチの核心であるバイアス調整、オーバーサンプリング、重み調整の間の本質的な同等性が明らかになります。この洞察は、

“Prentice and Pyke (1979) … have shown that, when the model contains a constant (intercept) term for each category, these constant terms are the only coefficient affected by the unequal selection probability of the Y” Scott & Wild (1986) [2]. Also, Manski and Lerman (1977) show the same result in softmax setting [1].

意義の明示：機械学習の領域において、定数（切片）項はバイアス項となります。この基本的な観察結果から、クラスの重みや観測の重みを再調整すると、その結果として主にバイアス項が調整されます。要するに、バイアス項はクラスの不均衡に対処するための戦略を結びつける要素となります。

統一的な視点

この理解により、アルゴリズム、オーバーサンプリング、重みの調整は、本質的には同等で交換可能であることが明確になります。この統一化により、クラスの不均衡の課題を緩和する方法を簡素化することができます。

シミュレーション研究：オーバーサンプリングによるバイアス項の影響の検証

モデルの機能的な核心を変えずに、オーバーサンプリングが主にバイアス項に影響を与えることを確かめるために、対象となるシミュレーション研究に深入りします。オーバーサンプリング手法がモデルの本質を変えずにバイアス項に影響を与えることを経験的に示すことを目指します。

シミュレーションのセットアップ

この説明のために、簡略化されたシナリオに焦点を当てます：単一の特徴を持つロジスティック回帰です。モデルは次のように定義されます：

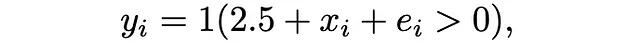
ここで、1(.)は指示関数を示し、x_iは標準正規分布から引かれ、e_iはロジスティック分布に従います。この文脈では、f(x)=xと設定しています。

シミュレーションの実行：

このセットアップを使用して、オーバーサンプリング手法がバイアス項に与える影響を詳細に検証しますが、モデルの核心は一定のままです。3つのオーバーサンプリング手法を使用します：シンプルオーバーサンプリング、SMOTE、およびランダムサンプリング。それぞれの手法を注意深く適用し、結果を注意深く記録します。

以下のPythonコードスニペットは、シミュレーションプロセスの概要を示しています：

# パッケージの読み込みimport numpy as npimport statsmodels.api as smfrom imblearn.over_sampling import SMOTE, RandomOverSampler# シードの設定np.random.seed(1)# シミュレーションデータの作成x = np.random.normal(size = 10000)y = (2.5 + x + np.random.logistic(size = 10000)) > 0# バイアス項は2.5、xの係数は1に設定# クラス1のサイズは9005print(sum(y == 1))# クラス0のサイズは995print(sum(y == 0))# クラス0のサイズをクラス1に合わせるようにする# 方法0 何もしないx0 = xy0 = ymethod0 = sm.Logit(y0, sm.add_constant(x0)).fit()print(method0.summary())  # バイアス項は2.54、x3の係数は0.97# 方法1 シンプルオーバーサンプリングx1 = np.concatenate((x, np.repeat(x[y == 0], 8)))y1 = np.concatenate((y, np.array([0] * (len(x1) - len(x)))))method1 = sm.Logit(y1, sm.add_constant(x1)).fit()print(method1.summary())  # バイアス項は0.35、x3の係数は0.98# 方法2 SMOTEsmote = SMOTE(random_state = 1)x2, y2 = smote.fit_resample(x[:, np.newaxis], y)method2 = sm.Logit(y2, sm.add_constant(x2)).fit()print(method2.summary())  # バイアス項は0.35、x3の係数は1# 方法3 ランダムサンプリングrandom_sampler = RandomOverSampler(random_state=1)x3, y3 = random_sampler.fit_resample(x[:, np.newaxis], y)method3 = sm.Logit(y3, sm.add_constant(x3)).fit()print(method3.summary()) # バイアス項は0.35、x3の係数は0.99

結果：

主な観察結果

シミュレーション研究の結果は、私たちの提案を簡潔に裏付けています。さまざまなオーバーサンプリング手法を適用しても、コアモデル関数 f(x)=x は変わりません。重要な洞察は、すべてのオーバーサンプリング手法におけるモデルの成分の驚くほどの一貫性にあります。代わりに、バイアス項には顕著な変動が見られ、オーバーサンプリングが主にバイアス項に影響を与え、基礎となるモデル構造には影響を与えないことを裏付けています。

コアコンセプトの強化

私たちのシミュレーション研究は、オーバーサンプリング、重み調整、およびバイアス項の修正の基本的な等価性を明確に強調しています。オーバーサンプリングがバイアス項のみを変更することを示すことで、これらの戦略がクラスの不均衡に対する交換可能なツールである原則を強化しています。

バイアス調整アルゴリズムをクレジットカード詐欺検知に適用する

クラスの不均衡を解消するためのバイアス調整アルゴリズムの効果を示すために、クレジットカード詐欺検知に焦点を当てたKaggleコンペティションの実世界のデータセットを使用します。このシナリオでは、詐欺事件の希少性があるため、クレジットカードの取引が詐欺であるか（ラベル1）であるか、詐欺でないか（ラベル0）を予測することが課題です。

必要なパッケージを読み込み、データセットを準備します：

import numpy as npimport pandas as pdimport tensorflow as tfimport tensorflow_addons as tfafrom sklearn.model_selection import train_test_splitfrom imblearn.over_sampling import SMOTE, RandomOverSampler# データセットの読み込みと前処理df = pd.read_csv("/kaggle/input/playground-series-s3e4/train.csv")y, x = df.Class, df[df.columns[1:-1]]x = (x - x.min()) / (x.max() - x.min())x_train, x_valid, y_train, y_valid = train_test_split(x, y, test_size=0.3, random_state=1)batch_size = 256train_dataset = tf.data.Dataset.from_tensor_slices((x_train, y_train)).shuffle(buffer_size=1024).batch(batch_size)valid_dataset = tf.data.Dataset.from_tensor_slices((x_valid, y_valid)).batch(batch_size)

次に、バイナリ分類のためのシンプルなディープラーニングモデルを定義し、オプティマイザ、損失関数、評価指標を設定します。コンペティションの評価に従い、評価指標としてAUCを選択します。さらに、この記事の焦点はバイアス調整アルゴリズムの実装方法を示すことであり、予測の優位性を示すことではないため、意図的にモデルを簡略化しています：

model = tf.keras.Sequential([    tf.keras.layers.Normalization(),    tf.keras.layers.Dense(32, activation='swish'),    tf.keras.layers.Dense(32, activation='swish'),    tf.keras.layers.Dense(1)])optimizer = tf.keras.optimizers.Adam()loss = tf.keras.losses.BinaryCrossentropy()val_metric = tf.keras.metrics.AUC()

バイアス調整アルゴリズムの中核には、トレーニングステップとバリデーションステップがあり、クラスの不均衡を緻密に扱います。このプロセスを明確にするために、モデルの予測をバランスさせるための複雑なメカニズムについて詳しく説明します。

デルタ値を累積するトレーニングステップ

トレーニングステップでは、クラスの不均衡に対するモデルの感度を向上させる旅に乗り出します。ここでは、2つの異なるクラスター、delta0とdelta1のモデル出力の合計を計算し、累積します。これらのクラスターは重要な意味を持ち、それぞれクラス0およびクラス1に関連する予測値を表しています。

# トレーニングステップ関数の定義@tf.functiondef train_step(x, y):    delta0, delta1 = tf.constant(0, dtype = tf.float32), tf.constant(0, dtype = tf.float32)    with tf.GradientTape() as tape:        logits = model(x, training=True)        y_pred = tf.keras.activations.sigmoid(logits)        loss_value = loss(y, y_pred)        # クラスの不均衡を解消するための新しいバイアス項の計算        if len(logits[y == 1]) == 0:            delta0 -= (tf.reduce_sum(logits[y == 0]))        elif len(logits[y == 0]) == 0:            delta1 -= (tf.reduce_sum(logits[y == 1]))        else:            delta0 -= (tf.reduce_sum(logits[y == 0]))            delta1 -= (tf.reduce_sum(logits[y == 1]))    grads = tape.gradient(loss_value, model.trainable_weights)    optimizer.apply_gradients(zip(grads, model.trainable_weights))    return loss_value, delta0, delta1

検証ステップ：デルタによる不均衡解消

トレーニングプロセスから派生した正規化されたデルタ値が、検証ステップで中心的な役割を果たします。これらの洗練されたクラス不均衡の指標を武器に、モデルの予測を真のクラス分布とより正確に合わせます。 test_step 関数はこれらのデルタ値を統合し、適応的に予測を調整し、最終的に洗練された評価を行います。

@tf.functiondef test_step(x, y, delta):    logits = model(x, training=False)    y_pred = tf.keras.activations.sigmoid(logits + delta)  # デルタで予測を調整    val_metric.update_state(y, y_pred)

不均衡補正におけるデルタ値の活用

トレーニングが進むにつれて、delta0 と delta1 のクラスターの総和に内包された貴重な洞察を収集します。これらの累積値は、モデルの予測に内在するバイアスの指標として現れます。各エポックの終わりに、重要な変換を実行します。各クラスの対応する観測数で累積クラスターの総和を割ることで、正規化されたデルタ値を求めます。この正規化は重要な均一化器として機能し、バイアス調整手法の本質を包括的に表現します。

E = 1000P = 10B = len(train_dataset)N_class0, N_class1 = sum(y_train == 0), sum(y_train == 1)early_stopping_patience = 0best_metric = 0for epoch in range(E):    # デルタの初期化    delta0, delta1 = tf.constant(0, dtype = tf.float32), tf.constant(0, dtype = tf.float32)    print("\nStart of epoch %d" % (epoch,))    # データセットのバッチを反復処理する    for step, (x_batch_train, y_batch_train) in enumerate(train_dataset):        loss_value, step_delta0, step_delta1 = train_step(x_batch_train, y_batch_train)        # デルタの更新        delta0 += step_delta0        delta1 += step_delta1    # すべてのデルタ値の平均を取る    delta = (delta0/N_class0 + delta1/N_class1)/2        # 各エポックの終わりに検証ループを実行する    for x_batch_val, y_batch_val in valid_dataset:        test_step(x_batch_val, y_batch_val, delta)    val_auc = val_metric.result()    val_metric.reset_states()    print("Validation AUC: %.4f" % (float(val_auc),))    if val_auc > best_metric:        best_metric = val_auc        early_stopping_patience = 0    else:        early_stopping_patience += 1        if early_stopping_patience > P:        print("早期停止の忍耐力に達しました。検証AUC：%.4fでトレーニング終了" % (float(best_metric),))        break;

結果

クレジットカード詐欺検出への応用において、アルゴリズムの向上した効果が光ります。バイアス調整がトレーニングプロセスにシームレスに統合されることで、0.77の印象的なAUCスコアを達成します。これは、バイアス調整の指導のない場合に達成された0.71のAUCスコアとは明確に異なります。予測性能の深い改善は、クラスの不均衡の複雑さを乗り越えるアルゴリズムの能力を証明するものです。

参考文献

[1] Manski, C. F., & Lerman, S. R. (1977). The estimation of choice probabilities from choice based samples. Econometrica: Journal of the Econometric Society, 1977–1988.

[2] Scott, A. J., & Wild, C. J. (1986). Fitting logistic models under case-control or choice based sampling. Journal of the Royal Statistical Society Series B: Statistical Methodology, 48(2), 170–182.

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!