「カオスから秩序へ：データクラスタリングを活用した意思決定の向上」

Improving decision-making with data clustering From chaos to order

この記事では、データクラスタリング手法の重要なユースケース、これらの手法の使用方法、およびこれらの手法を次元削減の手法として使用する方法を示します。

まず、これらの手法が人気を集める使用例について説明しましょう。

顧客セグメンテーション

オンラインストアは、購入パターン、購入日、年齢、所得など、さまざまな要素に基づいて顧客をクラスタリングするためにこの手法を使用しています。これにより、ストアは顧客をより良く理解し、高い利益を確保するための意思決定に役立ちます。

より明確に理解するために、具体例を挙げましょう。例えば、購入日と年齢に基づいて顧客をクラスタリングした結果、22歳未満の人々が月末にはかなり少ない金額しか使わないことがわかったとします。22歳未満の人々の多くは学生であり、月末は経済的に厳しいため、ストアを訪れることをためらうかもしれません。そこで、ストアは学生層を引きつけるために月末の割引セールを実施することで、これをストアの利益に活かすことができます。

• GOAT-7B-Communityモデルをご紹介します：GoatChatアプリから収集されたデータセットでLLaMA-2 7Bモデルを微調整したAIモデルです
• FraudGPT AIを活用したサイバー犯罪ツールの驚異的な台頭
• SQLからJuliaへ：データサイエンスの他のプログラミング言語

このような解決策をクラスタリングを使用しなかった場合、ストアは見つけることができなかったかもしれません。

このTableauダッシュボードでもクラスタリングの別の例を見つけることができます。

データ分析のために

データを全体ではなく、それぞれのクラスタごとに分析することで、いくつかの興味深い結果が得られることがあります。

次元削減の手法として

クラスタリング手法は次元削減手法としても使用することができます。この方法については、記事の最後で説明します。

半教師あり学習

データをクラスタリングし、その後、各クラスタごとに別々のモデルをトレーニングすることで、機械学習モデルの精度を向上させることができます。

分類問題に対して半教師あり学習手法を使用する場合、一つのクラスタに同じラベルのインスタンスが存在することがあります。このような状況に対処するために、入力されたすべてのインスタンスに同じラベルを返すモデルを作成することができます。

このアプローチは、私のプロジェクトの一つで使用されています。プロジェクトのソースコードは、私のGithubアカウントでご覧いただけます。

その他の使用例

上記の使用例以外にも、クラスタリングは画像のセグメンテーションなどに非常に役立ちます。

さて、いくつかの有名なクラスタリング手法を見てみましょう。

KMeansクラスタリング

KMeansは、最も有名なクラスタリング手法の一つです。この手法は、各インスタンスをブロブの中心に割り当てることを試みます。

この手法の動作を見てみましょう。

まず、ランダムにセントロイドを配置してください。次に、各クラスタにラベルを付けます。その後、すべてのインスタンスにラベルを割り当てます。インスタンスは、最も近いセントロイドに属するクラスタのラベルを受け取ります。その後、セントロイドを再度更新します。これを繰り返し行い、セントロイドに変化がなくなるまで繰り返します。

このアルゴリズムは収束することが保証されていますが、最適な解には収束しない場合があります。正しい解に収束するかどうかは、セントロイドの初期化、つまりアルゴリズムの開始時に使用するセントロイドの座標に依存します。

この問題への解決策の一つは、異なるランダムなセントロイドの初期化を使用してアルゴリズムを複数回実行し、最良の解を保持することです。最良の解は、慣性として知られるパフォーマンス指標によって見つけられます。これは、各インスタンスと最も近いセントロイドとの平均二乗距離です。

この問題へのより一般的な解決策もあります。この解決策を実装した新しいアルゴリズムは、KMeans++として知られています。

これは、互いに離れたセントロイドを選択する傾向がある新しい初期化ステップを導入し、この改良によりkMeansアルゴリズムはサブオプティマルな解に収束する可能性が大幅に低くなりました。

KMeansアルゴリズムには、高速化されたKMeansやミニバッチKMeansなど、さまざまなバリエーションがあります。

Scikit-Learnライブラリの組み込みクラスを使用して、このアルゴリズムを簡単に実装することができます。ただし、本当の課題は、データを完全に分離するための最適なクラスタの数を見つけることです。

最適なクラスタの数を見つける

最適なクラスタの数を見つけるために使用できる2つのメソッドがあります：

1. エルボー法とシルエットスコアを使用する
2. kneed Pythonライブラリを使用する

エルボー法とシルエットスコアの使用

エルボー法は、慣性とクラスタの数のプロットの間のエルボーを見つけることです。慣性の値は、高すぎず低すぎずであることを望みます。一般的に、そのような値は慣性vsクラスタ数のプロットのエルボーに位置しています。

Scikit-learnライブラリを使用してシルエットスコアを見つけることができます。シルエットスコアは-1から1までの範囲にあります。

シルエットスコアが1に近い場合、インスタンスは自分自身のクラスタ内にあり、他のクラスタから遠いことを意味します。シルエットスコアが0に近い場合、クラスタ境界に近いことを意味します。シルエットスコアが-1に近い場合、インスタンスは間違ったクラスタに割り当てられている可能性があります。

したがって、慣性が高すぎず低すぎずであること、またシルエットスコアも適切であることを考慮して、最適なクラスタの数を見つけます。

どのように行うかを見てみましょう。

## 必要なインポートimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport seaborn as sns## データの読み込み"""デモンストレーション用に、ウェイターが受け取ったチップの量を、週の日、食事の時間、合計請求額などのさまざまな要因に基づいて表示する単純なデータセットを使用します。"""df = pd.read_csv('https://raw.githubusercontent.com/mwaskom/seaborn-data/master/tips.csv')df.head()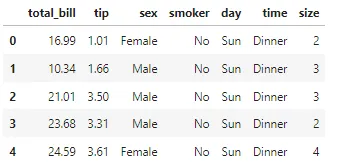

## 合計請求額とチップのプロットplt.figure(figsize=(12,8))sns.set_style('darkgrid')plt.plot(df['total_bill'], df['tip'], 'bo')plt.xlabel('合計請求額')plt.ylabel('チップ')plt.title('合計請求額 VS チップ')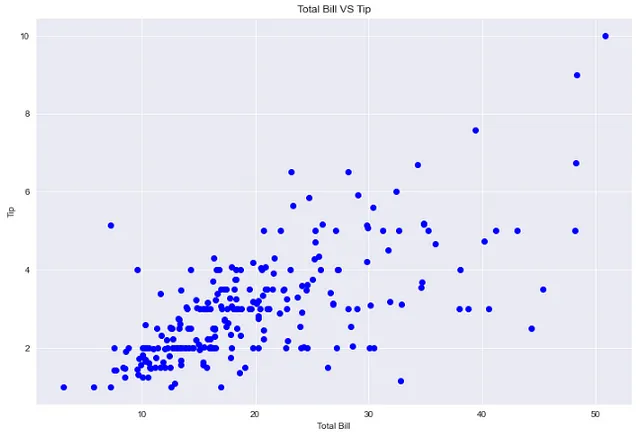

## total_bill、tip、size列を使用してデータフレームをクラスタリングする## エルボー法を使用して最適なクラスタの数を見つけるために"""慣性とクラスタ数の関係をプロットするために、異なるクラスタ数でいくつかのクラスタリングモデルをトレーニングします。これらのモデルの各々について、慣性を記録します。最後に、記録された慣性を使用してグラフを作成します。"""from sklearn.cluster import KMeansinertia_list = [KMeans(n_clusters=i).fit(df[['total_bill','tip']]).inertia_ for i in range(2,10)]plt.figure(figsize=(12,8))sns.set_style('darkgrid')plt.plot(list(range(2,10)),inertia_list, 'rx', ls='solid')plt.xlabel('クラスタの数')plt.ylabel('慣性')plt.title('エルボー法を使用した最適なクラスタの数の見つけ方')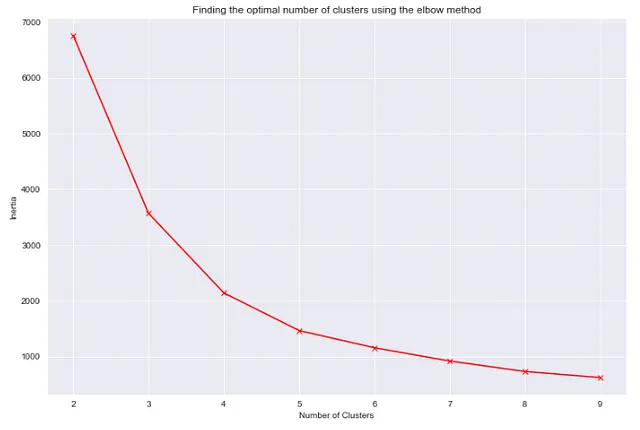

プロットによれば、最適なクラスタの数は4または5であるべきです。これらの2つの値の慣性値は、高すぎず低すぎません。

## シルエットスコアを使用して最適なクラスタの数を見つけるためにfrom sklearn.metrics import silhouette_score"""慣性とクラスタ数の関係をプロットする際と同様のプロセスを使用して、シルエットスコアvsクラスタ数のプロットを作成します。"""sil_score_list = []for i in range(2,10):    kmeans = KMeans(n_clusters=i)    kmeans.fit(df[['total_bill','tip']])    sil_score_list.append(silhouette_score(df[['total_bill','tip']],kmeans.labels_))plt.figure(figsize=(12,8))sns.set_style('darkgrid')plt.plot(list(range(2,10)),sil_score_list, 'mx', ls='solid')plt.xlabel('クラスタの数')plt.ylabel('シルエットスコア')plt.title('シルエットスコアを使用した最適なクラスタの数の見つけ方')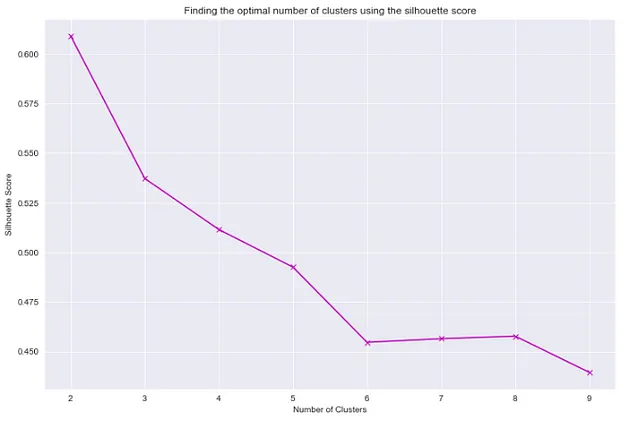

上記の2つのプロットによると、クラスタの数が4である場合、十分なシルエットスコアと良好な慣性値を得ることができます。したがって、クラスタリングの良好なパフォーマンスを求めるために4つのクラスタを使用できます。

kneed Pythonライブラリを使用

## kneedライブラリを使用してkmeansモデルの最適なクラスタ数を見つけるfrom kneed import KneeLocatorkn = KneeLocator(range(2,10), inertia_list, curve='convex',direction='decreasing')print(f"kmeansモデルの最適なクラスタ数：{kn.knee}")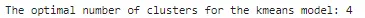

kneedライブラリも最初のメソッドと同じクラスタ数の値を返しました。これでデータを4つのクラスタに分割して、クラスタを視覚化しましょう。

## クラスタリングのためにクラスタ数4を使用kmeans_final = KMeans(n_clusters=4)kmeans_final.fit(df[['total_bill','tip']])pred = kmeans_final.predict(df[['total_bill','tip']])## クラスタラベルのための新しい列の作成df['cluster'] = pred## クラスタの視覚化 ## クラスタリング後のデータのプロットsns.set_style('whitegrid')sns.jointplot(x='total_bill', y='tip', data=df, hue='cluster',palette='coolwarm');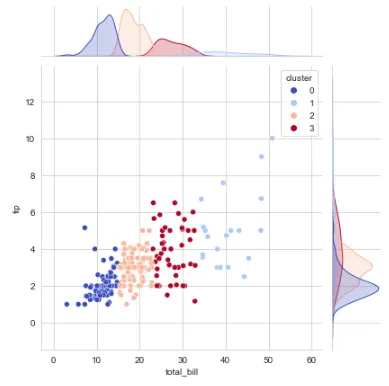

DBSCANクラスタリング

このアルゴリズムは、低密度地域によって分離された高密度領域の連続的な領域をクラスタと定義します。そのため、DBSCANによるクラスタリングは、凸形状のクラスタを与えるKMeansとは異なる形状のクラスタを取ることができます。

DBSCANアルゴリズムの最も重要なコンポーネントは、コアサンプルの概念です。コアサンプルは、高密度領域に存在するインスタンスです。したがって、DBSCANアルゴリズムにおけるクラスタとは、お互いに近接しているコアサンプルの集合と、コアサンプルに近接している非コアサンプルの集合です。Scikit-LearnのDBSCANクラスを使用して簡単にDBSCANアルゴリズムを実装することができます。このクラスには2つの重要なパラメータ、min_samplesとepsがあります。これらは、密度を定義するために何を意味するかを定義します。

各インスタンスについて、アルゴリズムは小さな距離eps内にいくつのインスタンスがあるかを数えます。この領域はインスタンスのeps-近傍と呼ばれます。

インスタンスが少なくともmin_samples個のインスタンスをそのeps-近傍に持つ場合（それ自体を含む）、それはコアインスタンスと見なされます。コアインスタンスの近傍にあるすべてのインスタンスは同じクラスタに属します。この近傍には他のコアインスタンスも含まれるため、単一のクラスタからのコアインスタンスの長い連続したシーケンスが存在するかもしれません。

ここでは、KMeansクラスタリングに使用したデータと同じデータを使用して、Scikit-Learnクラスを使用してクラスタリングを実行する方法を見てみましょう。

from sklearn.cluster import DBSCAN## クラスタリングの実行dbscan_pred = DBSCAN(eps=2, min_samples=5).fit_predict(df[['total_bill','tip']])df['DBSCAN_Pred'] = dbscan_pred## クラスタリング後のデータのプロットsns.set_style('whitegrid')sns.jointplot(x='total_bill', y='tip', data=df, hue='DBSCAN_Pred',palette='coolwarm');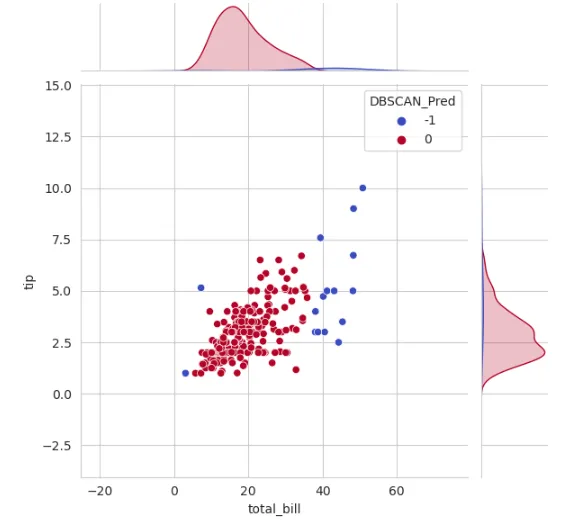

ノイズデータサンプルはラベル-1が与えられていることに注意してください。

その他のクラスタリングアルゴリズムには、凝集クラスタリング、平均シフトクラスタリング、アフィニティ伝播クラスタリング、スペクトラルクラスタリングなどがあります。

これで、クラスタリングアルゴリズムの実装方法を学びました。次に、これらのメソッドを次元削減問題にどのように使用できるかを見てみましょう。

クラスタリングを次元削減の方法として使用する

データのクラスタリングが完了したら、各インスタンスが各クラスタとの関連性を見つけることができます。

アフィニティは、各インスタンスが異なるクラスタにどれだけ適合しているかを測定する指標です。

各インスタンスのアフィニティベクトルを取得した後、元のインスタンスをそのアフィニティベクトルで置き換えることができます。アフィニティベクトルがk次元である場合、データの新しい次元はkのみになります。

元のデータがいくつの次元であっても、クラスタリング後、データの次元はデータが分割されたクラスタの数と等しくなります。

このデモンストレーションではアヤメの花のデータセットを使用しましょう。

## 必要なインポートimport numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_splitfrom sklearn.ensemble import RandomForestClassifierfrom sklearn.metrics import confusion_matrix## データセットの読み込みdf1 = pd.read_csv('データパス')## 不要な特徴量の削除df1.drop('Id',axis=1,inplace=True)## データを従属変数と独立変数に分割X = df1.drop('Species',axis=1)y = df1['Species']## データをトレーニングデータとテストデータに分割X_train, X_test, y_train, y_test = train_test_split(X, y,random_state=238, test_size=0.33)## まずは次元削減のテクニックを使用せずにモデルを直接トレーニングしましょう## ここではランダムフォレスト分類器モデルを使用しますrfc = RandomForestClassifier(n_estimators=250,n_jobs=-1,max_depth=3)rfc.fit(X_train, y_train)rfc_predictions = rfc.predict(X_test)## 予測の混同行列を確認from sklearn.metrics import confusion_matrixmatrix = confusion_matrix(y_test, rfc_predictions)print("次元削減手法を適用する前に作成されたモデルの混同行列:\n")confusion_matrix(y_test,rfc_predictions, labels = df1['Species'].unique())

## 必要なインポートfrom sklearn.cluster import KMeans## 3つのクラスタを作成しましょうk = 3kmeans = KMeans(n_clusters=k)kmeans.fit(X_train)X_train_new = kmeans.transform(X_train)## これらの値を新しいトレーニングセットとして使用するrfc_new = RandomForestClassifier(max_depth=3,n_jobs=-1,n_estimators=250)rfc_new.fit(X_train_new,y_train)rfc_new_predictions = rfc_new.predict(kmeans.transform(X_test))## インスタンスの特徴ベクトルをアフィニティベクトルで置き換えた後の予測の混同行列を確認print("インスタンスの特徴ベクトルをアフィニティベクトルで置き換えた後に作成されたモデルの混同行列:\n")confusion_matrix(y_test,rfc_new_predictions, labels = df1['Species'].unique())

ここで、以前よりも不正確な予測が2つ増えていることがわかります。これは次元削減手法が一部の情報を失っているためです。ただし、不正確な予測が2つしかないことは、高い精度を示しています。

この記事がお気に召しましたら、ぜひご意見をお聞かせください。建設的なフィードバックは大変に高く評価されます。LinkedInで私とつながってください。素晴らしい一日をお過ごしください！

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!