「時間差学習と探索の重要性：図解ガイド」

Importance of Temporal Difference Learning and Exploration Illustrated Guide

ダイナミックなグリッドワールドでのモデルフリーとモデルベースの強化学習手法の比較

最近、強化学習（RL）アルゴリズムは、タンパク質の折りたたみ、ドローンレースでの超人レベルの到達、さらにはお気に入りのチャットボットに人間のフィードバックを組み込むなど、研究問題の解決において注目を集めています。

実際に、RLはさまざまな連続的な意思決定問題に有用な解決策を提供します。Temporal-Difference Learning（TD学習）は、RLアルゴリズムの人気のあるサブセットです。TD学習方法は、環境のダイナミクスの完璧なモデルを必要とせずに学習を加速させるために、モンテカルロ法と動的プログラミング法の重要な側面を組み合わせています。

本記事では、カスタムのグリッドワールドで異なる種類のTDアルゴリズム（Q学習、Dyna-Q、Dyna-Q+）を比較します。実験の設計により、連続的な探索の重要性とテストされたアルゴリズムの個別の特性が明らかになります。

この記事の概要は以下の通りです：

• プログラム合成 – コードが自己書きすることを実現する
• PyTorchを使用して畳み込みニューラルネットワークを構築する
• 「AGENTS内部 半自律LLMエージェントを構築するための新しいオープンソースフレームワーク」

• 環境の説明
• Temporal-Difference（TD）学習
• モデルフリーのTD手法（Q学習）とモデルベースのTD手法（Dyna-QとDyna-Q+）
• パラメータ
• 性能比較
• 結論

結果とプロットを再現するための完全なコードは、こちらから入手できます：https://github.com/RPegoud/Temporal-Difference-learning

環境

この実験で使用する環境は、以下の特徴を持つグリッドワールドです：

• グリッドは12×8のセルで構成されています。
• エージェントはグリッドの左下隅からスタートし、トップ右隅にある宝物に到達することが目標です（報酬1の終端状態）。
• 青いポータルは接続されており、セル(10, 6)にあるポータルを通ることでセル(11, 0)に移動できます。エージェントは最初の移動後に再びポータルを利用することはできません。
• 紫色のポータルは100エピソード後にのみ現れますが、エージェントをより早く宝物に到達させることができます。これは環境の持続的な探索を促進します。
• 赤いポータルは罠です（報酬0の終端状態）であり、エピソードを終了させます。
• 壁にぶつかるとエージェントは同じ状態に留まります。

この実験は、Q学習、Dyna-Q、Dyna-Q+のエージェントの振る舞いを変化する環境で比較することを目的としています。実際に、100エピソード後に、最適方策は変わり、成功したエピソード中の最適なステップ数は17から12に減少します。

Temporal-Difference Learningの紹介：

Temporal-Difference Learning（一時差分学習）はモンテカルロ（MC）と動的計画法（DP）の組み合わせです：

• MC法のように、TD法は環境のダイナミクスのモデルを必要とせず、経験から学習することができます。
• DP法のように、TD法は他の学習済みの推定値に基づいて各ステップ後に推定値を更新します（これをブートストラップと呼びます）。

TD法の特徴の一つは、エピソードの終わりまで待つのではなく、各タイムステップで値の推定を更新することです。

実際、両方の方法には異なる更新ターゲットがあります。MC法はエピソードの終わりにのみ利用可能なリターンGtを更新することを目指します。一方、TD法のターゲットは次のようになります：

ここで、Vは真の価値関数Vπの推定値です。

したがって、TD法は真の値の推定値を使用することによるMC法のサンプリングと、さらなる推定に基づく推定値を用いたDP法のブートストラップを組み合わせています。

一時差分学習の最も単純なバージョンはTD(0)またはワンステップTDと呼ばれ、TD(0)の実装例は次のようになります：

状態Sから新しい状態S’への遷移時、TD(0)アルゴリズムはバックアップ値を計算し、V(S)を更新します。このバックアップ値はTD誤差と呼ばれ、最適な価値関数 V_star と現在の推定値 V(S) の差です：

結論として、TD法にはいくつかの利点があります：

• 環境のダイナミクスの完璧なモデルは必要ありません
• 各タイムステップ後にターゲットを更新するオンラインの形式で実装されています
• 固定された方策 π に対して、TD(0)は確率的近似条件に従う学習率（αまたはステップサイズ）αで収束することが保証されています（詳細については、[4]の「Tracking a Nonstationary Problem」の55ページを参照してください）

実装の詳細：

以下のセクションでは、いくつかのTDアルゴリズムの主な特徴とグリッドワールドでのパフォーマンスについて説明します。

簡単のため、全てのモデルには同じパラメータが使用されました：

• Epsilon (ε) = 0.1：ε-グリーディーポリシーでランダムなアクションを選択する確率
• Gamma (γ)= 0.9：将来の報酬または価値の推定値に適用される割引率
• Aplha (α) = 0.25：Q値の更新を制限する学習率
• Planning steps = 100：Dyna-QおよびDyna-Q+のため、直接の相互作用ごとに実行される計画ステップの数
• Kappa (κ)= 0.001：Dyna-Q+のため、計画ステップ中に適用されるボーナス報酬の重み

各アルゴリズムのパフォーマンスは、最初に400エピソードの単一の実行で示され（セクション：Q-learning、Dyna-Q、Dyna-Q+）、次に250エピソードの100回の実行で平均化されます（「summary and algorithms comparison」セクション）。

Q学習

ここで最初に実装するアルゴリズムは、有名なQ学習（Watkins, 1989）です：

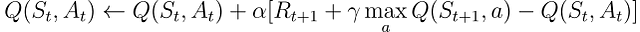
Q学習はオフポリシーアルゴリズムと呼ばれます。その目標は、エージェントが従う方策πの価値関数ではなく、直接最適な価値関数を近似することです。

実際には、Q学習は依然として方策に依存します。しばしば「行動方策」と呼ばれるものを使用して、どの状態-行動ペアを訪れて更新するかを選択します。ただし、Q学習はオフポリシーであるため、選択された行動が現在の方策πに従っているかどうかに関係なく、将来の報酬の最良の推定に基づいてQ値を更新します。

前のTD学習の疑似コードと比較すると、3つの主な違いがあります：

• すべての状態と行動のQ関数を初期化する必要があり、Q(ターミナル)は0である必要があります
• 行動は、Q値に基づいた方策から選択されます（たとえば、Q値に関してε-グリーディ方策）
• 更新対象は状態価値関数Vではなく、行動価値関数Qです

最初のアルゴリズムをテストするために、トレーニングフェーズを開始できます。エージェントは、Q値に関してε-グリーディ方策を使用してグリッドワールドをナビゲートします。この方策は、確率(1 – ε)で最も高いQ値を持つ行動を選択し、確率εでランダムな行動を選択します。各行動の後、エージェントはQ値の推定を更新します。

グリッドワールドの各セルの推定最大行動価値Q(S, a)の進化をヒートマップで視覚化することができます。ここではエージェントが400エピソードをプレイします。エピソードごとに1回の更新しかないため、Q値の進化は非常に遅く、多くの状態がマッピングされないままになります：

400エピソードの完了後、各セルへの総訪問回数の分析を行うと、エージェントの平均経路のまずまずの推定が得られます。以下の右側のプロットに示されているように、エージェントはサブオプティマルな経路に収束しているようで、セル(4,4)を避けて一貫して下の壁に沿って進んでいます。

このサブオプティマルな戦略の結果、エージェントはエピソードごとに最低21ステップに達し、”総訪問回数”プロットに示されたパスに従います。ステップ数の変動は、ε-グリーディ方策によるものであり、ランダムな行動の発生による潜在的な混乱を制限するために下の壁に従うことは合理的な戦略です。

結論として、Q学習エージェントは先述の通りサブオプティマルな戦略に収束しました。さらに、一部の環境はQ関数によって未探索のままであり、紫のポータルが100エピソード後に現れた場合に新しい最適な経路を見つけることができないようになっています。

これらのパフォーマンスの制約は、比較的少ないトレーニングステップ（400）に起因しており、環境とε-グリーディポリシーによって誘発される探索との相互作用の可能性を制限しています。

計画は、モデルベースの強化学習手法の重要な要素であり、サンプル効率と行動価値の推定の改善に特に役立ちます。Dyna-QとDyna-Q+は、計画ステップを組み込んだTDアルゴリズムの良い例です。

Dyna-Q

Dyna-Qアルゴリズム（ダイナミックQ学習）は、モデルベースのRLとTD学習の組み合わせです。

モデルベースのRLアルゴリズムは、環境のモデルを使用して計画を組み込んだ価値推定の主要な方法としています。一方、モデルフリーアルゴリズムは、直接の学習に依存しています。

「環境のモデルとは、エージェントが環境がどのように応答するかを予測するために使用できるものです」 – 強化学習：イントロダクション。

この記事の範囲では、モデルは遷移ダイナミクスp（s’、r | s、a）の近似と見なすことができます。ここで、pは現在の状態-行動ペアが与えられた場合に単一の次の状態と報酬のペアを返します。

pが確率的な環境である場合、分布モデルとサンプルモデルを区別します。前者は次の状態と行動の分布を返し、後者は推定分布からサンプリングされた単一のペアを返します。

モデルは特にエピソードをシミュレートするために役立ち、実世界の相互作用を計画ステップで置き換えることによってエージェントをトレーニングすることができます。

Dyna-Qアルゴリズムを実装するエージェントは計画エージェントのクラスに属し、直接の強化学習とモデル学習を組み合わせています。彼らは環境との直接の相互作用を使用して価値関数を更新する（Q学習と同様）だけでなく、環境のモデルを学ぶためにも使用します。各直接の相互作用の後、彼らはシミュレートされた相互作用を使用して価値関数を更新するための計画ステップも実行することができます。

クイックチェスの例

良いチェスの試合をプレイしていると想像してください。各手の後、相手の反応によって手の質を評価することができます。これはポジティブまたはネガティブな報酬を受け取ることに似ており、戦略を「更新」することができます。自分の手が大失態につながる場合、同じボードの構成が与えられた場合にはそれを再び行わないでしょう。これまでのところ、これは直接の強化学習に類似しています。

さらに、計画を追加しましょう。各手の後、相手が考えている間に、あなたは自分の前の手を振り返ってその質を再評価することができます。最初に見落とした弱点や、特定の手が思ったよりも良かったことがわかるかもしれません。これらの考えは戦略を更新することもできます。これが計画の本質です、実際の環境との相互作用ではなく、環境のモデルを使用して価値関数を更新することです。

したがって、Dyna-QはQ学習と比較していくつかの追加のステップを含んでいます：

Q値の直接の更新の後、モデルは観測された状態-行動ペアと報酬、および次の状態を保存します。このステップはモデルトレーニングと呼ばれます。

• モデルトレーニングの後、Dyna-Qはn回の計画ステップを実行します：
• モデルバッファからランダムな状態-行動ペアを選択します（つまり、この状態-行動ペアは直接の相互作用中に観測されました）
• モデルはシミュレートされた報酬と次の状態を生成します
• シミュレートされた観測（s、a、r、s’）を使用して価値関数を更新します

次に、n=100を使用してDyna-Qアルゴリズムによる学習プロセスを再現します。これは、環境との直接的な相互作用の後、モデルを使用して100回の計画ステップ（つまり、更新）を行います。

以下のヒートマップは、Dyna-Qモデルの高速収束を示しています。実際、このアルゴリズムは10エピソード程度で最適なパスを見つけることができます。これは、各ステップがQ値の101回の更新（Q学習の1回とは異なる）につながるためです。

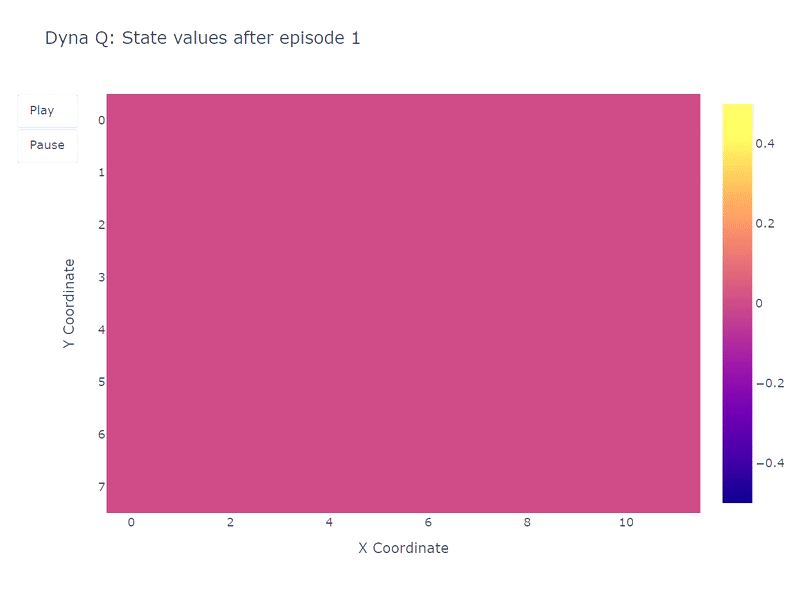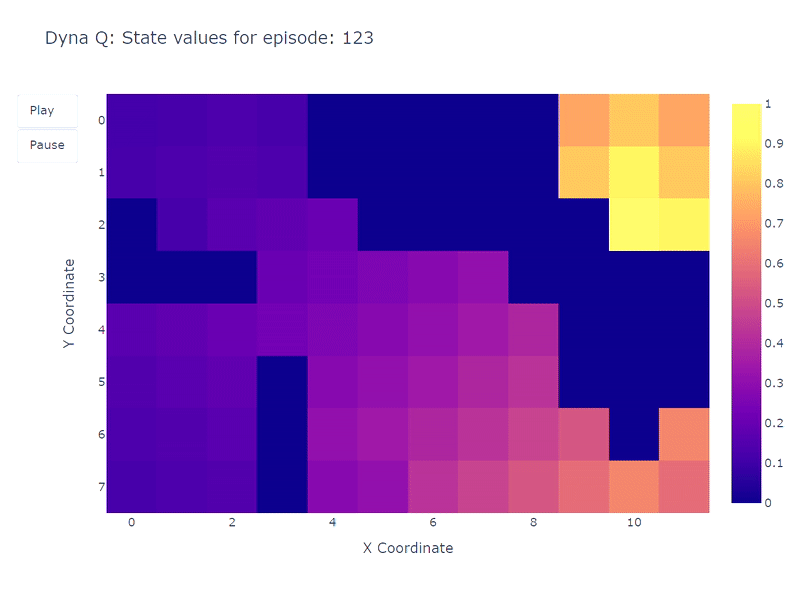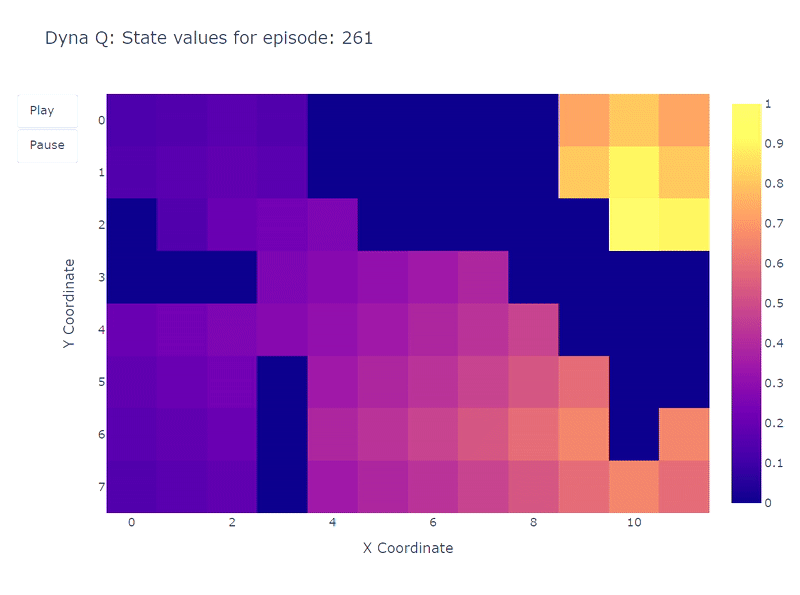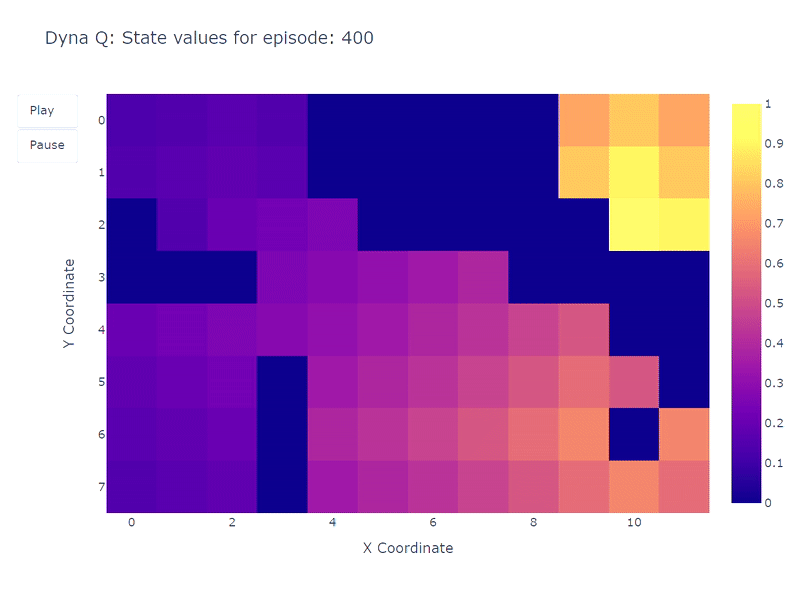
計画ステップのもう一つの利点は、グリッド全体でのアクション値のより正確な推定です。間接的な更新はモデル内に保存されたランダムな遷移をターゲットとするため、ゴールから遠い状態も更新されます。

一方で、Q学習ではアクション値がゴールから徐々に広がっていくため、グリッドの不完全なマッピングが生じます。

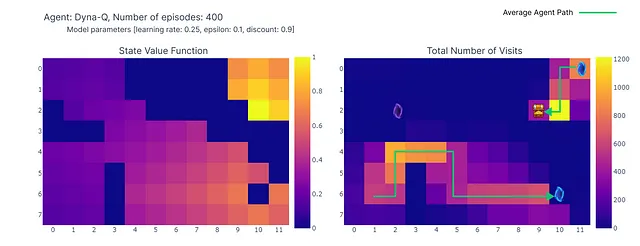
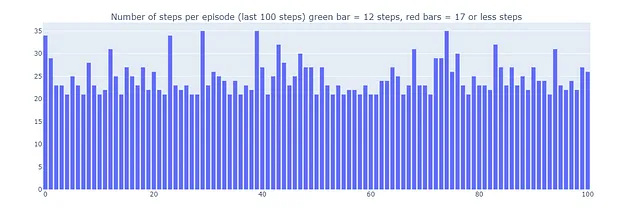
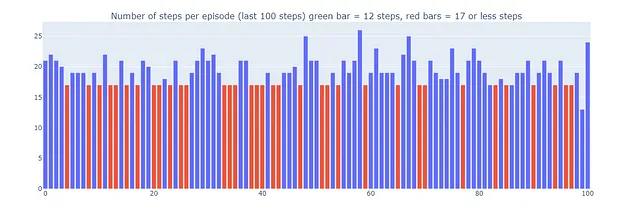
Dyna-Qを使用することで、ゴールワールドを17ステップで解決する最適なパスを見つけることができます。赤いバーで示されているプロットで、最適なパフォーマンスが定期的に達成されますが、時折探索のためにε-グリーディなアクションが干渉することもあります。

最後に、Dyna-Qは計画の組み込みによりQ学習よりも説得力があるように見えるかもしれませんが、計画は計算コストと現実世界の探索とのトレードオフを導入することを忘れないようにしてください。

Dyna-Q+

これまでにテストされたアルゴリズムのどちらも、100ステップ後に表示される最適なパス（紫のポータル）を見つけることはできませんでした。実際、両方のアルゴリズムは迅速に最適な解に収束し、トレーニングフェーズの終わりまで変わることはありませんでした。これは、トレーニング中に持続的な探索が必要であることを示しています。

Dyna-Q+はDyna-Qと非常に似ていますが、アルゴリズムに小さな変更を加えています。具体的には、Dyna-Q+は環境との実際の相互作用で試された各状態-アクションペアが試されてから経過した時間ステップ数を常に追跡します。

特に、τ時間ステップで試されていない報酬rをもたらす遷移を考えてみましょう。Dyna-Q+は、この遷移の報酬がr + κ √τであるかのように計画を実行します。ここで、κは十分に小さい値（実験では0.001）です。

この報酬設計の変更により、エージェントは環境を持続的に探索することが奨励されます。これにより、ある状態-アクションペアが試されていない時間が長ければ長いほど、そのペアのダイナミクスが変化したり、モデルが正しくない可能性が高まると仮定しています。

以下のヒートマップに示されているように、Dyna-Q+は以前のアルゴリズムと比較して、更新が非常に活発です。エピソード100までに、エージェントはグリッド全体を探索し、青いポータルと最初の最適経路を見つけます。

残りのグリッドの行動価値は、左上の状態-行動ペアが一定期間探索されないために減少し、徐々に再び増加します。

エピソード100で紫のポータルが現れると、エージェントは新しいショートカットと全体のエリアの価値を見つけます。400エピソードの完了まで、エージェントはグリッドの定期的な探索を維持しながら、各状態-行動ペアの行動価値を継続的に更新します。

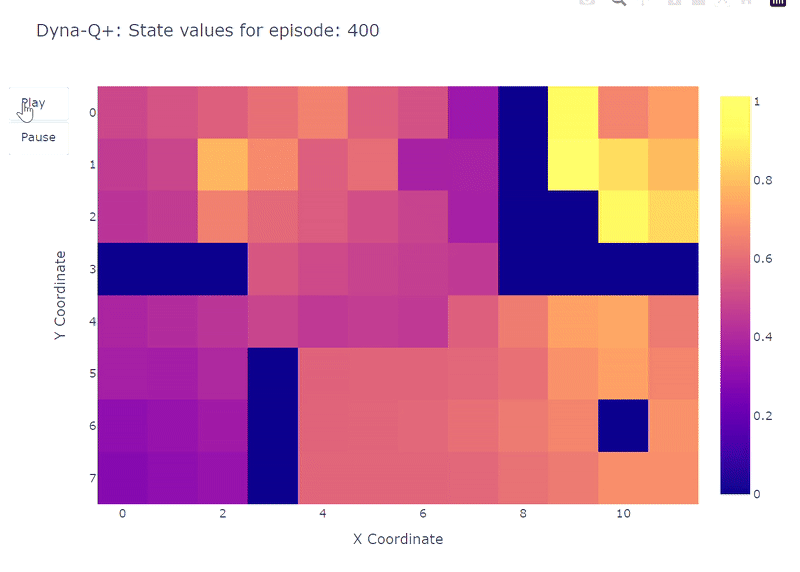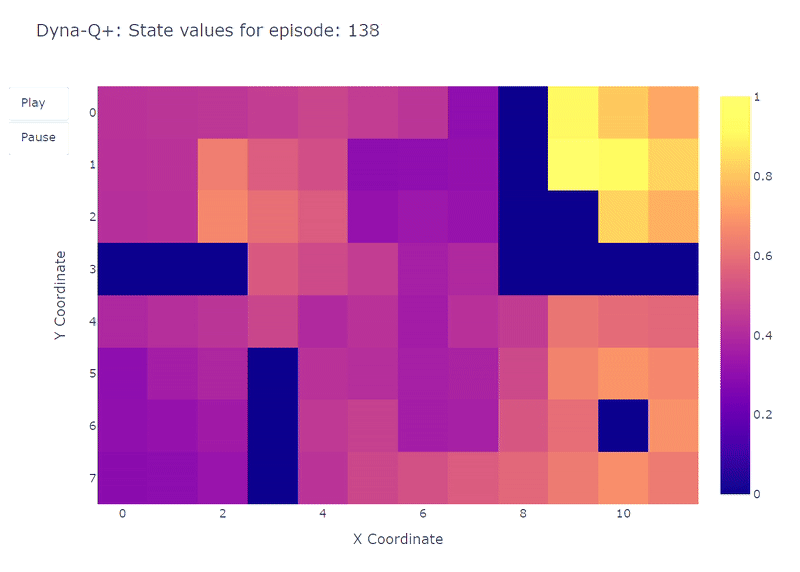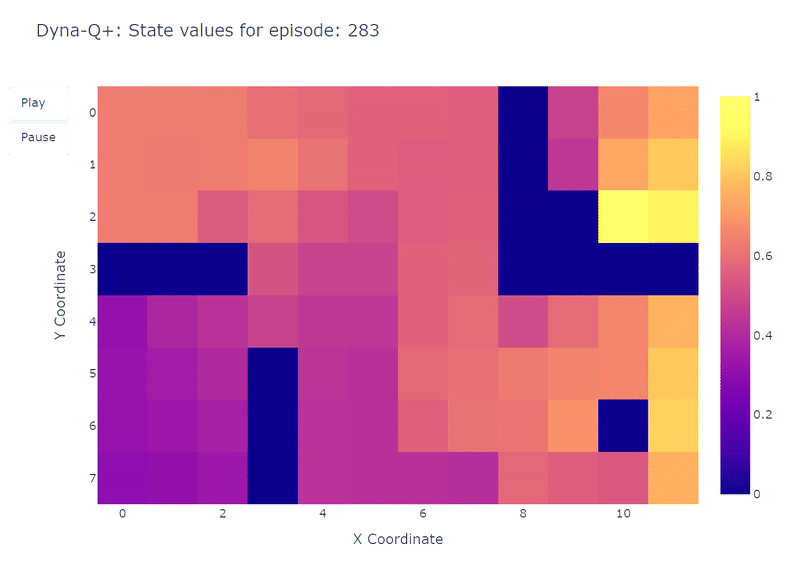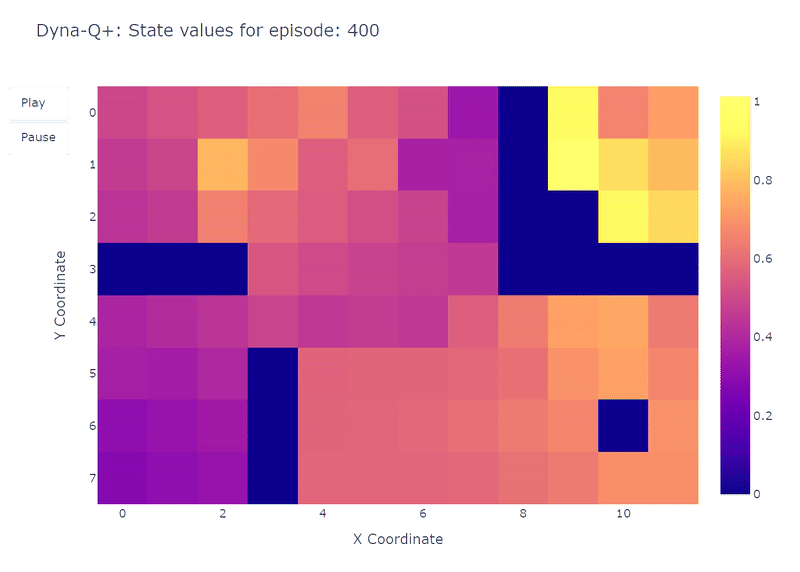
モデルの報酬に追加されたボーナスのおかげで、私たちはついにQ関数の完全なマッピング（各状態またはセルには行動価値があります）を得ます。

連続的な探索と組み合わせることで、エージェントは新しい最適経路（つまり、最適方策）を見つけ、以前の解決策を保持します。

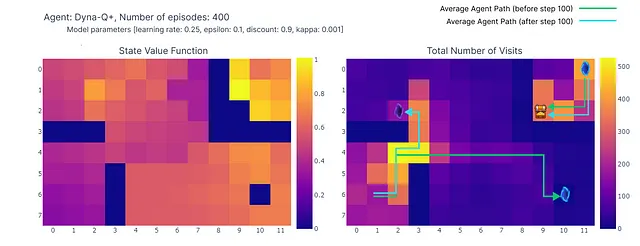
ただし、Dyna-Q+の探索と活用のトレードオフにはコストがかかります。十分な期間訪問されていない状態-行動ペアでは、探索ボーナスがエージェントを再訪させることが奨励され、その結果として一時的なパフォーマンスの低下が生じることがあります。この探索の挙動は、長期的な意思決定の改善のためにモデルの更新を優先します。

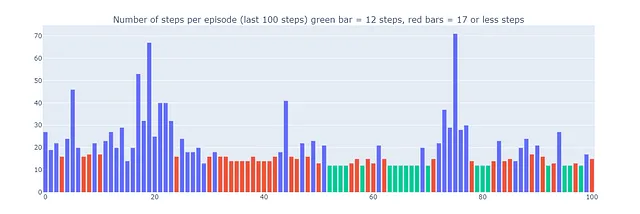
これにより、Dyna-Q+によって再生されるエピソードは、最大で70ステップになる場合があります。これに対して、Q学習とDyna-Qはそれぞれ最大で35ステップと25ステップです。Dyna-Q+の長いエピソードは、環境についてのより多くの情報を収集し、モデルを改善するために探索に追加のステップを投資する意思を持つエージェントを反映しています。

一方、Dyna-Q+は以前のアルゴリズムが達成しなかった最適なパフォーマンス（プロット下の緑の棒で示されています）を定期的に達成します。

まとめとアルゴリズムの比較

アルゴリズム間の主な違いを比較するために、2つのメトリックを使用します（単純化のために、すべてのモデルの入力パラメータは同一であることに注意してください）：

• エピソードごとのステップ数：このメトリックは、アルゴリズムが最適解に収束する速度を特徴付けます。また、収束後のアルゴリズムの挙動、特に探索に関しても説明します。
• 平均累積報酬：正の報酬に至るエピソードの割合

エピソードごとのステップ数を分析すると（下のプロットを参照）、モデルベースとモデルフリーのメソッドのいくつかの側面が明らかになります：

• モデルベースの効率性：モデルベースのアルゴリズム（Dyna-QとDyna-Q+）は、この特定のグリッドワールドではサンプル効率が高い傾向があります（これはRL全般でも観察される特性です）。これは、環境の学習済みモデルを使用して先を見越すことができるため、近似最適または最適解により迅速に収束することができるためです。
• Q学習の収束：Q学習は最終的に近似最適解に収束しますが、そのためにはより多くのエピソード（125）が必要です。Q学習はステップごとに1回の更新のみを行うため、Dyna-QとDyna-Q+が複数回の更新を行うのとは対照的です。
• 複数回の更新：Dyna-QとDyna-Q+はステップごとに101回の更新を行いますが、これはより速い収束に貢献します。ただし、このサンプル効率のためのトレードオフは、計算コストです（テーブルのランタイムセクションを参照）。
• 複雑な環境：より複雑または確率的な環境では、モデルベースの手法の利点は減少する場合があります。モデルは誤差や不正確さを導入する可能性があり、最適方策につながらない場合があります。したがって、この比較は、異なるアプローチの強みと弱みの概要として見るべきであり、直接的なパフォーマンス比較ではありません。

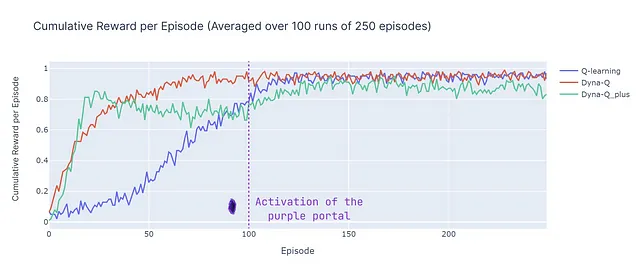
ここでは、平均累積報酬（ACR）を紹介します。これは、エージェントがゴールに到達するエピソードの割合を表しています（ゴールに到達した場合の報酬が1で、トラップを引き起こした場合の報酬が0です）。ACRは次のように単純に計算されます：

Nはエピソード数（250）、Kは独立した実行回数（100）、Rn,kは実行kのエピソードnの累積報酬です。

以下はすべてのアルゴリズムのパフォーマンスの詳細です：

• Dyna-Qは迅速に収束し、最も高い全体の報酬（ACR 87%）を達成します。つまり、効率的に学習し、多くのエピソードでゴールに到達します。
• Q-learningも同様のパフォーマンスレベルに達しますが、収束するためにより多くのエピソードが必要であり、そのためACRはわずか70%です。
• Dyna-Q+はわずか15エピソード後に累積報酬0.8を達成し、すぐに良い方策を見つけます。しかし、ボーナス報酬によって引き起こされる変動性と探索は、100ステップまで性能を低下させます。100ステップ後、新しい最適なパスを発見することで改善が始まります。ただし、短期的な探索はパフォーマンスを損ない、ACRはDyna-Qより低いがQ-learningより高い79%になります。

結論

この記事では、時系列差分学習の基本原理を紹介し、Q-learning、Dyna-Q、およびDyna-Q+をカスタムのグリッドワールドに適用しました。このグリッドワールドの設計は、変化する環境で新しい最適方策を発見して利用するための継続的な探索の重要性を強調しています。ステップ数ごとのエピソード数と累積報酬によるパフォーマンスの違いは、これらのアルゴリズムの強みと弱点を示しています。

要約すると、モデルベースの手法（Dyna-Q、Dyna-Q+）は、モデルベースの手法（Q-learning）に比べてサンプル効率が向上していますが、計算効率は低下しています。しかし、確率的またはより複雑な環境では、モデルの不正確さがパフォーマンスを妨げ、サブオプティマルな方策につながる可能性があります。

参考文献:

[1] Demis Hassabis, AlphaFold reveals the structure of the protein universe (2022), DeepMind

[2] Elia Kaufmann, Leonard Bauersfeld, Antonio Loquercio, Matthias Müller, Vladlen Koltun &Davide Scaramuzza, Champion-level drone racing using deep reinforcement learning (2023), Nature

[3] Nathan Lambert, LouisCastricato, Leandro von Werra, Alex Havrilla, Illustrating Reinforcement Learning from Human Feedback (RLHF), HuggingFace

[4] Sutton, R. S., & Barto, A. G. . Reinforcement Learning: An Introduction (2018), Cambridge (Mass.): The MIT Press.

[5] Christopher J. C. H. Watkins & Peter Dayan, Q-learning (1992), Machine Learning, Springer Link

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!