グループ化および空間計量データの混合効果機械学習におけるGPBoost

GPBoost in Machine Learning with Mixed Effects of Grouping and Spatial Metric Data.

欧州GDPデータを用いたデモ

Spatial effect (after factoring out the predictor variables) and effect of predictor variable ‘K’ on European GDP — Image by Author — 空間効果(予測変数を除いた後)および予測変数「K」の欧州GDPへの影響 — オーサーの画像

∘ はじめに · データの説明 · データの読み込みと簡単な可視化 ∘ GPBoostモデルのトレーニング ∘ チューニングパラメータの選択 ∘ モデルの解釈 · 推定されたランダム効果モデル · 空間効果マップ · 固定効果関数の理解 ∘ 拡張 · 異なる時期のための別々のランダム効果 · 空間と固定効果予測変数の相互作用 · 大量データ · 他の空間ランダム効果モデル · (一般化)線形混合効果とガウス過程モデル ∘ 参考文献

はじめに

GPBoostアルゴリズムは、線形混合効果とガウス過程モデルを拡張し、ツリーブースティングを用いた非パラメトリックな非線形関数によって線形固定効果関数を置き換えることで、空間的およびグループ構造を持つデータのモデリングに使用できます。本記事では、GPBoostライブラリに実装されたGPBoostアルゴリズムの機能を、地域的空間計量データの例である欧州GDPデータを用いて示します。すべての結果は、GPBoostのバージョン1.2.1を使用しています。このデモはRパッケージを使用していますが、対応するPythonパッケージも同様の機能を提供しています。

GPBoostモデル（= ツリーブースティングとランダム効果/GPモデルの組み合わせ）を適用するには、次の主要なステップが必要です。

ランダム効果モデル（例えば、空間ランダム効果、グループランダム効果、空間とグループを組み合わせたものなど）
応答変数と固定効果予測変数を含むgpb.Datasetを作成する
関数gpb.grid.search.tune.parametersを使用して、チューニングパラメータを選択する
gpboost/gpb.train関数を使用してモデルをトレーニングする

本記事では、実世界のデータセットを使用してこれらのステップを実証し、適合したモデルの解釈方法を示し、GPBoostライブラリのいくつかの拡張と追加機能を見ていきます。

データの説明

このデモで使用されるデータは、欧州の国内総生産（GDP）データです。https://raw.githubusercontent.com/fabsig/GPBoost/master/data/gdp_european_regions.csvからダウンロードできます。データは、Massimo Giannini氏（ローマ・トーリベルガータ大学）によってEurostatから収集され、2023年6月16日にローマ・トーリベルガータ大学での講演のためにFabio Sigrist氏に親切に提供されました。

242の欧州地域のデータが、2000年と2021年の2年間で収集されました。つまり、データポイントの総数は484です。応答変数は（対数）GDP/人口あたりです。予測変数は4つあります:

L: （対数）雇用割合（empl/pop）
K: （対数）固定資本/人口
Pop: 対数（人口）
Edu: 第三次教育の割合

さらに、各地域の重心空間座標（経度と緯度）、242の異なる欧州地域の空間領域ID、および地域が属するクラスタを識別する追加の空間クラスタIDがあります（2つのクラスタがあります）。

データの読み込みと簡単な可視化

まず、データを読み込み、空間上の（対数）GDP/人口あたりを示す地図を作成します。

library(gpboost)data <- read.csv("https://raw.githubusercontent.com/fabsig/GPBoost/master/data/gdp_european_regions.csv")data <- as.matrix(data) # convert to matrix since the boosting part currently does not support data.framescovars <- c("L", "K", "pop", "edu")library(ggplot2)library(viridis)library(gridExtra)p1 <- ggplot(data = data.frame(Lat=data[,"Lat"], Long=data[,"Long"],                               GDP=data[,"y"]), aes(x=Long,y=Lat,color=GDP)) +  geom_point(size=2, alpha=0.5) + scale_color_viridis(option = "B") +   ggtitle("GDP / capita (log)")p2 <- ggplot(data = data.frame(Lat=data[,"Lat"], Long=data[,"Long"],                                GDP=data[,"y"]), aes(x=Long,y=Lat,color=GDP)) +  geom_point(size=3, alpha=0.5) + scale_color_viridis(option = "B") +   ggtitle("GDP / capita (log) -- Europe excluding islands") + xlim(-10,28) + ylim(35,67)grid.arrange(p1, p2, ncol=2)

242 European regionsのlog GDP / capita — Image by Author

GPBoostモデルのトレーニング

以下では、指数カバリアンス関数を持つガウシアンプロセスモデルを使用して、空間ランダム効果をモデル化します。さらに、クラスタ変数clのグループ化されたランダム効果も含めます。 GPBoostライブラリでは、ガウス過程ランダム効果はgp_coords引数、グループ化されたランダム効果はGPModelコンストラクタのgroup_data引数で定義されます。上記の予測変数は、固定効果ツリーアンサンブル関数に使用されます。モデルは、gpboost、または同等のgpb.train関数を使用して適合させます。クロスバリデーションを使用して選択されたチューニングパラメータを使用することに注意してください。

gp_model <- GPModel(group_data = data[, c("cl")],                     gp_coords = data[, c("Long", "Lat")],                    likelihood = "gaussian", cov_function = "exponential")params <- list(learning_rate = 0.01, max_depth = 2, num_leaves = 2^10,               min_data_in_leaf = 10, lambda_l2 = 0)nrounds <- 37# gp_model$set_optim_params(params = list(trace=TRUE)) # ハイパーパラメータ推定を監視するために使用boost_data <- gpb.Dataset(data = data[, covars], label = data[, "y"])gpboost_model <- gpboost(data = boost_data, gp_model = gp_model,                          nrounds = nrounds, params = params,                          verbose = 1) # 同じくgpb.train# 同じくgpb.train gpb.train

チューニングパラメータの選択

ブースティングに適切に選択されたチューニングパラメータが重要です。普遍的なデフォルト値はなく、すべてのデータセットで異なるチューニングパラメータが必要になる場合があります。以下のような固定グリッドサーチの代わりに、ランダムグリッドサーチを行うこともできます（num_try_randomを参照）。以下では、gpb.grid.search.tune.parameters関数を使用してチューニングパラメータを選択する方法を示します。検証データに対する平均二乗誤差（mse）を予測精度尺度として使用します。代替的に、予測の不確実性も考慮に入れることができる、例えば、テストの負の対数尤度（test_neg_log_likelihood =何も指定されていない場合のデフォルト値）を使用することもできます。

gp_model <- GPModel(group_data = data[, "cl"],                     gp_coords = data[, c("Long", "Lat")],                    likelihood = "gaussian", cov_function = "exponential")boost_data <- gpb.Dataset(data = data[, covars], label = data[, "y"])param_grid = list("learning_rate" = c(1,0.1,0.01),                   "min_data_in_leaf" = c(10,100,1000),                  "max_depth" = c(1,2,3,5,10),                  "lambda_l2" = c(0,1,10))other_params <- list(num_leaves = 2^10)set.seed(1)opt_params <- gpb.grid.search.tune.parameters(param_grid = param_grid, params = other_params,                                              num_try_random = NULL, nfold = 4,                                              data = boost_data, gp_model = gp_model,                                               nrounds = 1000, early_stopping_rounds = 10,                                              verbose_eval = 1, metric = "mse") # metric = "test_neg_log_likelihood"opt_params# ***** New best test score (l2 = 0.0255393919591794) found for the following parameter combination: learning_rate: 0.01, min_data_in_leaf: 10, max_depth: 2, lambda_l2: 0, nrounds: 37

モデルの解釈

推定されたランダム効果モデル

推定されたランダム効果モデルの情報は、gp_modelに対してsummary関数を呼び出すことで取得できます。ガウス過程の場合、GP_varはマージナル分散であり、空間相関または空間変動の量であり、GP_rangeはスケールパラメータであり、相関が空間的にどの程度速く減衰するかを測定します。指数カバリアンス関数の場合、この値の3倍（約17）は、（残差）空間相関が本質的にゼロになる距離です（5％未満）。以下の結果からわかるように、空間相関の量は比較的小さいです。なぜなら、マージナル分散が0.0089であり、応答変数の総分散（約0.29）に比べて小さいからです。また、誤差項とクラスタグループ化されたランダム効果の分散も小さい（0.013と0.022）。したがって、応答変数のほとんどの分散は、固定効果予測変数によって説明されます。

summary(gp_model)

## =====================================================## Covariance parameters (random effects):##            Param.## Error_term 0.0131## Group_1    0.0221## GP_var     0.0089## GP_range   5.7502## =====================================================

空間効果マップ

トレーニングデータの場所で推定された（「予測された」）空間ランダム効果をプロットすることができます。トレーニングデータでpredict関数を呼び出すことで、下記のコードを参照してください。このようなプロットは、固定効果予測変数の効果を除外した場合の空間効果を示します。これらの空間効果は、空間ガウス過程とグループ化された領域クラスターのランダム効果の両方を考慮しています。ガウス過程部分からのみ空間ランダム効果のみを取得したい場合は、predict_training_data_random_effects関数を使用できます（以下のコメント付きコードを参照）。また、空間外挿（「Krigging」）を行うこともできますが、面積データではあまり意味がありません。

pred <- predict(gpboost_model, group_data_pred = data[1:242, c("cl")],                 gp_coords_pred = data[1:242, c("Long", "Lat")],                data = data[1:242, covars], predict_var = TRUE, pred_latent = TRUE)plot_mu <- ggplot(data = data.frame(Lat=data[,"Lat"], Long=data[,"Long"], spat_eff=pred$random_effect_mean),aes(x=Long,y=Lat,color=spat_eff)) +  geom_point(size=3, alpha=0.5) + scale_color_viridis(option = "B") +   ggtitle("Spatial effect (mean)") + xlim(-10,28) + ylim(35,67)plot_sd <- ggplot(data = data.frame(Lat=data[,"Lat"], Long=data[,"Long"], std_dev=pred$random_effect_cov),aes(x=Long,y=Lat,color=std_dev)) +  geom_point(size=3, alpha=0.5) + scale_color_viridis(option = "B") +   ggtitle("Uncertainty (std. dev.)") + xlim(-10,28) + ylim(35,67)grid.arrange(plot_mu, plot_sd, ncol=2)# # Only spatial effecst from the Gaussian process# rand_effs <- predict_training_data_random_effects(gp_model, predict_var = TRUE)[1:242, c("GP", "GP_var")]# plot_mu <- ggplot(data = data.frame(Lat=data[,"Lat"], Long=data[,"Long"], spat_eff=rand_effs[,1]),aes(x=Long,y=Lat,color=spat_eff)) +#   geom_point(size=3, alpha=0.5) + scale_color_viridis(option = "B") + #   ggtitle("Spatial effect from Gausian process (mean)") + xlim(-10,28) + ylim(35,67)# plot_sd <- ggplot(data = data.frame(Lat=data[,"Lat"], Long=data[,"Long"], std_dev=rand_effs[,2]),aes(x=Long,y=Lat,color=std_dev)) +#   geom_point(size=3, alpha=0.5) + scale_color_viridis(option = "B") + #   ggtitle("Uncertainty (std. dev.)") + xlim(-10,28) + ylim(35,67)# grid.arrange(plot_mu, plot_sd, ncol=2)

Spatial effect (after factoring out the predictor variables) — Image by Author — 空間効果図（予測変数を除外した後）— 著者によるイメージ

固定効果関数の理解

固定効果関数の形を理解するためのいくつかのツールがあります。以下では、変数重要度測定、相互作用測定、および依存プロットを考慮します。具体的には、以下を見ます

SHAP値
SHAP依存プロット
分割ベースの変数重要度
FriedmanのH統計量
部分依存プロット（1次元および2次元）

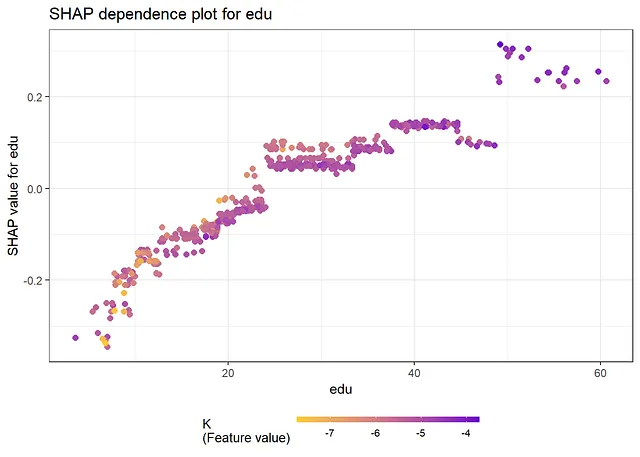
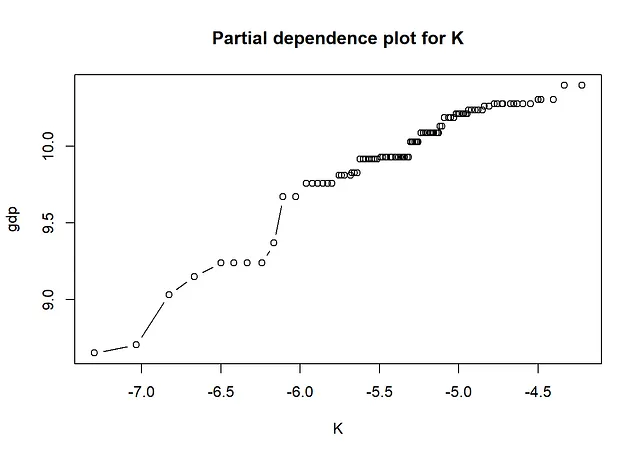
以下の結果から、SHAP値とSHAP依存プロットから得られる情報は、従来の変数重要度測定と部分依存プロットを見る場合と同じです。最も重要な変数は「K」と「edu」です。依存プロットからは、非線形性があることがわかります。たとえば、Kの効果は、Kの大きな値と小さな値ではほぼフラットで、その間では増加します。さらに、eduの効果は、eduの小さな値では急激になり、eduの大きな値では平坦になります。FriedmanのH統計量は、相互作用があることを示しています。相互作用が最も多い2つの変数、Lとpopについて、2次元部分依存プロットを以下に作成します。

# SHAP値
library(SHAPforxgboost)
shap.plot.summary.wrap1(gpboost_model, X=data[,covars]) + ggtitle("SHAP値")

# SHAP依存プロット
shap_long <- shap.prep(gpboost_model, X_train=data[,covars])
shap.plot.dependence(data_long=shap_long, x=covars[2], color_feature=covars[4], smooth=FALSE, size=2) + ggtitle("KのSHAP依存プロット")
shap.plot.dependence(data_long=shap_long, x=covars[4], color_feature=covars[2], smooth=FALSE, size=2) + ggtitle("eduのSHAP依存プロット")

# 分割ベースの特徴量重要度
feature_importances <- gpb.importance(gpboost_model, percentage=TRUE)
gpb.plot.importance(feature_importances, top_n=25, measure="Gain", main="分割ベースの変数重要度")

# 交互作用のH統計量。max_depth=1の場合、交互作用はないことに注意
library(flashlight)
fl <- flashlight(model=gpboost_model, data=data.frame(y=data[,"y"], data[,covars]), y="y", label="gpb", predict_fun=function(m, X) predict(m, data.matrix(X[,covars]), gp_coords_pred=matrix(-100, ncol=2, nrow=dim(X)[1]), group_data_pred=matrix(-1, ncol=1, nrow=dim(X)[1]), pred_latent=TRUE)$fixed_effect)
plot(imp <- light_interaction(fl, v=covars, pairwise=TRUE)) + ggtitle("H統計量の交互作用") # 数秒かかる

# 部分依存プロット
gpb.plot.partial.dependence(gpboost_model, data[,covars], variable=2, xlab=covars[2], ylab="gdp", main="Kの部分依存プロット")
gpb.plot.partial.dependence(gpboost_model, data[,covars], variable=4, xlab=covars[4], ylab="gdp", main="eduの部分依存プロット")

# 2次元偏関数プロット（相互作用を可視化するため）i = 1; j = 3;# i vs jgpb.plot.part.dep.interact(gpboost_model, data[,covars], variables = c(i,j), xlab = covars[i],                            ylab = covars[j], main = "2変数の偏関数プロット")

拡張機能

異なる時間期間の分離されたランダム効果

上記のモデルでは、2000年と2021年の両方のランダム効果に同じものを使用しました。代わりに、異なる時間期間の独立した空間およびグループ化されたランダム効果を使用することもできます（事前分布において独立であり、データに条件付けられている場合、依存関係がある…）。GPBoostライブラリでは、cluster_ids引数を使用してこれを行うことができます。cluster_idsはサンプルサイズの長さのベクトルである必要があり、各エントリは観測値が属する「クラスター」を示します。異なるクラスターは独立した空間およびグループ化されたランダム効果を有しますが、ハイパーパラメーター（例：周辺分散、分散成分など）および固定効果関数はクラスター間で同じです。

以下では、このようなモデルを適合させ、2つの分離された空間マップを作成する方法を示します。以下の結果から、2年間の空間効果はかなり異なります。特に、2021年には2000年に比べて空間変動（または異質性）が少なくなっています。これは、予測された空間ランダム効果の標準偏差を見ることによって確認されます。2000年の場合、空間効果の標準偏差が2021年のほぼ2倍であることがわかります（以下参照）。さらに、2000年には「低い」GDP数値（0以下の空間効果）の地域がより多かったことがわかります。しかし、2021年にはそのような地域は存在しません。

gp_model <- GPModel(group_data = data[, c("cl")], gp_coords = data[, c("Long", "Lat")],                    likelihood = "gaussian", cov_function = "exponential",                    cluster_ids  = c(rep(1,242), rep(2,242)))boost_data <- gpb.Dataset(data = data[, covars], label = data[, "y"])params <- list(learning_rate = 0.01, max_depth = 1, num_leaves = 2^10,               min_data_in_leaf = 10, lambda_l2 = 1) # 注：上記と同じチューニングパラメーターを使用します。理想的には、再度選択する必要がありますgpboost_model <- gpboost(data = boost_data, gp_model = gp_model, nrounds = nrounds,                         params = params, verbose = 0)# 2000年と2021年の分離された空間マップpred <- predict(gpboost_model, group_data_pred = data[, c("cl")],                 gp_coords_pred = data[, c("Long", "Lat")],                data = data[, covars], predict_var = TRUE, pred_latent = TRUE,                cluster_ids_pred = c(rep(1,242), rep(2,242)))plot_mu_2000 <- ggplot(data = data.frame(Lat=data[,"Lat"], Long=data[,"Long"],                                          spat_eff=pred$random_effect_mean[1:242]),                        aes(x=Long,y=Lat,color=spat_eff)) +  geom_point(size=3, alpha=0.5) + scale_color_viridis(option = "B") +   ggtitle("2000年の空間効果（平均）") + xlim(-10,28) + ylim(35,67)plot_mu_2021 <- ggplot(data = data.frame(Lat=data[,"Lat"], Long=data[,"Long"],                                          spat_eff=pred$random_effect_mean[243:484]),                        aes(x=Long,y=Lat,color=spat_eff)) +  geom_point(size=3, alpha=0.5) + scale_color_viridis(option = "B") +   ggtitle("2021年の空間効果（平均）") + xlim(-10,28) + ylim(35,67)grid.arrange(plot_mu_2000, plot_mu_2021, ncol=2)

空間効果と固定効果予測変数の相互作用

上記のモデルでは、ランダム効果と固定効果予測変数の間には相互作用はありません。つまり、空間座標と固定効果予測変数の間には相互作用がありません。このような相互作用は、ランダム効果入力変数（=空間座標またはカテゴリー分類変数）を固定効果関数に追加することでモデル化することができます。以下のコードは、これを行う方法を示しています。下の変数重要度プロットに示すように、座標はツリーアンサンブルで使用されず、このデータセットではそのような相互作用は検出されません。

gp_model <- GPModel(group_data = data[, c("cl")], gp_coords = data[, c("Long", "Lat")],                    likelihood = "gaussian", cov_function = "exponential")covars_interact <- c(c("Long", "Lat"), covars) ## 固定効果予測変数に空間座標を追加するboost_data <- gpb.Dataset(data = data[, covars_interact], label = data[, "y"])params <- list(learning_rate = 0.01, max_depth = 1, num_leaves = 2^10,               min_data_in_leaf = 10, lambda_l2 = 1) # 注意：上記と同じチューニングパラメータを使用しています。理想的には、再度選択する必要がありますgpboost_model <- gpboost(data = boost_data, gp_model = gp_model, nrounds = nrounds,                         params = params, verbose = 0)feature_importances <- gpb.importance(gpboost_model, percentage = TRUE)gpb.plot.importance(feature_importances, top_n = 25, measure = "Gain",                     main = "座標を固定効果に含めた場合の変数の重要度")

大規模データ

大規模データセットでは、ガウス過程による計算は遅くなり、近似値を使用する必要があります。GPBoost ライブラリには、いくつかの近似値が実装されています。たとえば、GPModel コンストラクタで gp_approx="vecchia" を設定すると、Vecchia 近似が使用されます。この記事で使用されるデータセットは比較的小さいため、すべての計算を正確に行うことができます。

その他の空間ランダム効果モデル

上記では、空間ランダム効果をモデル化するためにガウス過程を使用しました。データが面積データであるため、CARモデルやSARモデルなどのネイバーフッド情報に依存するモデルを使用することもできます。GPBoost ライブラリにはこれらのモデルが実装されていません（将来追加される可能性があります -> 著者に問い合わせてください）。

別のオプションは、空間効果をモデル化するためにカテゴリー地域ID変数で定義されるグループ化されたランダム効果モデルを使用することです。以下のコードは、GPBoost でこれを行う方法を示しています。ただし、このモデルは基本的に空間構造を無視します。

gp_model <- GPModel(group_data = data[, c("group", "cl")], likelihood = "gaussian")

(一般化)線形混合効果およびガウス過程モデル

(一般化)線形混合効果およびガウス過程モデルも、GPBoost ライブラリで実行できます。以下のコードは、fitGPModel 関数を使用してこれを行う方法を示しています。注意：切片を含めるには1の列を手動で追加する必要があります。

X_incl_1 = cbind(Intercept = rep(1,dim(data)[1]), data[, covars])gp_model <- fitGPModel(group_data = data[, c("cl")], gp_coords = data[, c("Long", "Lat")],                       likelihood = "gaussian", cov_function = "exponential",                       y = data[, "y"], X = X_incl_1, params = list(std_dev=TRUE))summary(gp_model)

## =====================================================## モデルの要約：## Log-lik     AIC     BIC ##  195.97 -373.94 -336.30 ## 観測数: 484## グループ数: 2 (Group_1)## -----------------------------------------------------## 共分散パラメータ（ランダム効果）：##            Param. Std. dev.## Error_term 0.0215    0.0017## Group_1    0.0003    0.0008## GP_var     0.0126    0.0047## GP_range   7.2823    3.6585## -----------------------------------------------------## 線形回帰係数（固定効果）：##            Param. Std. dev. z value P(>|z|)## Intercept 16.2816    0.4559 35.7128  0.0000## L          0.4243    0.0565  7.5042  0.0000## K          0.6493    0.0212 30.6755  0.0000## pop        0.0134    0.0097  1.3812  0.1672## edu        0.0100    0.0009 10.9645  0.0000## =====================================================

参考文献

Sigrist Fabio. ” Gaussian Process Boosting “. Journal of Machine Learning Research (2022).
Sigrist Fabio. ” Latent Gaussian Model Boosting “. IEEE Transactions on Pattern Analysis and Machine Intelligence (2023).
https://github.com/fabsig/GPBoost
データセットのソースはEurostatであり、権利に関する詳細についてはhttps://ec.europa.eu/eurostat/about-us/policies/copyrightを参照してください（「Eurostatは、商業利用と非商業利用の両方において、データの自由な再利用を奨励する方針を持っています。」）

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!

EconometricsMachine learningMixed EffectsRandom EffectsSpatial Analysis

Was this article helpful?

93 out of 132 found this helpful