グラフ畳み込みネットワーク:GNNの紹介
GNNの紹介
PyTorch Geometricを使用したステップバイステップガイド

Graph Neural Networks(GNN)は、ディープラーニングの領域で最も魅力的で急速に進化しているアーキテクチャの一つです。グラフ構造のデータを処理するために設計されたディープラーニングモデルとして、GNNは驚異的な柔軟性と強力な学習能力を持ちます。
さまざまなタイプのGNNの中でも、Graph Convolutional Networks(GCN)が最も普及していて広く適用されているモデルとして浮上しています。GCNは、ノードの特徴とその近傍の両方を活用して予測を行う能力を持つため、グラフ構造のデータを扱うための効果的な方法を提供します。
この記事では、GCNレイヤーのメカニズムについて詳しく説明し、その内部動作を解説します。さらに、PyTorch Geometricをツールとして使用して、ノード分類タスクへの実際の応用についても探求します。
PyTorch Geometricは、GNNの開発と実装に特化したPyTorchの拡張機能です。高度で使いやすいライブラリであり、グラフベースの機械学習を容易にするための包括的なツールセットを提供します。旅を始めるためには、PyTorch Geometricのインストールが必要です。Google Colabを使用している場合、すでにPyTorchがインストールされているはずなので、いくつかの追加のコマンドを実行するだけです。
- AWS vs Azure:究極のクラウド対決
- 「バイアス調整の力を明らかにする:不均衡なデータセットにおける予測精度の向上」
- このAI研究は、パーソン再識別に適したデータ拡張手法であるStrip-Cutmixを提案しています
すべてのコードは、Google ColabとGitHubで利用できます。
!pip install torch_geometric
import torchimport numpy as npimport networkx as nximport matplotlib.pyplot as pltPyTorch Geometricがインストールされたので、このチュートリアルで使用するデータセットを探索しましょう。
🌐 I. グラフデータ
グラフは、オブジェクト間の関係を表現するための重要な構造です。ソーシャルネットワークやコンピュータネットワーク、分子の化学構造、自然言語処理、画像認識など、さまざまな現実世界のシナリオでグラフデータに遭遇することがあります。
この記事では、悪名高くよく使用されるザカリーのカラテクラブのデータセットを研究します。

ザカリーのカラテクラブのデータセットは、1970年代にウェイン・W・ザカリーが観察したカラテクラブ内で形成される関係を具現化しています。これはソーシャルネットワークの一種であり、各ノードはクラブのメンバーを表し、ノード間のエッジはクラブの外で発生した相互作用を表します。
この特定のシナリオでは、クラブのメンバーは4つの異なるグループに分割されています。私たちのタスクは、メンバーのパターンに基づいて(ノード分類)、各メンバーに正しいグループを割り当てることです。
PyGの組み込み関数を使用してデータセットをインポートし、使用されるDatasetsオブジェクトについて理解しましょう。
from torch_geometric.datasets import KarateClub
# PyTorch Geometricからデータセットをインポートdataset = KarateClub()# 情報を表示print(dataset)print('------------')print(f'グラフの数: {len(dataset)}')print(f'特徴の数: {dataset.num_features}')print(f'クラスの数: {dataset.num_classes}')
KarateClub()------------グラフの数: 1特徴の数: 34クラスの数: 4このデータセットには1つのグラフしかありません。各ノードは34次元の特徴ベクトルを持ち、4つのクラス(4つのグループ)のいずれかに属しています。実際には、DatasetsオブジェクトはData(グラフ)オブジェクトのコレクションと見なすことができます。
ユニークなグラフをさらに調査して、詳細を把握できます。
# 最初の要素を表示print(f'グラフ: {dataset[0]}')
Graph: Data(x=[34, 34], edge_index=[2, 156], y=[34], train_mask=[34])Dataオブジェクトは特に興味深いです。表示すると、研究しているグラフの良い概要が得られます:
x=[34, 34]はノードの特徴行列で、形状は(ノードの数、特徴の数)です。この場合、34個のノード(34人のメンバー)があり、各ノードは34次元の特徴ベクトルに関連付けられています。edge_index=[2, 156]は、グラフの接続性(ノードの接続方法)を表しており、形状は(2、有向エッジの数)です。y=[34]はノードの正解ラベルです。この問題では、各ノードが1つのクラス(グループ)に割り当てられているため、各ノードに対して1つの値があります。train_mask=[34]は、TrueまたはFalseのステートメントのリストで、トレーニングに使用するノードを示すオプションの属性です。
これらのテンソルの内容を理解するために、それぞれを出力してみましょう。まず、ノードの特徴から始めましょう。
data = dataset[0]
print(f'x = {data.x.shape}')print(data.x)
x = torch.Size([34, 34])tensor([[1., 0., 0., ..., 0., 0., 0.], [0., 1., 0., ..., 0., 0., 0.], [0., 0., 1., ..., 0., 0., 0.], ..., [0., 0., 0., ..., 1., 0., 0.], [0., 0., 0., ..., 0., 1., 0.], [0., 0., 0., ..., 0., 0., 1.]])ここで、ノードの特徴行列xは単位行列です:ノードに関する重要な情報は含まれていません。年齢、スキルレベルなどの情報が含まれている可能性もありますが、このデータセットではそうではありません。つまり、ノードの分類は、単に接続を見ることで行われる必要があります。
次に、エッジのインデックスを出力しましょう。
print(f'edge_index = {data.edge_index.shape}')print(data.edge_index)
edge_index = torch.Size([2, 156])tensor([[ 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 10, 10, 10, 11, 12, 12, 13, 13, 13, 13, 13, 14, 14, 15, 15, 16, 16, 17, 17, 18, 18, 19, 19, 19, 20, 20, 21, 21, 22, 22, 23, 23, 23, 23, 23, 24, 24, 24, 25, 25, 25, 26, 26, 27, 27, 27, 27, 28, 28, 28, 29, 29, 29, 29, 30, 30, 30, 30, 31, 31, 31, 31, 31, 31, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33, 33], [ 1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 17, 19, 21, 31, 0, 2, 3, 7, 13, 17, 19, 21, 30, 0, 1, 3, 7, 8, 9, 13, 27, 28, 32, 0, 1, 2, 7, 12, 13, 0, 6, 10, 0, 6, 10, 16, 0, 4, 5, 16, 0, 1, 2, 3, 0, 2, 30, 32, 33, 2, 33, 0, 4, 5, 0, 0, 3, 0, 1, 2, 3, 33, 32, 33, 32, 33, 5, 6, 0, 1, 32, 33, 0, 1, 33, 32, 33, 0, 1, 32, 33, 25, 27, 29, 32, 33, 25, 27, 31, 23, 24, 31, 29, 33, 2, 23, 24, 33, 2, 31, 33, 23, 26, 32, 33, 1, 8, 32, 33, 0, 24, 25, 28, 32, 33, 2, 8, 14, 15, 18, 20, 22, 23, 29, 30, 31, 33, 8, 9, 13, 14, 15, 18, 19, 20, 22, 23, 26, 27, 28, 29, 30, 31, 32]])グラフ理論とネットワーク分析では、ノード間の接続性はさまざまなデータ構造を使用して格納されます。 edge_index はそのようなデータ構造の一つであり、グラフの接続は2つのリスト(156の有向辺、つまり78の双方向辺に相当)で格納されます。これら2つのリストの理由は、1つ目のリストがソースノードを格納し、2つ目のリストが宛先ノードを識別するためです。
この方法は座標リスト(COO)形式として知られており、疎行列を効率的に格納する手段です。疎行列は、ほとんどの要素がゼロである行列を効率的に格納するデータ構造です。COO形式では、非ゼロの要素のみが格納され、メモリと計算リソースを節約します。
対照的に、グラフの接続性を表すより直感的でわかりやすい方法は、隣接行列 A を使用することです。これは、各要素 Aᵢⱼ がグラフ内のノード i からノード j へのエッジの存在または不在を指定する正方行列です。つまり、非ゼロの要素 Aᵢⱼ はノード i からノード j への接続を意味し、ゼロは直接の接続がないことを示します。
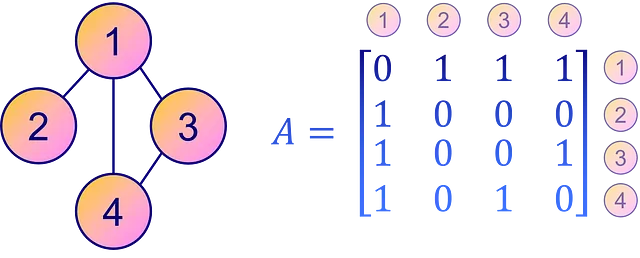
ただし、隣接行列は疎行列またはエッジが少ないグラフに対してはCOO形式よりもスペース効率が高くありません。ただし、明確さと簡単な解釈のために、隣接行列はグラフの接続性を表すための人気のある選択肢となっています。
隣接行列は、ユーティリティ関数 to_dense_adj() を使用して edge_index から推定することができます。
from torch_geometric.utils import to_dense_adj
A = to_dense_adj(data.edge_index)[0].numpy().astype(int)print(f'A = {A.shape}')print(A)
A = (34, 34)[[0 1 1 ... 1 0 0] [1 0 1 ... 0 0 0] [1 1 0 ... 0 1 0] ... [1 0 0 ... 0 1 1] [0 0 1 ... 1 0 1] [0 0 0 ... 1 1 0]]グラフデータでは、ノードが密接に接続されることは比較的まれです。ご覧のように、隣接行列 A は疎行列(ゼロで埋められたもの)です。
実世界の多くのグラフでは、ほとんどのノードが他のノードに対してわずかしか接続されていないため、隣接行列には多くのゼロが含まれます。これほど多くのゼロを格納することは非効率であり、これがPyGでCOO形式が採用される理由です。
一方、正解のラベルは理解しやすいです。
print(f'y = {data.y.shape}')print(data.y)
y = torch.Size([34])tensor([1, 1, 1, 1, 3, 3, 3, 1, 0, 1, 3, 1, 1, 1, 0, 0, 3, 1, 0, 1, 0, 1, 0, 0, 2, 2, 0, 0, 2, 0, 0, 2, 0, 0])y に格納されたノードの正解ラベルは、各ノードのグループ番号(0、1、2、3)を単純にエンコードしています。そのため、34の値が存在します。
最後に、トレーニングマスクを表示しましょう。
print(f'train_mask = {data.train_mask.shape}')print(data.train_mask)
train_mask = torch.Size([34])tensor([ True, False, False, False, True, False, False, False, True, False, False, False, False, False, False, False, False, False, False, False, False, False, False, False, True, False, False, False, False, False, False, False, False, False])トレーニングマスクは、True ステートメントでトレーニングに使用するノードを示しています。これらのノードはトレーニングセットを表し、他のノードはテストセットと見なすことができます。この分割は、モデル評価においてテスト用の未知のデータを提供するために役立ちます。
しかし、まだ終わっていません! Data オブジェクトにはさらに多くの機能があります。グラフのいくつかの特性を調査するためのさまざまなユーティリティ関数を提供します。例えば:
is_directed()はグラフが 有向 かどうかを示します。有向グラフは隣接行列が対称ではないことを意味し、つまりエッジの方向がノード間の接続に影響を与えます。isolated_nodes()はいくつかのノードが他のグラフに 接続されていない かどうかをチェックします。これらのノードは、接続がないため、分類などのタスクで課題を提起する可能性があります。has_self_loops()は少なくとも1つのノードが 自己に接続 しているかどうかを示します。これはループの概念とは異なります。ループは始点と終点が同じノードであり、間に他のノードを経由するパスを意味します。
Zacharyの空手クラブのデータセットのコンテキストでは、これらの特性はすべて False を返します。つまり、グラフは有向ではなく、孤立したノードは存在せず、ノードのいずれも自己に接続していません。
print(f'エッジは有向です:{data.is_directed()}')print(f'グラフに孤立したノードがあります:{data.has_isolated_nodes()}')print(f'グラフにループがあります:{data.has_self_loops()}')
エッジは有向です:Falseグラフに孤立したノードがあります:Falseグラフにループがあります:False最後に、PyTorch Geometric のグラフを人気のあるグラフライブラリ NetworkX に変換するには、to_networkx を使用します。これは、networkx と matplotlib を使用して小さなグラフを可視化するのに特に便利です。
各グループに異なる色を使用してデータセットをプロットしましょう。
from torch_geometric.utils import to_networkx
G = to_networkx(data, to_undirected=True)plt.figure(figsize=(12,12))plt.axis('off')nx.draw_networkx(G, pos=nx.spring_layout(G, seed=0), with_labels=True, node_size=800, node_color=data.y, cmap="hsv", vmin=-2, vmax=3, width=0.8, edge_color="grey", font_size=14 )plt.show()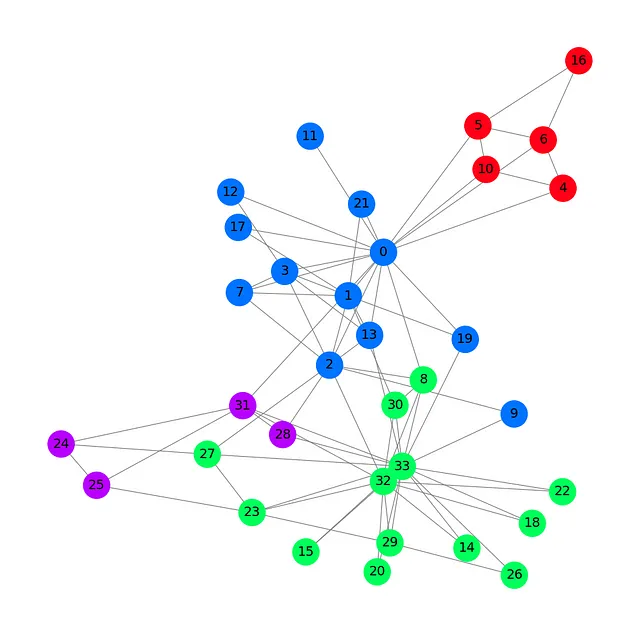
この Zacharyの空手クラブのプロットでは、34 のノード、78 (双方向) のエッジ、および 4 つの異なる色のラベルが表示されます。PyTorch Geometric を使用してデータセットを読み込み、処理する基本を見たので、グラフ畳み込みネットワークアーキテクチャを紹介します。
✉️ II. グラフ畳み込みネットワーク
このセクションでは、グラフ畳み込みレイヤーを基礎から構築して紹介します。
従来のニューラルネットワークでは、線形レイヤーは入力データに線形変換を適用します。この変換は入力特徴 x を重み行列 𝐖 を使用して隠れベクトル h に変換します。当面の間、バイアスは無視します。これは次のように表すことができます:
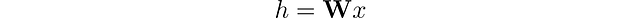
グラフデータでは、ノード間の接続を通じてさらなる複雑さが追加されます。これらの接続は重要です。通常、ネットワークでは、似たようなノード同士のリンクの方が異なるノードよりもリンクされやすいと仮定されています。この現象はネットワーク同一性として知られています。
ノードの表現を隣接するノードの特徴とマージすることで、ノード表現を豊かにすることができます。この操作は畳み込み、または近傍集約と呼ばれます。ノード i を含む自身を Ñ として表現しましょう。
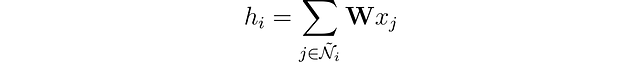
畳み込みニューラルネットワーク (CNN) のフィルターとは異なり、重み行列 𝐖 はユニークであり、すべてのノードで共有されます。しかし、別の問題があります。ノードはピクセルと異なり、固定された数の隣接ノードを持っていません。
1つのノードが1つの隣接ノードしか持たず、もう1つのノードが500個の隣接ノードを持つ場合、どのように対処すればよいでしょうか?もし単純に特徴ベクトルを合計した場合、500個の隣接ノードを持つノードの埋め込みhは非常に大きくなってしまいます。すべてのノードに対して値の「類似した範囲」を確保し、比較可能にするために、ノードの「次数」に基づいて結果を正規化することができます。ここで、次数とはノードが持つ接続の数を指します。
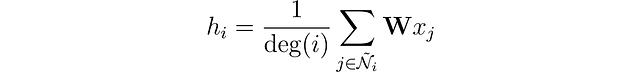
もう少しで完成です!Kipfらによって導入されたグラフ畳み込み層には、最後の改善点があります。
著者らは、多くの隣接ノードからの特徴が、より孤立したノードからの特徴よりも簡単に伝播することを観察しました。この効果を相殺するために、彼らは隣接ノードが少ないノードからの特徴に「大きな重み」を割り当てることを提案し、すべてのノードに影響をバランスさせました。この操作は次のように表されます:
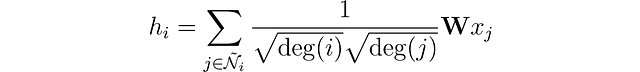
iとjが同じ数の隣接ノードを持つ場合、これは私たち自身の層と同等です。それでは、PythonとPyTorch Geometricでの実装方法を見てみましょう。
🧠 III. GCNの実装
PyTorch Geometricは、グラフ畳み込み層を直接実装するGCNConv関数を提供しています。
この例では、単一のGCN層、ReLU活性化関数、および線形出力層を持つ基本的なグラフ畳み込みネットワークを作成します。この出力層は、4つのカテゴリに対応する4つの値を生成し、最も高い値が各ノードのクラスを決定します。
次のコードブロックでは、3次元の隠れ層を持つGCN層を定義しています。
from torch.nn import Linearfrom torch_geometric.nn import GCNConv
class GCN(torch.nn.Module): def __init__(self): super().__init__() self.gcn = GCNConv(dataset.num_features, 3) self.out = Linear(3, dataset.num_classes) def forward(self, x, edge_index): h = self.gcn(x, edge_index).relu() z = self.out(h) return h, zmodel = GCN()print(model)
GCN( (gcn): GCNConv(34, 3) (out): Linear(in_features=3, out_features=4, bias=True))もし2つ目のGCN層を追加した場合、モデルは各ノードの隣接ノードだけでなく、これらの隣接ノードの隣接ノードからも特徴ベクトルを集約します。
より遠い値を集約するために、複数のグラフ層を積み重ねることができますが、注意が必要です。層を追加しすぎると、集約が非常に強力になり、すべての埋め込みが同じように見えるようになってしまいます。この現象は過剰平滑化と呼ばれ、層が多すぎる場合に本当の問題になることがあります。
GNNを定義したので、PyTorchで簡単なトレーニングループを書きましょう。マルチクラス分類タスクなので、通常のクロスエントロピー損失を選び、最適化手法としてAdamを使用します。この記事では、トレーニングとテストの分割は実装せず、GNNの学習方法に焦点を当てるためにシンプルに保ちます。
トレーニングループは標準的です:正しいラベルを予測し、GCNの結果をdata.yに格納された値と比較します。エラーはクロスエントロピー損失で計算され、Adamで逆伝播されてGNNの重みとバイアスを微調整します。最後に、10エポックごとにメトリクスを表示します。
criterion = torch.nn.CrossEntropyLoss()optimizer = torch.optim.Adam(model.parameters(), lr=0.02)
# 正確性を計算するdef accuracy(pred_y, y): return (pred_y == y).sum() / len(y)# アニメーション用のデータembeddings = []losses = []accuracies = []outputs = []# トレーニングループfor epoch in range(201): # 勾配をクリア optimizer.zero_grad() # 順伝播 h, z = model(data.x, data.edge_index) # 損失関数を計算 loss = criterion(z, data.y) # 正確性を計算 acc = accuracy(z.argmax(dim=1), data.y) # 勾配を計算 loss.backward() # パラメータを調整 optimizer.step() # アニメーション用のデータを保存 embeddings.append(h) losses.append(loss) accuracies.append(acc) outputs.append(z.argmax(dim=1)) # 10エポックごとにメトリクスを表示 if epoch % 10 == 0: print(f'Epoch {epoch:>3} | Loss: {loss:.2f} | Acc: {acc*100:.2f}%')
Epoch 0 | Loss: 1.40 | Acc: 41.18%Epoch 10 | Loss: 1.21 | Acc: 47.06%Epoch 20 | Loss: 1.02 | Acc: 67.65%Epoch 30 | Loss: 0.80 | Acc: 73.53%Epoch 40 | Loss: 0.59 | Acc: 73.53%Epoch 50 | Loss: 0.39 | Acc: 94.12%Epoch 60 | Loss: 0.23 | Acc: 97.06%Epoch 70 | Loss: 0.13 | Acc: 100.00%Epoch 80 | Loss: 0.07 | Acc: 100.00%Epoch 90 | Loss: 0.05 | Acc: 100.00%Epoch 100 | Loss: 0.03 | Acc: 100.00%Epoch 110 | Loss: 0.02 | Acc: 100.00%Epoch 120 | Loss: 0.02 | Acc: 100.00%Epoch 130 | Loss: 0.02 | Acc: 100.00%Epoch 140 | Loss: 0.01 | Acc: 100.00%Epoch 150 | Loss: 0.01 | Acc: 100.00%Epoch 160 | Loss: 0.01 | Acc: 100.00%Epoch 170 | Loss: 0.01 | Acc: 100.00%Epoch 180 | Loss: 0.01 | Acc: 100.00%Epoch 190 | Loss: 0.01 | Acc: 100.00%Epoch 200 | Loss: 0.01 | Acc: 100.00%素晴らしい!驚くほど、トレーニングセット(完全なデータセット)で100%の正確さに到達しました。これは、モデルが空手クラブのメンバーを正しいグループに正しく割り当てることを学んだことを意味します。
グラフをアニメーション化し、トレーニングプロセス中のGNNの予測の進化を見ることで、きれいな視覚化を作成できます。
%%capture
from IPython.display import HTML
from matplotlib import animation
plt.rcParams["animation.bitrate"] = 3000
def animate(i):
G = to_networkx(data, to_undirected=True)
nx.draw_networkx(G,
pos=nx.spring_layout(G, seed=0),
with_labels=True,
node_size=800,
node_color=outputs[i],
cmap="hsv",
vmin=-2,
vmax=3,
width=0.8,
edge_color="grey",
font_size=14
)
plt.title(f'エポック {i} | 損失: {losses[i]:.2f} | 正解率: {accuracies[i]*100:.2f}%',
fontsize=18, pad=20)
fig = plt.figure(figsize=(12, 12))
plt.axis('off')
anim = animation.FuncAnimation(fig, animate, \
np.arange(0, 200, 10), interval=500, repeat=True)
html = HTML(anim.to_html5_video())
display(html)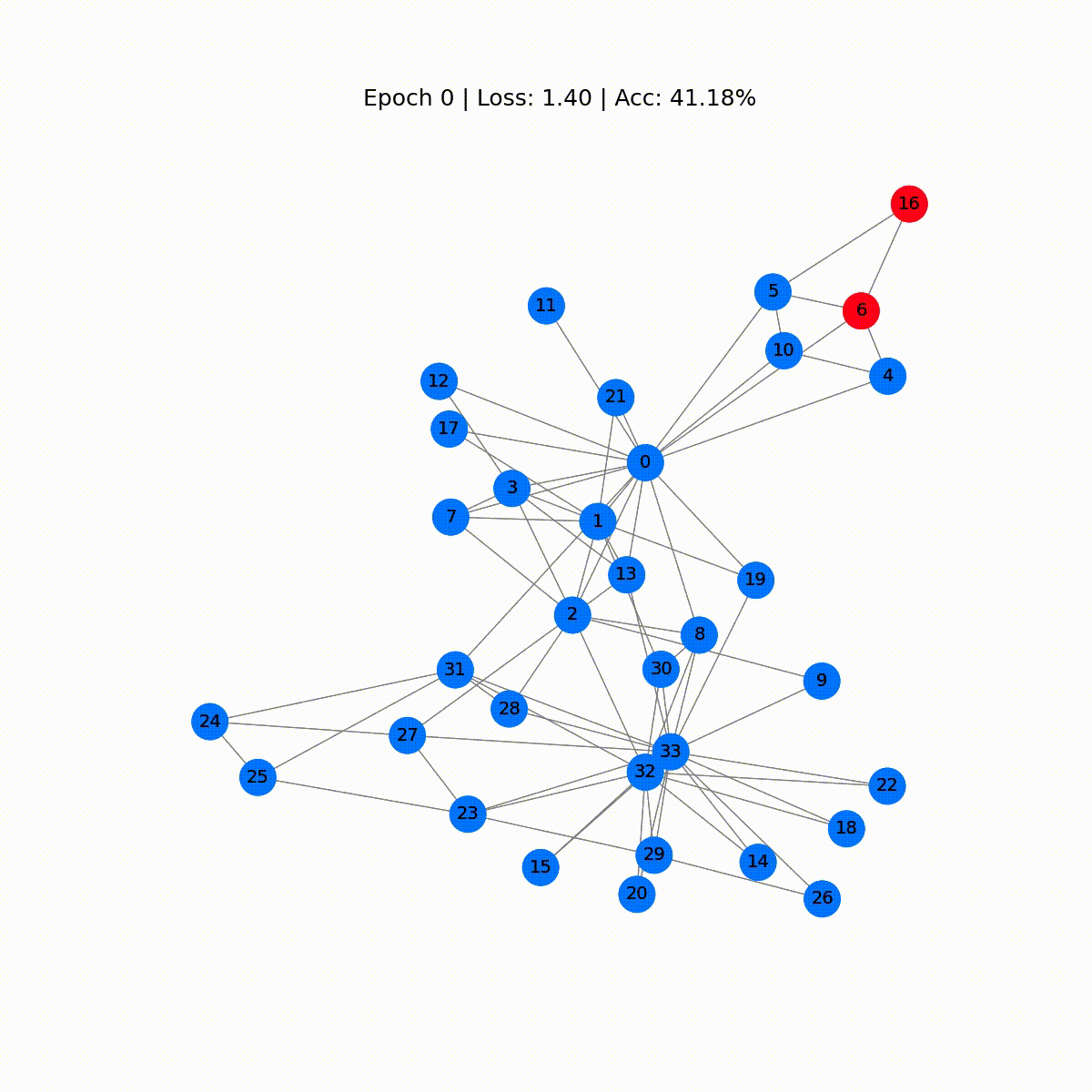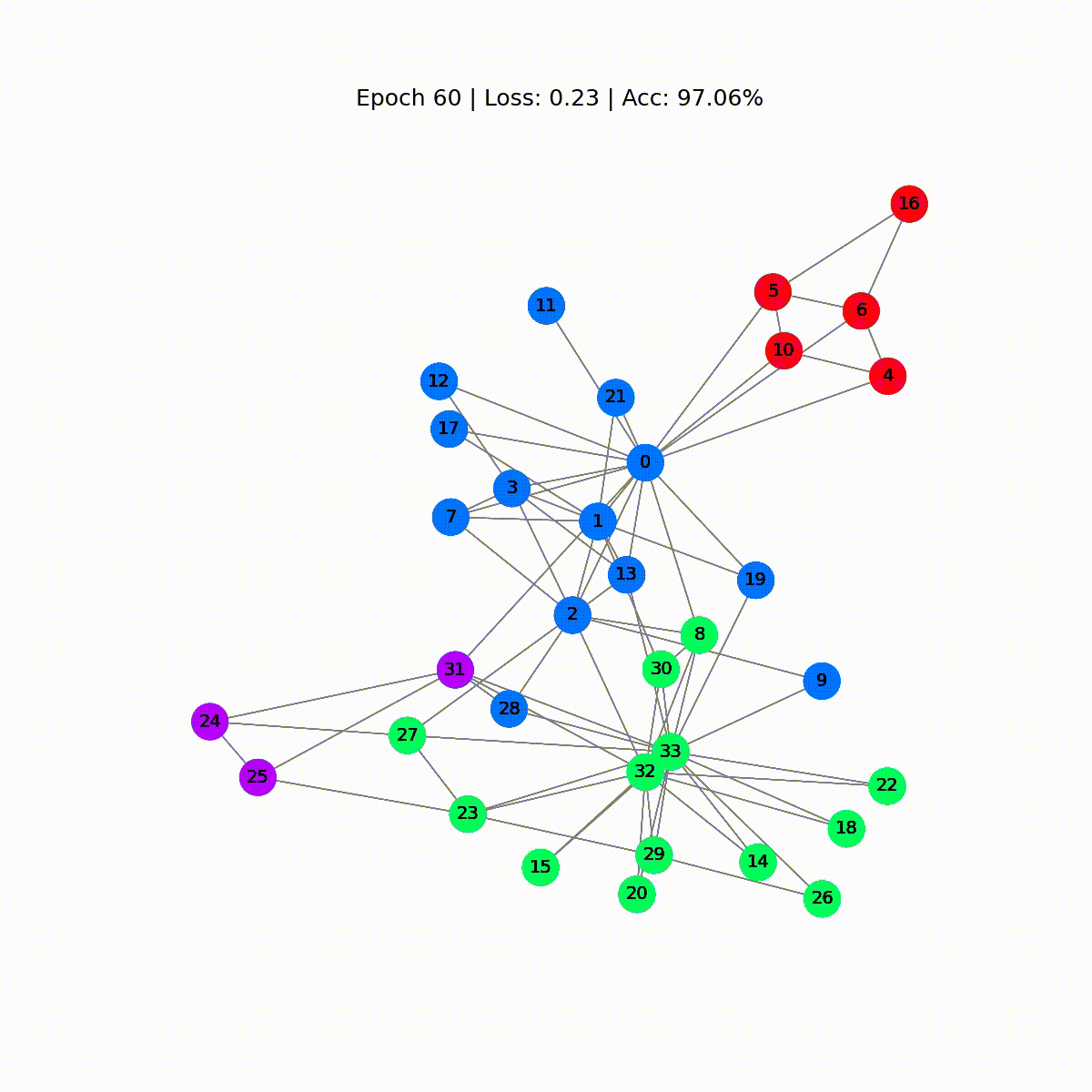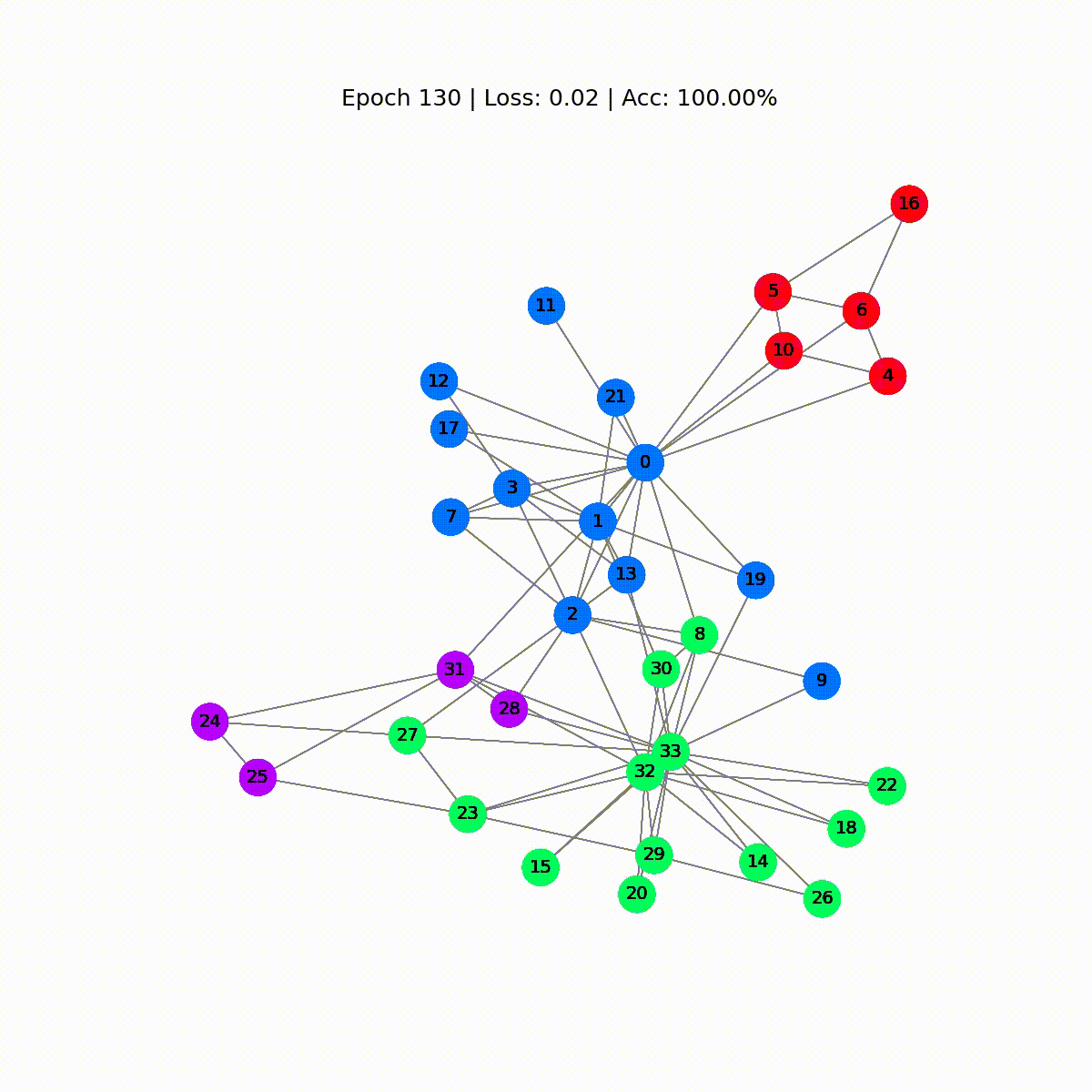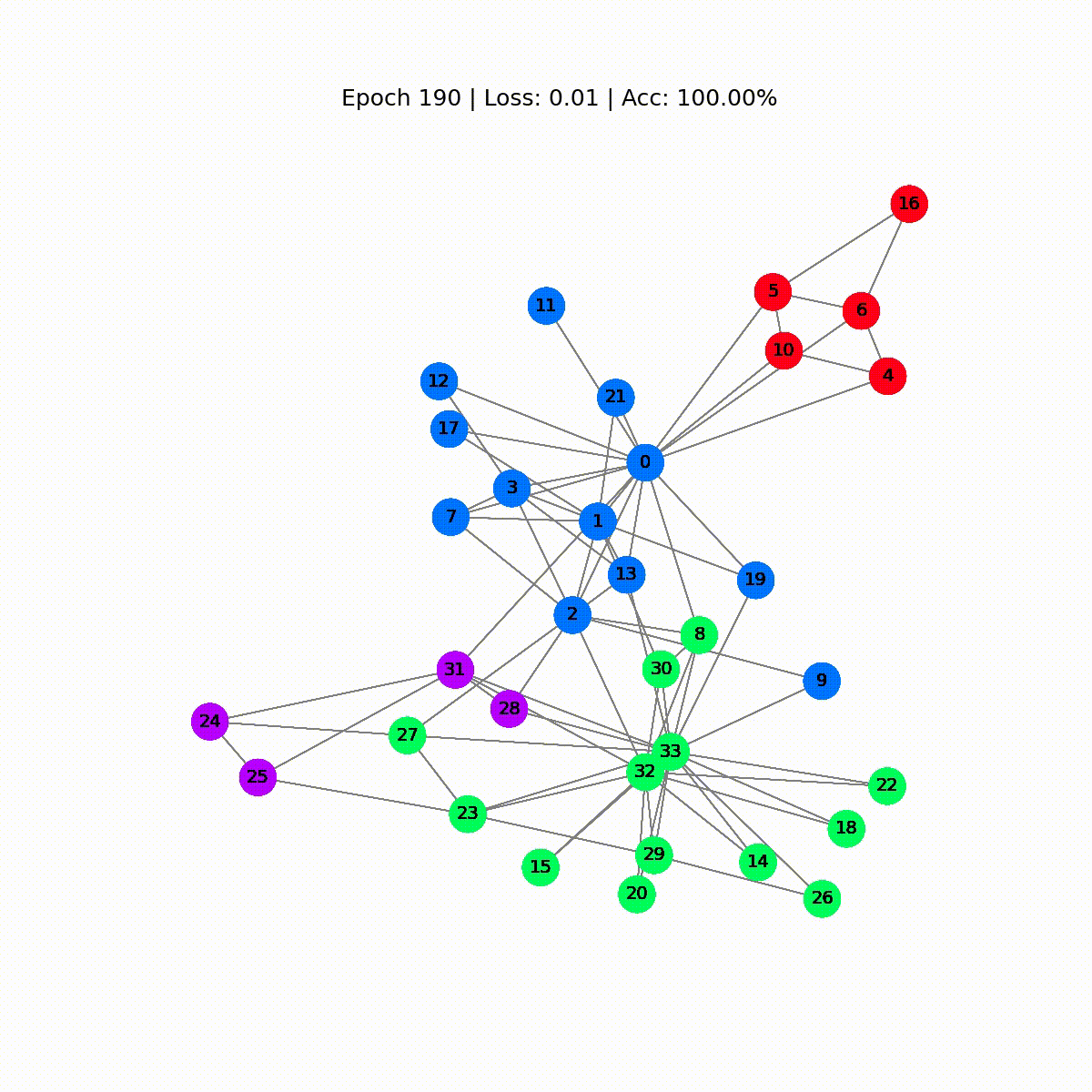
最初の予測はランダムですが、GCNはしばらくするとすべてのノードに正しくラベルを付けます。実際、最終的なグラフは、最初のセクションの終わりにプロットしたものと同じです。しかし、GCNは実際に何を学んでいるのでしょうか?
GNNは、隣接ノードからの特徴を集約することで、ネットワーク内のすべてのノードのベクトル表現(または埋め込み)を学習します。私たちのモデルでは、最終層はこれらの表現を使用して最適な分類を生成する方法を学習するだけです。ただし、埋め込みがGNNの真の成果物です。
モデルが学習した埋め込みを出力しましょう。
# 埋め込みを出力する
print(f'最終的な埋め込み = {h.shape}')
print(h)
最終的な埋め込み = torch.Size([34, 3])
tensor([[1.9099e+00, 2.3584e+00, 7.4027e-01],
[2.6203e+00, 2.7997e+00, 0.0000e+00],
[2.2567e+00, 2.2962e+00, 6.4663e-01],
[2.0802e+00, 2.8785e+00, 0.0000e+00],
[0.0000e+00, 0.0000e+00, 2.9694e+00],
[0.0000e+00, 0.0000e+00, 3.3817e+00],
[0.0000e+00, 1.5008e-04, 3.4246e+00],
[1.7593e+00, 2.4292e+00, 2.4551e-01],
[1.9757e+00, 6.1032e-01, 1.8986e+00],
[1.7770e+00, 1.9950e+00, 6.7018e-01],
[0.0000e+00, 1.1683e-04, 2.9738e+00],
[1.8988e+00, 2.0512e+00, 2.6225e-01],
[1.7081e+00, 2.3618e+00, 1.9609e-01],
[1.8303e+00, 2.1591e+00, 3.5906e-01],
[2.0755e+00, 2.7468e-01, 1.9804e+00],
[1.9676e+00, 3.7185e-01, 2.0011e+00],
[0.0000e+00, 0.0000e+00, 3.4787e+00],
[1.6945e+00, 2.0350e+00, 1.9789e-01],
[1.9808e+00, 3.2633e-01, 2.1349e+00],
[1.7846e+00, 1.9585e+00, 4.8021e-01],
[2.0420e+00, 2.7512e-01, 1.9810e+00],
[1.7665e+00, 2.1357e+00, 4.0325e-01],
[1.9870e+00, 3.3886e-01, 2.0421e+00],
[2.0614e+00, 5.1042e-01, 2.4872e+00],...
[2.1778e+00, 4.4730e-01, 2.0077e+00],
[3.8906e-02, 2.3443e+00, 1.9195e+00],
[3.0748e+00, 0.0000e+00, 3.0789e+00],
[3.4316e+00, 1.9716e-01, 2.5231e+00]], grad_fn=<ReluBackward0>)埋め込みは特徴ベクトルと同じ次元を持つ必要はありません。ここでは、次元数を34(dataset.num_features)から3に減らし、3Dの見栄えの良い可視化を得るために選びました。
トレーニングが行われる前のエポック0で、これらの埋め込みをプロットしましょう。
# Get first embedding at epoch = 0embed = h.detach().cpu().numpy()
fig = plt.figure(figsize=(12, 12))ax = fig.add_subplot(projection='3d')ax.patch.set_alpha(0)plt.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)ax.scatter(embed[:, 0], embed[:, 1], embed[:, 2], s=200, c=data.y, cmap="hsv", vmin=-2, vmax=3)plt.show()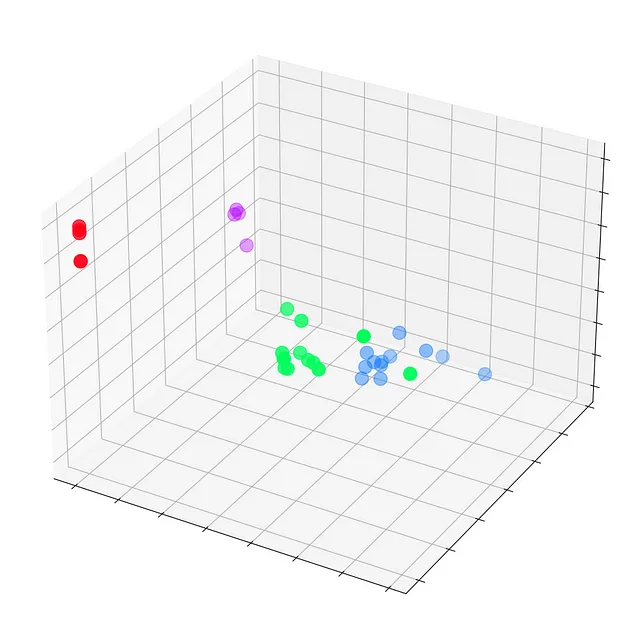
まだGNNがトレーニングされていないため、Zachary’s karate clubのすべてのノードは真のラベル(モデルの予測ではない)で散らばっています。しかし、トレーニングループの各ステップでこれらの埋め込みをプロットすると、GNNが実際に学習する内容を視覚化することができます。
ノードの分類に優れたGCNがどのように進化するか見てみましょう。
%%capture
def animate(i): embed = embeddings[i].detach().cpu().numpy() ax.clear() ax.scatter(embed[:, 0], embed[:, 1], embed[:, 2], s=200, c=data.y, cmap="hsv", vmin=-2, vmax=3) plt.title(f'Epoch {i} | Loss: {losses[i]:.2f} | Acc: {accuracies[i]*100:.2f}%', fontsize=18, pad=40)fig = plt.figure(figsize=(12, 12))plt.axis('off')ax = fig.add_subplot(projection='3d')plt.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)anim = animation.FuncAnimation(fig, animate, \ np.arange(0, 200, 10), interval=800, repeat=True)html = HTML(anim.to_html5_video())display(html)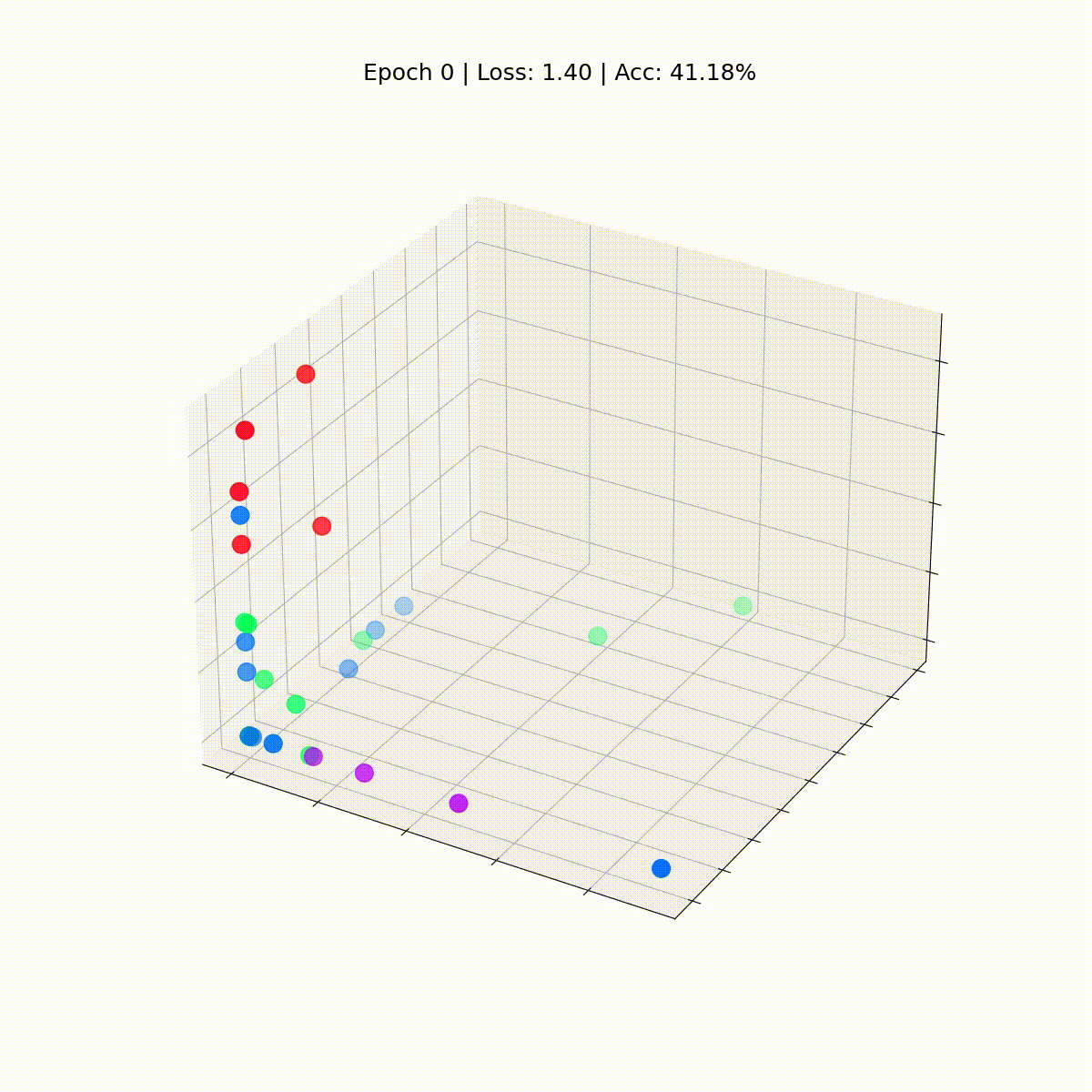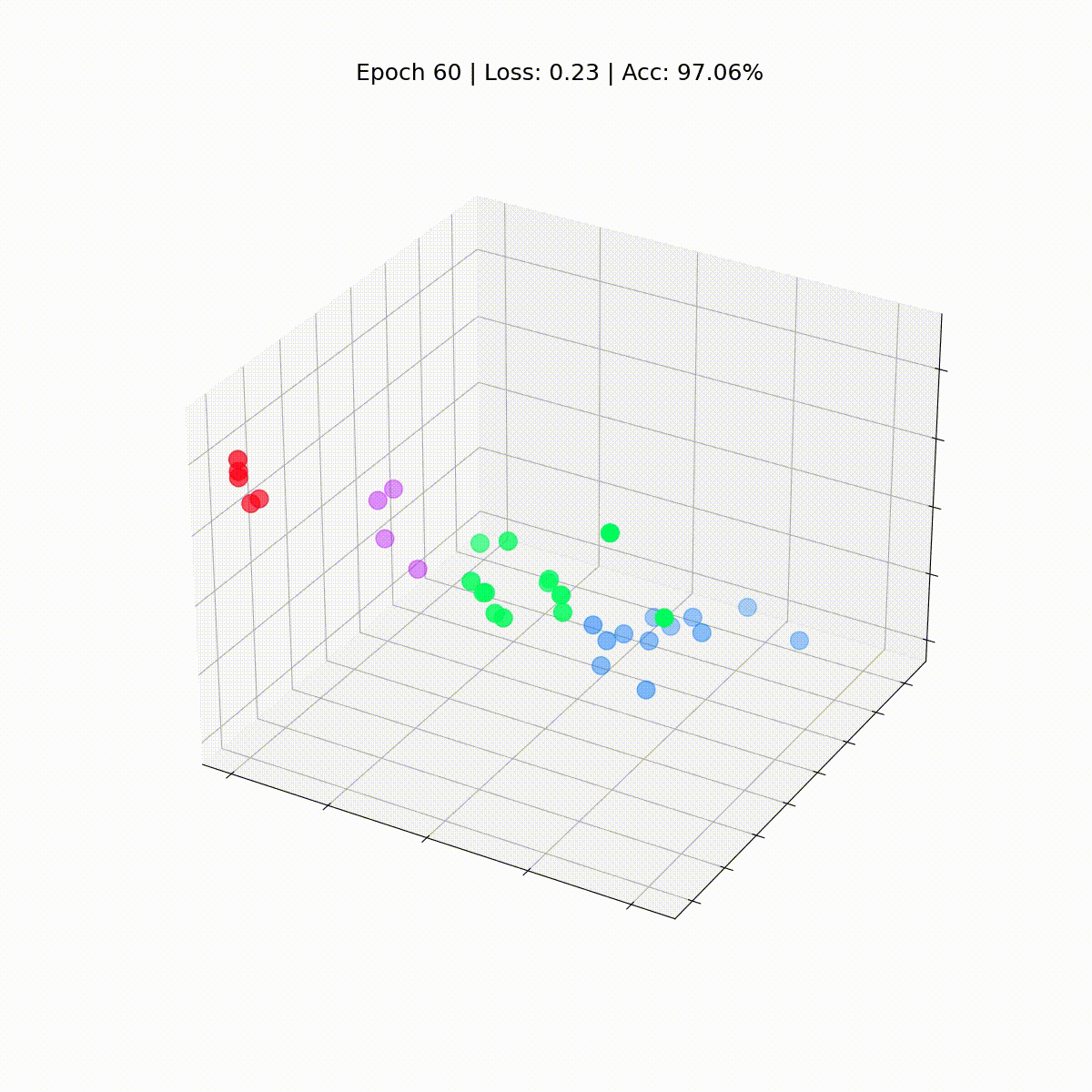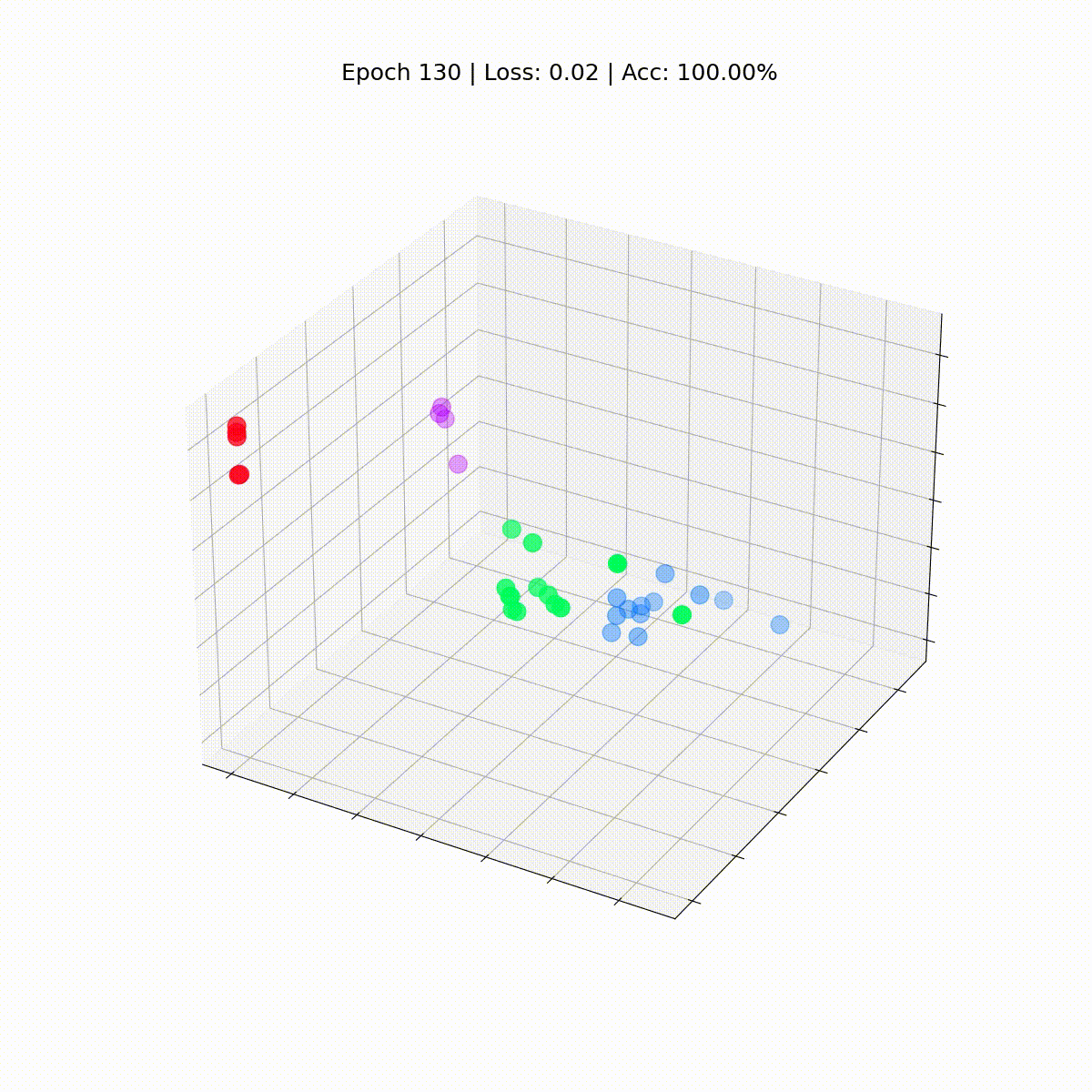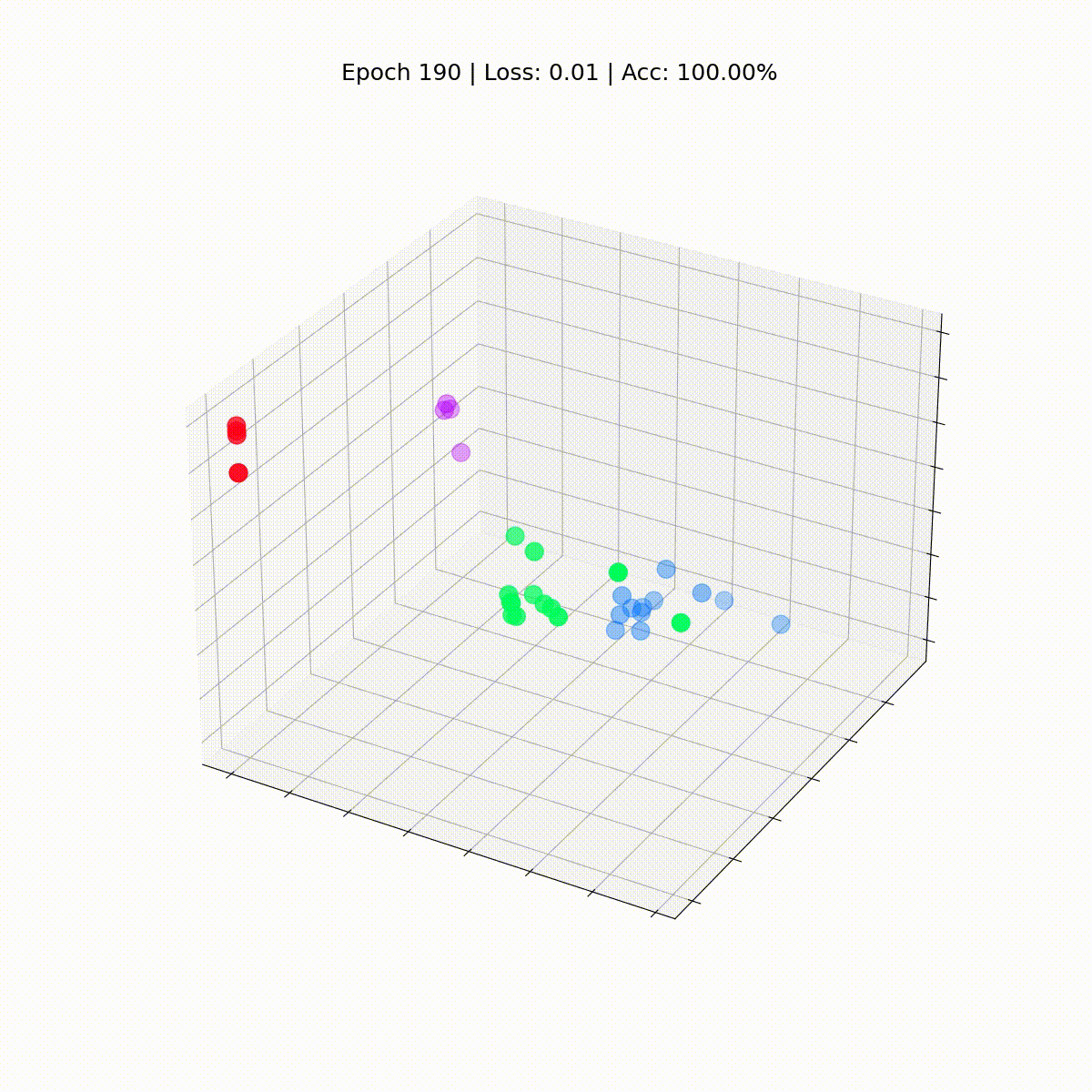
私たちのグラフ畳み込みネットワーク(GCN)は、似たようなノードを異なるクラスタにグループ化する埋め込みを効果的に学習しました。これにより、最終的な線形層がそれらを簡単に別々のクラスに区別することができます。
埋め込みはGNNに固有のものではありません。ディープラーニングの中でどこにでも存在します。また、必ずしも3Dである必要はありません。実際には、BERTのような言語モデルは768または1024次元の埋め込みを生成します。
追加の次元はノード、テキスト、画像などの情報をより詳細に保持しますが、それによって訓練がより困難な大きなモデルが作成されます。そのため、可能な限り低次元の埋め込みを保持することは有利です。
結論
グラフ畳み込みネットワークは、さまざまなコンテキストで適用できる非常に柔軟なアーキテクチャです。この記事では、PyTorch GeometricライブラリやDatasets、Dataなどのオブジェクトについて理解しました。次に、ゼロからグラフ畳み込み層を再構築することに成功しました。その後、GCNを実装することで、実践的な側面と各コンポーネントの相互作用について理解を深めました。最後に、トレーニングプロセスを視覚化し、そのネットワークにとって何を含むかを明確に把握しました。
Zachary’s karate clubは単純なデータセットですが、グラフデータとGNNの最も重要な概念を理解するには十分です。この記事ではノード分類についてのみ話しましたが、GNNは他のタスクも達成できます。たとえば、リンク予測(友達を推薦するため)、グラフ分類(分子をラベル付けするため)、グラフ生成(新しい分子を作成するため)などです。
GCN以外にも、多くのGNN層やアーキテクチャが研究者によって提案されています。次の記事では、Graph Attention Network(GAT)アーキテクチャを紹介します。これは、GCNの正規化因子と各接続の重要性を注意機構で動的に計算します。
グラフニューラルネットワークについてさらに詳しく知りたい場合は、私の書籍『Hands-On Graph Neural Networks』でGNNの世界に深く没頭してください。
次の記事
第2章:グラフ注意ネットワーク:セルフアテンションの説明
PyTorch Geometricを使用したセルフアテンションを持つGNNのガイド
towardsdatascience.com
機械学習についてさらに学び、1クリックで私の仕事をサポートしてください-こちらでVoAGIメンバーになる:
私の紹介リンクでVoAGIに参加-マキシム・ラボンヌ
VoAGIメンバーとして、会費の一部はあなたが読んだ作家に支払われ、すべてのストーリーに完全アクセスできます…
VoAGI.com
すでにメンバーの場合は、VoAGIで私をフォローできます。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles
