「ディープラーニングモデルのレイヤーを凍結する方法 – 正しいやり方」
Freezing Layers in Deep Learning Models - The Correct Way
PyTorchにおけるADAMオプティマイザの例
導入
モデルをファインチューニングしている際に、いくつかのパラメータをフリーズすることはよくあります。例えば、処理する例に応じていくつかの層をフリーズしたい場合などです。
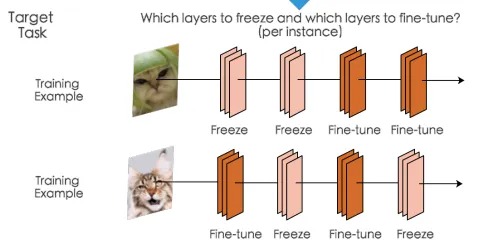
最初の例では、最初の2つの層をフリーズし、最後の2つのパラメータを更新しています。2番目の例では、2番目と4番目の層をフリーズし、他の層のファインチューニングを行います。このテクニックは役立つ場面がたくさんあり、この記事を読んでいる方にはおそらくそのようなケースがあるでしょう。
問題設定
少し簡単にするために、2つの異なるタイプの入力を受け入れるモデルがあると仮定しましょう。1つは3つの特徴量を持ち、もう1つは2つの特徴量を持ちます。そして、渡される入力に応じて、それぞれ異なる初期層を通過させることにします。したがって、トレーニング中には、それらの特定の入力に関連するパラメータのみを更新したいと思います。以下のように、input1 が渡された場合には hidden_task1 レイヤーをフリーズし、input2 が渡された場合には hidden_task2 レイヤーをフリーズしたいとします。
class Network(nn.Module): def __init__(self): super().__init__() # hidden layerへの入力としての線形変換 self.hidden_task1 = nn.Linear(3, 3, bias=False) self.hidden_task2 = nn.Linear(2, 3, bias=False) self.output = nn.Linear(3, 4, bias=False) # シグモイド活性化関数とソフトマックス出力を定義 self.sigmoid = nn.Sigmoid() self.softmax = nn.Softmax(dim=1) def forward(self, x, task='task1'): if task == 'task1': x = self.hidden_task1(x) else: x = self.hidden_task2(x) x = self.sigmoid(x) x = self.output(x) x = self.softmax(x) return x def freeze_params(self, params_str): for n, p in self.named_parameters(): if n in params_str: p.grad = None def freeze_params_grad(self, params_str): for n, p in self.named_parameters(): if n in params_str: p.requires_grad = False def unfreeze_params_grad(self, params_str): for n, p in self.named_parameters(): if n in params_str: p.requires_grad = True# inputとtargetを定義するinput1 = torch.randn(10, 3).to(device)input2 = torch.randn(10, 2).to(device)target1 = torch.randint(0, 4, (10, )).long().to(device) target2 = torch.randint(0, 4, (10, )).long().to(device) net = Network().to(device)# ヘルパー関数def changed_parameters(initial, final): for n, p in initial.items(): if not torch.allclose(p, final[n]): print("変更: ", n)SGDオプティマイザのみの世界で
SGDオプティマイザのみを使用している場合、requires_grad = False を使用することで、指定したパラメータの勾配を計算しないため、望む結果を得ることができます。
original_param = {n : p.clone() for (n, p) in net.named_parameters()}print("元のパラメータ ")pprint(original_param)print(100 * "=")# 2つの損失関数を定義しましょう(実際には1つだけ定義することもできますが、この場合は同じです)criterion1 = nn.CrossEntropyLoss()criterion2 = nn.CrossEntropyLoss()optimizer = optim.SGD(net.parameters(), lr=0.9)# 選択した層のrequires_gradをFalseに設定するnet.freeze_params_grad(['hidden_task2.weight'])print("タスク1の更新後のパラメータ ")params_hid1 = {n : p.clone() for (n, p) in net.named_parameters()}pprint(params_hid1)print(100 * "=")# タスク1の出力 - タスク2の層のパラメータをフリーズしたいoutput = net(input1, task='task1')optimizer.zero_grad() # 勾配バッファをゼロにするloss1 = criterion(output, target)loss1.backward()optimizer.step()print("オプティマイザの状態1: ")print(optimizer.state)# 選択した層のrequires_gradをTrueに戻すnet.unfreeze_params_grad(['hidden_task2.weight'])# タスク2の出力 - タスク1の層のパラメータをフリーズしたいoutput1 = net(input2, task='task2')optimizer.zero_grad() # 勾配バッファをゼロにするloss2 = criterion1(output1, target1)loss2.backward()optimizer.step() # 更新を行うprint("オプティマイザの状態1: ")print(optimizer.state)# 選択した層のrequires_gradをTrueに戻すnet.unfreeze_params_grad(['hidden_task1.weight'])print("タスク2の更新後のパラメータ ")params_hid2 = {n : p.clone() for (n, p) in net.named_parameters()}pprint(params_hid2)changed_parameters(params_hid1, params_hid2)以下の出力では、タスク1とタスク2の更新後の「Changed」パラメータが正しいことが分かり、望ましい結果が得られました。
{'hidden_task1.weight': tensor([[-0.0043, 0.3097, -0.4752], [-0.4249, -0.2224, 0.1548], [-0.0114, 0.4578, -0.0512]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[ 0.1871, -0.2137], [-0.1390, -0.6755], [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.0214, 0.2282, 0.3464], [-0.3914, -0.2514, 0.2097], [ 0.4794, -0.1188, 0.4320], [-0.0931, 0.0611, 0.5228]], device='cuda:0', grad_fn=<CloneBackward0>)}====================================================================================================hiddenの後のパラメータ {'hidden_task1.weight': tensor([[ 0.0010, 0.3107, -0.4746], [-0.4289, -0.2261, 0.1547], [-0.0105, 0.4596, -0.0528]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[ 0.1871, -0.2137], [-0.1390, -0.6755], [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.0554, 0.2788, 0.3800], [-0.4105, -0.2702, 0.1917], [ 0.4552, -0.1496, 0.4091], [-0.0838, 0.0601, 0.5301]], device='cuda:0', grad_fn=<CloneBackward0>)}====================================================================================================変更されました: hidden_task1.weight変更されました: output.weighthiddenの後のパラメータ 1 {'hidden_task1.weight': tensor([[ 0.0010, 0.3107, -0.4746], [-0.4289, -0.2261, 0.1547], [-0.0105, 0.4596, -0.0528]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[ 0.1906, -0.2102], [-0.1412, -0.6783], [-0.4657, -0.2929]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.0386, 0.2673, 0.3726], [-0.3818, -0.2414, 0.2232], [ 0.4402, -0.1698, 0.3898], [-0.0807, 0.0631, 0.5254]], device='cuda:0', grad_fn=<CloneBackward0>)}変更されました: hidden_task2.weight変更されました: output.weight適応型オプティマイザの複雑さ
今度は同じことを行ってみましょうが、Adamオプティマイザを使用します:
optimizer = optim.Adam(net.parameters(), lr=0.9)「Changed」の部分で、2番目のタスクの更新後にhidden_task1.weightも変更されてしまいましたが、これは望ましくありません。
元のパラメータ {'hidden_task1.weight': tensor([[-0.0043, 0.3097, -0.4752], [-0.4249, -0.2224, 0.1548], [-0.0114, 0.4578, -0.0512]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[ 0.1871, -0.2137], [-0.1390, -0.6755], [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.0214, 0.2282, 0.3464], [-0.3914, -0.2514, 0.2097], [ 0.4794, -0.1188, 0.4320], [-0.0931, 0.0611, 0.5228]], device='cuda:0', grad_fn=<CloneBackward0>)}====================================================================================================hiddenの後のパラメータ {'hidden_task1.weight': tensor([[ 0.8957, 1.2069, 0.4291], [-1.3211, -1.1204, -0.7465], [ 0.8887, 1.3537, -0.9508]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[ 0.1871, -0.2137], [-0.1390, -0.6755], [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.9212, 1.1262, 1.2433], [-1.2879, -1.1492, -0.6922], [-0.4249, -1.0177, -0.4718], [ 0.8078, -0.8394, 1.4181]], device='cuda:0', grad_fn=<CloneBackward0>)}====================================================================================================変更されました: hidden_task1.weight変更されました: output.weighthiddenの後のパラメータ 1 {'hidden_task1.weight': tensor([[ 1.4907, 1.7991, 1.0283], [-1.9122, -1.7133, -1.3428], [ 1.4837, 1.9445, -1.5453]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[-0.7146, -1.1118], [-1.0377, 0.2305], [-1.3641, -1.1889]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.9372, 1.3922, 1.5032], [-1.5886, -1.4844, -0.9789], [-0.8855, -1.5812, -1.0326], [ 1.6785, -0.2048, 2.3004]], device='cuda:0', grad_fn=<CloneBackward0>)}変更されました: hidden_task1.weight変更されました: hidden_task2.weight変更されました: output.weightここで何が起こっているかを理解してみましょう。SGDの更新ルールは次のように定義されています:
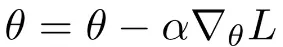
ここで、αは学習率、nabla Lはパラメータに関する勾配です。わかるように、勾配がゼロの場合、パラメータは更新されません。なぜなら、更新ルールは勾配の関数だけであり、勾配がゼロである場合、更新は行われないからです。そして、requires_grad = Falseと設定すると、それらのレイヤーの勾配はゼロになり、計算されません。
ADAMなどの適応的最適化手法では、更新ルールが勾配の関数だけでない場合はどうなるでしょうか?ADAMを見てみましょう:
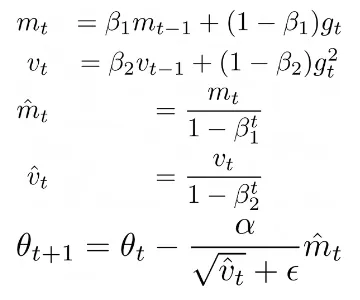
ここで、Beta1、Beta2はいくつかのハイパーパラメータであり、αは学習率、mtは勾配gtの第1モーメント、vtは勾配gtの第2モーメントです。この更新ルールにより、各パラメータに対して適応的な学習率を計算することができます。特に、現在の勾配gtがrequires_grad = Falseによってゼロに設定されていても、パラメータはオプティマイザによって保存されたmtおよびvtの値を使用して更新されます。実際に、optimizer.stateをプリントすると、オプティマイザが各パラメータの勾配の更新回数(つまり、勾配の更新回数)を保存していること、第1モーメントであるexp_avg、第2モーメントであるexp_avg_sqがわかります:
# optimizer step 1defaultdict(<class 'dict'>, {Parameter containing:tensor([[ 0.8957, 1.2069, 0.4291], [-1.3211, -1.1204, -0.7465], [ 0.8887, 1.3537, -0.9508]], device='cuda:0', requires_grad=True): {'step': tensor(1.), 'exp_avg': tensor([[-5.9304e-04, -1.0966e-04, -5.9985e-05], [ 4.4068e-04, 4.1636e-04, 1.7705e-05], [-1.0544e-04, -2.0357e-04, 1.7783e-04]], device='cuda:0'), 'exp_avg_sq': tensor([[3.5170e-08, 1.2025e-09, 3.5982e-10], [1.9420e-08, 1.7336e-08, 3.1345e-11], [1.1118e-09, 4.1440e-09, 3.1623e-09]], device='cuda:0')}, Parameter containing:tensor([[ 0.9212, 1.1262, 1.2433], [-1.2879, -1.1492, -0.6922], [-0.4249, -1.0177, -0.4718], [ 0.8078, -0.8394, 1.4181]], device='cuda:0', requires_grad=True): {'step': tensor(1.), 'exp_avg': tensor([[-0.0038, -0.0056, -0.0037], [ 0.0021, 0.0021, 0.0020], [ 0.0027, 0.0034, 0.0025], [-0.0010, 0.0001, -0.0008]], device='cuda:0'), 'exp_avg_sq': tensor([[1.4261e-06, 3.1517e-06, 1.3953e-06], [4.4782e-07, 4.3352e-07, 3.9994e-07], [7.2213e-07, 1.1702e-06, 6.4754e-07], [1.0547e-07, 1.2353e-09, 6.5470e-08]], device='cuda:0')}})# optimizer step 2tensor([[ 1.4907, 1.7991, 1.0283], [-1.9122, -1.7133, -1.3428], [ 1.4837, 1.9445, -1.5453]], device='cuda:0', requires_grad=True): {'step': tensor(2.), 'exp_avg': tensor([[-5.3374e-04, -9.8693e-05, -5.3987e-05], [ 3.9661e-04, 3.7472e-04, 1.5934e-05], [-9.4899e-05, -1.8321e-04, 1.6005e-04]], device='cuda:0'), 'exp_avg_sq': tensor([[3.5135e-08, 1.2013e-09, 3.5946e-10], [1.9400e-08, 1.7318e-08, 3.1314e-11], [1.1107e-09, 4.1398e-09, 3.1592e-09]], device='cuda:0')}, Parameter containing:tensor([[ 0.9372, 1.3922, 1.5032], [-1.5886, -1.4844, -0.9789], [-0.8855, -1.5812, -1.0326], [ 1.6785, -0.2048, 2.3004]], device='cuda:0', requires_grad=True): {'step': tensor(2.), 'exp_avg': tensor([[-0.0002, -0.0025, -0.0017], [ 0.0011, 0.0011, 0.0010], [ 0.0019, 0.0029, 0.0021], [-0.0028, -0.0015, -0.0014]], device='cuda:0'), 'exp_avg_sq': tensor([[2.4608e-06, 3.7819e-06, 1.6833e-06], [5.1839e-07, 4.8712e-07, 4.7173e-07], [7.4856e-07, 1.1713e-06, 6.4888e-07], [4.4950e-07, 2.6660e-07, 1.1588e-07]], device='cuda:0')}, Parameter containing:tensor([[-0.7146, -1.1118], [-1.0377, 0.2305], [-1.3641, -1.1889]], device='cuda:0', requires_grad=True): {'step': tensor(1.), 'exp_avg': tensor([[ 0.0009, 0.0011], [ 0.0045, -0.0002], [ 0.0003, 0.0012]], device='cuda:0'), 'exp_avg_sq': tensor([[8.7413e-08, 1.3188e-07], [1.9946e-06, 4.3840e-09], [8.1403e-09, 1.3691e-07]], device='cuda:0')}})最初のoptimizer.step()の更新では、オプティマイザの状態にはhidden_task1とoutputの2つのパラメータしかありません。2回目のオプティマイザのステップでは、すべてのパラメータがありますが、hidden_task1が2回更新されてしまっています。
では、どう対処するか?実際には非常にシンプルです。単にrequires_gradを使用する代わりに、パラメータにgrad = Noneを設定します。そのため、コードは次のようになります:
original_param = {n : p.clone() for (n, p) in net.named_parameters()}print("元のパラメータ")pprint(original_param)print(100 * "=")# 2つの損失関数を定義しましょう(実際には1つだけ定義してもかまいませんが、この場合は同じです)criterion1 = nn.CrossEntropyLoss()criterion2 = nn.CrossEntropyLoss()optimizer = optim.SGD(net.parameters(), lr=0.9)print("タスク1の更新後のパラメータ")params_hid1 = {n : p.clone() for (n, p) in net.named_parameters()}pprint(params_hid1)print(100 * "=")# タスク1の出力 - タスク2のレイヤーパラメータを凍結したいoutput = net(input1, task='task1')optimizer.zero_grad() # 勾配バッファをゼロにするloss1 = criterion1(output, target1)loss1.backward()# ここでパラメータを凍結!net.freeze_params(['hidden_task2.weight'])optimizer.step()# タスク2の出力 - タスク1のレイヤーパラメータを凍結したいoutput = net(input2, task='task2')optimizer.zero_grad() # 勾配バッファをゼロにするloss2 = criterion2(output, target2)loss2.backward()# ここでパラメータを凍結!net.freeze_params_grad(['hidden_task1.weight'])optimizer.step() # 更新を行うprint("タスク2の更新後のパラメータ")params_hid2 = {n : p.clone() for (n, p) in net.named_parameters()}pprint(params_hid2)changed_parameters(params_hid1, params_hid2)
loss.backward()の後にgrad = Noneを設定する必要があることに注意してください。なぜなら、最初にすべてのパラメータの勾配を計算する必要があるからですが、optimizer.step()の前に設定する必要があるからです。
コードを実行すると、ADAMオプティマイザの結果は予想通りです
元のパラメータ {'hidden_task1.weight': tensor([[-0.0043, 0.3097, -0.4752], [-0.4249, -0.2224, 0.1548], [-0.0114, 0.4578, -0.0512]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[ 0.1871, -0.2137], [-0.1390, -0.6755], [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.0214, 0.2282, 0.3464], [-0.3914, -0.2514, 0.2097], [ 0.4794, -0.1188, 0.4320], [-0.0931, 0.0611, 0.5228]], device='cuda:0', grad_fn=<CloneBackward0>)}====================================================================================================タスク1の更新後のパラメータ {'hidden_task1.weight': tensor([[ 0.8957, 1.2069, 0.4291], [-1.3211, -1.1204, -0.7465], [ 0.8887, 1.3537, -0.9508]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[ 0.1871, -0.2137], [-0.1390, -0.6755], [-0.4683, -0.2915]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.9212, 1.1262, 1.2433], [-1.2879, -1.1492, -0.6922], [-0.4249, -1.0177, -0.4718], [ 0.8078, -0.8394, 1.4181]], device='cuda:0', grad_fn=<CloneBackward0>)}====================================================================================================変更 : hidden_task1.weight変更 : output.weightタスク2の更新後のパラメータ {'hidden_task1.weight': tensor([[ 0.8957, 1.2069, 0.4291], [-1.3211, -1.1204, -0.7465], [ 0.8887, 1.3537, -0.9508]], device='cuda:0', grad_fn=<CloneBackward0>), 'hidden_task2.weight': tensor([[-0.7146, -1.1118], [-1.0377, 0.2305], [-1.3641, -1.1889]], device='cuda:0', grad_fn=<CloneBackward0>), 'output.weight': tensor([[ 0.9372, 1.3922, 1.5032], [-1.5886, -1.4844, -0.9789], [-0.8855, -1.5812, -1.0326], [ 1.6785, -0.2048, 2.3004]], device='cuda:0', grad_fn=<CloneBackward0>)}変更 : hidden_task2.weight変更 : output.weightまた、optimizer.stateは現在異なっています – 2番目のオプティマイザのステップではhidden_task1は更新されず、そのstepの値は1です。
tensor([[ 0.8957, 1.2069, 0.4291], [-1.3211, -1.1204, -0.7465], [ 0.8887, 1.3537, -0.9508]], device='cuda:0', requires_grad=True): {'step': tensor(1.), 'exp_avg': tensor([[-5.9304e-04, -1.0966e-04, -5.9985e-05], [ 4.4068e-04, 4.1636e-04, 1.7705e-05], [-1.0544e-04, -2.0357e-04, 1.7783e-04]], device='cuda:0'), 'exp_avg_sq': tensor([[3.5170e-08, 1.2025e-09, 3.5982e-10], [1.9420e-08, 1.7336e-08, 3.1345e-11], [1.1118e-09, 4.1440e-09, 3.1623e-09]], device='cuda:0')}, Parameter containing:tensor([[ 0.9372, 1.3922, 1.5032], [-1.5886, -1.4844, -0.9789], [-0.8855, -1.5812, -1.0326], [ 1.6785, -0.2048, 2.3004]], device='cuda:0', requires_grad=True): {'step': tensor(2.), 'exp_avg': tensor([[-0.0002, -0.0025, -0.0017], [ 0.0011, 0.0011, 0.0010], [ 0.0019, 0.0029, 0.0021], [-0.0028, -0.0015, -0.0014]], device='cuda:0'), 'exp_avg_sq': tensor([[2.4608e-06, 3.7819e-06, 1.6833e-06], [5.1839e-07, 4.8712e-07, 4.7173e-07], [7.4856e-07, 1.1713e-06, 6.4888e-07], [4.4950e-07, 2.6660e-07, 1.1588e-07]], device='cuda:0')}, Parameter containing:tensor([[-0.7146, -1.1118], [-1.0377, 0.2305], [-1.3641, -1.1889]], device='cuda:0', requires_grad=True): {'step': tensor(1.), 'exp_avg': tensor([[ 0.0009, 0.0011], [ 0.0045, -0.0002], [ 0.0003, 0.0012]], device='cuda:0'), 'exp_avg_sq': tensor([[8.7413e-08, 1.3188e-07], [1.9946e-06, 4.3840e-09], [8.1403e-09, 1.3691e-07]], device='cuda:0')}})分散データ並列
さらに追加の注意事項として、PyTorchで複数のGPUを使用してDistributedDataParallelをサポートする場合、上記で説明した実装を以下のように少し変更する必要があります:
少し複雑になりますが、もし書き方をもっと簡潔にする方法をご存知であれば、コメントで共有していただけると幸いです!
フィードバック
上記に関するフィードバックはいつでも歓迎します – この方法で問題が発生する可能性や同じ結果を得るための他の方法があるかどうかをご存知であれば教えていただけると幸いです。
結論
本記事では、トレーニング中に一部のレイヤーをフリーズおよびアンフリーズする必要がある場合のレイヤーのフリーズ方法について説明しました。トレーニング全体で一部のレイヤーを完全にフリーズしたい場合は、この記事で説明した両方の解決策を使用できます。ただし、トレーニング中にレイヤーをフリーズおよびアンフリーズする必要がある場合、勾配のみに依存するアップデートルールを持つ最適化手法とモメンタムなど他の変数に依存するアップデートルールを持つ最適化手法の振る舞いの違いが問題になることがわかりました。こちらでフルコードもご覧いただけます。
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles