非アーベル任意子の世界で初めてのブレードング

First Blade Runner in the world of non-Abelian anyons.

Google Quantum AIチームの研究員であるTrond AndersenとYuri Lenskyが投稿

同じ2つのオブジェクトを見せられて、目を閉じます。目を開けると、同じ2つのオブジェクトが同じ位置にあります。それらが交換されたかどうかをどのように判断できますか？直感と量子力学の法則は同意します：オブジェクトが本当に同じ場合、判断する方法はありません。

これは常識のように聞こえますが、これは私たちが知る3次元の世界にのみ適用されます。研究者たちは、2次元（2D）平面内でのみ移動することが制限された特別な粒子である任意子と呼ばれる特別なタイプの粒子に対して、量子力学がかなり異なるものを可能にすると予測しています。任意子は互いに区別できず、一部の非アーベル任意子は、交換時に共有量子状態の観測可能な差異を引き起こす特別な性質を持っており、互いに完全に区別できないにもかかわらず、交換されたときに判断できます。研究者たちは、その親戚であるアーベル任意子を検出することに成功しましたが、交換に対する変化が微妙で直接検出することができないため、「非アーベル交換行動」を実現することは、制御と検出の両方の課題によりより困難でした。

「超伝導プロセッサーにおけるグラフ頂点の非アーベル結び目」では、この非アーベル交換行動を初めて観測しました。非アーベル任意子は、粒子を交換し、まるでストリングが絡まるように交換し合うことで量子演算が実現される新しい方法を開く可能性があります。私たちの超伝導量子プロセッサーでこの新しい交換行動を実現することは、環境ノイズに対して頑強であるという利点を持つトポロジカル量子計算の代替ルートになる可能性があります。

• A.I.が建築家に職場デザインの変革をもたらす方法
• サンタクララ大学を卒業した早熟なティーンプロディジー
• メンテナンス・プロセスの標準化におけるコンピュータ化されたメンテナンス・マネジメント・システムの役割

交換統計と非アーベル任意子

この奇妙な非アーベル的な振る舞いがどのように発生するかを理解するには、2本のストリングを結ぶことの類比が役立ちます。同じ2本のストリングを取り、互いに平行に置きます。その後、エンドを交換してダブルヘリックス形状を形成します。ストリングは同じですが、エンドを交換するときにお互いを巻き込むため、エンドが交換されたときは非常に明確になります。

非アーベル任意子の交換は、同様の方法で視覚化できます。ここでは、ストリングは、粒子の位置を時間次元に拡張して「ワールドライン」を形成することによって作成されます。2つの粒子の位置を時間に対してプロットすることを想像してください。粒子がその場にとどまる場合、プロットは単に、それらの定常位置を表す2本の平行線になります。しかし、粒子の場所を交換すると、ワールドラインがお互いに絡み合います。2回交換すると、結び目ができます。

少し視覚化するのは難しいですが、4次元（3つの空間プラス1つの時間次元）の結び目は常に簡単に解除できます。それらは自明です。シューレースのように、片方の端を引っ張って解きます。しかし、粒子が2次元空間に制限されている場合、結び目は3次元にあり、私たちの日常的な3Dの生活から知っているように、常に簡単には解除できません。非アーベル任意子のワールドラインの結び目は、粒子の状態を変換するための量子計算操作として使用できます。

非アーベル任意子の重要な側面は「退化度」です。いくつかの分離された任意子の完全な状態はローカル情報によって完全に指定されるわけではなく、同じ任意子構成はいくつかの量子状態の重ね合わせを表すことができます。非アーベル任意子を互いに巻き付けることで、エンコードされた状態が変化する可能性があります。

非アーベル任意子の作り方

Googleの量子プロセッサーの1つで非アーベル結び目を実現するにはどうすればよいでしょうか？私たちは最近、量子誤り訂正のマイルストーンを達成したサーフェスコードから始めます。量子ビットはチェッカーボードパターンの頂点に配置されます。チェッカーボードの各色の正方形は、正方形の四隅にある量子ビットの2つの可能な共同測定の1つを表します。これらの「スタビライザー測定」は、+または-1の値を返すことができます。後者はプラケット違反と呼ばれ、単一量子ビットのXおよびZゲートを適用して、斜めに作成および移動できます（チェスのビショップのように）。最近、これらのビショップのようなプラケット違反はアーベル任意子であることを示しました。非アーベル任意子とは対照的に、アーベル任意子の状態は、交換されたときにわずかに変化します。非常に微妙で、直接検出することは不可能です。アーベル任意子は興味深いですが、非アーベル任意子ほどトポロジカル量子計算にとって有望ではありません。

非アーベルアニオンを生成するには、 degeneracy（つまり、すべてのスタビライザー測定が+1になる波動関数の数）を制御する必要があります。スタビライザー測定は2つの可能な値を返すため、各スタビライザーはシステムの degeneracy を半分に減らし、十分な数のスタビライザーで、1つの波動関数だけが基準を満たすようになります。したがって、 degeneracy を増やす簡単な方法は、2つのスタビライザーを合併することです。そうすることで、スタビライザーグリッドから1つのエッジを除去し、3つのエッジが交差する2つの点が生じます。これらの点は、「degree-3 vertices」（D3Vs）と呼ばれ、非アーベルアニオンであると予測されています。

D3Vをブレードするためには、それらを動かす必要があります。つまり、スタビライザーを新しい形に伸ばしたり、圧縮したりする必要があります。これは、アニオンとその近隣の間に2キュビットゲートを実装することによって実現します（下の中央と右のパネルを参照）。

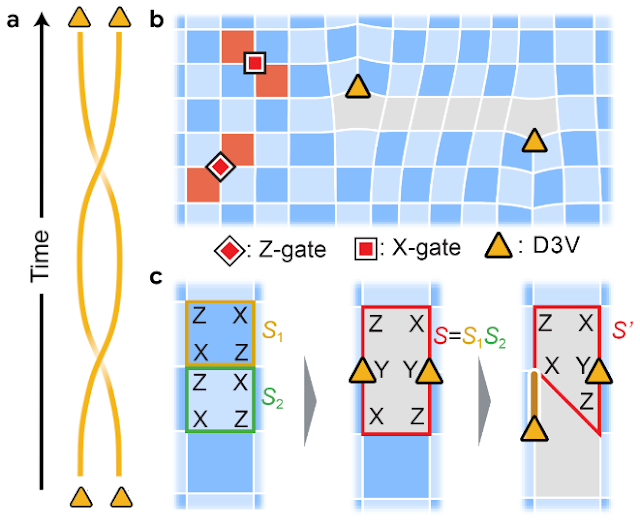スタビライザーコード内の非アーベルアニオン。a: 2つのアニオンのワールドラインをブレードして作られた結び目の例。b: 単一キュビットゲートを使用して値が-1のスタビライザー（赤い正方形）を作成および移動できます。チェスのビショップのように、これらは斜めにしか動くことができず、通常の表面コードでは1つのサブレイティスに制限されています。この制限は、D3V（黄色い三角形）が導入されると破られます。c: D3Vを形成および移動するためのプロセス（非アーベルアニオンと予測されています）。各正方形は、その角にある4つのキュビットの合同測定に対応します（左パネル）。2つの隣接する正方形を分離するエッジを除去することで、すべての6つのキュビットの単一の合同測定があるようにします（中央パネル）。これにより、2つのD3Vが作成され、これらは非アーベルアニオンです。私たちは、近隣サイト間の2キュビットゲートを適用することで、D3Vを移動させます（右パネル）。

これで、非アーベルアニオンを作成および移動する方法がわかりました。次に、彼らのアニオニックな振る舞いを検証する必要があります。これには、非アーベルアニオンが期待される3つの特性を調べます：

1. 「融合規則」-非アーベルアニオンが互いに衝突したときに何が起こるか？
2. 交換統計-互いに編み込まれたときに何が起こるか？
3. トポロジカル量子コンピューティングの基礎-非アーベルアニオンに量子ビットをエンコードし、ブレードを使用して2キュビットエンタングル操作を実行できるか？

非アーベルアニオンの融合規則

私たちは、D3Vのペアが上述のビショップのようなプラケット違反とどのように相互作用するかを調べることで、融合規則を調べます。特に、これらのペアを作成し、1つを単一キュビットゲートを適用してD3Vの周りに持っていきます。

チェスのビショップのルールでは、プラケット違反は決して会うことができませんが、チェッカーボード格子の変位により、ルールを破り、パートナーと出会い、それと消滅することができます。プラケット違反は消えました！しかし、非アーベルアニオンを再び互いに接触させると、アニオンは突然消えて、欠落しているプラケット違反に変形します。このような振る舞いがどんなに奇妙に思えても、これらのエンティティが従う融合規則の正確な表現です。これにより、D3Vが実際に非アーベルアニオンであることが確認されます。

任意の融合規則のデモンストレーション（下部左側のパネルIから開始）。2つのD3V（黄色い三角形）を作成し、2つの隣接するプラケット違反（赤い正方形）を形成して、そのうちの1つをD3Vの間に渡します。 D3Vの「チェス盤」の変形により、プラケット違反のビショップルールが変化します。以前は隣接する正方形にあったので、同じ対角線に沿って移動し、衝突することができます（赤い線に示されています）。衝突すると、互いに消滅します。 D3Vを再び近づけると、驚くべきことに、隣接する赤いプラケット違反に変形します。

非アーベル交換統計の観測

融合規則を確立した後、非アーベル・エニオンの本物の証拠である非アーベル交換統計を見たいと思います。二つの非アーベル・エニオンのペアを作成し、それぞれから一つずつ取り出して他方のものを巻きつけることで、それらを編ませます（下図参照）。二つのペアを再び融合すると、二つのプラケット違反のペアが現れます。エニオンを互いに編ませるという単純な行為によって、システムの観測量が変化したのです。つまり、非アーベル・エニオンが交換される間、目を閉じていても、目を開けた後に交換されたことがわかるようになっているのです。これが非アーベル統計の特徴です。

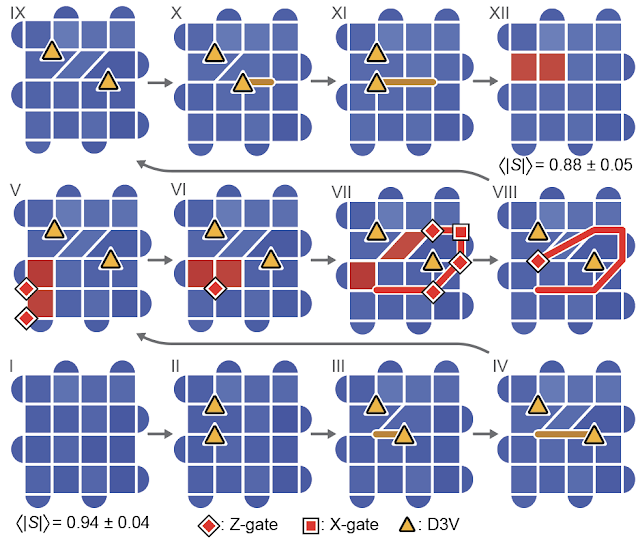
非アーベル・エニオンを編む。D3Vの二つのペアを作成し、それぞれから一つずつ取り出して他方のものを巻きつける（ III-XI ）。パネルXIIで二つのプラケット違反のペアが現れる！非アーベル・エニオンを編むことで、システムの観測量がパネルIからパネルXIIに変化し、非アーベル交換統計の明確な現れになっています。

トポロジカル量子計算

融合規則と交換統計を確立した後、これらの粒子を量子計算に使用する方法を示します。非アーベル・エニオンは、論理キュビットで表される情報をエンコードするために使用できます。これは、実験で使用される実際の物理キュビットと区別する必要があります。N D3Vsにエンコードされた論理キュビットの数は、N /2–1になるため、N =8 D3Vsを使用して三つの論理キュビットをエンコードし、編ませてからから絡み合わせます。その結果得られる状態を研究することで、編み込みによって望ましいグリーンバーガー・ホーン・ツァイリンガー（GHZ）状態が形成されたことが確認されます。

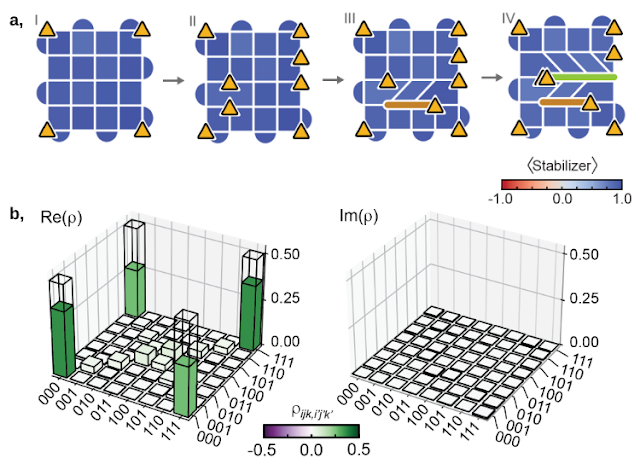非アーベル・エニオンを論理キュビットとして使用する。 a, 8つのD3Vsにエンコードされた三つのキュビットを絡み合わせるために非アーベル・エニオンを編み込む。 b, 量子状態トモグラフィーにより、密度行列を再構成し、3Dバープロットで表すことができ、望ましい高度に絡み合ったGHZ状態と一致することがわかる。

結論

私たちの実験は、非アーベル交換統計の最初の観測と、D3Vsを編ませることで量子計算を実行することができることを示しています。編み込み手順中のエラー訂正を含む将来の追加要素により、キュビットに固有の弾力性を付与し、計算中に誤りが発生しないようにするための長年にわたる探求であるトポロジカル量子計算に向けた重要な一歩となる可能性があります。

謝辞

このブログ記事の執筆に協力してくれた、私たちの量子科学コミュニケーターであるKatie McCormickに感謝します。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!