施設分散問題：混合整数計画モデル

Facility Dispersion Problem Mixed Integer Programming Model

p-分散と最大和モデルに関する包括的なPythonチュートリアル

一部の施設配置問題では、他の施設の影響を遮らないように配置する必要があります。リスク軽減、競争回避、その他の考慮事項によって駆動されている場合でも、これらの課題の解決をマスターすることは、オペレーションズリサーチツールキットでの重要なスキルです。

Kuby（1987）は、これらの問題のための2つの異なる混合整数計画（MIP）の定式化を提案しました：p-分散問題と最大和問題。この記事では、PythonライブラリPyomoとHiGHSソルバーを使用して、両方を実装します。

これらのモデルに加えて、いくつかの有用なモデリングリソースも紹介します。まず、バイナリ変数の積を線形計画問題の文脈で線形化するための戦略です。最大化の目的を考慮すると、この問題では明示的に必要ではありません。次に、選択された場合にセットのアイテムの任意のパラメータよりも小さい何かを最大化しようとする最大最小MIPの定式化です。最後に、2つのモデルの要素を組み合わせた、優先順位の明確に定義された階層で複数の目標を解決するための戦略です。

数値最適化にまだ慣れていない興味を持っている方は、この記事を読む前に私の以前の記事である「線形計画法」と「分岐限定法」について見ておくと役に立つかもしれません。

• 「ワードエンベディング：より良い回答のためにチャットボットに文脈を与える」
• BERTopicを使用したクラスごとのトピック
• 「NVIDIAがインドの巨大企業と提携し、世界最大の人口を持つ国でAIを進める」

通常どおり、完全なコードはこのgitリポジトリで見つけることができます。

これらの場所のうち、5つの施設を配置するためにどれを選びますか？

バイナリ変数の積

この問題の基本要素を定義する際、選択された場合に1の値を取り、それ以外の場合は0となるバイナリ変数を使用することができます。これらの変数をxᵢとします。2つの場所間の距離（または他の分散メトリック）が事前に計算されているとし、これらをdᵢⱼとしましょう。選択された任意の施設のペアの分散をどのように計算することができるでしょうか？

バイナリ変数xᵢとxⱼの積を使用して、それらがソリューションに含まれる場合に得られる非類似度を計算することは、ある程度直感的です。しかし、これは二次の定式化になり、そのため線形ソルバーを適用することはできません。幸いなことに、MIPでバイナリ変数の積を定式化する方法がいくつかの制約を使用してあります。

有向グラフG(V, A)と、ノードiとjが選択されていることを示す新しいバイナリ変数zᵢⱼを考えます。iまたはjのいずれかが選択されていない場合、zᵢⱼは0でなければなりません。これにより、最初の制約グループが得られます：

現時点では、iとjの両方が選択されていても、zᵢⱼは0の値を取る可能性があります。したがって、iとjが選択された場合にzᵢⱼが1になるような追加の制約を含める必要があります。

最大和問題のようにzᵢⱼに比例する何かを最大化する場合、2つ目の制約グループは不要です。なぜなら、zᵢⱼに比例する利益を計算しない方が意味がないからです。ただし、他のMIPモデルを定式化する際には、この制約が役立つことがあります。

以下のセクションでは、これらの概念を最大和問題に適用しましょう。

最大和モデル

離散最大和問題では、N個の離散ノードのうちp個の施設の位置を定義し、選択された施設のすべてのペア間で計算される距離（または距離の平均）の合計を最大化する必要があります。したがって、施設は有向グラフG（V、A）で配置されたノードです。iからjへの各アークの重みは、事前にわかっている距離（分散）メトリックdᵢⱼです。また、位置iが選択された場合を示すバイナリ変数xᵢと、iとjの両方が選択された場合を示すバイナリ変数zᵢⱼを考慮してください。

目的は次のように述べることができます：

前のセクションで示されたバイナリ変数の積を線形化する制約に加えて、p個の位置が選択されることを保証する制約を含める必要があります。

したがって、問題の制約条件は次のように述べることができます：

Pythonを使用してコードに変換しましょう。そのためには、使用するライブラリをインポートする必要があります。線形代数計算とランダムな座標点の作成にはnumpyライブラリを使用します。scipyのsquareformとpdist関数は、座標の行列が与えられた場合に距離を計算するために使用されます。matplotlibは可視化ツールであり、pyomoは代数モデリング言語（AML）（ソルバーHiGHSと共に）です。

import numpy as npfrom scipy.spatial.distance import squareform, pdistimport matplotlib.pyplot as pltimport pyomo.environ as pyofrom pyomo.contrib.appsi.solvers.highs import Highs

N個の点を作成し、そのうちいくつが施設の位置として選択される必要があるかを定義する必要があります。コードの実行ごとにランダムシード（12）を固定することで、紹介で示されている点を取得できます。

# ランダムシードを固定np.random.seed(12)# ランダムな点を作成N = 25p = 5coordinates = np.random.random((N, 2))# ペア間の距離を計算distances = squareform(pdist(coordinates))

これで、pyomoモデルを開始するために必要な要素が揃いました。

pyomoで問題をモデル化するには2つのアプローチがあります：Abstract ModelとConcrete Modelです。Abstract Modelの場合、問題の代数的な表現がいくつかのデータ値が供給される前に定義されます。一方、Concrete Modelの場合、モデルインスタンスはその要素が定義されるとすぐに作成されます。これらのアプローチについては、ライブラリのドキュメンテーションやBynum et al.（2021）の書籍で詳しく説明されています。この記事では、Concrete Modelの定式化を採用します。

model = pyo.ConcreteModel()

このモデルには、ノードとアークの2つのセットがあります。完全な有向グラフを考慮しているため、ノード間のすべてのペアにはアークが存在します（ノード自体へのアークは除く）。

# ノードとアークのセットmodel.V = pyo.Set(initialize=range(N))model.A = pyo.Set(initialize=[(i, j) for i in model.V for j in model.V if i != j])

事前に提供されたパラメータは、選択されるノードの数とノード間の距離です。

# パラメータmodel.d = pyo.Param(model.A, initialize={(i, j): distances[i, j] for (i, j) in model.A})model.p = pyo.Param(initialize=p)

次に、決定変数を含めましょう。

# 決定変数model.x = pyo.Var(model.V, within=pyo.Binary)model.z = pyo.Var(model.A, within=pyo.Binary)

そして、制約条件も含めましょう…

# p個のノードが選択されるdef p_selection(model):    return sum(model.x[:]) == model.p# 開始ノードが選択されていない場合、アークは0def dispersion_c1(model, i, j):    return model.z[i, j] <= model.x[i]# 終了ノードが選択されていない場合、アークは0def dispersion_c2(model, i, j):    return model.z[i, j] <= model.x[j]# 制約条件をモデルに含めるmodel.p_selection = pyo.Constraint(rule=p_selection)model.dispersion_c1 = pyo.Constraint(model.A, rule=dispersion_c1)model.dispersion_c2 = pyo.Constraint(model.A, rule=dispersion_c2)

最後に、目的関数を作成する必要があります。

def disp_obj(model):    return sum(model.z[i, j] * model.d[i, j] for (i, j) in model.A)model.obj = pyo.Objective(rule=disp_obj, sense=pyo.maximize)

これで最大値モデルが解決する準備が整いました。次に、Pyomoと互換性のあるソルバーをインスタンス化する必要があります。Highsソルバーは、highspyパッケージがインストールされている場合、バージョン6.4.3以降のPyomoで利用可能です。したがって、pip install highspyを実行してください。

solver = Highs()solver.solve(model)

そして、計算時間約120秒後に、以下の結果が得られます。

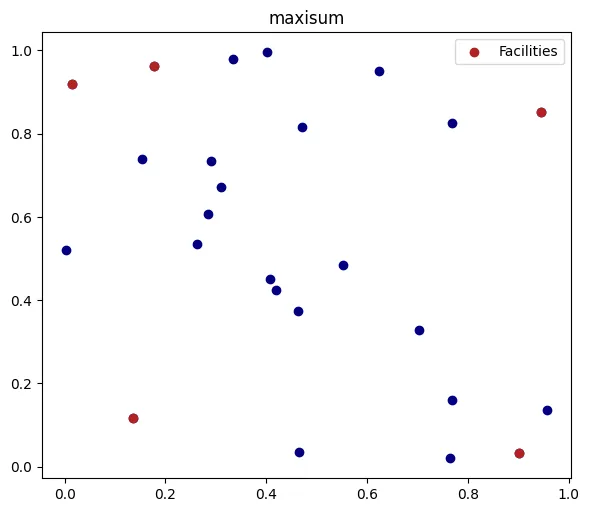
全体の分散が最大化されているにもかかわらず、左上の2つの施設はまだ非常に近くにあり、望ましくない可能性があります。したがって、最大値モデルの代わりに、選択されたノードの任意のペア間の最小距離を最大化するp-分散モデルがあります。

p-分散モデル

p-分散モデルでは、選択されたノード間の最小距離を計算するための追加の決定変数が必要です。これが最大化する目標です。この変数をDとします。iとjの両方が選択される場合、Dがdᵢⱼ以下であることを保証するbig M制約を作成する必要があります。そうでない場合は、Dが無制限であることを保証する必要があります。zᵢⱼを2進変数の積として定式化した場合、この追加の制約は次のようになります。

この定式化では、Mは任意の値のDに対して制約(i, j)の実行可能性を保証するために使用される任意に大きな固定パラメータですが、モデルの線形緩和が整数バージョンに似ているために収束が容易になるようにできるだけ小さくする必要があります。この問題では、dᵢⱼの最大値が興味深い代替手段となります。

この定式化はこのモデルには適していますが、変数zᵢⱼをモデルに含めないより簡潔なアプローチも使用できます。

この定式化では、xᵢまたはxⱼがゼロに等しいことは、不等式がDの任意の値に対して有効であることを保証する十分な条件です。そして、目的は単純にDを最大化することになります。

次に示すPythonコードでは、前のモデルと同じセットやパラメータ、および意思決定変数xを持つ新しいモデルを考えます。

# 最大最小制約def maxmin_rule(model, i, j):    return model.D <= model.d[i, j] + model.M * (1 - model.x[i]) + model.M * (1 - model.x[j])# 新しいパラメータ big Mmodel.M = max(model.d[:, :])# 新しい変数model.D = pyo.Var(within=pyo.NonNegativeReals)# 新しい制約model.maxmin_rule = pyo.Constraint(model.A, rule=maxmin_rule)# 目的関数model.obj = pyo.Objective(expr=model.D, sense=pyo.maximize)

そして、ソルバーを呼び出した後、以下の結果が1.2秒未満で得られました。

場所が空間的によく分散しているように思えます。

この分散を改善する方法はありますか？

多基準アプローチ

p-分散モデルの目的関数は、選択されたノードの間の最小距離にのみ依存することを覚えておいてください。したがって、この距離を定義する2つの点と、それらの間の距離が目的自体以上であるか等しい他の点の組み合わせを使用して、いくつかの解が得られることがあります。これらの代替案の中から最良のものを選択することによって、ソリューションを洗練することはできますか？これにつながるのは、Kuby（1987）が提案した2段階の「多基準アプローチ」です。

最初のステップでは、p-分散モデルが最適に解かれ、現在の目的がパラメータd_optに保存されます。それから、D ≥ d_optを保証する追加の制約を持つ最大和モデルが解かれ、p-分散モデルの最適解の中で、最大の総分散を持つものが得られます。

Pythonでこれを行うためには、p-分散モデルがインスタンス化され、最大和モデルの決定変数と制約も持っているとします。

# D must be optimaldef composed_constr(model):    return model.D >= model.d_opt# Solve p-dispersionsolver.solve(model)# New parametermodel.d_opt = pyo.Param(initialize=model.obj())# Deactivate old objectivemodel.obj.deactivate()# More variablesmodel.z = pyo.Var(model.A, within=pyo.Binary)# Solution will not make the current D worsemodel.composed_constr = pyo.Constraint(rule=composed_constr)# New objectivemodel.obj_disp = pyo.Objective(rule=disp_obj, sense=pyo.maximize)solver.solve(model)

そして、これは驚くほど速いです。ソルバーが2つ目の目的に入るとき、実行可能な代替案の空間は大幅に小さくなります。1秒未満で、以下の結果が得られます。

さらなる読み物

顧客が均等に分布していない、施設の容量が制限されている、または適切な施設の数が事前にわからない場合、おそらく異なる施設配置問題に直面しているかもしれません。Balinski（1965）の定式化をPythonで実装したものは、Nicolo Cosimo Albaneseによるこの素晴らしい記事でPuLPを使用しています。

最適化：Pythonにおける容量制約付き施設配置問題

コストを削減し需要を満たすための最適な倉庫の数と場所を見つける

towardsdatascience.com

結論

この記事では、施設分散問題のための2つの混合整数計画モデルをPythonでPyomoを使用して実装しました。先行研究で確認されたように、maxisumモデルは要素を空間に均等に分布させない場合がありますが、p-分散モデルは空間的によく広がり、均等に分布した解を生成します。最大和目的は、最適解の集合から最大の総分散を持つものを選択するために、p-分散モデルの解を洗練するために使用することができます。これらの例で使用される完全なコードは、さらなる利用のために利用可能です。

参考文献

Balinski, M. L. 1965. Integer programming: methods, uses, computations. Management science, 12(3), 253–313.

Bynum, M. L., Hackebeil, G. A., Hart, W. E., Laird, C. D., Nicholson, B. L., Siirola, J. D., … & Woodruff, D. L. 2021. Pyomo-optimization modeling in python (Vol. 67). Berlin/Heidelberg, Germany: Springer.

Kuby, M. J. 1987. Programming models for facility dispersion: The p‐dispersion and maxisum dispersion problems. Geographical Analysis, 19(4), 315–329.

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!