新しい方法で純粋な数学の美しさを探索する

'Exploring the beauty of pure mathematics in a new way.'

100年以上前、スリニヴァーサ・ラマヌジャンは、他の誰も見つけることのできない驚くべき数のパターンを見るという非凡な能力で数学界を驚かせました。このインド出身の独学の数学者は、彼の洞察を深く直感的で霊的であると表現し、パターンはしばしば鮮明な夢の中で彼に現れました。これらの観察は、純粋な数学の抽象的な世界の驚異的な美しさと絶対的な可能性を捉えています。近年では、AIが深い人間の直感に関わる分野での突破を達成し、最近では科学の中でも最も難しい問題に取り組んでいますが、最新のAI技術は純粋な数学の研究においては重要な成果を上げていませんでした。

DeepMindの知能解決の使命の一環として、私たちは機械学習（ML）を用いて数学的な構造とパターンを認識し、数学者がそれまでに見つけることのなかった発見への導きを支援する可能性を探求しました。これにより、AIが純粋数学の最前線で助けになることが初めて示され、MLがどのように使われるかを他の数学者に提案しました。

私たちの研究論文は、トポロジーと表現論の2つの純粋数学の分野での新しい洞察を見つけるためにトップの数学者との共同研究を詳細に紹介しています。シドニー大学のジョーディ・ウィリアムソン教授との共同研究では、数十年にわたって解決されなかった順列に関する予想についての新しい公式を発見しました。オックスフォード大学のマーク・ラッケンビー教授とアンドラーシュ・ユハーズ教授との共同研究では、結び目の構造を研究することで、数学の異なる分野の予想外の関連性を発見しました。これらは、数学のトップ研究者から見ても、機械学習によって行われた初めての重要な数学的発見です。私たちは、それぞれの結果についてarXivでの完全な補足論文を公開し、適切な数学のジャーナルに提出する予定です。これらの例を通じて、これらのツールが他の数学者によって新しい結果を達成するためにどのように使用されるかを提案します。

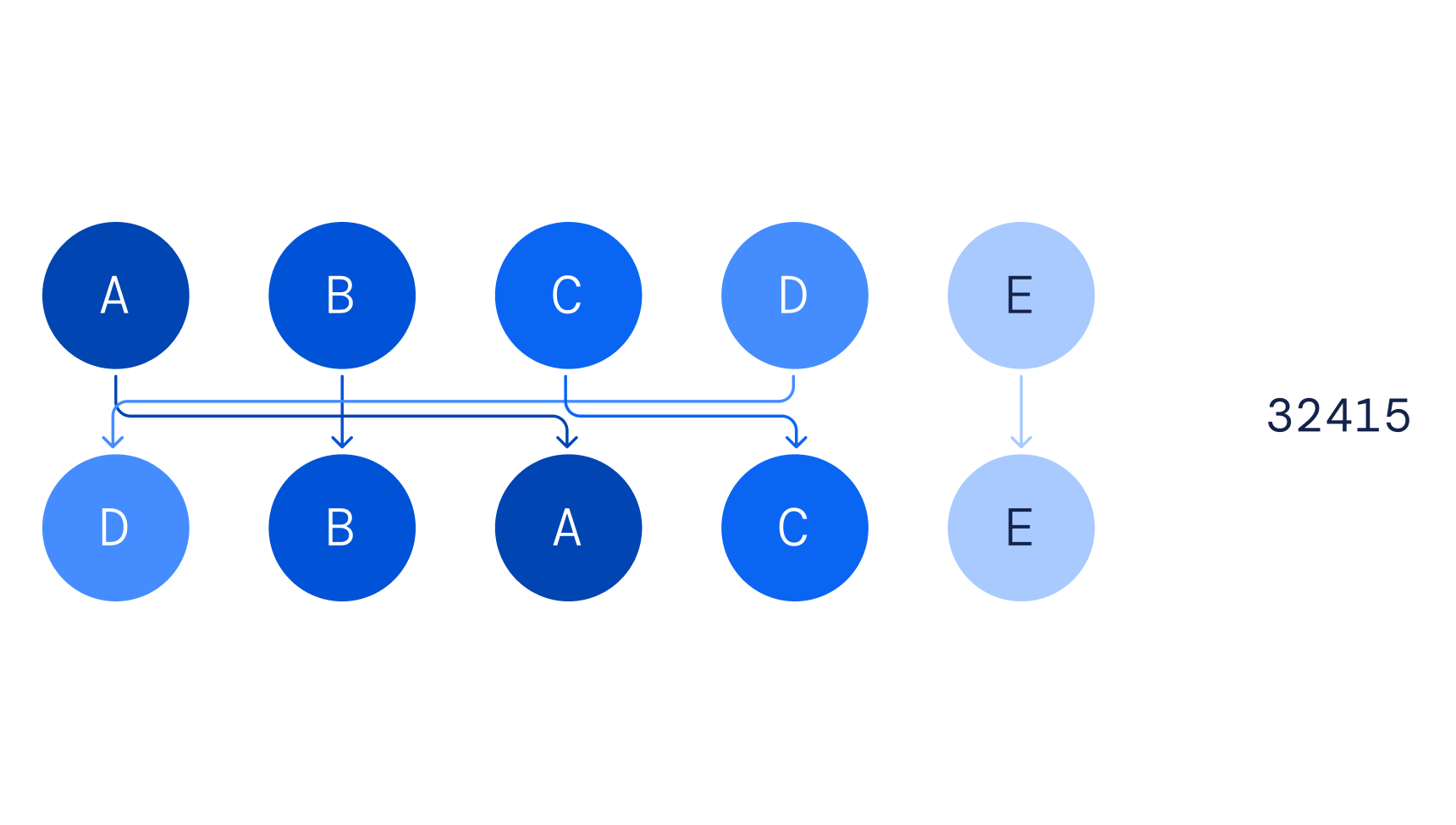
私たちが調査した2つの基本的な対象は、結び目と順列です。

• スケールにおける言語モデリング：Gopher、倫理的考慮事項、および情報の検索
• AIを用いて量子スケールで物質をシミュレーションする
• MuZeroの研究から現実世界への第一歩

多くの年にわたり、数学者はパターンの検索を支援するためにコンピュータを使用してデータを生成してきました。これは実験数学として知られ、バーチ・スウィンナートン・ダイア予想などのよく知られた予想を生み出しました。このような方法は成功しており、一般的に行われていますが、このデータからのパターンの識別と発見は主に数学者に頼っていました。

パターンの発見は、純粋数学においてさらに重要になってきました。現在、数学者が一生をかけて研究することができるデータよりも多くのデータを生成することが可能になりました。数千次元のような興味深い対象は、直接推論するのが非常に困難な場合もあります。これらの制約を考慮して、私たちはAIが数学者の新しい洞察を全く新しい方法でサポートできると信じています。

それは、ガリレオが望遠鏡を手に取り、データの宇宙を深く覗き込み、それまでに検出されなかったものを見ることができるようになる感覚です。 マーカス・デュ・ソート、オックスフォード大学の科学の公共理解のためのシモニー教授および数学の教授

私たちの結果は、MLが数学の研究を補完し、教師あり学習によって仮説されたパターンの存在を検出し、機械学習の属性技術によってこれらのパターンに対する洞察を提供することで、問題に対する直感を導くことができることを示唆しています。

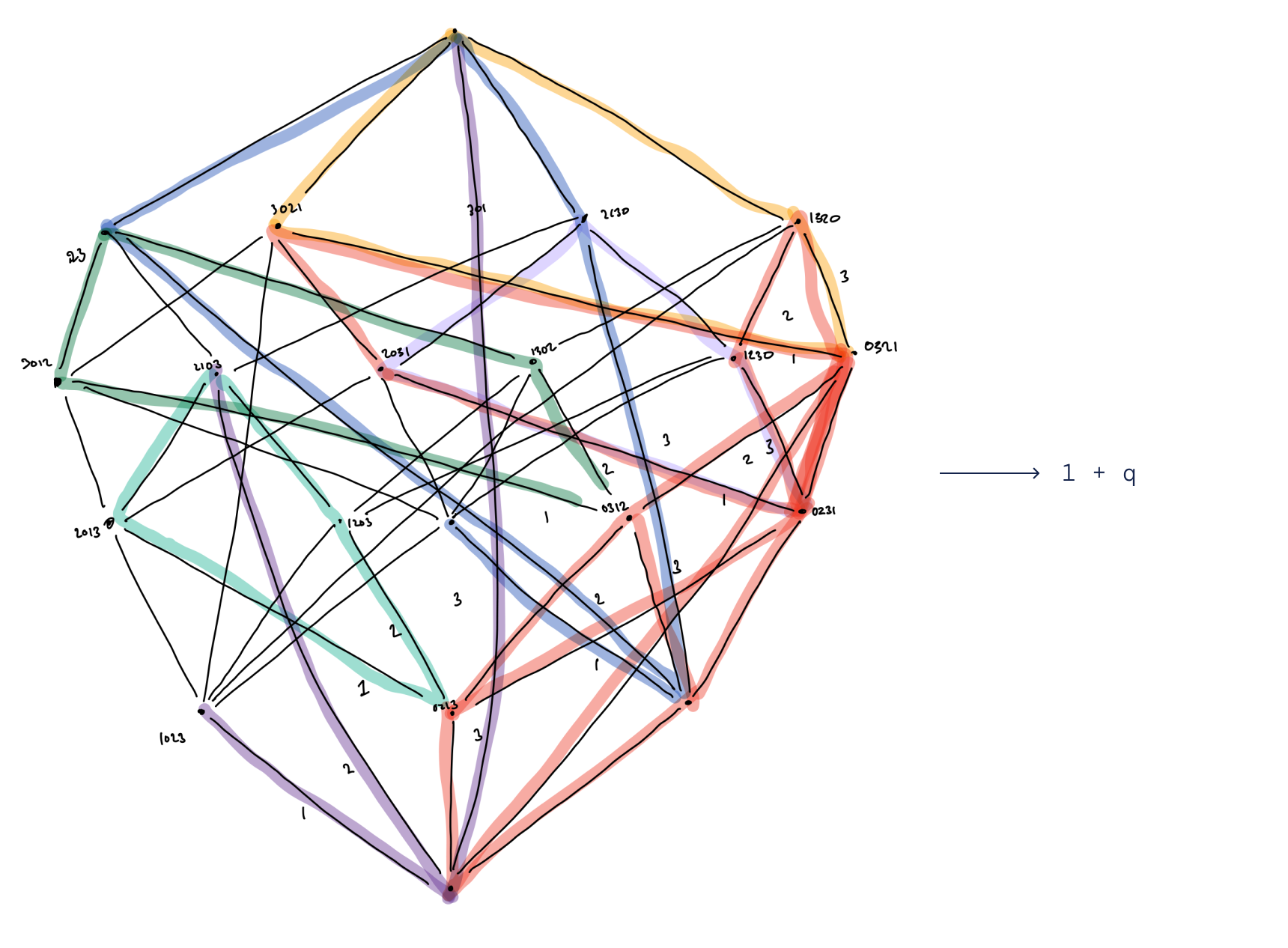
ウィリアムソン教授との共同研究では、MLを使用して表現論の長年の予想に新しいアプローチを発見するのに役立ちました。40年近く進展がなかった組合せ不変予想は、特定の有向グラフと多項式の間に関係が存在するはずだと述べています。MLの技術を使用することで、そのような関係が実際に存在することに自信を持ち、それが壊れた二面角間隔と極値反射という構造に関連している可能性があることを特定することができました。この知識を元に、ウィリアムソン教授は組合せ不変予想を解く驚くべき美しいアルゴリズムを予想することができました。私たちは、新しいアルゴリズムを300万以上の例で計算的に検証しました。

Professor LackenbyとProfessor Juhászと一緒に、私たちは結び目について探求しました。結び目は位相学の基本的な研究対象の一つであり、ロープが絡まるさまざまな方法だけでなく、量子場理論や非ユークリッド幾何学とも驚くほどの関連があります。代数、幾何学、量子論は、これらの対象に対して独自の視点を共有しており、これらの異なる分野がどのように関連しているのかという長年の謎があります。私たちは、そんなパターンを発見するためにMLモデルを訓練しました。驚くべきことに、これにより特定の代数的量である「シグネチャ」が結び目の幾何学と直接関連していることが明らかになりました。これはこれまでに知られていなかったし、既存の理論によって示唆されたものでもありませんでした。機械学習の属性解釈技術を使用して、私たちはProfessor Lackenbyに新しい量である「自然な傾斜」というものを発見する手助けをしました。これは今まで見落とされていた構造の重要な側面を示唆しています。そして私たちは一緒に、これらの異なる数学の分野の最初のつながりを証明することができました。

<img alt="私たちは、異なる数学的対象間の関係についてMLが光を当てることができるかどうかを調査しました。「ブルハット区間」とそれに関連する「カジダン・ルシュチク多項式」がここに示されています。ブルハット区間は、2つずつオブジェクトを交換することで、コレクションの順序を逆にするさまざまな方法を表す図です。KL多項式は、このグラフが高次元空間で存在する方法について、数学者に何か深く微妙なことを伝えます。興味深い構造は、ブルハット区間が100個以上、1000個以上の頂点を持つ場合にのみ現れ始めます。

<img alt="私たちのモデルは、私たちを驚くべき新しい数学的結果へと導いた以前に発見されていなかった構造をハイライトしています。ここには結び目の幾何学とシグネチャの驚くべき関係が示されています。結び目の幾何学は、正準的な方法で測定した場合の形状（たとえば、体積）に関連しています。シグネチャは、結び目が自分自身を交差させてねじれる様子を見ることで計算される代数的不変量です。

学習技術とAIシステムの使用は、数学におけるパターンの特定と発見に大きな可能性を秘めています。現代の機械学習が特定の種類のパターンを見逃すかもしれないとしても、私たちのNature論文がAIを純粋数学の有用なツールとして考える他の研究者にインスピレーションを与えることを願っています。結果を複製するためには、誰でも私たちのインタラクティブなノートブックにアクセスすることができます。ラマヌジャンの驚異的な思考力について考えると、ジョージ・フレデリック・ジェームズ・テンプルは「数学の大きな進歩は論理ではなく創造的な想像力によって達成された」と書きました。数学者と協力して、AIが人間の直感の美しさを新たな創造性のレベルに引き上げる方法を見ることを楽しみにしています。

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!