「対数正規分布の簡単な説明」
Explanation of the log-normal distribution
有名な正規分布のわずかな変更
背景
正規分布は特にデータサイエンスや機械学習の分野で有名ですが、対数正規分布は聞いたことがありますか?生物学からファイナンスまで幅広い産業で応用されるため、データサイエンティストにとって非常に重要な概念です。本記事では、この分布の理論と応用について詳しく探求します。
定義
対数正規分布は比較的理解しやすいです。ランダム変数Xが対数正規分布に属する場合、その対数が正規分布に従います:
以下のプロットはこの概念を視覚化しています:
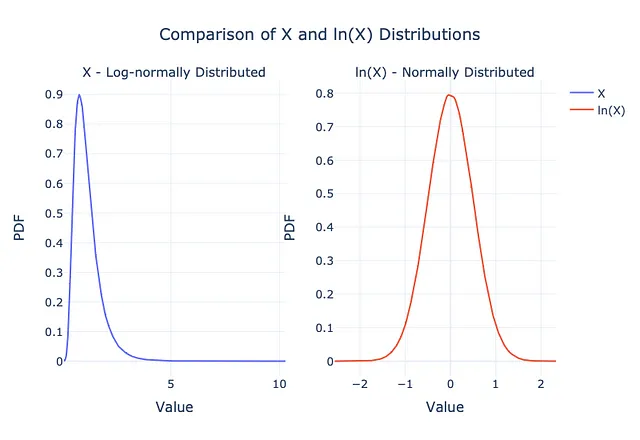
左側のプロットのランダム変数に対数を適用すると、右側の正規分布になることに注意してください。
理論
もしZが標準正規変数で、平均µが0、標準偏差σが1である場合、ランダム変数Xの対数正規分布は次のように表されます:
そして、方程式の両辺に対数を取ると:
右辺はZが正規分布に従うため、Xの対数が正規分布であることがわかります。
対数正規分布の確率密度関数(PDF)は正規分布に非常に似ていますが、ランダム変数xに対数変換が適用されます:
PDFの導出についてはこちらをご覧ください。
応用
対数正規分布は、サイズに依存しない成長率をモデル化するために頻繁に使用されます。以下は自然現象でよく見られる例です:
- 生物のサイズの測定
- 降水量の量
- 石油埋蔵量
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






