ローリング回帰による時間変動係数の推定

Estimation of Time-Varying Coefficients using Rolling Regression.

回帰係数の事前分布としてのガウシアンランダムウォーク

回帰分析において、説明変数と目的変数の関係が時間とともに変化する可能性を考慮することは、課題の一つです。

データサイエンスから計量経済学へ

度々、データサイエンティストは、ビジネスが仮定を持ち、モデルがそれが正しい可能性を組み込む必要があるシナリオに遭遇します。

バニラの回帰モデルは、E[Y|X]を推定するのに優れています。Xᵢの係数（またはβᵢ）は、Xᵢが1増加したときのYの増分の変化として解釈することができます。計量経済学では、βᵢは時間とともに変化するという仮説がしばしば立てられ、それをβᵢₜと呼ぶことができます。実際に推定しようとしているのは、E[Y|X,Time]です。以下は、ある会社の2年間の収益のチャートです – 季節性のある事業であり、βも時間に依存している理由はありません。

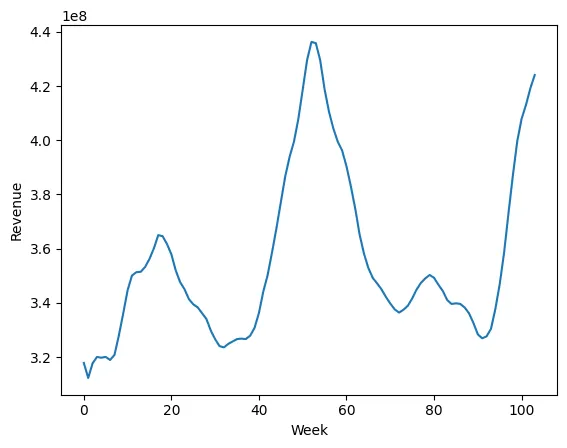
この投稿では、回帰分析における時間変動係数の概念を紹介し、マーケティングミックスモデルに適用する方法を示します。まだご覧になっていない場合は、ゼロからMMMを構築するVoAGIシリーズと、それに関連する要素をご覧ください。マーケティングミックスモデルは、広告、価格設定、プロモーションなどの異なるマーケティング活動が売上やその他の結果に与える影響をマーケターが測定するための統計ツールです。典型的なマーケティングミックスモデルは次のように表現できます：

• データパイプラインのテスト計画を進化させる
• A/Bテストの意味を理解する：厳しい質問でよりよく理解する
• JavaScriptを使用してOracleデータベース内からHugging Face AIを呼び出す方法

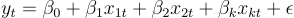
ここで、yₜはt時点での結果変数（例：売上）であり、xᵢₜはt時点での予測変数（例：広告費、価格など）であり、βᵢは各予測変数の結果変数への影響を測定する係数であり、Ɛₜは誤差項です。

ただし、このモデルでは、係数が時間によらず一定であると仮定しており、これは場合によっては現実的ではありません。例えば、広告の売上への影響は季節性、製品の寿命サイクル、競争環境などによって異なる場合があります。この変動を捉えるために、回帰分析で時間変動係数を使用することができます。これにより、係数を他のいくつかの変数の関数として時間とともに変化させることができます。例えば、次のように記述することができます：

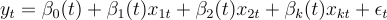
ここで、βᵢ(t)は時間または係数のダイナミクスを捉える他の変数の関数です。これらの関数を指定する方法は、データの性質や研究の問いによって異なります。

ガウシアンランダムウォーク

メディアの有効性が時間とともに変化する場合、係数として時間変動関数で捉えることができます。最も一般的な選択肢の一つは、ガウシアンランダムウォークです。

これは、株式や金などの金融データのモデリングに使用されるプロセスです。

ガウシアンランダムウォークは、独立かつ同一分布の確率変数の累積効果をモデル化する確率過程です。また、正規ランダムウォークまたはウィーナー過程とも呼ばれます。ガウシアンランダムウォークは、以下のようなランダム変数の系列 X₁、X₂、…、Xₙ によって表されます。ここで、各 Xᵢ は平均0、分散1の正規分布に従い、最初の3つの変数の合計

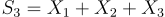
ランダムウォーカーの位置は時間nである。ガウスランダムウォークには、マルコフ過程であること、定常な増加を持つこと、確率的に連続することなど、いくつかの重要な特性があります。

ベイジアン時変MMMのコード

この記事で構築したPyMCモデルのアップグレードバージョンです。週ごと、四半期ごと、学期ごと、年ごとに係数を変動させるためのコードを追加しました。この形式の回帰は、ローリング回帰とも呼ばれます。

コードの変更点を見てみましょう。

まず、このモデルがBayesianMMMという関数にラップされていることに気付くでしょう。これは便利のためで、異なる引数で実行できるようにするためです。 この例では、splitsという1つの引数を受け取ります。これは、時間の定義がどれだけ細かいかを決定するものです – 週ごと（W）、四半期ごと（Q）、半年ごと（H）、または年ごと（YoY）です。

また、PyMCモデル自体はcoordsという引数を受け取ります。これは基本的には時間変数です。週ごとに係数を変化させる場合、時間変数は1…104になります。四半期ごとに変化させる場合、1,1,1…,2,2,2…,3,3,3…,4,4,4…,1,1,1…となります（これは2年間のデータです）。

次に、係数はTruncatedNormalではなくGaussianRandomWalk変数になっています。以前と同様に、事前分布の位置で初期化されます（これを思い出せない場合は、こちらに戻ってください）。 このセットアップでは、各時間期間には独自の係数がありますが、係数は連続する時間期間で情報を共有します。 これがローリング回帰の最大の強みです。

さて、3つのケーススタディを見てみましょう。

ケーススタディ1 – 上流層におけるメディア戦略の時間変化はどのようになりましたか？

上流層のマーケティングは、まだ購入に至っていない潜在的な顧客の認識と関心を喚起する活動を指します。これは直接的には変換や販売につながらないため、測定が難しいですが、顧客の旅路に微妙かつ長期的に影響を与えます。ただし、どのチャネルが効果的か、時間の経過に伴うトレンドを把握しておくことは役立ちます。

非常に有益な知識が得られました。時間の開始時点では、ダイレクトメールは長い間最も性能が低かったチャネルでしたが、後にテレビを上回りました。テレビの効果は、CTVの登場とともに時間とともに低下しているという傍証があります。

また、CTVが時間とともにEmailを上回っていることも観察されます。これらは興味深い観察ですが、A/Bテストなしでは結論を導くことはできません。

ケーススタディ2 – 私のビジネスは季節的で、最も収益があるのはホリデーシーズンです。

マーケターは、有料検索の効果が一年を通じて一定であるとは思わず、四半期の変動や機会に応じてキャンペーンを調整する必要があります。ただし、特に小売業やeコマース業界では、一般的なトレンドが観察できる場合があります。

有料検索の効果は、特にホリデーシーズンには第4四半期に高くなります。オンラインショッピングの活動が増加し、消費者が割引、特売、またはギフトのアイデアを提供する広告をクリックしやすくなるためです。逆に、消費者の需要が低下し、広告主が変換率の低下とクリックごとのコストの上昇に直面する第1四半期には、有料検索の効果が低下する可能性があります。第2四半期と第3四半期は、特定の業界や市場条件に応じて、より安定したまたは穏やかな結果を示す場合があります。

有料検索の効果は、第4四半期において最も高いことが予想されます。

ケーススタディ3 – メディアの効果の年々のトレンドを測定したいです。

年度対比のトレンドは、1年から次の年にかけての主要なパフォーマンス指標（KPI）の変化です。これにより、マーケターは現実的な目標を設定し、予算を調整し、うまくいくものとそうでないものに基づいて戦術を最適化することができます。

過去のデータの分析、市場調査の実施、さまざまな戦略のテストにより、マーケターは有料検索の効果を最適化し、四半期ごとに目標を達成することができます。パブリッシャーのガイダンスや社内のA/Bテストによって、ROIが最も高い時期も特定できます。最後に、これらすべてが私たちのMMMの調整に役立ちます。

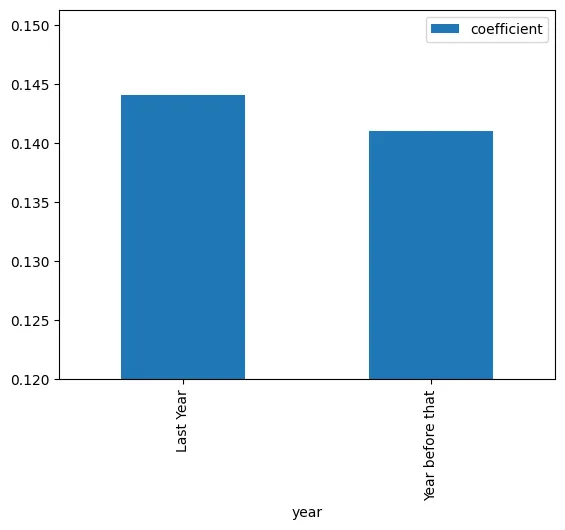
YoYの有料検索の効果は、おおよそ2%改善されていることがわかります。このようなトレンドは非常に頻繁に報告され、マーケティング部門の成功によるものとされています。

結論

私のMMMシリーズに従ってくれた場合、MMM（または他の測定）が利害関係者にとって消化しやすいことの重要性を強調しました。時間変動係数は、バニラのMMMに投げかけられる多くの質問に答えるのに役立ちます。ベイズ最適化技術を用いることで、モデルコードに小さな調整を加えることができ、それによってこれらの質問に本質的に答えることができます。

回帰における時間変動係数の利点の一つは、予測変数の効果が時間とともにどのように変化するかをより正確かつ柔軟に推定できることです。また、これらの効果がいつ、どのように変化するのか、そしてこれらの変化を引き起こす要因は何かを特定するのにも役立ちます。これにより、マーケターはより効果的かつ効率的なマーケティング戦略を設計し、マーケティングミックスを最適化することができます。

読んでくれてありがとう 😊

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!