「Maxflow Mincut定理の発見：包括的かつ形式的なアプローチ」

Discovery of the Maxflow Mincut Theorem Comprehensive and Formal Approach

フローネットワークと最大流最小カット定理の探求

導入

ネットワークフロー最適化の領域では、最大流最小カット定理は顕著な数学的なマイルストーンとして際立っています。その優雅さは、流体やリソースのネットワークを介した流れに関連する複雑な最適化問題を解く鍵です。その応用範囲は、効率的なフロー管理が重要な輸送ネットワークから通信インフラに至るまで、さまざまなシステムに及びます。この定理とその数学的な表現の背後にある基本的な概念を理解することで、さまざまな実践的なシナリオでリソースの利用を最大化し、最適なパフォーマンスを達成するための謎を解くことができます。

本記事では、この定理をすべての読者にわかりやすくすることを目指します。私たちは、その歴史的な発展について説明し、この定理とその数学的な研究領域全体の基礎的な概念を示す初期の定式化からのルーツを概説し、この定理とその実世界への応用に深く入り込みます。効率的な輸送システムの設計から画像処理の課題に取り組むまで、その多様性は限りがありません。実際の応用を探求することで、この定理がさまざまな分野や産業に与える深い影響を目の当たりにすることができます。

最後に、簡単さと形式を兼ね備えた包括的な説明を提供することが目標です。高度な数学の事前の専門知識は必要ありませんが、グラフ理論と離散数学（論理と集合論）の一部の知識は非常に役立ちます。好奇心とこの特別な定理の有用性を解き明かす意欲があれば、それだけで十分です。

歴史

最大流最小カット定理は、FordとFulkersonによって1956年に最初に紹介されました。彼らの画期的な論文「ネットワークを通る最大の流れ」には、情報理論の発展に貢献したClaude Shannonなどの関連する数学者も協力しています。この定理は、ネットワーク内の最大の流れがカットの最小容量と等しいことを述べています。ここで、カットはネットワークのノードを2つの互いに素な集合に分割するもので、その容量はカットを横切るすべてのエッジの容量の合計です。それ以来、この定理はフローネットワーク理論の基石となっています。

• 「iOSのための10の最高のデータ復旧ツール（2023年8月）」
• 「ビジネスはマルチリンガル製品分類器の精度をどのように改善できるのか？このAI論文では、訓練データが限られた言語における分類精度を高めるためのアクティブラーニング手法であるLAMMを提案しています」
• オブジェクト指向データサイエンス：コードのリファクタリング

ただし、この定理の導入には、他の重要な科学的貢献が伴います。たとえば、Edmonds-Karp、Ford-Fulkerson、Dinicのアルゴリズムなどがあります。これらはすべて、ソースとシンクを持つネットワークを通過できる最大のフローを見つける共通のタスクを果たします。同様に、最大流最小カット定理を利用することで、この値はソースとシンクを分ける最小カットと一致します。さらに、アルゴリズムの内部計算を利用して、最小カットを構成するエッジの集合を特定することもできます。

フローネットワーク

したがって、以下の定理の説明を簡略化するために、まずグラフ理論のフローネットワークの基礎的な概念を知る必要があります。

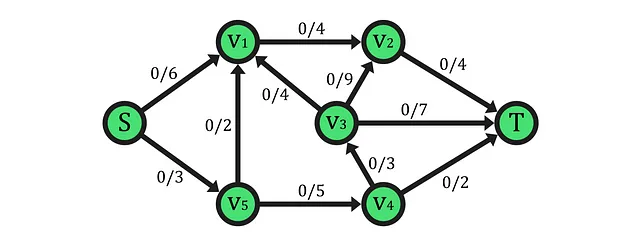
上記の例のように、フローネットワークは、リソース（フロー）の一定量を「ソース」（Sノードで表される）から「シンク」 （Tノード）へ伝達または移動する必要があるネットワーク構造化されたオブジェクトまたはシステムを表す重み付きの有向多重グラフです。ただし、この特定の例では、ノード間には1つのエッジしかありませんので、多重グラフの特性は表示されていません。

このようなテンプレートの表現を実現するために、フローネットワークには各エッジに関連付けられた重みがあります。この文脈では、重み付きエッジはリソース（フロー）交換のいくつかのポイント間の物理的/論理的な接続をモデル化し、重みの実際の正の値はその容量（サポートされる最大フロー）を表します。上記の例では、エッジラベルの右側に容量が示されており、この場合は現在のフローは0です。

各エッジの容量に加えて、リソースが単位時間あたりに各エッジを通過する速度を定義する重要な指標はフローです。これは道路上の交通やパイプラインを通る水の量と考えることができます。したがって、ネットワークのソースがすべてマスターソースフロージェネレータに接続されている場合はソースノードまたはスーパーソースノードで生成され、同様の構造がシンクに存在する場合はシンクノードまたはスーパーシンクに取られます。したがって、エッジ(u,v)（グラフのエッジ集合Eに属する）を入力とし、その現在の時間f(u,v)でのフロー（正の実数値）を出力する関数f:E→Rでフローを定義できます。

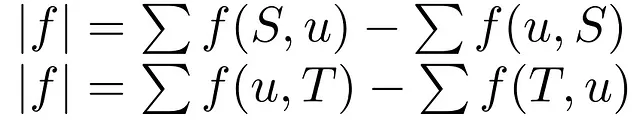
したがって、フローネットワークの対応するソースSまたはシンクTのすべての上記の式を計算すると、グラフを通過する総フロー量を得ることができます。

フローがネットワークの制約に適合することを保証するために、次の2つの基本的な特性を満たす必要があります：

1. 容量制約：エッジを通過するフローはその容量を超えることはできません。形式的には、エッジの容量を「c(u,v)」と表し、そのエッジを通過するフローを「f(u,v)」と表すと、すべてのネットワーク内のエッジ(u,v)に対して0 ≤ f(u,v) ≤ c(u,v)という条件を満たす必要があります。つまり、エッジの容量が設定する以上のフローは通せないということです。
2. フロー保存：ソースノードとシンクノードを除くすべてのノードで、ノードに入る合計フローはノードから出る合計フローと等しくなる必要があります。

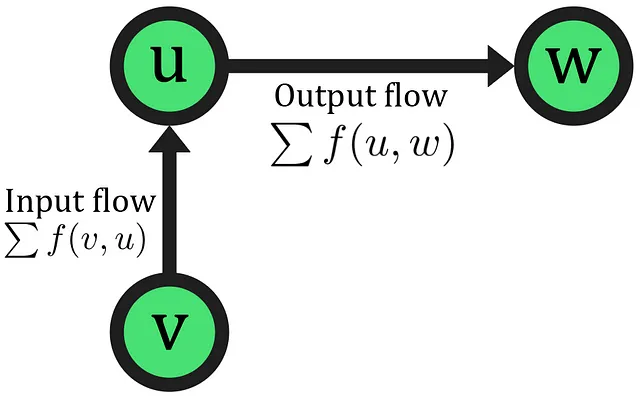
これにより、フローは中断することなく続き、ネットワーク内で蓄積または消散することはありません。ただし、システムにフローの蓄積が必要な場合は許可できます。数学的には、ノード「u」とその隣接ノード（スーパーノード「v」および「w」によって表される）に対して、フロー保存特性は以下のように表されます：

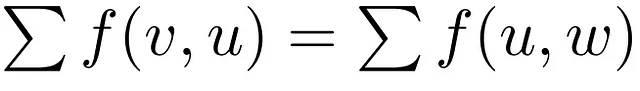
最後に、フローは互いに打ち消すことができることに注意してください。つまり、ノードuとvの間にフローf1(u,v)とf2(v,u)が存在する場合、f1(u,v)を減少させることはf2(v,u)を増加させることと同等です。

残余ネットワークと増加パス

ここでは、以前に説明したアルゴリズムを使用して最大フローを見つけるのに非常に役立つ2つの新しい、より洗練された概念を紹介します。

これらのうち最初の概念は、与えられた時点でのエッジの容量とフローの差である残余容量です。これを次のように定義します：

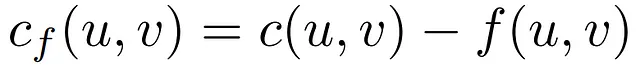
この特性を考慮して、標準的なネットワークとの唯一の違いがエッジの再定義された容量である残余ネットワークと呼ばれる特定のタイプのフローネットワークを定義することができます。残余ネットワークは、エッジの対応する残余容量にマップする関数cfを備えています。

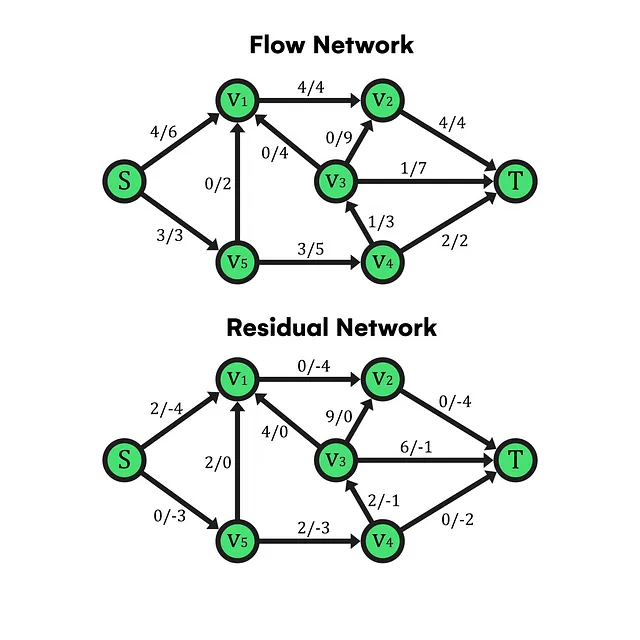
この例では、上のグラフのすべてのエッジに特定のフロー関数が存在するネットワークがあります。したがって、残余ネットワークは以下のようになり、エッジのラベルには対応するエッジの方向に応じて送信可能な残余容量と流れを元にした逆方向の流れを元に戻す場合に配信できる量が含まれています（ネットワークに対称性がある場合に有用となる流れのキャンセルプロパティを思い出してください）。

ここでは、ネットワークを通じて達成されたフローは、前述のようにソースまたはシンクの式で計算できます。この場合、ソースからの出力が4+3ユニットのSまたは4+1+2ユニットのTに均等に分布される7ユニットのフローです。ただし、逆（または双方向）で(v5, v1)エッジを考慮すると、S-V1-V5-V4-V3-Tというパスに沿ってさらに2ユニットのフローを送信する可能性があります。これにより、合計フロー量が増加し、与えられたネットワークで利用可能な最大のフローになります。その後、残余ネットワークを導出した後、ソースとシンクを接続する1つ以上のパスにおいて、すべてのエッジの残余容量が0よりも大きい場合がある可能性があります。言い換えると、複数のソースやシンクが存在する場合に、ソースからシンクへのフローを輸送することができるパスが存在するということです。

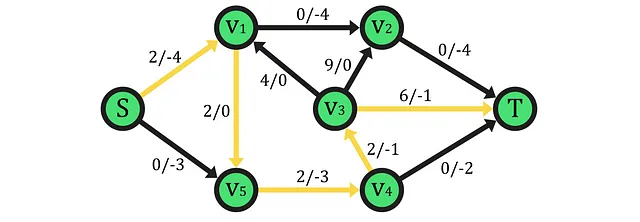
この文脈では、このようなパスは、フローの最大化またはコストの最小化の問題を解決するために使用されるアルゴリズムの基盤となり、増加パスと呼ばれています。上記のネットワークでは、確立されたフローにより、SからTへ2ユニットのフローを輸送する増加パスが存在することがわかります。したがって、ネットワーク上の実際のフロー関数は、それを通じて輸送可能な最大フローを提供しないため、後で説明する最大フロー最小カット定理が直面する問題の一つです。

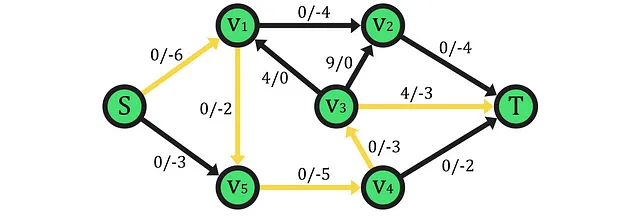
その結果、表示されたパスを通じてフローを増やすと、ネットワークフローを増加させる他のパスはないため、結果的なフローは9ユニットで最大となります。最後に、ネットワークの最大フローを見つけるためには、フォード・ファルカーソンなどのアルゴリズムが使用されますが、これらはフローが全くない残余ネットワークから始まり、増加パスを見つけながら（残余エッジや逆方向フローの助けを借りて）フローを増やしていく直感的な手順(貪欲法)を使用します。したがって、増加パスを増やすことができない場合、到達したフローが最大であることが保証されます。つまり、いくつかのエッジのキャパシティ不足やネットワーク内のエッジ不足による、より速い方法でリソースをSからTに移動する方法が存在しないことを示します。

この手順を考える別の方法は、反復ごとに追加されるフローの量を考慮することです。任意の増加パスに対して、追加できる最大の量は、残余容量が最も少ないエッジによって与えられます。なぜなら、それがSからのフローのボトルネックとなるからです。フローの全ポテンシャルに制限をかける能力を持つボトルネックエッジは、フローを最大化する必要がある状況で重要です。

例えば、上部のシンプルなフローネットワーク（残余）を考えます。ここには利用可能な増加経路が1つしかないため、エッジ(v2, v3)のボトルネックコンポーネントを明確に特定することができます。このエッジの最大フローは全体のパス（そしてこの場合はネットワーク全体）の最大フローを3に設定します。パスに示されているようにフローを3単位増やした後、フローをさらに増やすための増加経路は存在しないため、最大フローは達成されたと結論付けられます。しかし、結果のフローの検証を確実にする別の方法は、ネットワーク内のボトルネックに焦点を当てることです。つまり、SとTの間のすべてのパスがボトルネックの値がゼロである、つまり、最大残余容量が0であることと同等であり、これは増加経路の存在しないことと同じです。これ以上フローを追加することはできず、現在のフローは上記のように最大と見なされます。

ボトルネックに関する疑問を解決するためには、最大フローはFord-Fulkersonのようなアルゴリズムを介して最大フローを見つけるために使用されるすべての増加経路のボトルネックの合計としても表現されることを強調しておきましょう。各パスは、それに対応するボトルネックによって決定されるだけのフローを追加します。

フローネットワークのカット

フローネットワークの基礎に関するカバーする最後の部分はカットです。これはMaxflow Mincutの定理の基本的な要素であり、ネットワークのボトルネックと分割の関係など、前のセクションを理解するための重要な概念です。

まず、定義から始めましょう。カットは、ソースノードSが1つのセットAにあり、シンクTが前のセットと互いに素な別のセットBにあるネットワークノードの分割です。

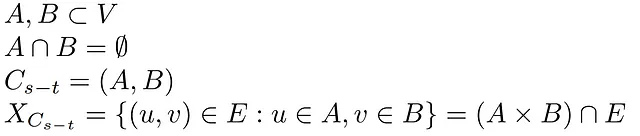
AセットもBセットも空ではないため、それぞれソース（複数）とシンクを含む必要があります。したがって、ネットワークが接続されている場合、AとBのノード間の接続機能を果たすエッジが双方向に存在します。また、これらのエッジはカットセットと呼ばれる別のセットに含まれていますが、Aのノードを起点としBで終わるエッジのみが考慮されます。つまり、正しい方向にフローを輸送できるエッジです。

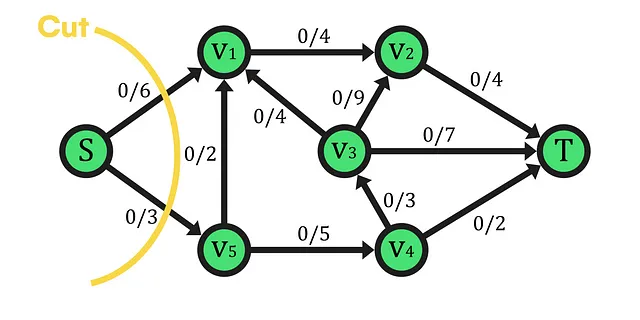
例えば、上記のグラフに適用できる最も単純なカットを見ると、頂点集合Vの分割がA={S}とB={V1,V2,V3,V4,V5,T}の集合の和となります。唯一のネットワークソースが1つのセットに孤立しているため、カットの概念とその後の特性をより正確に理解することができます。通常、カットはAまたはBのいずれかを囲むように示される直線として表されます。さらに、区切りの境界線は、カットセットに属する複数のエッジを両方向に横断します。これらのエッジは、ネットワークの任意のカットとフローの関係を確立する際に重要な役割を果たすフローと容量を決定するために使用されます。これは、この記事で提示されている定理を証明する上で重要です。

一方、与えられたカットを通過するフローは、A-B方向にフローを運ぶすべてのエッジの合計から、BからAへの逆方向のフローを引いたものとして定義されます。

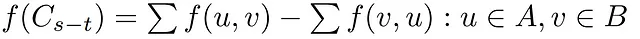
しかし、この文脈ではフローは重要な値ではありません。なぜなら、フローはカットの容量に制約されているからです。このため、フローと同様にカットの容量も同様に定義することができます。ただし、上記の式の最初の項目のみを考慮に入れます。つまり、SからTにフローを運ぶことができるエッジの容量を引く必要はありません。

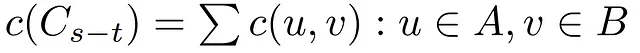
フローと容量の概念をカットで形式的に提示した後は、これらのアイデアをできるだけ簡単にし、この領域での理論を理解するために、いくつかの例を考慮する必要があります。

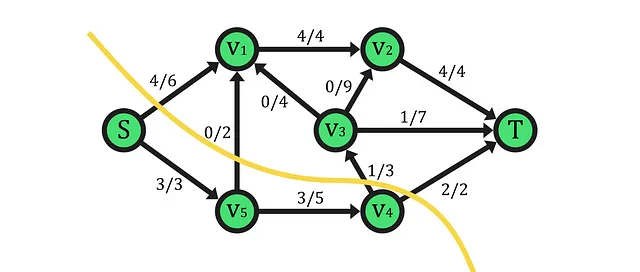
まず、各セットの頂点を調べてみましょう。セットA={S,V5,V4}とB={V1,V2,V3,T}を残します。ネットワークに既にフローが割り当てられているため、カットフローはゼロではなく、セットAからBに接続されたエッジ上のフローの合計によって決定されます。

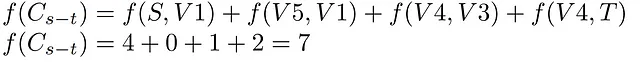
さらに、その容量は同じ前のエッジとそれぞれの容量から得られ、カットを通過することができる最大のフローを構成します。

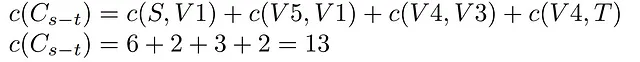
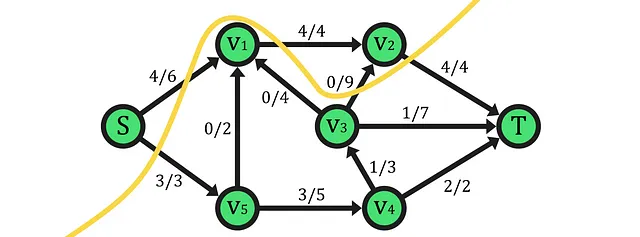
この興味深い最後のサンプルカットでは、カットが両方のセットの頂点が接続された成分である必要はないことがわかります。つまり、基本的なカットの制約を満たす限り、各セットには任意のノードを含めることができます。

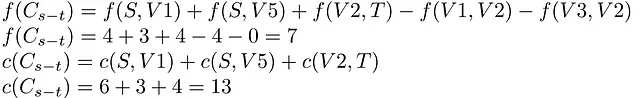
また、この例はカットとフローの関係を理解する上で特に役立ちます。まず、カットの定義によれば、カット後のネットワークはs-tに関して切断されていることに注意してください。つまり、そのカットの容量は、ソースアセンブリからシンクへのすべてのエッジの合計として計算されます。フローの単一のソースを分離する最も基本的な場合では、カットの容量はネットワークの最大フローを超えるか等しくなります。しかし、前の例では、より多くの出力エッジを持つノードを挿入することで、カットの容量が必然的に増加することが分かります。つまり、最大フローに到達するために必要なエッジよりも多くのエッジが存在するため、ソースのエッジが瓶の首の場合、その後にネットワークを通過するフローを決定します。

定理の主張

フローネットワークの最適化の課題に取り組む主な目的は、ソースからシンクへ伝えることができる最大のフローを決定することです。これは、容量、フロー保存の制約に従い、達成されたフローが実際に最大であることを確認しながら達成する必要があります。したがって、定理に取り組む際には、その値をフローやそれに類似して大まかに計算する上限で制約するステップを踏むことになります。

まず、そのような上限が最も容量の少ないカットであることを強調しておきます。定理の主要な補題として、完全に理解されるわけではないかもしれませんので、2つのより単純なアイデアを紹介して証明しましょう。

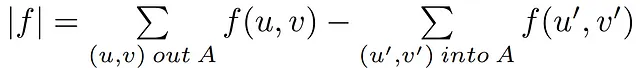
最初のものは、任意のカットを通るフローと総ネットワークフローの等しさを証明することを含みます。これは、ソースから生成されるフローと一致します。この目的のために、カットの集合Aに対して帰納法を適用しながら、初期の命題を真と仮定し、A={S}を基本ケースとして使用し、SまたはTとは異なるノードに対してフロー保存の原則を使用します。ただし、これを詳細に説明するのは複雑になるため、より簡単で非常に似たアプローチを選択します。

前の証明の過程でのフロー値には、許容される任意の値があり得ることに注意してください。

1- フローの定義： 初めのステップでは、ネットワーク内の任意のフロー関数fの総フロー値とその可能な定義の1つから始めます。ここでは、ネットワークカットのための最小の可能な集合AであるソースノードSを参照として、フローの値をSによって生成されるフローからSへの流入フローを引いたものと一致させます。なぜなら、時にはSに戻る一定量のフローが存在する場合があるからです。

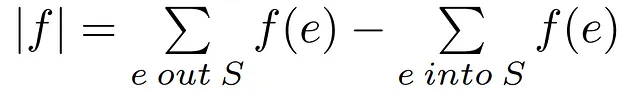
2- フロー保存の性質： ネットワークフローをソースSによって生成される総フローとみなした後、全てのノード（S-Tを除く）は受け取ったフローを伝播させるフロー保存の原則を適用し、出力フローから入力フローを引いて|f|に寄与するフローをゼロにします。次に、任意のカット(A,B)を取ると、フローを生成するノードvを除く集合A内のノードによる総フローはゼロとなり、前述の等式を満たします。

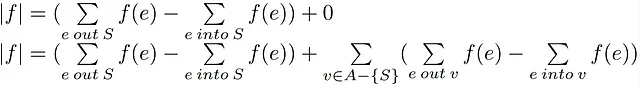
3- カットを通るフロー： 最後に、第2項においてAのノードからの出力フローと最初の項におけるS自身の出力フローを合計し、前のノードからの対応する入力部分を引いた式に到達します。これは先述のカットフローの定義に対応し、したがってネットワークを通るすべての既存のフローが任意のカットを通るフローと一致することが結論されます。

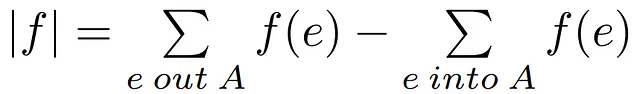
最大フローミンカット定理に関する証明に含まれる2番目の命題は、ネットワーク内の任意のフローの値を任意のカットの容量値で上限に制約する不等式です。

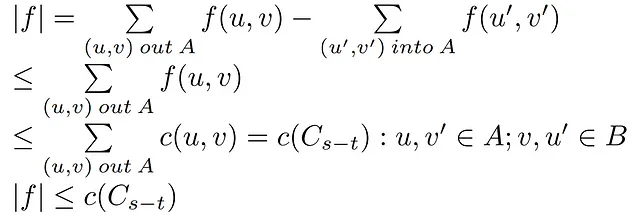
1- 代替フローの定義： カットのフローに関する前の結果を使用して、任意のフロー|f|を任意のカット(A,B)を通るフローと等しくすることができます。

2/3- フローの境界： 2番目のステップでは、集合AからBへのフローを持つエッジの出力フローのみを残し、集合A内の入力フローをモデル化する2番目の項を除外する不等式を確立します。このような項を除去すると、残りのエッジの合計フローが減少しない限り、結果は常に前の結果以上になります。

その後、Aからの出力エッジのフローがそれらのエッジの容量以下であるように不等式の値を増やすことができます。この不等式の妥当性は、すべてのネットワークエッジに現れる容量制約によって与えられます。

4- 弱双対性： 集合Aのすべての出力エッジの容量の合計をカット容量の定義によって一致させると、ネットワーク内の任意のフローとカットについて、フローは常にカット容量以下であるか、等しいことが結論づけられます。これは、証明しようとしている定理の出発点となります。また、フローを最大化しようとすると、カット容量を最小化することで達成できる点に達します。これにより、最大フローと等しい最小容量カットが常に存在するという確実性のない弱双対関係が確立されます。

この段階で、最大フロー最小カットの定理の弱二重性に到達した後、より理解しやすく検証可能な文を提供できます。

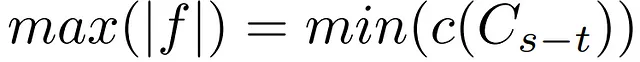
すでに述べたように、定理は強二重性を介して成立し、任意のネットワークの最大フローは最小容量カットに一致します。前の弱二重結果とは対照的に、この定理はフローの最大化の二重が任意のカット容量の最小化と完全に等しいことを保証し、二つの結果の間の差異の可能性を除去し、補題に強い二重条件を与えます。

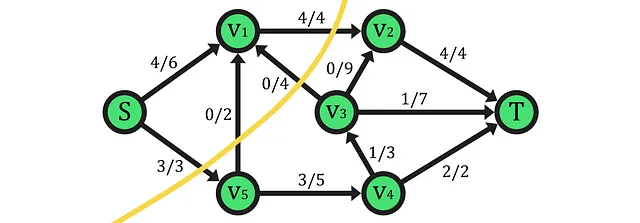
その証明に進む前に、この定理の使用例を強調しておきましょう。ここでは、最大フローの値が7であり、それは各出力カットエッジの容量の合計に等しいことに注意してください。これらのエッジは最大容量でフローを運びますが、最小容量カットなどでは、これらのエッジがボトルネックとなります。つまり、カットセット自体がグローバルネットワークフローのボトルネックとして機能します。このアイデアを簡潔に説明するために、以下にそれを理解するのに役立つリソースがあります：

最大フロー最小カット定理の直感的な説明は何ですか？

最大ネットワークフロー問題を解決するのに役立つ、最大フロー最小カット定理の証明を読もうとしています。…

math.stackexchange.com

証明

ネットワークの最大フローが、すべての場合においてネットワークの最小容量カットと等しいことを証明したい場合、定理が真であるためには等価である必要がある3つの命題を使用します。

カット (A, B) が |f|= cap(A, B) を満たす。

フロー値 |f| が最大である。

フローネットワークに拡張可能なパスが存在しない。

すべての文が等価であることを示すために、論理的な含意 1⇒2⇒3⇒1 を証明します。つまり、どの文からも他の文を推論できることを意味します。 1⇒2 の場合、先に示した弱二重性を使用して簡単に検証できます。次に、任意のフローが最小容量のカットよりも小さいことを考慮すると、任意のカットの容量に等しいフローが存在すると仮定すると (1)、弱二重性から、この容量が任意のフローの上界であるため、結果として生じるフローは、その上界と一致し、最大限 (2) です。

2⇒3 で進めるには、反証 ¬3⇒¬2 を取ることが最も簡単な方法です。したがって、例として任意のフロー |f| を取ると、拡張可能なパスs-t ¬(3) がフローネットワークでフローを輸送できる場合、|f| は対応するパスを通じて増加させることができ、したがって |f| は元々最大フローでなかった ¬(2) となります。

最後に、この証明で最も難しいステップは 3⇒1 です。まず、フロー |f| が拡張可能なパスを持たないネットワークを仮定します。さらに、残余ネットワークで S から到達可能なすべての頂点を含む集合 A を定義します。つまり、残余ネットワークにおいて S から A へのパスが存在し、かつそのパスのすべての残余エッジがゼロでない頂点を含みます。これらの定義により、S が A に含まれることが確定しています。自己到達可能であるため、そして拡張可能なパスがないため、T は S から残余ネットワークで到達不可能であるため、少なくとも1つのノード (T) が集合 A に含まれていないことがわかります。その後、別の集合 B に T を挿入すると、ペア (A, B) がネットワークの有効なカットのすべての基準を満たします。

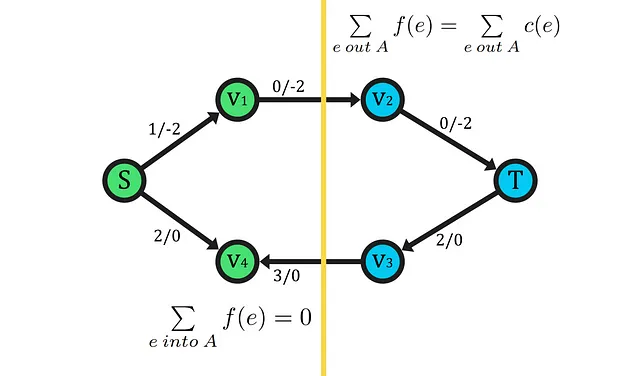
この時点で、カット(A, B)について2つのことを認識する必要があります。一方で、カットをS-T方向に流れるフローはその容量と等しくなければなりません。なぜなら、前の定義と仮定（3）により、フローが容量に達しない可能性があるのはBのノードが到達可能である場合のみです。したがって、カットエッジ上のフローが完全な容量に達しないことを引き起こすため、ノードはBではなくAの中になければならず、これは矛盾です。他方で、カットの他方向のフローは前と同じ理由でゼロになります。つまり、ゼロでない場合、残余ネットワークにはA-B方向（負符号で表される残余エッジフロー）のエッジが存在し、Bのノードに到達して矛盾を引き起こします。

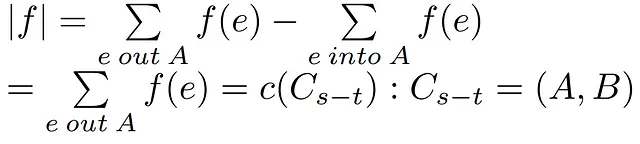
最後に、ネットワークフローをカットフローに一致させ、前に示したように、フローのカットへの項を削除し、フロー|f|が結果のカット容量（3⇒1）と等しいことを示すためにカット容量の定義を使用するだけです。

応用

最大フロー最小カット定理は、さまざまな分野で数多くの応用があります。しかし、短くするために、使用例の基本的な側面と正しく理解するためのより詳細なリソースを簡単に紹介します。

Ford-Fulkerson/Edmonds-Karpアルゴリズム

最初の結果として、定理によって提供される結果と結合したもの、例えば整数性定理といった他の結果との組み合わせにより、最大フローを計算するための一連のアルゴリズムの正当性証明がされます。

最も重要なものは、すでに説明したFord Fulkersonのアルゴリズムで、s-t増加パスを探索してフローを増加させる貪欲なアプローチです。しかし、このアルゴリズムの基本バージョンは、特定の入力（実数または無理数とその表現を使用する場合など）において、特定の状況で最大フローに終了または収束する保証がないため、増加パスの選択方法によります。これはまた、その時間計算量に影響を与え、最悪の場合、アルゴリズムが到達する最大フローの各（少なくとも1つの）単位ごとに、ネットワークのすべてのエッジをトラバースする必要があります（O(|E| |f|)）。

その後、この種の問題を解決するために最初に作成された前のバージョンを改善するために、増加パスの計算方法が改善されました。つまり、Ford-Fulkersonバージョンは深さ優先探索（DFS）を使用してTまでのランダムなパスを計算する一方、改良されたEdmonds-Karpバリアントは幅優先探索（BFS）アルゴリズムを使用して増加パスを見つけます。したがって、各反復で可能な限りエッジ数が少ない増加パスを選択することを目指して、前のバージョンに比べて終了保証があり、時間計算量がO(V E²)のオーダーで変更されます。

ただし、これらや類似のアルゴリズムを使用すると、ネットワークの最大フローだけでなく、容量がその値と等しい最小カットも計算できます。手順は非常に簡単です。ネットワークのすべてのエッジで最大フローを計算した後、最大フローミンカット定理に従って、残余ネットワークでSから到達可能なノードがカットのセットAを形成し、残りのノードがBとなり、結果として得られる最小容量カット(A, B)につながります。

最後に、最大フロー・アルゴリズムの研究領域は、ここに示されているものよりもはるかに広いことに注意しておく必要があります。したがって、学習を続けたい場合、以下のリソースにはこれらのアルゴリズムについて詳細に取り上げられています。

実用例

私たちの生活で相互作用するほとんどのシステムは、フローネットワークによって少なくとも一部モデル化することができるため、複雑なスケーラビリティの問題に対処するための重要なツールとなります。同様に、可能性は広範囲にわたるため、ここでは基本的な概念と直接関係のあるいくつかの事例のみを紹介します。

まず、道路ネットワークや公共交通システムから航空路線や貨物配送まで、すべての交通システムはフローネットワークとして表現することができます。その結果、交通パターンを分析し、ルートを最適化し、全体的な効率を向上させることができます。これは都市計画において特に重要であり、人々や車両、商品の流れを管理することは渋滞を防ぎ、スムーズな運営を確保するために不可欠です。さらに、これらの事例のすべてが完全に有益なものではありません。たとえば、フローネットワークは国の鉄道システムをモデル化することもできますが、軍事的な紛争の場合には、戦略的に最適な攻撃対象となる可能性があります。この特定の応用については、以下のリソースで詳しく学ぶことができます。

通信、エネルギー分配、さらには医療など、他の重要な実装にもかかわらず、私たちはコンピュータサイエンスとより密接に関連しているものに焦点を当てます。具体的には、コンピュータビジョンの分野と特に関連している、重要なブレイクスルーを達成している画像セグメンテーションアルゴリズムに重点を置きます。これは、画像をオブジェクト、被写体、または人間の目では区別できない領域に分割するためのアルゴリズムであり、フローネットワークはピクセル間の類似性/非類似性の尤度値のフローをエッジとして表現することで、その威力を発揮します。さらに、学習、生成、または分類の特定のタスクを最適化するためにフローの概念を使用する機械学習モデルなど、類似する範囲での応用も言及する価値があります。

結論

この記事では、フローネットワークの数学的な領域の一部とその基本的な定理の証明と簡略化について取り上げましたが、消費、交通、人口管理の世界における広範な応用が存在するため、理論を拡大し、フローネットワークのこれらの応用に関する知識を深めることは有益です。この目的のために、最も効率的なリソースは以下の通りです：

https://www.cs.upc.edu/~mjserna/docencia/grauA/P20/MaxFlow-fib.pdf

https://ocw.tudelft.nl/wp-content/uploads/Algoritmiek_Introduction_to_Network_Flow.pdf

We will continue to update VoAGI; if you have any questions or suggestions, please contact us!