ディリクレ分布:基本的な直感とPythonによる実装
Dirichlet Distribution Basic Intuition and Implementation in Python
ディリクレ分布について知っておくべきすべて
ディリクレ分布はベータ分布の一般化です。ベイズ統計学では、ディリクレ分布は多項分布の共役事前分布として一般的に使用されます。したがって、確率のランダムベクトルの不確実性をモデル化するために使用することができます。ベイズ解析、テキストマイニング、統計遺伝学、非パラメトリック推論など、幅広い応用があります。この記事では、ディリクレ分布の直感的な導入と多項分布との関連性を示します。さらに、Pythonでのモデリングと可視化方法も紹介します。
定義
X₁、X₂、…、Xₖ(k≥2)が連続的な確率変数であるとすると、ランダムベクトルXは次のように定義されます:
また、ベクトルαを次のように定義します:
ここで
ランダムベクトルXがパラメータαを持つディリクレ分布に従うとは、次の結合確率密度関数を持つことを意味します:
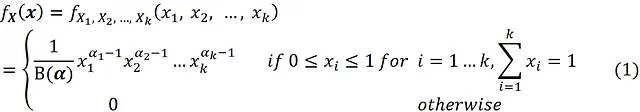
関数 B(α) は多変量ベータ関数と呼ばれ、次のように定義されます:
ここでΓ(x)はガンマ関数です。ランダムベクトルXがパラメータαを持つディリクレ分布に従う場合、X ~ Dir(α)と表記されます。多変量ベータ関数は、結合確率密度関数を正規化するために結合確率密度関数に含まれています。結合確率密度関数は、ドメイン全体で1に積分する必要があります:
したがって、次のようになります:
式1に基づいて、ランダム変数X₁、X₂、…、Xₖがfₓ(x)>0を満たすためには、以下の条件を満たす値を取る必要があります:
これらの条件は、ディリクレ分布のサポートを定義します。ランダムベクトルXおよびその分布のサポートは、fₓ(x)>0となるすべてのx(Xが取り得る値)の集合です。もしXがk個の要素を持つ場合、ディリクレ分布を持つXのサポートはk-1次元の単体です。単体は、式3の制約のために作成される有界線形多様体です。単体は、次元が高い場合でも三角形の概念を一般化したものです。したがって、k-1…
We will continue to update VoAGI; if you have any questions or suggestions, please contact us!
Was this article helpful?
93 out of 132 found this helpful
Related articles






